Структурная организация самоконтролируемых автоматов для систем реального времени

Информационно-управляющие системы (ИУС) реального времени составляют основу средств автоматизации для мехатроники, летательных аппаратов, навигационных комплексов, технологических процессов и др.

Наиболее распространенной структурной моделью ИУС является модель В. М. Глушкова в виде операционного устройства и управляющего автомата, осуществляющего выдачу комплекса микроопераций для управления операциями преобразования и обработки информации. Согласно модели В. М. Глушкова ИУС содержат только два равноправных блока: операционное устройство (ОУ) и управляющий автомат (УА) [1].

Более детальной является модель ИУС Ю. Ф. Мухопада в виде пяти взаимосвязанных блоков: функционального, информационного, адресного, логического и управляющего [2, 3]. Для простейших ИУС УА реализуется в виде микропрограммного автомата, для более сложных ИУС каждый из блоков модели рассматривается как соответствующая подсистема с собственным УА. При этом УА становится иерархическим: верхний уровень — программный, а нижний уровень — микропрограммный автомат (МПА). В ряде случаев верхний уровень УА реализуется как МПА со структурой Мура. В зависимости от типа ИУС нижний уровень УА может быть комплексом МПА Мура или Мили.

Актуальность проблемы . Из результатов анализа следует определяющая роль УА в обеспечении правильности функционирования ИУС. Кроме того, идеология автоматного управления исключительно важна в следующих приложениях:

• —    конечные автоматы являются основой управления в любых ИУС от бытовых приборов до автомобилей и сложных технических систем;

• —    развивается направление создания спецпроцессоров с таблично-алгоритмическим набором функциональных преобразователей и МПА [2–4];

• —    УА составляют основу построения сверхбыстродействующих аппаратных средств криптографической защиты информации [5, 6];

• —    развиваются ИУС с элементами искусственного интеллекта с УА в виде комплексного МПА и таблично-алгоритмические структуры с МПА для задач классификации и распознавания образов с использованием когерентных локаторов;

• —    автоматный подход внедряется в программирование как в UML-технологию, так и непосредственно для составления программ [7–10].

Как правило, ИУС предназначены для управления ответственными процессами, в которых недопустима выдача неправильных команд, создающих опасную ситуацию. Для таких ИУС используются УА со встроенными средствами контроля, способными выдать сигнал о неисправности УА в процессе работы до выдачи очередной команды управления. Такие УА называются самоконтролируемыми. Проектирование схем самоконтроля УА связано с проблемой проектирования надежных МПА, отличающихся минимальными затратами логических элементов. Поэтому необходимо рассматривать структурную организацию МПА и методы минимизации для определения встроенных средств самоконтроля.

Теория анализа и синтеза МПА создавалась в основном в 1960–1999 гг. В последующее десятилетие в основном происходила адаптация типовых структур МПА к элементной базе БИС и СБИС [8, 11]. Это позволило авторам работы [7] сделать вывод о том, что теория аппаратной реализации МПА полностью завершена и новые постановки следует ожидать лишь в вопросах программной реализации моделей МПА. В настоящее время очевидна ошибочность такого вывода, поскольку в ведущих научных школах России и за рубежом появились новые разработки в области анализа и синтеза МПА на БИС, а также продолжаются теоретические работы в области конечных автоматов.

Структурная организация автоматов управления . Необходимо провести анализ структурной организации МПА для определения наиболее уязвимых блоков с целью разработки встроенных средств контроля. На рис. 1 приведена типовая структура МПА с правилом функционирования автоматов Мура (ОУ — операционное устройство (объект управления), выполняющее для МПА роль логической подсистемы, так как в ее состав включены датчики и схемы формирования двоичных сигналов; { α } — входные сигналы МПА; И — регистры памяти, составляющие основу информационного блока МПА; А — комбинационная схема F 1 для определения кода Y = y m ••• у 2 у 1 состояния автомата a ( t + 1) по коду X = x m ••• x 2 x 1 состояния a ( t ) и логическим условиям а а 1 а 2 ••• a q ; F 1 — адресный блок МПА (наиболее простым методом реализации F ₁ является считывание кода Y по конкатенации а 1 а 2 • • • a q x m • • • x 2 x 1 , которая рассматривается как адрес ПЗУ); Ф — комбинационная схема F 2 для формирования управляющих команд A 1 A 2 • • • A k по коду состояния a ( t ); F 2 — функциональный блок; У — блок синхронизации (БС), формирующий по сигналу “Пуск” с периодом T импульсы синхронизации т 1 и т ₂ , причем т i ( t ) ^Л т 2 ( t ) = 0; БС — управляющий блок МПА). Число состояний автомата N определяет m — разрядность кодов X и Y в соотношении N <  2 m . При реализации адресного блока на ПЗУ или ПЛМ условный объем памяти равен V = m • 2 m ⁺ q .

При оценке сложности автоматов по сравнению с адресным блоком остальные блоки можно не учитывать. Действительно, логический блок Л не относится непосредственно к МПА, информационный блок И — это два m -разрядных регистра памяти с парафазной связью между ними, а управляющий блок У для МПА — одна типовая микросхема генератора

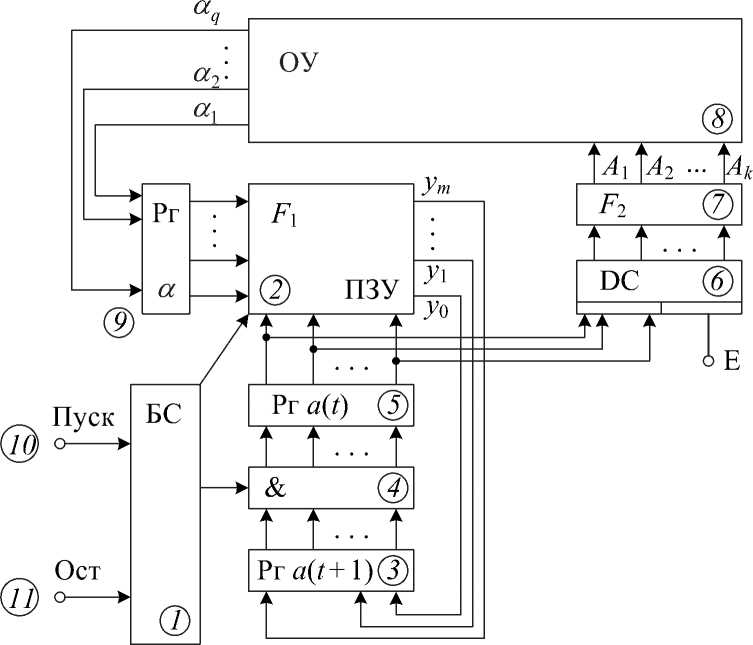
Рис. 1. Блок-схема автомата управления: 1–11 — номера блоков в порядке взаимодействия

Таблица 1

Основные параметры автоматов

Номер строки Тип m q m+q m+1 V W Q 1 CП 3 4 7 4 0,384 0,048 8 2 ПА 4 8 12 5 16 0,128 128 3 СА 5 12 17 6 640 0,320 2048 4 ВС 6 16 22 7 24 0,768 32 748 импульсов и RS -триггер для подключения синхросигналов. Поэтому сложность МПА определяется значениями m, q для всех блоков (Ф, И, Л, А) при фиксированной структуре БС классических МПА Мура.

По степени сложности адресного блока в соответствии с инженерной классификацией [9] МПА подразделяются на сверхпростые (СП), простые (ПА), средней сложности (СА) и высокой сложности (ВС) автоматы. В табл. 1 приведена оценка объема ПЗУ в килобитах. Из табл. 1 следует, что значение V для СА-автоматов может быть приближенно равно 1 Мбит, а для ВС составляет десятки мегабит.

При проектировании МПА прежде чем выбрать методы встроенного контроля, следует упростить А-подсистему. Существует два подхода:

Рис. 2. Блок-схема автомата управления с выбором логического условия: 1–15 — номера блоков в порядке взаимодействия; Ф — функциональная подсистема; И — информационная подсистема; Л — логическая подсистема;

А — адресная подсистема; У — управляющая подсистема

• —    минимизация системы m булевых функций F 1 и реализация их на ПЛМ или ПЛИС с конкатенацией входных переменных { а }{ x }; число переменных равно m + q ;

• —    представление системы F 1 параллельной последовательной структурой комбинационных схем (декомпозиция), в которой каждая из подсхем имеет число переменных на входе меньше m + q .

Первый подход эффективен для СП- и ПА-автоматов, но для СЛ- и ВС-автоматов снижение сложности А-блока не превышает 15 % [11–14]. Второй подход [11, 13, 15] отличается высокой наукоемкостью, так как при проектировании необходимо в графе переходов найти несовместимые подграфы, решить задачу оптимальной раскраски графов и т. д. Однако эффект для СЛ- и ВС-автоматов также незначительный [15–18].

В работах [14, 19] предложен эффективный метод декомпозиции МПА, основанный на разделении не графов переходов, а исходной граф-схемы алгоритма (ГСА). Метод позволяет снизить объем ПЗУ (ПЛМ) в 1,5–1,7 раза для ВС- и СЛ-автоматов.

В работах [9, 20, 21] предложен кардинальный подход к снижению сложности А-блока, основанный на использовании оригинальной структуры МПА (рис. 2) с определением Y по коду X при использовании только одного логического условия a j Е { а } . Номер j для a j определяется по коду a ( t ). Метод синтеза таких МПА Мура и Мили приведен в работах [2, 9, 14]. Объем ПЗУ такого А-блока определяется величиной W = m • 2 ^{m +1} . Значение W не зависит от числа логических условий q . Выигрыш в объеме ПЗУ, обозначенный символом Q , и величины W для всех типов автоматов приведены в табл. 1. Для СЛ- и ВС-автоматов выигрыш составляет от единиц до десятков тысяч раз.

Вносимые в новую структуру МПА новые блоки в виде мультиплексора для выбора a j E { а } и комбинационной схемы F 3 для определения j по коду a ( t ) в сумме не превышают сложности новой комбинационной схемы F 1 c m + 1 переменной на входе.

В начальный период развития теории МПА различали автоматы Мура, Мили и В. М. Глушкова. Однако затем автоматы В. М. Глушкова не стали выделять как самостоятельные, так как они имеют обобщенную структурную организацию без конкретизации способов формирования выходных сигналов.

Структурная схема МПА с выделенным мультиплексором не только оригинальна, но и отлична от типовых структур Мура и Мили. Поэтому новая структурная организация МПА определяет также принципиально новый подход к синтезу высоконадежных МПА и организации для них встроенных средств самоконтроля.

Методы контроля и диагностики МПА. Достаточно полного обзора методов контроля МПА не проводилось, поэтому в данной работе рассмотрены основные из них. В 1970– 1980-х гг. появились работы, посвященные контролю и диагностике ЭВМ, в которых частично ставилась задача контроля устройств управления, главным образом в режиме тестовой (предстартовой) проверки МПА [22–24]. Динамический контроль конечных автоматов развивался самостоятельно в двух не строго разделимых направлениях:

• —    встраивание средств контроля в уже спроектированный МПА;

• —    проектирование МПА, обладающих свойством самоконтроля.

Одной из первых появилась работа А. Д. Закревского [22], в которой предложена минимизация систем булевых функций не только основных разрядов, но и дополнительных, образующих контрольные биты, соответствующие коду Хэмминга [23]. Метод обеспечивает высокий уровень контролеспособности при небольшом увеличении объема F ₁ , однако не нашел применения вследствие необходимости встраивать в структуру МПА сложный декодер кода Хэмминга.

Корректирующие коды, используемые для контроля комбинационных схем МПА, подробно рассмотрены в ряде монографий [24–27], а эффективность метода для обеспечения надежности МПА оценена в работе [28].

Второй подход предложен М. А. Гавриловым [29] для синтеза d -безотказных автоматов, правильно выполняющих функции при числе отказов t <  d . Для реализации метода необходимо:

• —    представить состояния МПА векторами (словами) минимально избыточного корректирующего кода;

• —    чтобы расстояние между отдельными векторами соответствовало кодовому расстоянию по Хеммингу не менее 2 d + 1.

Метод М. А. Гаврилова изложен в работе [24], однако он также не нашел применения вследствие необходимости введения значительной избыточности и без того сложных СА- и ВС-автоматов.

В большинстве методов динамического контроля используются специальные коды для представления a ( t ) и a ( t + 1) вместо двоично-позиционного (ДПК) или двоичного соседнего кода (кода Грея). Поэтому далее следует рассмотреть различные типы кодирования для обеспечения самоконтроля МПА.

В работе [30] предложено использовать код с фиксированным числом “1”, обозначенный kCn, т. е. k единиц в n-разрядном коде. Этот метод имеет несколько модификаций, в частности разделение m-разрядного кода a (t) на две части и представление каждой из них кодом kCn, например 2 из 5 или 3 из 7 [16]. В работе [17] изложены методы синтеза схем проверки наличия двух единиц в пятиразрядном коде или трех единиц в семиразрядном коде и др. В работе [31] предложена модификация метода kCn, позволяющая обнаруживать отказы разрядных переходов из “0” в “1”.

Метод контроля kCn является наиболее простым и быстродействующим, но сами комбинационные схемы определения k единиц в n -разрядном результате достаточно сложны. Кроме того, объем ПЗУ равен не V = m • 2 ^m + q , а V = 2 m • 2 ^{2 m} + q .

Предлагается также при кодировании a ( t ) в виде ДПК дописать инверсный код, соответствующий числу единиц в ДПК (коды Бергера). Этот метод требует выполнения операций подсчета числа “1” в ДПК и сравнения с инверсным кодом [17, 24].

Другим подходом к контролю является метод В. Н. Балакина и В. В. Барашенкова [32, 33], который требует введения в структуру МПА счетчиков для определения числа операторов перед проверкой логических условий, введения в граф переходов специальных контролирующих состояний и др. Метод эффективен, так как не только проверяет правильность переходов a ( t ) ^ a ( t + 1), но и обнаруживает неверную генерацию A i вместо A j . Такие средства контроля весьма сложны, но применимы для контроля параллельных процессов [34].

Результативным подходом является метод А. Н. Буинова [35], предложившего построить объединенную матричную модель сигналов, представленных множеством допустимых состояний (матрица A ) и множеством запрещенных состояний для каждого допустимого состояния a ( t ) (матрица B ). Сравнение входных сигналов при достигнутом состоянии a ( t + 1) с матрицами A и B позволяет принять решение о правильности функционирования МПА. Метод А. Н. Буинова требует очень больших аппаратных и временных затрат и не нашел применения для динамического контроля, однако может быть использован для тестового контроля МПА, который в данной работе не рассматривается.

При динамическом контроле применим также известный метод полного дублирования МПА. Вариантом более эффективного контроля является самодвойственное дублирование, обеспечивающее в среднем 67 % избыточности при 99 % покрытия неисправностей [36]. Однако этот метод требует дальнейшего исследования, так как одновременно требуется двойная временная избыточность.

Новые методы самоконтроля. В работе [37] с целью уменьшения числа активных элементов в числовом блоке ПЗУ предложено использовать представление хранимого кода с фиксированным числом единиц как результат независимой дешифрации частей m -разрядного кода ДПК. Код назван геометрическим, так как работа [37] опубликована до появления кодов kCn . Более подробно метод изложен в работе [3]. В работе [38] идея этого метода использована для контроля ПЗУ. Для контроля МПА использован модифицированный геометрический код (МГК), определенный в виде конкатенации трехразрядных групп с одной единицей в каждой, причем в общем коде (МГК) с разрядностью n = 2 m ( m — разрядность ДПК) недопустимо соседство двух единиц в соседних разрядах между группами. Оригинальность метода [39] контроля МПА с МГК определяется тем, что код МГК используется только для представления a ( t + 1). Код a ( t + 1) по цепи обратной связи преобразуется в модифицированный двоичный код (МДК) по правилу 001 ^ 00 , 010 ^ 01 , 100 ^ 10. Тогда на входе F 1 в коде a ( t ) в каждой группе из двух разрядов не должно быть комбинации “11”, а на выходе F 1 в каждой группе из трех разрядов допустима единственная комбинация с одной “1”.

По уровню контролеспособности предложенный метод эквивалентен методу kCn, однако схемы определения наличия одной “1” в каждой группе из трех разрядов тривиальны в реализации, в отличие от схем определения k произвольно расположенных “1” в n-разрядном коде. Для МГК ошибка (ERR) в каждой группе из трех разрядов, обозначенных побитно a, b, c, определяется выражением

ERR = abCc + abc + abc).

Предложенный оригинальный метод самоконтроля [39] наиболее эффективен для новой структуры МПА, так как при использовании ПЗУ объем памяти W = т - 2 m +1 станет равным W = (2 т + 1) • 2 m +2 ( т + 1 — разрядность МДК; 2 т — разрядность МГК). Для типового МПА Мура при использовании МГК и МДК объем памяти равен W = 2 т • 2 2 m + q .

Для новой организации МПА становятся эффективными также другие методы контроля, в частности метод мажоритарного дублирования схемы F 1 . Применительно к МПА этот метод модифицирован следующим образом. Используются три комбинационные схемы F 1 , однако две из них осуществляют прямое преобразование a ( t + 1) = F i ( a j a ( t )), а третья схема реализует обратное преобразование a ( t ) = F 10 ( a j a ( t + 1)), причем в дублированных F 1 используется МГК, а в F 10 применяется МДК для представления a ( t + 1). Алгоритм проверки включает следующие действия:

• 1.    Проверка отсутствия ошибок в МГК для всех дублированных F 1 , обозначенных F ₁ ¹ и F 1 ² . Если в каждой схеме ошибки отсутствуют, то при равенстве выходов F 1 ¹ и F 1 ² код a ( t +1) считается верным.

• 2.    При наличии ошибки в одной из дублированных схем выполняются преобразование a ( t ) = F 10 ( a j a ( t + 1)) и сравнение полученного кода a ( t ) 0 с исходным кодом a ( t ). При равенстве кодов результат считывается с исправной схемы F 1 . Иначе фиксируется ошибка.

Предложенный метод контроля обеспечивает безопасный режим работы МПА при любой кратности ошибок в А-подсистеме. Очевидно, что такой метод контроля невозможен в МПА с классической структурой Мура, так как в таких автоматах невозможно построить F ₁ ¹ , F ₁ ² , F ₁ ⁰ .

В новой структуре МПА применим еще один вариант дублирования комбинационной схемы F ₁ . Структура МПА определяется следующими модификациями:

• —    в графе переходов МПА выделяется наиболее длинный путь, удовлетворяющий условию a ( t + 1) = 1+ к a ( t ) ( к — признак безразличного выбора значения к );

• —    для этих переходов предусматривается счетчик с кодом Грея, который одновременно выполняет роль выходного регистра памяти a ( t + 1) в И-системе МПА;

• —    остальные переходы реализуются схемой F ₁ ;

• —    параллельно устанавливается дублирующая схема для вычисления кода a ( t +1). В этой схеме F ₁ ¹ используется принцип независимого вычисления первой Y 1 и второй Y 2 половин Y кода a ( t + 1) по первой X 1 и второй X 2 частям X кода a ( t ) с учетом a j для первой и второй частей.

Поскольку при X 1 и X 2 используются только части X единого кода x 1 x 2 ··· x m , при вычислении Y 1 и Y 2 возможно появление неопределенности. Для ее ликвидации используется еще одна двоичная переменная γ , значение которой определяется в основной схеме F 1 совместно с кодом Y = у 1 у 2 • • • y m .

В предложенной схеме вычисления Y дублированная схема определения кода a ( t + 1) требует меньших затрат, чем при полном дублировании F 1 .

Синтез встроенных средств контроля рассмотрим на примере МПА с т = 4, q = 6, алгоритм работы которого представлен в виде логической схемы алгоритма (ЛСА)

2       1       2       13         3         45              5               64

A ₀ ↓ A ₁ α ₁ ↑ A ₂ α ₂ ↑ A ₃ A ₄ ↓ ↓ A ₅ A ₆ α ₃ ↑ A ₇ A ₈ α ₄ ↑ ↓ A ₉ A ₁₀ A ₁₁ α ₅ ↑ A ₁₂ A ₁₃ A ₁₄ α ₆ ↑ ↓ A ₁₅ A _k .

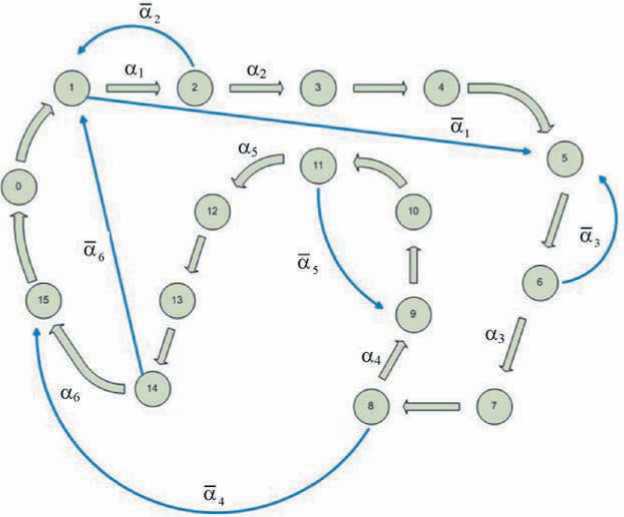
Рис. 3. Граф переходов МПА:

0-15 — узлы графа, соответствующие состояниям МПА; а 1 ,..., а 6 , а",..., а 6 — условные связи

В работе [2] приведены правила перехода от ГСА к ЛСА. Представленная ЛСА получена после модификации ГСА за счет введения пустого оператора A 2 . Граф переходов МПА для ЛСА представлен на рис. 3 (двойными стрелками отмечен непрерывный путь через состояния 0 , 1 , 2 ,..., 15 , 0). Такому пути может быть поставлен в соответствие счетчик, работающий в коде Грея (табл. 2). В этом случае схема F ₁ реализует только шесть переходов по табл. 3. Заметим, что все переходы в F 1 реализуются по условию ∝ j , так как по условию ∝ j для данного примера переходы осуществляются по счетчику. Для построения контролирующей схемы по табл. 3 строится табл. 4, в которой в первом столбце введена логическая переменная y для снятия неопределенности при некоторых кодах: x 1 x 2 (00 ^ 01 , 00) и x з x 4 (01 ^ 01 , 11). Булевы функции у 1 , y 2 , у 3 , у 4 определяются по картам Карно на основе табл. 4. Реализация этих функций тривиальна, так как для примера определяется уравнениями

У 1 = ( x 1 x 2 + Yx 2 ) « ,

• У 2 = ( Yx 1 x 2 ) « ,

• У 3 = Y ( x 4 + x 3 ) « ,

у 4 = Yx 3 x 4 ^ -

При реализации МПА Мура по традиционной схеме с дублированием F 1 при m = 4 , q = 6 общий объем двух схем составит более 8 кб, так как для каждой схемы W = m • 2 ^m+^q . В новом автомате необходимы одна схема с объемом W = m • 2 ^{m +1} = 0,127 кб и тривиальная дублирующая схема для реализации уравнений Y . При больших значениях m, q преимущество предлагаемого метода самоконтроля и новой структуры МПА будут еще более значимыми.

Таблица 2 Четырехразрядный код Грея				Таблица 3 Функции переходов МПА
Номер	0000	8	1100	a ( t )	α	a ( t +1)
1	0001	9	1101	1	∝ 1	5
2	0011	10	1111	2	∝ 2	1
3	0010	11	1110	6	∝ 2	5
4	0110	12	1010	8	∝ 4	15
5	0111	13	1011	11	∝ 5	9
6	0101	14	1001	14	∝ 6	1
7	0100	15	1000

Таблица 4

Кодирование функций переходов МПА

γ	N ( t )	α	N ( t + 1)
0	0001	0	0111
1	0011	0	0001
0	0101	0	0111
0	1100	0	1000
0	1110	0	1101
1	1001	0	0001
γ	X 4 x 3 x 2 x 1	α	Y 4 y 3 y 2 y 1

Предложенные методы синтеза безопасных МПА применимы в ИУС, не использующих параллельные процессы вычисления и управления. Параллелизм проявляется лишь в наборе микроопераций C ₁ C ₂ ··· C _k в командах A _i ∈ { A } . При параллельных вычислениях и одновременной выдаче нескольких команд управления перспективен подход с применением сетей Петри. В работе [40], по-видимому, впервые для контроля ИУС применены сети Петри с запрещающими дугами. Позднее такие модели были названы joiner-сети [41, 42].

В работах [14, 40] показано, что сеть Петри с запрещающими дугами реализуется двумя взаимодействующими автоматами, для которых входы одного автомата являются выходами другого.

При системном анализе методов и средств динамического контроля МПА рассмотрены лишь основные принципиально различающиеся постановки. Полный детальный анализ работ, посвященных построению безопасных автоматов, будет упрощен за счет использования результатов анализа, выполненного в данной работе.

Следует отметить особую роль исследований научной школы В. В. Сапожникова и Вл. В. Сапожникова. Результаты их многолетней деятельности приведены в фундаментальной публикации [43].

Следует отметить также высокую значимость новой структурной организации МПА для повышения контролеспособности и надежности.

В представленной работе в основном рассматривались автоматы Мура. Метод построения МПА Мили с новой структурной организацией предложен в работе [44].

Исследования новой структурной организации МПА только начаты, поэтому имеется резерв как для модификации, так и для создания новых методов самоконтроля МПА.

Заключение . Предложенная в данной работе структурная организация микропрограммных автоматов предоставляет возможность построения высоконадежных систем управления с оригинальными средствами самоконтроля, обеспечивающими режимы безопасной работы сложных технических систем реального времени при минимальных затратах специально встраиваемого оборудования.