Структурная устойчивость спиральных пучков и тонкая структура потока энергии

Впервые структуры сингулярных пучков в виде упорядоченных комбинаций оптических вихрей, способных принимать форму отдельных геометрических фигур, букв и даже слов, были представлены еще в 1996 г. и названы спиральными пучками [1]. Они относятся к структурированным пучкам (tailoring beams [2]), которые являются объектом исследования сингулярной оптики на протяжении последних 30 лет [3– 8]. Спиральные пучки находят применение в задачах создания энергетически эффективных дифракционных оптических элементов [9], манипуляций микрочастицами [10] и микроскопии сверхвысокого разрешения [11]. Особый интерес вызывает свойство спиральных пучков формировать ограниченные волновые структуры типа узлов и петель из света [12], а не из структурированной темноты [13].

Спиральные пучки являются решениями параксиального волнового уравнения [14, 15], а эволюция их energy flow. Computer Optics 2021; 45(4): 482- поперечного распределения интенсивности при распространении в свободном пространстве выглядит как поворот:

• .    z 1   / Г „.

I (r, ф, z) =  ----- Il ---- Ф+0 arctg z ,0 I,(1)

1 + z2 ( V1 + z2

где r, φ и z – цилиндрические координаты, продольная координата z измеряется в единицах длины Рэлея zR, т.е. z→z / zR , а радиальная координата r нормирована на радиус перетяжки w0 Гауссова пучка, т.е. r → r / w0. Параметр вращения θ задаёт полный угол поворота θπ /2 интенсивности от плоскости перетяжки до Фурье-плоскости, причём это вращение замедляется с ростом z. (Следует отметить, что в непараксиальном варианте возможно равномерное вращение интенсивности светового поля [16].) Траектории оптических вихрей в спиральном пучке лежат на поверхности однополостного гиперболоида вращения. При |9| = 1 траектории оптических вихрей являются прямыми линиями, а при |9| > 1 оптические вихри двигаются в пространстве по спиральным линиям [15]. Спиральные пучки также являются структурно устойчивыми волновыми конструкциями с точностью до линейных масштабных преобразований. Чтобы подтвердить это, необходимо внимательно вглядеться в скрытую тонкую волновую структуру пучка. Такую возможность дают как прямой эксперимент, так и теоретический анализ критических точек потока энергии.

Целью нашей статьи является детальный теоретический и экспериментальный анализ быстровращаю-щихся скалярных спиральных пучков с параметрами вращения 9 = - 1 и 9 -- 3, а также анализ критических точек потоков энергии. Пучки с такими значениями параметров имеют относительно простое математическое представление, что значительно упрощает их описание и понимание физических процессов, протекающих при их распространении.

Базисные и симметричные спиральные пучки

Известно [15], что если параметр вращения является нечётным отрицательным числом, θ = -2 N -1, то условие (1) позволяет записать спиральный пучок в виде разложения по вполне определённому набору ортонормированных мод Лагерра–Гаусса (ЛГ):

F - 2N - i ( r , z ) - S A n , n f n LG Nn , n ( r , z ). (2)

n > 0

Здесь и далее значение параметра вращения θ будет указываться как нижний индекс F , r - ( r cosф, r sinф),

LGp,t (r, z) - Cp,t x f2-o)p 1 f r2VreiфY ., f2r2 x ---- ~exP----- Lp ,

I o J o I o A o J   (|o| J стандартные нормированные ЛГ- моды, p и t - радиальный и азимутальный индексы (нас интересует только случай t > 0), о - 1 + iz - вспомогательный комплексный параметр, используемый для краткости,

„ _ \2    2 '/ !

С и / — I--- p '   \л ( p + / )!

нормировочные коэффициенты. Коэффициенты разложения пучка F –2 N –1 ( r , z ) записаны в виде произведения двух множителей. Первый множитель, A N , n , зависит от параметра вращения. Для рассматриваемых в данной статье случаев N =0 и N = 1

Nn

A N.n ^{- 2}

n !

( Nn )! —

2 2 ⁿ ( Nn + n )!

.

Второй множитель, f n , не зависит от N и определяет форму распределения интенсивности спирального пучка.

Благодаря условию сохранения интенсивности (1) при распространении спирального пучка, мы можем рассматривать комплексную амплитуду пучка только в плоскости перетяжки, z - 0, и не записывать z среди аргументов:

-- 2 N - 1 ( r ) - S A n , n f n LG Nn , n ( r ).

n > 0

(2 ' )

Простейшим спиральным пучком для случая

N - 0 является смещённый Гауссов пучок с линейной фазой,

F _{- 1} ( r | c ) - exp( - r ² + 2 c * re i ^ф - cc * ) -- S A , n f n ( c )LG 0, n ( r ), n > 0

где fn ( c ) - exp ( - cc *)(2 c *) n / n ! и c - комплексный параметр, определяющий величину и направление смещения (звёздочка означает комплексное сопряжение). При N >0 спиральным пучком, родственным (3), является смещённый псевдогауссов пучок,

F - 2 n - 1 ( r | c ) - S A n , n f n ( c )LG Nn , n ( r ),                (4)

n > 0

который имеет форму циклоидальной замкнутой линии [15].

Если спиральный пучок обладает радиальной симметрией, его ЛГ- представление (2 ' ) можно упростить, исключая нулевые члены. Например, для суперпозиции трёх псевдогауссовых пучков, смещённых в вершины правильного треугольника с центром на оптической оси, { c 1 - iR , c ₂ - iRe ^2п i ^/3, c ₃ - iRe ^-2п i ^/3}, получаем f_3n ( л , R ) - exp( - R ²)( - 2 iR )^{3 n} / (3 n )! и нулевые коэффициенты f 3 n +1 и f 3 n +2 . В результате спиральный пучок принимает вид

F - 2 n - 1 ( r Л , R ) - S A n ,3 n f 3 n ( л , R )LG 3 Nn ,3 n ( r ).       (5)

n > 0

Подобным свойством обладают и коэффициенты спирального пучка в форме плоской кривой. Известно [14], что для 9 -- 1 комплексная амплитуда спирального пучка, поперечное распределение интенсивности которого локализовано вблизи плоской кривой, имеет форму

F-1 (r|^(t), t е [0,T]) = exp(-r2)x xITexp{2^‘(t)rei^   2|t)I2 + 4iS(t)}l^(t)dt■      ( )

Здесь ζ ( t ) – комплексное параметрическое представление кривой на плоскости, ζ′( t ) – её производная и

4S(t) - 2j0Im{^‘ (t)C'(t)}dт - учетверённая площадь сектора, заметаемого радиус-вектором r, соединяющим начало координат с точкой ζ(t), при движении вдоль кривой.

Чтобы получить представление пучка (6) в виде разложения по ЛГ- модам, запишем экспоненциальный множитель, содержащий re^{i φ}, в виде ряда Тейлора и воспользуемся определением ЛГ- моды:

exp ( - r ² + 2 Z * ( t ) re » ) - e - r ² E {2 ^ * ⁽ t ) re i ' } n - n > 0          n !

- E ^ ( t ^)} n A , n LG o, n ( r ). n > 0       n !

Как следствие, пучок (6) принимает вид

F - i ( r | Z ( t ), t e [0, T ] ) - E A . n f n №». n ( r )

n > 0

f n ( Z ) - | n -[ T exp { —|Z ( t )|² + 4 iS ( t ) } Z * ⁿ ( t ) |Z' ( t )| dt.

Если кривая ζ( t ) замкнута (контур), то поперечное распределение интенсивности пучка (8) имеет форму кривой только в том случае, если площадь внутри контура, S ( T ), удовлетворяет условию квантования :

4 S ( T) - 2n j , j - 1, 2,.... (9)

Например, для окружности, Z( t ) = О ( t )= Re i , T - 2п, из условия квантования, 4n R ² - 2п j , находим радиус. Окружность принимает вид О j ( t ) - ^ j(I e" , соответствующий спиральный пучок оказывается ЛГ-модой, F _-1( r | О j ) - LG₀ , j ( r ), поскольку только один коэффициент отличен от нуля: f_n ( О j ) -5 _n , j . Один ненулевой коэффициент позволяет легко записать и общий случай: F _-2 N _—1(r| О j ) - LG Nj,■ ( r ), опуская несущественный постоянный множитель A Nj , j .

Рассмотрим теперь спиральный пучок для случая, когда замкнутая кривая Z( t ), t e [0,2п], обладает радиальной симметрией, т.е. для некоторого целого M выполняется условие Z( t + 2п / M) - Z( t ) e ²ⁿ i / ^M . Если кривая удовлетворяет условию квантования, 4 S (2п) - 2п j , то коэффициенты f n (ζ) отличны от нуля только тогда, когда ( n – j )/ M является целым числом. Кроме того,

симметрия пучка приводит к симметричному расположению оптических вихрей. Все оптические вихри, за исключением находящегося в центре (если он там есть), расположены в вершинах одного или нескольких правильных M -угольников.

Рассмотрим, например, кривую в форме границы правильного треугольника: r ( t ) = iRe^it (2+(1/2) e ^{–3 it} ), t e [0, 2п]. Тогда M = 3. Величину R находим из условия квантования: R - ^ j /7 . Пусть для простоты j - 7. Тогда для спирального пучка F _—1 ( r | Д7) только коэффициенты f 1 , f 4 , f 7 , … отличны от нуля. Упрощая

(8) и отбрасывая несущественный постоянный мно-

житель, который входит во все f n , мы получаем

F - 2 N - 1

^{( r 1 r}7 ) ^- E A N ,3 n + 1

n > 0

f 3 n + 1 ^(r7^)LG N (3 n + 1),3 n + 1

( r ),

(—i )3 n+1 2T fin+i(r?)  ---------[ exp(—2cost — |isint)x

^J3 n ^V7V (3 n +1)! [    ^{P(           3       )}         (11)

x e (2 n ) t (4 + e i ) 3 n ⁺ 1 5 — 4 cos t dt .

Пучок (10) имеет 7 оптических вихрей внутри контура Д7: один на оси пучка и шесть - в вершинах двух правильных треугольников.

Тонкая структура оптических токов

Фазовая функция комбинации вихревых пучков даёт исчерпывающую информацию об их скрытых свойствах, в частности, об их структурной устойчивости не только относительно пространственного и углового сдвига, но также их отклика потоков энергии на различные внешние возмущения. Берри тщательно проанализировал структурированную ткань потоков вектора Пойнтинга в сложных векторных полях и назвал их оптическими токами (или линиями тока) [17]. Он подчеркнул, что оптические токи не следует путать с оптическими лучами в геометрической оптике: лучи света распространяются в однородной среде по прямой, в то время как оптические токи могут вычерчивать порой весьма причудливые траектории в окрестности критических точек. Также Берри обнаружил [18], что критические точки в потоке разделяются на два типа сингулярностей: оптические вихри, в окрестности которых линии тока близки к окружностям, и седла, где линии тока асимптотически близки к гиперболам. Заметим, что замысловатая картина оптических токов характерна не только для оптических процессов, а имеет топологическую природу и является неотъемлемой частью потоков воздуха и жидкости в аэро- и гидродинамике [19]. Возникает вопрос, могут ли особенности структуры особых точек указать на причины устойчивости (или неустойчивости) сложных спиральных пучков?

В качестве примера рассмотрим спиральный пучок треугольной формы F _-1 ( r | Д₇), получающийся из (10) при N - 0. Линии тока направлены вдоль локального волнового вектора k и описываются вектором оптического тока J в виде [17]

J - Im{ F *( r ) d x F ( r ), F *( r ) d y F ( r )}, (12) т.е. вектором, пропорциональным усреднённому по времени вектору Пойнтинга (см. также [20]).

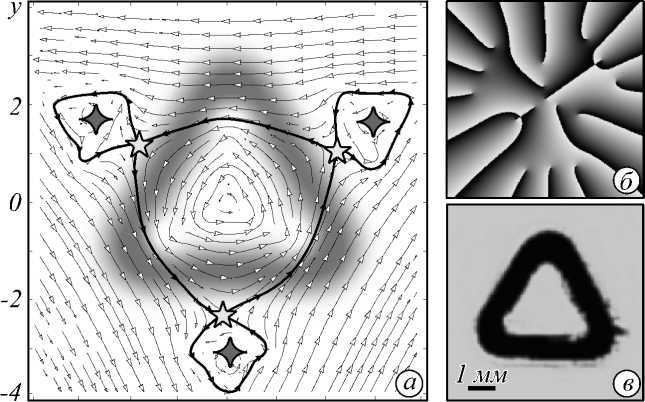
Компьютерное моделирование картины линий тока, рассчитанное на основе формул (10)–(12), представлено на рис. 1. Здесь, наряду с вполне ожидаемым течением линий тока, появляются совершенно новые черты. Так, типичное поведение линий тока в окрестности оптических вихрей на рис. 1 а сочетается с неожиданным масштабным эффектом (характерным для фрактальных структур [19]), когда крупный узор критических точек повторяется в мелких элементах картины. Сетка сепаратрис разделяет линии тока на несколько характерных участков (рис.1 д – ж ). Каждый участок содержит четверку критических точек с аналогичным узором линий тока, что и в центральной области. Но если главный центральный участок, содержащий три устойчивые критические точки типа

центр, охватывает симметричная сепаратриса, проходящая через три седла, то сепаратрисы внешние более мелких участков проходят только через одно седло и слегка деформированы. Представленная геометрия критических точек построена таким образом, что внешний поток вытесняется к центру, а внутренний поток наоборот – на периферию. В результате формируется правильный треугольник интенсивности света, который можно рассматривать как аналог каустики [21]. Так как спиральный пучок F _-1 ( r | Д 7 ) соответствует случаю N = 0 в (10), мы можем изменить направление течения линий тока на противоположное простым переключением знака топологического заряда во всех модах спирального пучка.

-4      -2       0       2 х

-0,4     0     0,4 х -4,5-4,0-3,5-3,0-2,5 х

-1,0 -0,5 0 0,5 х 2,0 2,5 3,0 3,5 4,0 х

Рис. 1. Спиральный пучок F -i ( r | △ ? ): (а) линии тока на фоне распределения интенсивности, (б) распределение фазы, (в) интенсивность (эксперимент) для z = 0, линии тока во внутренней (г) и внешней (д-ж) области треугольника. Критические точки двух типов – центр и седло ; среди других линий сепаратриса выделяется толщиной

Теперь рассмотрим математический формализм описания линий тока для общего случая N> 0 спиральных пучков в базисе ЛГ-мод. При дифференцировании полиномов Лагерра воспользуемся формулой (1.22.1.3) из [22]: dXL(x) = -L“+1(x) . Тогда d xF (r) = -2 xF (r) + U (r) - 4 xV (r), dy F (r) = -2 yF (r) + iU (r) - 4 yV (r), где

U ( r ) = exp( - r ² ) £ f n n ( x + iy ) n ^{- 1} L N (2 r ²), n > 1

V ( r ) = exp( - r ² ) ^ f n ( x + iy ) ⁿ L N - 1 (2 r ²) n > 1

(для случая N = 0 функция V ( r ) тождественно равна нулю), и мы приходим к общему выражению для поперечной проекции линий тока спиральных пучков

J = ( Im{ F * (U - 4 xV ), F * ( iU - 4 yV )} ) .         (15)

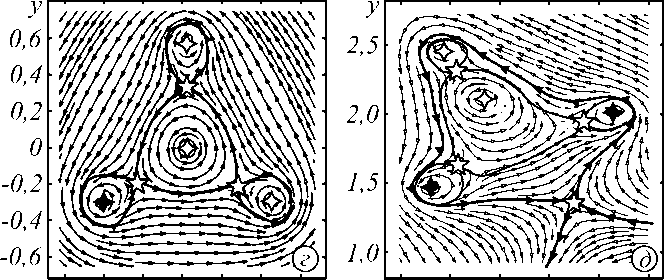
Линии тока на рис. 2 иллюстрируют устойчивую сингулярную структуру смещённого Гауссова пучка в исходной плоскости z = 0. Группа оптических вихрей (справа от центра) задаёт сложный узор критических точек. Почти вся центральная темная область пучка на рис. 2 а , плотно покрытая сетью связанных между собой «зубчатых» фазовых сингулярностей (рис. 2 б ), смещает яркое световое пятно на периферию.

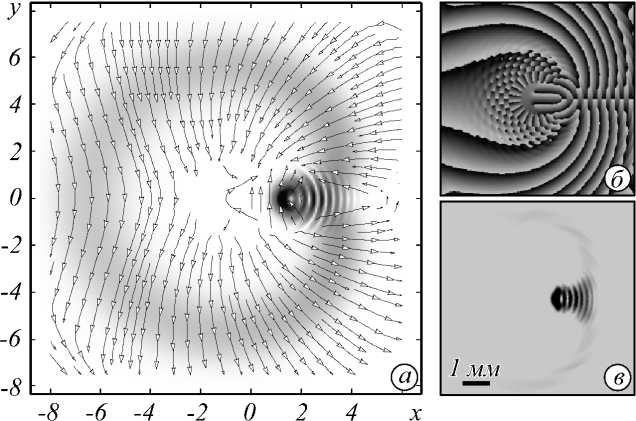
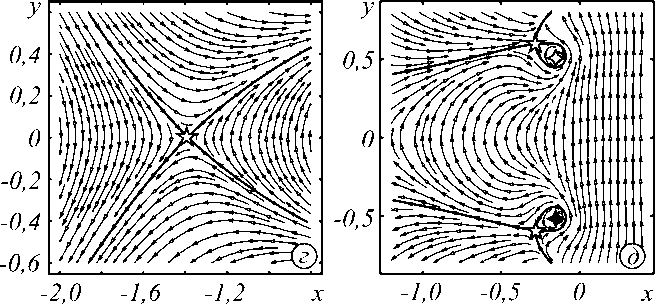
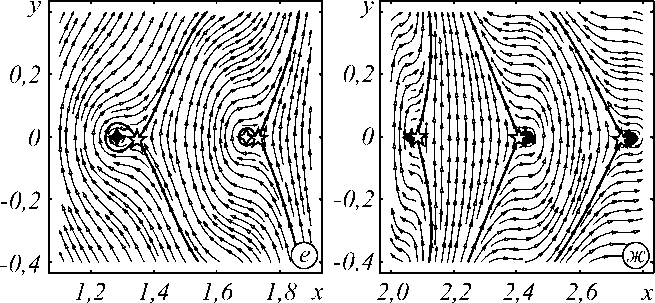
Рис. 2. Псевдогауссов пучок F - з ( г 1с = 1,8): (а) линии тока на фоне распределения интенсивности, (б) фаза спирального пучка, (в) интенсивность (эксперимент) для z = 0, (г - ж) картины линий тока в отдельных фрагментах вдоль оси абсцисс. Критические точки те же, что и на рис. 1

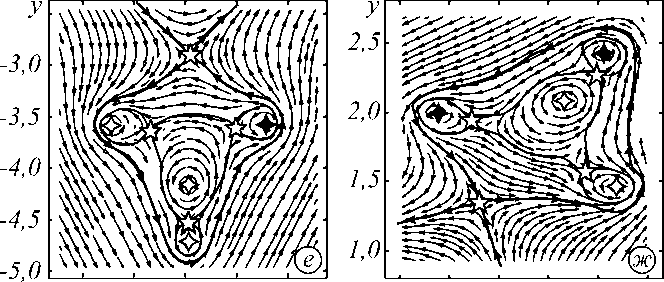
Именно такой смещенный пучок и служит основой для построения сложных спиральных пучков (см. рис. 3). При распространении вдоль оси z вся картина линий тока поворачивается на угол 3π /2. В наших численных экспериментах мы использовали формулы (4) и (5), заменяя ряды конечными суммами с 0 <  n <  30 и 0 <  n <  6 соответственно.

-б -4   -2    0    2    4 х

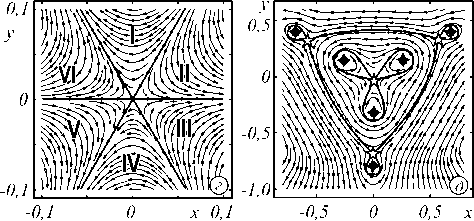
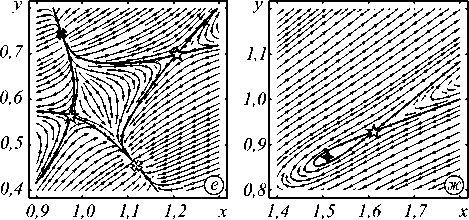
Рис. 3. Спиральный пучокF -3 ( r | .^-.,R = 1,6): (а) линии тока на фоне распределения интенсивности, (б) фаза спирального пучка, (в) интенсивность (эксперимент) для z = 0, (г-ж) картины линий тока в отдельных фрагментах первого квадранта. Кроме критических точек типа «центр» и «седло», появляются устойчивый узел и неустойчивый узел

Эксперимент

Экспериментальное решение проблемы пространственной эволюции спиральных пучков затрагивает два аспекта измерений. Волновая функция спиральных пучков содержит множество ЛГ- мод высших порядков с различными радиальными и азимутальными числами, поэтому SLM-модулятор и детекторы должны иметь достаточно большую разрешающую способность. Кроме того, полученные результаты должны позволить рассчитать орбитальный угловой момент (ОУМ), информационную энтропию (меру беспорядка, возникающую при распространении), то- пологический заряд и возможность осуществлять соответствующую коррекцию возмущенного пучка.

Разрешающую способность экспериментальной установки мы оценим позже, а сейчас укажем, что всеми необходимыми требованиями к процессу измерений обладает метод моментов интенсивностей, подробно описанный в недавних статьях [23, 24].

Эскиз экспериментальной установки представлен на рис. 4. Гауссов пучок от He-Ne лазера (Thorlabs HNL100RB, X = 0,6328 цт) после пространственного фильтра L1 –L2, отражаясь от SLM-модулятора (Thorlabs EXULUS-4K1/M), превращался в спиральный пучок. Далее делительная призма BS расщепляла пучок на два оптических плеча. В первом плече спиральный пучок посредством сферической линзы L3 ( f = 15 см) проецировался на входное окно металл– оксид–полупроводникового детектора CMOS1 (Michrome 20). Детектор закреплялся на оптическом столике, снабженном 3D-микровинтами, осуществляющим продольный сдвиг с точностью 0,1 мм в области фокусировки пучка. После цифровой обработки данных вычислялись моменты интенсивности и спектр мод Лагерра–Гаусса (или Эрмита–Гаусса), которые выводились на экран монитора. Аналогичные операции осуществлялись во втором оптическом плече, где на входное окно CMOS2 детектора спиральный пучок проецировался с помощью цилиндрической линзы CL ( f' = 30 см). Эти дополнительные измерения позволяют измерять фазы мод в случае, когда в пучке содержатся ЛГ- моды как с положительным, так и c отрицательным топологическим зарядом. Разрешающая способность экспериментальной установки задается CMOS-детектором и SLM-модулятором с размером каждой ячейки порядка 4 ц т. Такая разрешающая способность позволяет воспроизводить и детектировать пучки, содержащие более 150 ЛГ мод (см. также [25]).

Спектры мод для различных типов спиральных пучков иллюстрирует рис. 5. Результаты эксперимента немного отличаются от предсказаний теории, но не более чем на 6%, и попадают в интервал ошибки эксперимента. В реальном эксперименте мы измеряем как обычные, так и нормированные спектры амплитуд, что позволяет не только сравнивать с теорией, но также рассчитывать ОУМ, топологический заряд и другие параметры пучка.

Особое внимание мы уделили исследованию эволюции спиральных пучков высших порядков вдоль оси распространения z , которая позволяет оценить некоторые аспекты структурной устойчивости.

Наша экспериментальная установка может регистрировать картину интенсивности вдоль пучка в окрестности фокуса с точностью до 0,5 мм и рассчитывать преобразования линий тока и положения критических точек. Но при подготовке эксперимента особое внимание следует уделить качеству голографических решеток на рабочем элементе SLM- модулятора (см. рис. 6). Если пучки не обладают осевой симметрией, то их интенсивность неравномерно распределена по площади голографической решетки. Поэтому важно аккуратно центрировать пучок на голограмме. Кроме того, дополнительное вращение передают локальные изгибы интерференционных полос на месте кольцевых дислокаций на рис. 6б, г. Всё это требует тонкой подстройки как направления лазерного излучения, падающего на голограмму, так и SLM-модулятора с помощью микровинтов.

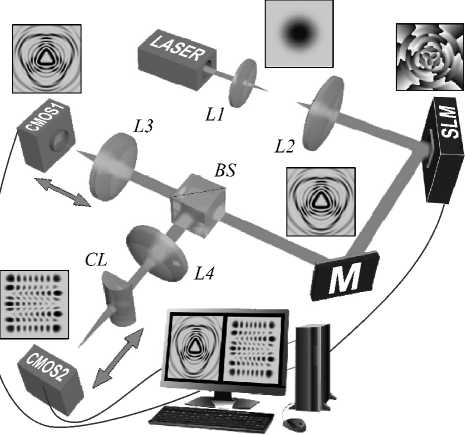
Рис. 4. Схема экспериментальной установки.

LASER – He-Ne лазер, SLM – пространственный модулятор света, L1-L4 – сферические линзы, CL – цилиндрическая линза, BS – делительная призма, CMOS1, CMOS2 – детекторы, M – зеркало

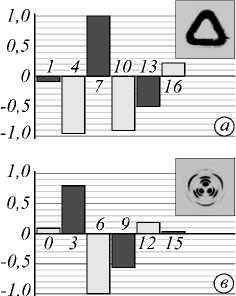
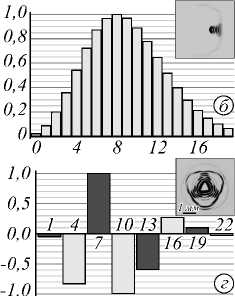
Рис. 5. Коэффициенты разложения A N,n f n спиральных пучков по базису ЛГ- мод в зависимости от n:

(а) треугольный пучок F -i ( r | Д?), (б) смещённый псевдогауссов пучок F -3 ( r | с = 0,5), (в) комбинация трёх смещённых псевдогауссовых пучков F -s ( r | л ,К = 1,6), (г) треугольный пучок F -s ( r | Д 7 ). Все коэффициенты вещественны или чисто мнимы (соответствующие столбцы закрашены светлым или тёмным цветом) и отмасштабированы по модулю максимума. В правом верхнем углу каждого кадра показано экспериментально зарегистрированное распределение интенсивности для z = 0

Картины интенсивности на рис. 6 приведены для триплета смещённых псевдогауссовых пучков, F _-3( r | л , R =1,6), и пучка F _-3( г | Д₇). Более простая форма триплета псевдогауссовых пучков практически не разрушается при вращении (рис. 7 а ), но более сложная структура треугольного пучка (рис. 7 б ) испытывает искажения треугольного обрамления в виде появления спиральных рукавов в области длины Рэлея ( z = 1) при сохранении формы центральной части пучка. Конечно, такое искажение можно объяснить неточностями юстировки оптической системы. Однако подобная частичная потеря структурной устойчивости при продольных смещениях характерна для сложных волновых конструкций. Поэтому прежде чем перейти к детальному исследованию проблемы структурной устойчивости, мы решили дать простое феноменологическое объяснение этому процессу.

а)

а)

в)

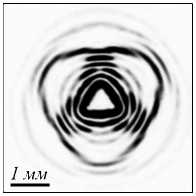
Рис. 6. Экспериментальные распределения интенсивности для z = 0 (а,в) и дифракционные решетки (б,г) для пучков

б)

г)

F -3 ( r | /. ,R = 1,6) и F -3 ( r | Д 7 )

б)

Рис. 7. Эволюция быстро вращающихся спиральных пучков при распространении вдоль оси z (мм), угол поворота распределения интенсивности обозначен а :

(а) F -3 ( r \ л ,К = 1,6) и (б) F -3 ( r | Д 7 )

Хорошо известно [26], что ЛГ- пучки с комплексным аргументом быстро теряют свою исходную форму при распространении. Обобщенная форма ЛГ-пучков, зависящая от параметра a , который может быть комплексным, была предложена в работе [27]:

gLG p_{> t} ( r , z | a ) = C p_{> t} ( a ) x

p

I 1 — a о I x| I

( (1 — a ) o J

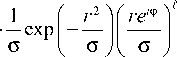
t

Lp

r ²

о (1 — a о )

(при a = 1 /2 получаются стандартные ЛГ- моды).

Наш предварительный анализ показал, что использование таких ЛГ- пучков в формуле (2) дает появление спиральных рукавов в пучке F _-3 ( г | Д₇), при этом сохраняя внутренний треугольник. Поэтому мы предложили модель, осуществив в (2) замену

LG p, t ( r , z ) ^ gLG p, t ( r , z H2 + e )

(очевидно, что ряд (2) после такой замены удовлетворяет параксиальному уравнению). Для построения было выбрано значение e = 0,04, при котором эксперимент хорошо согласуется с моделью (см. рис. 8). В области длины Рэлея ( z =60 мм) возникает разрушение треугольного обрамления, которое развивается, образуя три спиральных рукава. Однако феноменологическая модель не связывает параметр e с конкретными возмущениями пучка на эксперименте, но только намечает направление дальнейших исследований проблемы структурной устойчивости спиральных пучков.

интенсивности (б) с теоретической моделью (а), £= 0,04

Заключение

Мы показали, что структура спиральных пучков поддерживается комплексным распределением потоков с характерным расположением пар точек «центр – седло» и триад «стабильный узел – седло – нестабильный узел», связанных сетью сепаратрис, что определяет характерную форму пучка. Численные эксперименты показали, что огибающие линий потока треугольных спиральных пучков также имеют треугольную форму, что доказывает каустическую природу максимумов интенсивности спиральных пучков. Мы экспериментально зафиксировали вращение при распространении спиральных пучков с разными параметрами поворота, но в тексте мы зафиксировали только поведение наиболее характерных пучков: линейную композицию трёх псевдогаус-совых пучков и треугольного пучка. Мы обнаружили, что критические точки суммы трёх псевдогауссовых пучков следуют за распределением интенсивности и сохраняют их структурную устойчивость при распро- странении. Абсолютно другой сценарий реализуется для треугольных пучков. Если при распространении пучка на расстояние длины Рэлея форма пучка сохраняется, то при дальнейшем распространении внешний треугольник разрушается и превращается в спираль, тогда как внутренний треугольник поворачивается на угол 3π /2 без потери формы.

Мы рассмотрели простую теоретическую модель устойчивости формы пучка, добавляя небольшое возмущение в полином Лагерра. Численное моделирование показало хорошее согласие между теорией и экспериментом. Мы считаем, что небольшие отклонения от формы комплексной амплитуды спиральных пучков объясняются погрешностями при реализации голографической решётки SLM- модулятора. Однако это предположение требует более глубокого теоретического и экспериментального исследования.

Работа выполнена при поддержке РФФИ и Совета министров Республики Крым (проекты № 20-47910002 в части «Теоретические результаты», № 2037-90066, № 19-29-01233 в части «Методы измерения спектра оптических вихрей», № 20-37-90068 в части «Экспериментальные результаты»).