Структурно-физическая модель спутникового радиоканала с учетом поглощения и сцинтилляций волны в ионосфере

Известно [1-4], что возмущения ионосферы, сопровождаемые образованием интенсивных мелкомасштабных неоднородностей (ММН) электронной концентрации (ЭК), обуславливают возникновение сцинтилляций (то есть амплитудно-фазовых флуктуаций, замираний) волны на входе приемника (ПРМ) систем спутниковой связи (ССС). Это вызывает существенное снижение их помехоустойчивости. Зачастую одновременно с образованием ММН возрастает и среднее (фоновое) значение ЭК ионосферы. Это обуславливает дополнительное поглощения волны в ионосфере и, как следствие, снижение мощности принимаемого сигнала и помехоустойчивости ССС [5-8].

Чтобы спрогнозировать влияние сцинтилляций и поглощения волны в ионосфере на помехоустойчивость ССС, необходимо разработать структурно-физическую модель трансионосферного канала связи (КС) с целью установления зависимости передаточной функции КС (определяющей мощность принимаемого сигнала) от физических параметров неоднородной ионосферы (среднего значения ЭК и их флуктуаций в ММН).

Также известен [4; 9] общий подход к построению структурно-физической модели трансионосферного КС. Он базируется на комплексном применении методов, разработанных в статистической теории связи (построения многолучевых моделей КС с замираниями) и статистической радиофизике (методы фазового экрана, параболического уравнения) для описания одного и того же процесса распространения радиоволн (РРВ) через неоднородную ионосферу в радиолинии «Искусственный спутник Земли (ИСЗ) – Земля». Отождествление полученных данными методами результатов позволило найти зависимости статистических характеристик (СХ) передаточных функций трансионосферного КС с замираниями (сцинтилляциями) от флуктуаций ЭК в ММН ионосферы и несущей частоты передаваемого сигнала. В частности, установлены зависимости регулярной и флуктуационной составляющих коэффициента передачи трансионосферного КС по мощности от несущей частоты передаваемого сигнала, среднего значения ЭК на высоте максимума ионизации и интенсивности ММН ионосферы на этой высоте PkN = P^N Ц^н ) •

Первым недостатком полученных в [4; 9] результатов является то, что функциональная зависимость позволяет оценить влияние на коэффициент передачи трансионосферного КС таких физических параметров ионосферы которые трудно определить с помощью традиционных средств ионосферного мониторинга: например, вертикального зондирования [10]. В настоящее время наиболее совершенными являются средства GPS-мониторинга ионосферы, то есть пассивного мониторинга ионосферы с использованием двухчастотного приемника спутниковых радионавигационных систем (СРНС) GPS/ГЛОНАСС [11-12]. Они позволяют определить полное электронное содержание (ПЭС) ионосферы и его статистические характеристики: среднее значение и среднеквадратическое отклонение (СКО) мелкомасштабных флуктуаций [13]. Однако ранее они не использовались для построения структурно-физической модели трансионосферного КС.

Вторым недостатком известного подхода [4; 9] является то, что он не учитывает дополнительные потери при распространении радиоволн из-за поглощения (ослабления) в возмущенной ионосфере. Считается, что при использовании в ССС несущих частот поглощением в ионосфере можно пренебречь [5-6]. Однако при использовании в ССС пониженных несущих частот (до и частот диапазона используемых низкоорбитальными ССС (типа ORBCOMM, Го-нец-Д1М и др.), увеличение среднего значения ПЭС ионосферы при ее возмущениях может приводить к существенному уменьшению мощности принимаемого сигнала из-за поглощения волны в ионосфере, характеризуемого множителем , где – среднее значение эффективной частоты соударений электронов (ЭЧСЭ). Вследствие этого составляющие коэффициента передачи трансионосферного КС по мощности должны зависеть как от СКО мелкомасштабных флуктуаций ПЭС ионосферы, так и от его среднего значения          и среднего значения ЭЧСЭ:

К ’²⁽⁷« } = Н-Л ’ °№_т ,N_T,v₃\

Целью настоящей статьи является разработка методики установления зависимости регулярной и флуктуационной составляющих коэффициента передачи трансионосферного КС по мощности от несущей частоты передаваемого сигнала ССС, значений СКО мелкомасштабных флуктуаций полного электронного содержания ионосферы     (определяющих проявление ее сцинтилляционных свойств), а также средних значений полного электронного содержания и эффективной частоты соударений электронов в ионосфере (определяющих проявление ее поглощающих свойств).

Для достижения поставленной цели необходимо сначала разработать модель изменения электронной концентрации в неоднородной ионосфере с учетом указанных параметров ионосферы               Затем на основе модели ионосферы разработать математическую модель трансионосферного канала связи с учетом поглощения и сцинтилляций, которая позволит найти зависимость составляющих коэффициента передачи этого канала связи          от несущей частоты сигнала и указанных параметров ионосферы ^\NT ’■^Т’^э )•

Модель пространственного изменения электронной концентрации в неоднородной ионосфере

Согласно [4; 14-15], изменение ЭК в слоях ионосферы            с мелкомасштабными неоднородностями (см. рисунок 1а) описывается совокупностью изменения по высоте ее среднего значения и пространственных флуктуаций

N( p,z)=N(z)+^N(.p,z) = = ^z)^l +Д^(p,z)/^(z)^

На рисунке 1 б показано изменение по высоте ЭЧСЭ в слоях             ионосферы.

Связь между высотным изменением ЭК ионосферы и ее ПЭС (или интегральной ЭК) при распространении радиоволн через всю ее толщину определяется полным количеством электронов в столбе сечением 1 м ² вдоль пути распространения [15]:

В соответствии с (1) ПЭС неоднородной ионосферы будет описываться совокупностью среднего значения и пространственных флуктуаций :

N_T^p^= ^N^p,z^dz = J^(z) + ^(/?,z)](/z =

= pV(z)Jz + ^^N^p,z^dz = N_T + ^N_T^py

Качественный анализ (3) и рисунка 1 а позволяет сделать вы в од о том, что среднее значение ПЭС ионосферы определяется в основном средней ЭК на высоте максимума и ониз а ции в слое ионосферы:                       .

В этом случае выражение для в (3) можно представить в виде формулы для площади прямоугольника (см. заштрихованную область на рисунке 1а), эквивалентной площади под кривой [15]:

N_r = pV(z)<7z = ^(z_m)t/z =

= Z3N(zm) = z3Nm , то есть в виде однородного по высоте слоя с эквивалентной толщиной и средней ЭК, равной

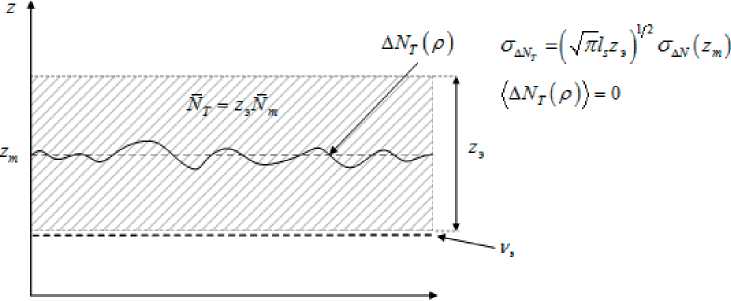
Проявление сцинтилляционных свойств ионосферы определяется пространственными флуктуациями ПЭС в ММН ионосферы Z^dV_T(p^= JaA^/^z^z .

Чтобы установить связь статистических характеристик мелкомасштабных флуктуаций ПЭС ионосферы с флуктуациями ее ЭК , необходимо второе слагаемое в (3) записать в следующем виде [9]:

Z\Nr^p^= jzdV(p,z)dz =

= jAjV(p,z = zm)dz,

имеющем физический смысл флуктуаций ПЭС в слое (см. рисунок 2) с эквивалентной толщиной и ЭК, равной со статистически однородно размещенными внутри него неоднородностями с флуктуациями ЭК, соответствующими высоте максимума ионизации

Связь СКО флуктуаций ЭК на высоте               максимума ионизации

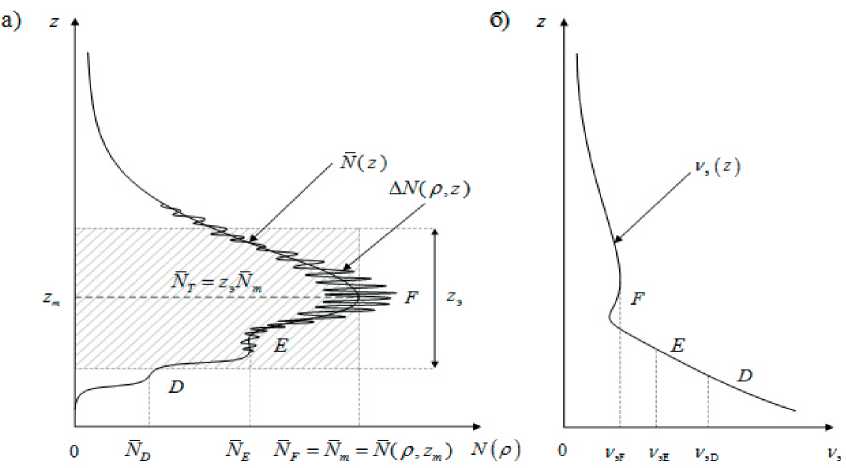
Рисунок 1. Изменение по высоте электронной концентрации ионосферы с мелкомасштабными неоднородностями и эффективной частоты соударения электронов

с величиной

СКО ПЭС получена в виде [4]:

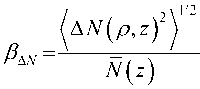
^SN (Z)

ZAIN \ m /              ,

~ const,

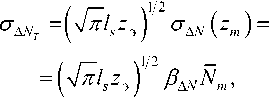
где интенсивность мелкомасштабных неоднородностей

характеризует отношение СКО ф л уктуаций ЭК ^AV(^Zj к ее среднему значению ^(д) ’ которое практически не зависит от высоты 2 (см. рисунок 1 а ).

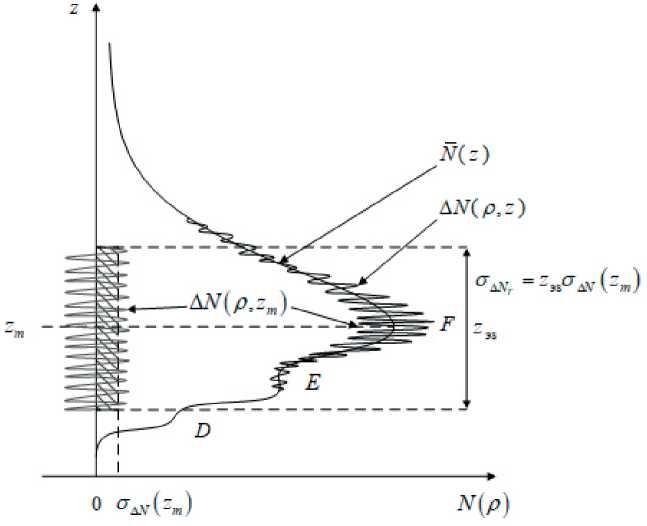
Рисунок 2. Изменение по высоте электронной концентрации ионосферы с мелкомасштабными неоднородностями и флуктуации ее полного электронного содержания

Анализ выражения (6) показывает, что сомножитель (V^/^)' = -« можно рассматривать как эквивалентную толщину тонкого ("эл «->) ионосферного слоя с расположенными внутри него статистически однородно по пространству кр’²^ неоднородностями ЭК ^р^, соответствующими высоте т максимума ионизации слоя F ионосферы. Эти неоднородности характеризуются нулевым математическим ожиданием (a^(az„,)) = O и постоянным СКО ^UJ^^^ Данный тонкий слой полностью определяет мелкомасштабные флуктуации ПЭС ионосферы ^т(рУ характеризующиеся нулевым средним значением (&N_T(p)} = 0 и постоянным СКО (6) ^ам₇ =(V4^Z₃) 0_№N_m =z_3S&N(zJ .

Для учета поглощения энергии волны при распространении в ионосфере необходимо дополнительно учесть результаты, полученные в [7-8]. Согласно [6], коэффициент поглощения мощности волны в ионосфере (^_п²) зависит от интегрального произведения изменений по высоте z среднего значения ЭК ионосферы N (zj и ЭЧСЭ v₃ (z), показанных на рисунках 1 а и 1 б :

W^ = exp

-2,7-lO"³/^² jw(z)v₃(z)^

О

<1. (8)

Качественный анализ рисунков 1 а и 1 б показывает, что основной вклад в результирующее значение интегрального произведения JjV(z)v₃ (z)<7z вносит слой F ионосферы, поскольку ЭК на его высот а х намного выше, чем в нижних слоях D и E-. N_F « N(z_m)» N_E » N_D .

Это подтверждается данными, приведенными в [7-8], согласно которым интегральное произве- дение ЭК и ЭЧСЭ в слое F лишь немного меньше, чем во всей ионосфере. На основании этого, а также предположения о том, что основной вклад в ПЭС ионосферы (4) вносит слой F , выражение (8) можно представить в виде [8]

где ^ал – угол РРВ через ионосферу; y₃=v_9F-^v_3F=2,78-10³ [с"¹] – среднее значение ЭЧСЭ в ионосфере, отличающееся от значения v_3F=2.10³[c-'] ЭЧСЭ в слое F на величину поправочного коэффициента Jv_3F -1,39. Это обусловлено тем, что ЭЧСЭ в слое F меньше, чем в нижних слоях ионосферы ^F < ^эЕ < ^D (см. рисунок 1б).

На основании изложенного комплексную модель распределения ЭК неоднородной ионосферы по высоте z и пространству P = k^XP’^ можно представить в виде (см. рисунок 3) совокупности трех слоев:

– однородного слоя с эквивалентной толщиной Z₃ , расположенного на высоте z=z_m максимума ионизации и характеризующегося средним значением ПЭС (4) N_T=FN_m;

– расположенного на его нижней границе тонкого слоя, где происходят столкновения электронов с ионами и ней т ральными молекулами с эффективной частотой v₃;

– тонкого слоя неоднородностей, расположенного на высоте m максимума ионизации, который описывается статистическими характеристиками пространственных флуктуаций ПЭС NN_T^_Py. нулев ым математическим ожиданием ^NN_T(p)^ = G и постоянным СКО (6) ^NN_T =№и=У ' P_№N_m =Z_3SCr_Mm^ .

P

Рисунок 3. Комплексная модель ионосферы в виде совокупности толстого однородного слоя электронной концентрации, тонкого слоя ее неоднородностей и тонкого слоя, в котором происходят соударения электронов

Достоинством данной модели является использование для ее описания параметров неоднородной ионосферы Nj и ^ю , которые можно определить методом пассивного мониторинга с помощью двухчастотного приемника СРНС без трудоемких предварительных расчетов эквивалентной толщины ионосферы z₃, среднего значения максимальной ЭК N_m , характерного (среднего) размера мелкомасштабных неоднородностей к , СКО флуктуаций ЭК ионосферы на высоте максимума ионизац ии ^KN (^Zm ) и интенсивности неоднородностей Av^v^j/a^zJ .

Кроме того, она точнее отражает физический смысл известного [1] утверждения , что о сновной вклад в среднее значение ПЭС kN_T-N^ и его флуктуации ^M^ ~ ^KN (^Zm ) ) вносит ЭК ионосферы в слое F на высоте максимума ионизации ^Zm ^.

Математическая модель трансионосферного канала связи с учетом поглощения и сцинтилляций волны

Проанализируем процесс распространения радиоволн при передаче комплексного сигнала

$t (0 = A exp(ytiv) - ^ exp[j (rtV + Ф,)] (10)

с частотой ®₀ = ²^A, мощностью P, и начальной фазой Ф, при вертикальном (a_T=90 ) РРВ

(см. рисунок 4) от ИСЗ (то есть передатчика (ПРД) ССС) до ПРМ ССС через неоднородную ионосферу, описываемую комплексной моделью распределения ЭК (см. рисунок 3). Здесь S,=J^ и ^=^ехр(₇'Ф_?) – амплитуда и комплексная амплитуда передаваемого сигнала соответственно. Распространение волны происходит в пределах области пространства (p\ ограниченной первой зоной Френеля.

В соответствии с рисунком 4 методика разработки математической модели трансионосферного канала связи с учетом поглощения и многолучевого распространения должна в общем случае включать следующие этапы:

– определение комплексного поля u(t,z₀) плоской волны на некотором расстоянии z₀ от ИСЗ, соответствующем верхней границе ионосферы;

– определение поля волны »(^z’^z™) в плоскости тонкого неоднородного слоя (фазового экрана, расположенного на высоте ^z = ^z„, t соответствующей расстоянию z_o+O,5z₃ от ИСЗ);

– определение поля волны i(^t,z = z₀ +^_э) на нижней границе ионосферы (на расстоянии ^Z0^+Z3 от ИСЗ) с учетом поглощения ( ^n )’

– определение поля волны z/(?,z) на входе приемной антенны (на расстоянии Z = z_o + z₃ + Z[ от ИСЗ);

– определение комплексного сигнала v co на входе ПРМ ССС;

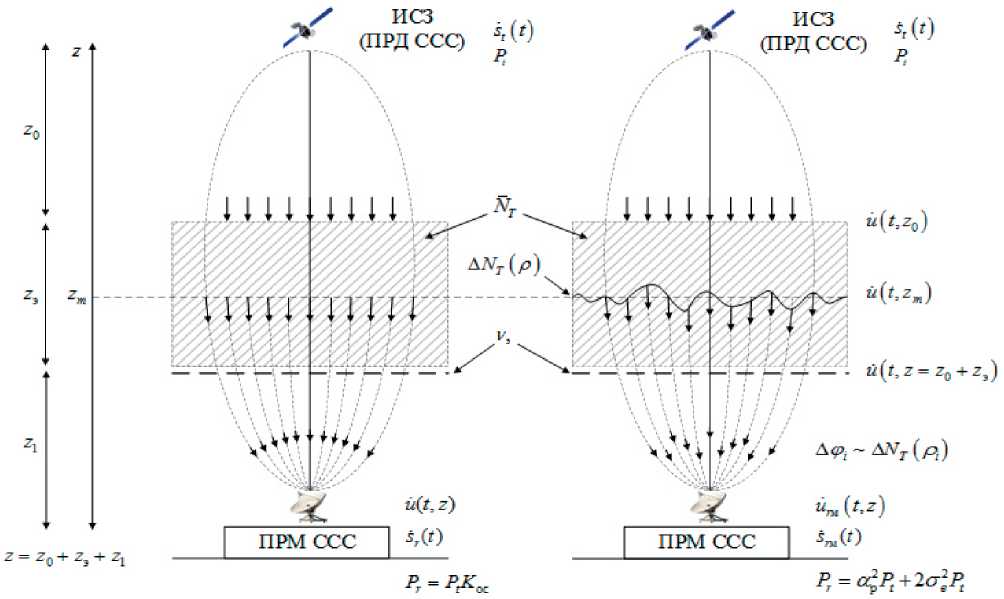
Рисунок 4. Процесс распространения радиоволн через ионосферу

– определение мощности сигнала Р₍ на входе ПРМ ССС.

В самом простом случае РРВ через однородную ионосферу (см. рисунок 4 а ), когда флуктуации ПЭС отсутствуют ^N_т(p) = Q, все участки плоского амплитудно-фазового фронта волны в пределах первой зоны Френеля приходят в точку размещения приемной антенны практически синфазно. При этом комплексное поле плоской волны на входе приемной антенны будет описываться выражением [4; 9]:

ДА z) = A(z) exp {/ [(to,/ + Ф_г) - ^(z)] } =

=V^vx ^exp U [^/+^фх - P(~)]} •

Здесь А^ = _Х\Р,КД^ – амплитуда во фронте волны; KSz^^G^/^W^²^ – коэффициент ослабления мощности 1РД излучаемой волны длиной Л)^{— c}/ .fo с учетом коэффициента усиления G_t и КПД Ht передающей антенны ИСЗ на расстоянии z в свободном про-странстве, Wyk^kM²^ и из-за поглощения в ионосфере, который определяется согласно (9) при cr, = 0 как

^² = exp (-2,7 • 1 O’³ v.N_T / /₀²)

Фазовый фронт волны, приходящий на вход приемной антенны, описывается выражением фк2^ = Фо (z) + ^(z)= (oazlc + 80,8л"NT/cf0 , (12)

где z) ^{= cu}o^z/^c – набег фазы в свободном пространстве на расстоянии z, причем ^(z) = ф = 80,8л" N_T /cf. – запаздывание фазового фронта волны с частот о й /о в ионосфере со средним значением ПЭС N j-.

В соответствии с выражением (11) комплексный сигнал на выходе приемной антенны (на входе ПРМ ССС) описывается выражением sAt^uAtV.^^P.K^z^x хехр[/[(су/+ Ф;)-<р][ =       (13)

= ^P_tK_0C exp{/[(to/ + O,)-^]}.

Здесь Z_ru= (^/4^)7^760 – постоянный сомножитель нормированной функции раскрыва приемной антенны с коэффициентом усиления G_r и КПД *lr ’ а коэффициент ослабления мощности передаваемого сигнала (7^) на входе ПРМ определяется как

Кос = K_ k²K = G_tn_tG_rnX (^z)^n = K>² Л14)

где К» = G_tr]_tG_rriX (- ) = GtntG,n,. {c/^zf₀ )² – коэффициент ослабления мощности сигнала при вертикальном РРВ в свободном пространстве.

Тогда мощность принимаемого сигнала P_r в трансионосферном КС при вертикальным РРВ (a_T =90°) с учетом множителя поглощения волны в ионосфере (9) описывается выражением

P_r = |i,. (Z)|² = P,K_0C = P_tKX = P.G_tn_tG_rn_r x X (с/4лг /_о )² exp (-2,7 • 10"³ v₃N_T /fo ).

Проанализируем случай вертикального распространения передаваемого сигнала (10) через неоднородную ионосферу с учетом проявления не только поглощения, но и сцинтилляций (см. рисунок 4 б ).

В этом случае необходимо учитывать наличие флуктуаций ПЭС в ионосфере AN_Tkp)>0, то есть тонкого слоя неоднородностей, расположенного на высоте ^ ^m максимума ионизации. Наличие такого слоя (называемого фазовым экраном) обуславливает появление искажений в фазовом фронте волны:

Vk³™^ = % k^Zm ) ⁺ Vk^Zm ) ⁺ M^m^P^ " (16)

Третье слагаемое в (16) характеризует флуктуации (искажения) фазового фронта волны в горизонтальной плоскости P = V^X'^ на выходе тонкого неоднородного слоя ионосферы ^² = ²„Л относительно среднего значения Фк²т\ которые обусловлены флуктуациями ПЭС ионосферы AN_Tkp> и определяются согласно [4; 9] как

Mkz_m,p) = ^7rZ^_Tkp>J^ (17)

В соответствии с (16) комплексное поле волны на выходе тонкого неоднородного слоя ионосферы U = Zm) описывается выражением йkt’Zm,P^^^PДД2^X

Выражение (18) можно записать в виде й ^,zm,p^ukt,zm )exp[-/AVkzm,p)] , (19)

где и O’^z™) = ^KJ²,,,) exp {7 k_W + Ф,) - Ф k²„,)]} - комплексное поле плоской волны при распространении в однородном ионосферном слое, а сомножитель exp[-7'A^(^z„,,p)] характеризует флуктуации (искажения) фазового фронта выходной волны (17), определяемые флуктуациями ПЭС ионосферы A^^).

Дальнейшее РРВ за ионосферным слоем до точки размещения приемной антенны М^М можно представить в виде множества (z = l ... M) элементарных лучей, образуемых элементарными участками YwY = Pi на поверхности фронта волны на выходе неоднородного ионосферного слоя ( - = -m )•

В соответствии с (19), комплексное поле элементарной волны (луча), образованной элементарным участком Pi на поверхности фазового экрана, описывается выражением

w(^ 2_m,_Pi^ u^t,z_m )exp \-jN(p^z_m,_Pi )] . (20)

Поскольку РРВ от тонкого неоднородного слоя ионосферы (Z = ZJ до точки приема

Очевидно, что относительные отклонения фазы в различных участках фронта волны на выходе ионосферы (17) определяют относительные фазовые сдвиги приходящих лучей MXhPYMMu поэтому выражение (21) можно записать в виде

u(t,z,_Pi) = й (/, z) exp \-j^ф_i ] = й ^t,zy_iH , (22)

где e,„ =exp[-yA^(z,

/?,.)] = exp [(-/Apz)] =

– комплексный нормированный коэффициент передачи трансионосферного КС по i -му лучу.

Поскольку на вход приемной антенны приходит не один, а множество (z=lM) элементарных лучей (волн), то поле принимаемой волны в трансионосферном КС с многолучевостью можно описать суммой элементарных полей:

^й™ и, ^z)=E ⁱ'*^’^z’ р^⁼^ “ (^z’^z) ^exp H м,)=

M                         (24)

= й^,2^в^=й^,2^в,.

где

M M eH = ^e/H ^exp(-yA^;) = м                                 (25)

= S ^CXP ^”j ⁸⁰’^8ЯА^ ^P> )/^C^0 )

– нормированное значение комплексного коэффициента передачи трансионосферного КС c многолучевостью, обусловленной мелкомасштабными флуктуациями ПЭС ионосферы ^T^PiY’ uY^V^O^Wt, комплексное поле принимаемой волны в трансионосферном КС с учетом поглощения в ионосфере при отсутствии многолучевости, определяемое согласно (11).

Полученное выражение (24) для комплексного поля многолучевой волны на входе приемной антенны «гм (0 позволяет определить аналогично (13) комплексный сигнал на выходе приемной антенны (на входе приемника ССС) в виде

SrM^MUmY^Y¹,» =V^oc ^X

M                  (26)

Здесь sAtVK_oe~w_a – комплексный сигнал на входе ПРМ с учетом поглощения без многолучевости определяется согласно (13) и (14), а влияние многолучевости учитывается нормированным коэффициентом передачи e_H, определяемым согласно (25).

В соответствии с (26) мощность принимаемого сигнала в многолучевом трансионосферном КС определяется как p™ = Km (0|2 = к (Фн|2 = PtK0C |®н Г =

= pA^\2=prC=PtGtntG,.nX^XX,

где ^р,=^р,К_ж – мощность принимаемого сигнала в трансионосферном КС с учетом поглощения волны ^п ) – определяется согласно (15), а квадрат модуля нормированного коэффициента передачи трансионосферного многолучевого КС kl²-< по своему физическому смыслу соответствует множителю ослабления мощности принимаемого сигнала из-за сцинтилляций (^:ц ) при распространении волны через ионосферу с ММН ЭК.

В соответствии с (25) этот множитель сцинтилляций принимаемого сигнала связан с флуктуациями ПЭС в ММН ионосферы как

^сц =|ё„|² = ^ехр(-уА^) = ^^ехР (“> 80, %ttNN_t (р, )/с/₀)

Поскольку множитель сцинтилляций принимаемого сигнала ^СЦ является случайной величиной, то обычно в мно г олучевых КС определяют среднюю мощность Р т сигнала на входе ПРМ (27), которая в общем случае содержит регулярную Рр и флуктуационную составляющие [16]:

^. =44.44^ 4ФЛ4 = = Л4+2Л4 =4 + 4|l,- где «р =^oc|«J2 и 2< =/4ек – регулярная и флуктуационная составляющие коэффициента передачи КС.

Обычно эти составляющие определяются экспериментально и вклады в их значения факторов многолучевости и поглощения не разделяются. Кроме того, в рамках методов построения многолучевых моделей трансион ос ферного КС получить из выраже ни я (28) для ^гп аналитическую зависимость < = Л^//о) множителя ионосферных сцинтилляций от СКО мелкомасштабных флуктуаций ПЭС ионосферы ( ^ДХг ) и выбора несущей частоты в ССС (/о) невозможно. Для решения этой задачи необходимо использовать методы статистической радиофизики.

Полученное выражение (24) для комплексного поля волны на входе приемной антенны «гм (О позволяет также получить выражение для средней интенсивности /,. (z) поля принимаемой волны. В общем виде оно определяется как

I,\z^M

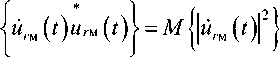
где х и М {х} – обозначения математического ожидания х, а х – комплексно-сопряженная функция X. Тогда подстановка в это выражение (24) с учетом (11) дает

4 (4= ^р,к_ж ^м к _вн = P_tK_0C (z)M^_H I²} =

=ptM4

В рамках статистической радиофизики регулярная Ip и флуктуационная ^фл составляющие средней интенсивности (4-4 ^{+ /}фл) поля волны в точке приема (>o = 0,z) при трансионосферном РРВ определяются методом фазового экрана согласно выражениям [4; 9; 17]:

^р (z) = ^0 (^)ехр(-о-^)

4A^zV Д Ф) f¹ - ^ехР (-^)] ’     (32)

где ЛФ) – амплитуда волны при распространении на расстояние z в отсутствие сцинтилляций, а ^аф – СКО флуктуаций фазы (17) МАт,Р^ = М; во фронте волны на выходе неоднородного ионосферного слоя (фазового экрана), определяемое СКО ^NN флуктуаций ПЭС ^N_T (р) ионосферы как [4]

О_ф=Ж%ЛС>^_т1с.Гй "          (33)

Выражения (31) и (32) связаны между собой зависимостью

4 (^z) = 4 (Ф + 4л 4) = Л² (^z) ^ехР (^-сгр )+ +Л² (Ф [! - ^ехР (-^ )] = Л² (4_;

которая наглядно показывает, что возрастание СКО флуктуаций фазы во фронте монохроматической волны на выходе неоднородного ионосферного слоя (33) ^Стф ~ ^аых приводит в результате дифракционных эффектов к уменьшению регулярной составляющей интенсивности поля данной волны в точке приема (31) 4 и пропорциональному увеличению интенсивности ее флуктуационной составляющей (32) ^фл ' Сумма же их, определяющая среднее значение интенсивности поля принимаемой волны (30) и (34) 4, остается величиной постоянной 4²Ф), не зависящей от ^сф ’ что соответствует закону сохранения энергии.

Очевидно, что интенсивность поля принимаемой волны в отсутствие сцинтилляций (когда согласно (33) при °кхт = О значение °Ф=^ определяется как ir^ = ^AVptKAA- (35)

Поэтому с учетом (35) выражение (34) для средней интенсивности поля принимаемой волны при трансионосферном распространении и наличии сцинтилляций можно записать в виде

2^=^X2[l-exp(-^)j = = <ехр(-2,7-1(Г3и)Я/./;г)

Л (^z) = ^ (^z) + ^фл (^z) = ^Pt^K_ac (^z)exp (X) + ^^p,K_nt (^z)[i - ехр(-<т^ )] = P_tK_oc (z).

x

-(8О,8тг<тДЛГг/с/о)" ,

Сравнительный анализ выражений (36) и (30) позволяет определить среднюю мощность ионосферных сцинтилляций:

< = kf =exp

[l-exp^")]-!.

Выражение (37) устанавливает аналитическую зависимость регулярной и флуктуационной составляющих мощности ионосферных сцинтилляций <=^(^.//0) от СКО мелкомасштабных флуктуаций ПЭС ионосферы через СКО флуктуаций фазы на выходе ионосферного фазового экрана (33) cr_p=8O,8^cr_A2Vr/cf_o .

Согласно (36) и (37) среднюю мощность сигнала на выходе приемной антенны (на входе приемника) при наличии ионосферного поглощения и сцинтилляций можно с учетом (26), (27) и (30) выразить через среднюю интенсивность поля принимаемой волны как

где K^ = G_tn_tG_rnX (^z) = GtntG,p_r^.

В более общем случае наклонного (tz_T<90°) РРВ через ионосферу в выражениях (40) и (41) необходимо дополнительно учесть увеличение пути РРВ в cosec a^ раз, что приведет к замене ^a№_T ■■ N_T иz соответственно на <7^! cosec a^, и N_Tcosec а_л и zcosec a_T .

Таким образом, искомая функциональная зависимость I «p ’ ²^« } ^ ^ (/0 , ^CTAN_T Л_Г , V₃ ) регулярной “p и флуктуационной 2 ст² составляющих коэффициента передачи трансионосферного КС по мощности от несущей частоты /0 передаваемого сигнала ССС и параметров ионосферы ^AN_T- N_T, Vj, определяющих проявление ее сцинтилляционных и поглощающих свойств, получена в виде совокупности выражений (40) и (41).

A^M^J/f^M^J.)/,,^//.-)/^

— ^oc (^)^цА-о — ^^oc (^) Ao ^exp(^—^ ) + (38) +^oc(^ZK[¹-^eXp(-^)]-

Это выражение с учетом равенства (14) U'KWX можно записать в более удобном виде

ргм-Р(КХ-ехр^у

+РЛХ

[1-ехр(-ст2)]

Сравнительный анализ (39) и (29) позволяет определить регулярную a^ и флуктуационную ^b составляющие коэффициента передачи трансионосферного многолучевого КС в следующем виде:

«p =^o^n^2exp(-^) =

= ^2ехр(-274(Г3йЛ/^)х

xexp

(80,8^<7ДЛГг/с/0)"

Выводы

Представлена комплексная модель распределения ЭК неоднородной ионосферы по высоте z и пространству Р = к^Х’>’У которую можно представить в виде (см. рисунок 3) совокупности трех слоев:

– однородного слоя с эквивалентной толщиной z₃, расположенного на высоте ^ ^m максимума ионизации и характеризующегося средним значением ПЭС (4) N_T==3N_m;

– расположенного на его нижней границе тонкого слоя, где происходят только столкновения электронов с ионами и нейтральными молекулами с эффективной частотой v₃;

– тонкого слоя неоднородностей, расположенного на высоте m максимума ионизации, который описывается статистическими характеристиками пространственных флуктуаций ПЭС NN_TX: нулевым математическим ожиданием (an_t (p)) =⁰ и постоянным СКО

/ 1—     \0,5       _

^Х^Ч P^N_m,– см. (6).

На основе анализа процесса РРВ (см. рисунок 4) от ИСЗ к ПРМ ССС через неоднородную ионосферу, описываемую разработанной комплексной моделью (см. рисунок 3) изменения ее ЭК по высоте и пространству, получены выражения (40) и (41), определяющие зависимости регулярной

^р и флуктуационной 2cr_g составляющих коэффициента передачи трансионосферного многолучевого КС по мощности от несущей частоты Уо передаваемого сигнала, среднего значения ПЭС ионосферы N_T и СКО его мелкомасштабных флуктуаций ^aAN_T '

Комплексная модель распределения ЭК неоднородной ионосферы и полученная зависимость И , 2<т; } = ^ (/₀, 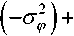№t , N_T,v₃) описывают структурно-физическую модель спутникового радиоканала с учетом поглощения и сцинтилляций волны в ионосфере. Работа выполнена при поддержке РФФИ в рамках выполнения проекта № 18 07 01020.