Структурно-функциональное моделирование тепловых режимов асинхронных двигателей в воздушной подушке при затоплении

Аварийное затопление судов и подземных шахт чревато большими человеческими жертвами, поэтому разработка электрических насосных установок, способных продолжать работу под водой до полного осушения затопленных объектов, решает актуальную проблему [11; 12; 19].

Целью исследования является разработка структурно-функциональной модели имитации затопленного асинхронного двигателя (далее – АД), работающего в воздушной подушке (см. Рисунок 1), для принятия управленческих решений, связанных с режимами эксплуатации осушительных установок.

Затопление АД связано с изменением физических факторов, которые по-разному влияют на тепловыделение, теплоотдачу и температуру электрических обмоток [3; 13; 21]. Применение системного подхода позволяет представить сложную организационно-техническую систему в виде взаимосвязанных функциональных подсистем (см. Рисунок 2), объединяющих в своем составе математическое описание различных физических явлений и процессов в АД [5; 8; 9; 15; 20].

Структурно-функциональная модель имитации работы АД под водой (см. Рисунок 2) соответствует варианту вентиляции, приведенному на Рисунке 1, г .

Конструктивная доработка для работы на значительных глубинах погружения обеспечивается созданием воздушной подушки за счет уплотнения корпуса АД, подачи сжатого воздуха внутрь плотной электрической полости и автоматического поддержания равенства давлений внутри и снаружи плотной полости [19; 21].

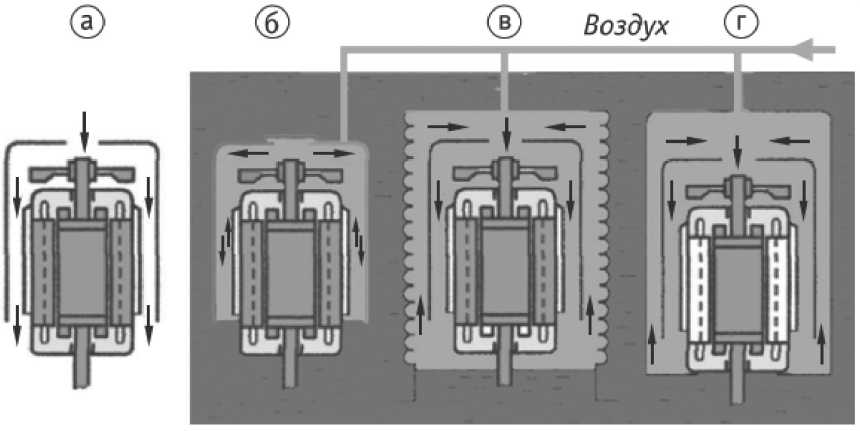
Рисунок 1. Вентиляция асинхронного двигателя: а – в нормальных условиях; б – в вентиляционном кожухе; в – в тубусе; г – в чехле модель асинхронного привода модель АД

ТЕПЛОВАЯ

Рисунок 2. Структурно-функциональная модель имитации асинхронного двигателя под водой

Входными данными модели являются: момент на валу АД, напряжение и частота питающей сети, исполнение системы вентиляции, глубина погружения при соответствующем давлении воздуха. Модель электропривода представлена моделями АД, рабочего механизма и энергетических показателей [16; 17]. Тепловая модель включает электротепловую модель, модели вентиляции и охлаждения, ресурса системы изоляции. Она построена на методе эквивалентных тепловых схем (далее – ЭТС), которая хорошо сочетается с вентиляционным расчетом, так как опирается на критерии Рейнольдса (Re), Нуссельта (Nu), Тейлора (Ta). Полная ЭТС закрытого обдуваемого двигателя позволяет определить превышение температуры различных частей АД [1; 2; 18].

Моделирование тепловых режимов АД

Узловые точки ЭТС: ВН – вентилятор; ВВш – внешний воздух перед вентилятором, за ним и над станиной; К – станина (корпус); Рот – клетка и зубцовый слой ротора; ВВТ – внутренний воздух; Щ – щит. Внешняя вентиляционная сеть двигателя представлена узлами ВВш, а внутренняя сеть – узлами ВВТ (см. Рисунок 3). Тепловыделение происходит в меди обмоток, расположенных в пазах статора (МП), в лобовых частях (МЛ), в стали

Структурно-функциональное моделирование тепловых режимов асинхронных двигателей ...

зубцов (З) и спинки (С) статора. В узлы МП, МЛ, З и С введены потери в пазовой и лобовой частях обмотки, в зубцах и спинке статора; узел ДП отвечает поверхности дна пазов. Узлы соединены соответствующими термическими сопротивлениями зубцов R ₃ , спинки R c , паза R „ , лобовых частей R „ , аксиальной обмотки R _a .

Рисунок 3. Полная ЭТС АД исполнения IP44

Теплота пазовых частей обмотки отводится к зубцам и дну паза через внутреннее сопротивление R _6m , n и сопротивление пазовой изоляции R „ , n . Другая часть теплоты лобовых частей отводится к воздуху через сопротивления R „ , каждое из которых является суммой внутреннего сопротивления обмотки R _{6m ё} , сопротивления изоляции R _{u ё} и конвективного сопротивления R _{a ё} . К зубцам теплота поступает также через воздушный зазор от ротора через сопротивление R _{a 3} , а от спинки в станину (корпус) - через контактное сопротивление R _K .

Источники тепла – это конструктивные элементы, где происходит потеря энергии. Электрические потери фазной обмотки определяются сопротивлением обмотки r и квадратом тока в ней I ² :

A P e = 1 2 r = 1 ² p l / F ,                                  (1)

где p - удельное электрическое сопротивление; l - длина проводника; F - поперечное сечение проводника.

Магнитные потери связаны с перемагничиванием активной стали от основного потока электрической машины:

A P m = k n ( P / M )_w /50 ⁶ 2 ( f /⁵⁰ ) 1,3 ^M ,                     (2)

где K n - поправочный коэффициент; ( P / M ) 10/₅₀ - удельные потери в стали на единицу массы при индукции 1 Тл и частоте 50 Гц; B – среднее значение индукции; f – частота; M – масса сердечника.

Вентиляционные потери определяются мощностью охлаждающего вентилятора как

A P v = Qp / П _г П _о б П мех ,                                        (3)

где Q - расход воздуха; p - полное давление вентилятора; п _г , П _О 6 , П _мех — гидравлический, объемный, механический КПД соответственно.

Эквивалентной тепловой схеме из n узлов отвечает совокупность алгебраических уравнений n

∑ ^ai , k ^Θ k ^{=∆ P}i ,                                     (4)

k = 1

где a_{i , k} – элементы матрицы, представленные термическими проводимостями ветвей ЭТС, Вт/К; Θ _k – температура узла k , К; ∆ P_i – потери в узле i , Вт.

Потери в узлах состоят из двух видов потерь ∆ P_i =∆ P_i ′+∆ P_{i 0} : потерь, не зависящих от температуры, – ∆ P _i ′ ; потерь, которые зависят от температуры, – ∆ P_{i 0} . Последние подсчитываются при температуре окружающей среды [7].

Диагональные элементы матрицы

n ai,i =∑-ai,k -βi∆Pi0                                         (5)

k = 1

k≠i учитывают зависимость потерь от температуры с помощью температурного коэффициента потерь βi , 1/К.

Элементы матрицы за пределами диагонали обратно пропорциональны термическому сопротивлению с обратным знаком:

a i , k | i ≠ k = - 1/ R i , k .                                                       (6)

Физическими основаниями для условий, определяемых соотношениями (4)–(6), является энергетический баланс в узлах и ветвях эквивалентной тепловой схемы.

Термическое сопротивление каждого элемента определяет его материал, геометрию и скорость потока воздуха [14].

Элементы машины, передающие тепло путем теплопроводности и не являющиеся источниками тепловыделений, представляются в тепловых схемах термическими сопротивлениями вида

R _λ = δ / λ S ,                                (7)

где δ – толщина плоской стенки элемента; λ – коэффициент теплопроводности материала при средней ожидаемой температуре; S – площадь, через которую проходит поток тепла.

Связи элементов машины с охладителем, где осуществляется передача тепла конвекцией, выражаются конвективными термическими сопротивлениями

R α = 1/ α S ,                                    (8)

где α – средний коэффициент теплоотдачи на поверхности площадью S.

Структурно-функциональное моделирование тепловых режимов асинхронных двигателей ...

Коэффициент теплоотдачи определяется числом Нуссельта и гидравлическим диаметром канала dã из уравнения a = Nu ■ X /d2,                                        (9)

где X = 0,0276 - коэффициент теплопроводности воздуха.

Критерий Нуссельта является неоднозначной функцией критерия Рейнольдса Nu = f ( Re ) , который представляет кинетическое подобие потоков или подобие полей скоростей в текущей вязкой среде:

Re = ® l ₀ / v ,                                       (10)

где to - условная скорость перемещения среды, в качестве которой принимается средняя скорость потока; v - кинематический коэффициент вязкости охлаждающей среды.

Критерии подобия Re и Nu вычисляются по характерным значениям параметров. При течении в каналах таким параметром 1 0 является гидравлический диаметр d ₂ = 4 F / П, где F – площадь сечения канала, Ï – его периметр.

Гидродинамика в воздушном зазоре 8 с учетом вращения ротора дополнительно оценивается числом Тейлора (Ta), Nu = f ( Re , Ta ) :

Ta = Re _mj 8 h 2 = ® r ₂ ⁰ ' ⁵ 8 1' ⁵ / v ,                           (11)

где r ₂ - радиус ротора; 8 - зазор между статором и ротором.

Температура в каждом узле, составляющем электрическую машину, находится с помощью системы алгебраических уравнений (9)–(11).

Результаты и обсуждение

Результаты расчета термических сопротивлений двигателя АО2-31-2 номинальной мощностью 3 кВт даны в Таблице 1, а превышения средних температур – в Таблице 2.

Таблица 1

Термические сопротивления элементов двигателя

№ п/п	Расчетные термические сопротивления полной ЭТС	Обозначение	Сопротивление, К/Вт
1	Воздуха над станиной (сторона привода)	R1	0,0083
2	Воздуха над станиной (сторона вентилятора)	R2	0,0079
3	Воздуха на входе в вентилятор	R5	0,0077
4	Наружный воздух – «свисающая» станина	R6=R8	0,227
5	Наружный воздух – станина над пакетом	R7	0,115
6	Наружный воздух – щит (сторона привода)	R11	0,719
7	Внутренний воздух – «свисающая» станина	R14=R22	4,509
8	Зубцы статора	R16	0,0096
9	Пазовая часть обмотки статора – зубцы	R17	0,181
10	Спинка сердечника статора – станина	R18	0,0245
11	Спинка сердечника статора – зубцовая зона	R19	0,023

Продолжение таблицы 1

12	Обмотка статора – дно пазов	R20	1,752
13	Наружный воздух – щит (сторона вентилятора)	R26	0,436
14	Лобовая – пазовая части обмоток статора	R29=R30	0,0472
15	Внутренний воздух – лобовая часть обмотки	R31=R33	0,937
16	Ротор – воздушный зазор – сердечник статора	R32	0,1554
17	Внутренний воздух – подшипниковый щит	R35=R38	0,267
18	Внутренний воздух – ротор	R36=R37	0,772

Таблица 2

Превышение средней температуры элементов двигателяАО2-31-2

№ п/п	Элементы тепловой схемы двигателя	Обозначения	Превышение температуры, Δθ °С
1	Лобовая часть обмотки статора	Δθ м, л	75,93
2	Пазовая часть обмотки статора	Δθ м, п	74,53
3	Ротор асинхронного двигателя	Δθ рот	207,9
4	Сердечник статора двигателя	Δθ с, ст	36,37
5	Внутренний воздух двигателя	Δθ в, вт	62,56
6	Корпус асинхронного двигателя	Δθ к	44,98
7	В среднем по обмотке статора	Δθ м	80,87

Натурным испытаниям в воздушной подушке под давлением подвергались электрические двигатели, технические характеристики которых приведены в Таблице 3.

Таблица 3

Технические характеристики исследуемых двигателей

Тип двигателя	Напряжение, В	Сила тока, А	Частота тока, Гц	Полезная мощность, кВт	Частота вращения, об/мин	сosφ	КПД, %	Предельно допустимая температура, °C
АО2-31-2	220/380	11/6,1	50	3,0	2880	0,89	84,5	120
АОМШ-21-2	380	1,75	50	0,7	2790	0,88	66	180
АОМШ-22-4	380	2,14	50	0,7	1370	0,8	66	180

АД нагружался в воздушной камере с постоянной температурой и установленным давлением. Нагрузка в длительном режиме регулировалась с помощью электромагнитного тормоза, установленного на валу двигателей [4; 6; 10].

Измерялось давление воздуха (Ра), потребляемая из сети мощность Р (кВт), электрический ток I (А), скорость вращения n (об/мин), превышение температуры изоляции лобовой части обмоток Δθ (°С) над температурой окружающей среды θ (°С). Давление воздуха поднималось до значения 11×10⁵ Ра, что соответствует рабочей глубине погружения более 100 м. По результатам исследований, представленных на Рисунке 4, можно произве-

Структурно-функциональное моделирование тепловых режимов асинхронных двигателей ...

сти анализ зависимостей изменений тепловых режимов двигателей от давления внешней среды и нагрузки.

С ростом давления Ра улучшается конвективный теплообмен и охлаждение, поэтому температура перегрева Δθ (°С) снижается. При синхронной частоте вращения до 1500 об/мин это способствует использованию АД AOMШ-22-4 с перегрузкой в 1,5…2 раза.

Рисунок 4. Результаты исследования АД

Одновременно растет кинематическая вязкость воздуха, потери на вентиляцию и дополнительный нагрев, что характерно для АД с синхронной частотой вращения 3000 об/мин (AO2-31-2, AOMШ-21-2). При повышении давления до 1,1 мПа (глубина более 100 м) потребляемая мощность АД A02-31-2 возрастает на 30 %, а АД AOMШ-21-2 – на 40 %. При давлениях 0,3…0,5 мПа температура перегрева Δθ (°С) этих АД замедляет снижение, а при 0,6…0,8 мПа начинает возрастать. Поэтому при частотах вращения более 1500 об/мин на глубине свыше 50…60 м рекомендуется снижение нагрузки для соблюдения температурного режима и сохранения ресурса изоляции.

Выводы

Промышленные электрические машины способны надежно работать на значительных глубинах при соответствующей доработке их конструкции. Теоретическая имитационная модель позволяет достоверно определять и прогнозировать температурные режимы асинхронных двигателей, работающих в воздушной подушке на различных глубинах затопления. Полученные результаты являются основанием для принятия решений о нагрузочных режимах эксплуатации затопленных насосных установок для осушения объектов и сохранения ресурса электрической изоляции приводных двигателей.