Структурно-топологические особенности диаграмм ритма сердца

Исследование физического процесса начинается с того, что экспериментатор с неизбежностью переводит непрерывный физический процесс в его дискретный аналог в форме цифрового ряда, который характеризуется двумя интервалами времени: минимально возможный определен шагом дискретизации, максимально возможный равен размеру ряда. При регистрации электрокардиограммы (ЭКГ) с частотой сканирования 500 Гц шаг дискретизации ∆x = 1 мс. На диаграмме ритма сердца (ДРС) все значения RR-интервалов распределены по фиксированным ярусам [1].Формы структури- зации ДРС по двум ортогональным направлениям разные. По вертикали – структуризация ярусная, а по горизонтали на каждом ярусе – цуговая [1-2]. Ярус-цуговая структура указывает на структурнотопологическое формирование ДРС [2].

Известно [3], что биоритмы составляют целостную функционально-связанную систему ритмических элементов и подсистем, а в ритме сердца закодирована информация обо всех процессах в организме [4]. В этой системе единицей времени становится интервал времени одного кардиоцикла, как один событийный отсчет.

Объектом исследования является цифровой ряд последовательности значений RR-интервалов на ЭКГ. ДРС по оси значений имеет ярусную структуру, а ось времени представлена последовательностью номеров отсчетов.

Целью работы является исследование ярусной структуры ДРС и ее дифференциальных рядов (ДР) для определения общих закономерностей ее формирования.

Дифференциальные ДРС

Регистрации ЭКГ проводились лицензированным комплексом амбулаторной регистрации электрокардиосигнала «AnnAFlash 3000» [5] во втором грудном отведении для группы здоровых молодых людей обоих полов с преобразованием в программе «EScreen» [6] в цифровые ряды последовательности значений RR-интервалов. Далее в работе представлены результаты обработки и анализа цифрового ряда RR-интервалов, ДРС и ДР одной обследуемой Е-вой. Результаты по другим обследуемым полностью совпадают с приведенными.

На рис. 1 а представлена ДРС и ее горизонтальная гистограмма. Видно, что фазовые ярусы ДРС не равноценны, распределение не равномерное, близкое к распределению Гаусса с левосторонним смещением.

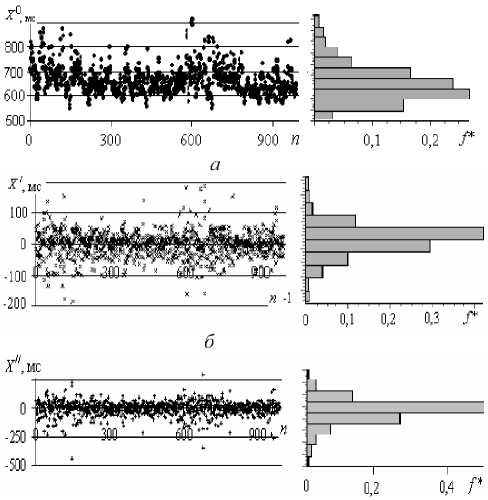
Рис. 1. Графики ДРС Е-вой (•) и ее гистограммы ( а ), дифференциальной ДРС ( х ) и ее гистограммы ( б ) и второй производной (+) и ее гистограммы ( в )

Алгоритмическую информацию о микропереходах на ярусной ДРС должна содержать дифференциальная ДРС (дДРС) [7]. Ее графическая диаграмма также имеет ярусную структуру с тем же шагом дискретизации (см. рис.1б). Цифровой ряд дДРС функции пошаговой скорости (Δ X /Δ n )формировал-ся по цифровому ряду исходной ДРС в форме последовательности отношений разности следующего и данного значения RR-интервала (Δ X = RR _i+1 – RR _i) к разности их номеров Δ n = 1. Каждый член цифрового ряда дДРС представляет также величину тангенса угла α_j наклона линии интерполяционной связи: tg a j = A X i / A n . ДДРС,полученная конечноразностным методом представляет цифровой ряд величин пошаговых скоростей изменений RR -интервалов, или микропереходов между соседними отсчетами (рис.1 б ).

Если продлить эту логику и составить цифровые ряды дДРС с возрастающей степенью i производной (рис. 1 в ), то возможно получить информацию о скрытой внутренней динамике формирования ДРС.

При формировании ярусной ДРС координатная точка совершает сложные дискретные движения по вертикальной оси значений RR- интервалов около среднего значения. Вертикальное движение разворачивается по горизонтальной оси номеров отсчета. Результатом разложения функциональной зависимости X ( n ) вертикального движения координатной точки на плоскости ДРС в ряд Тейлора около среднего значения является степенной знакочередующийся ряд: X ( n ) = X 0 - X 1 n + X 2 n ² -... ± X k n k . Здесь n -текущее значение по номерной шкале отсчетов, X ₀ – выборочное среднее значение RR -интервала ( X _ср), X _i. n ⁱ – величины аддитивного отклика ритма на влияния со стороны независимых регуляторных механизмов. При каждом акте дифференцирования степени i теряют единицу, а ряд теряет один член. Именно так и происходит при первом дифференцировании исходного ряда ДРС с шагом отсчета 1 (см. рис. 1 б ). Однако, начиная уже со второго акта дифференцирования, возникают трудности не только в трактовке получаемых результатов, но даже в определении получаемых объектов. ДРС и дДРС представляют разные объекты: ДРС – последовательность значений RR-интервалов на ЭКГ, а дДРС – последовательность величин микропереходов на ДРС.

Для сохранения смысла термина необходимо при формировании дДРС пользоваться не последовательной процедурой разностей соседних значений микропереходов, а процедурой их суммирования. Только в таком случае можно получить цифровой ряд величин микропереходов при шаге отсчета, равном 2. Последующая подобная процедура приведет к формированию цифрового ряда величин микропереходов при шаге отсчета, равном 4 и т.д. При этом получаются цифровые ряды которые адекватны термину дДРС, но с разным шагом отсчета и, соответственно, уменьшающимся размером.

Такая технология формирования дДРС с растущим шагом дискретизации позволяет исследовать определенные шагом отсчета межъярусные связи. Иными словами, указанная последовательность элементарных процедур суммирования является простейшим технологическим фильтром высоких частот. Очевидно, что в результате применения этой технологии после k-той процедуры суммирования на графике дДРС выделятся долгопериодические составляющие процессы ритма [8].

Если же последовательно применять процедуру дифференцирования ярусного объекта конечно-разностным методом, то последующие объекты, начиная со второго акта, не могут быть обозначены как дДРС, так как приобретают совершенно иной смысл. Первый из них ( i = 2) представляет цифровой ряд последовательных разностей между соседними величинами микропереходов на ДРС. Далее ( i > 2) члены, получающихся цифровых рядов ДР, представлены последовательными разностями соседних пар членов предыдущего цифрового ряда, со значением i , меньшим на 1. Именно такая технология обработки цифровых рядов представляется наиболее перспективной.

По 18 последовательно примененных процедур дифференцирования исходной ДРС получено 18 цифровых рядов X ^{( i}) ( n ) . Объем каждого последующего ряда меньше на единицу предыдущего. С ростом степени i производной на графиках функций X ⁽ i ) ( n ) отчетливо проявляются периодические топологические структуры разной продолжительности. Начиная с i = 8-9, качественный характер ДР не меняется, а топология структур становится более контрастной (см. рис. 2). На диаграммах ДР отчетливо видны области узлов и пучностей.

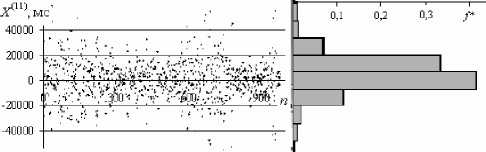
а

б

Рис. 2. Диаграммы ДР и их гистограммы при i = 11

( а ) и i = 16 ( б ) по исходной ДРС (см. рис. 2 а )

Для сопоставления получаемых результатов использовалась виртуальная ДРС (вДРС, или V ), полученная генерацией случайных чисел по нормальному закону с параметрами объема выборки, дисперсии и среднего значения реальной ДРС (или R ) [2; 8] и представляющая ритм «неуправ-

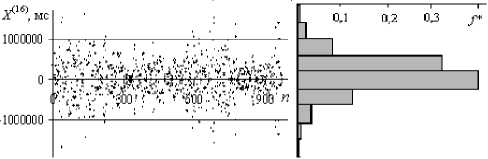
По всем 19 рядам с учетом исходной ДРС в программе «Entropy & Calculation» [8] рассчитаны количество информации I _Σ и получены 19 цифровых рядов функции оконной энтропии I _o( n ) [8]. Каждый цифровой ряд исходной ДРС, дДРС и ДР характеризуется четырьмя параметрами: средним значением X _ср, стандартным отклонением σ_X, пошаговым отношением σi+1/σi и информационной энтропией I * = I _Σ/ n . Каждый цифровой ряд оконной функции I _o( n ) дает еще два параметра: средне-оконное значение количества информации I _oср и стандартное отклонение σ _{I 0} для ряда I_o( n ). Во всех случаях n – размер параметрического ряда.

а

б

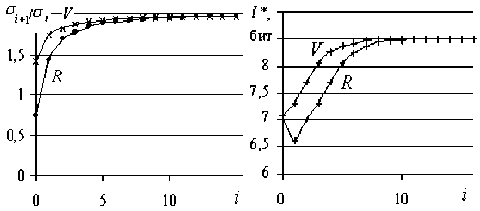
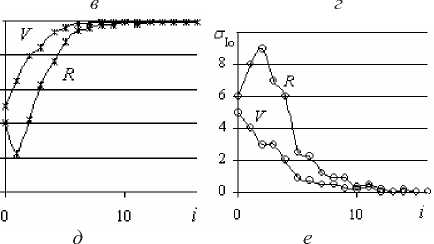
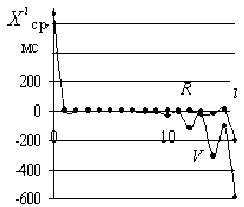
Рис. 3. Функциональные параметры ДР вДРС ( V ) и ДРС ( R ) УЗО Е-вой (см. рис. 2). I *_max = 8,5, I _{о ср} = 524,76 при n ₀ = 100

При степени i = 0^1 функция Xс(р) (i) сильно меняет качество (см. рис. 3а). При этом изменение функций с(i) и I*(i) I(i) и сI0 (i) для R и V (см. рис. 4б-г) противоположное. На графиках рис. 4б-е видно, что кривая R имеет характерные отличия при i = 0…2 по сравнению с ходом кривой V. При i > 2 все функции ведут себя качес- ляемого сердца».

твенно одинаково, так, что при сдвиге влево на

шаг i = 2 кривой R графики кривых ( R и V ) практически совпадают.

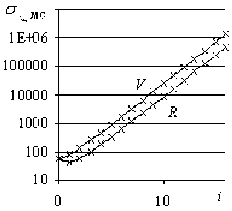
С ростом степени i функция σ( i ) растет круто экспоненциально для всех i > 1 (см. рис. 3 б ), а отношение σ_i+1/σ_i растет с насыщением, приближаясь функционально к геометрической прогрессии с множителем 2 (см. рис. 3 в ).

Качественное изменение функции X^ (i) вновь проявляется при i = 8…10 и характеризуется экспоненциальным ростом и заметное расхождение обеих функций. При этом функции I *( i ), I _oср ( i ) и σ_i+1/σ_i( i ) стремятся к насыщению, а стандартное отклонение оконной функции количества информации σ_I0( i ) падает до нуля и далее не меняется. Это является признаком стационарного процесса и означает, что сама техника обработки не влияет на изменение величин I _Σ и I * – показателей хаотической составляющей ритма.

Постоянный экспоненциальный рост функции о( i ) и расхождение функций X^ (i) для обоих случаев ( V и R ) трудно понять в терминах микропереходов дДРС, поэтому представим технологию последовательного дифференцирования ДР, используя исходный термин RR-интервала ДРС. Итак, с ростом степени i последовательно формируются цифровые знакочередующиеся ряды. Каждый член i -го дифференциального ряда (ДР) организован суммой i членов с постоянными коэффициентами. Представляя эти коэффициенты членами матрицы, обнаруживаем, что каждый коэффициент новой строки является разностью коэффициентов данного и предыдущего столбца предыдущей строки. Например, –462 = –252 –210 (см. таблицу).

Таблица. Коэффициенты первого члена ДР

i	X 0	X 1	X 2	X 3	X 4	X 5	X 6	X 7	X 8	X 9	X 10	X 11
0	1
1	1	–1
2	1	–2	1
3	1	–3	3	–1
4	1	–4	6	–4	1
5	1	–5	10	–10	5	–1
6	1	–6	15	–20	15	–6	1
7	1	–7	21	–35	35	–21	7	–1
8	1	–8	28	–56	70	–56	28	–8	1
9	1	–9	36	–84	126	–126	84	–36	9	–1
10	1	–10	45	–120	210	–252	210	–120	45	–10	1
11	1	–11	55	–165	330	–462	462	–330	165	–55	11	–1

По содержанию и технике заполнения мат-

( a - b ) i , где к - номер значения RR -интервала ( X ). Таким образом, каждый член ДР является биноминальным рядом с i членами и с коэффициентами, определяемыми в соответствующей строке треугольника Паскаля.

При определении среднего значения ДР, суммированные биноминальные ряды дадут алгебраическую сумму строки для каждого члена суммирования при k ≥ i , которая для данного случая всегда равна нулю. Поэтому величина X _ср определяется алгебраической суммой членов с k <  i . При этом, чем меньше k , тем меньше данный член испытывает компенсационное действие со стороны соседей. Рост величин коэффициентов с ростом i , а также чередование их отрицательных и положительных значений, приводит всегда в конечном итоге к росту общего числа ярусов при постоянстве числа «рабочих» ярусов на ДРС и постоянному расхождению функции X(i) и росту σ( i ) по форме аналогичной нелинейному самовозбуждению колебательной системы.

Последовательное дифференцирование ДРС означает поиск связей между каждым первым значением RR -интервала в выборке и k -тым, но уже с учетом зависимости от промежуточных значений. С ростом i зависимость от промежуточных значений растет за счет роста величин коэффициентов влияния.

рица является арифметическим треугольни-

ком Паскаля для биноминальных коэффициен-

тов

^C i ^k

k !( i - к )!

разложения двучлена вида

При росте i коэффициент асимметрии А, не равный нулю для распределения исходной ДРС, падает до нуля для знакопеременных рядов ДР в

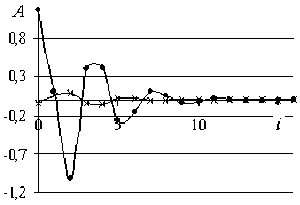
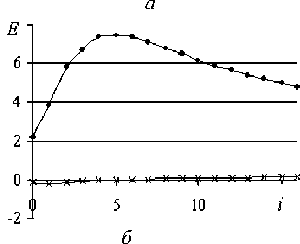
Рис. 4. Графики функций асимметрии A ( i ) ( а ) и эксцесса E ( i ) ( б ) для реальной (•) и виртуальной ( х ) ДРС (см. рис. 2)

виде затухающего колебания в интервале i = 0…8. При этом эксцесс Е растет и имеет максимум при i = 4 (см. рис. 4 а-б ).

Это означает, что микропереходы на ярусах ДР происходят преимущественно между соседними ярусами и сконцентрированы около нулевого значения. Стремление к симметрии распределения значений ДР характерно для распределения Гаусса (см. рис. 4 а ), но в отличие от виртуальной ДР, кривая распределения плотности вероятностей реальной ДР быстро вытягивается до максимального значения при i = 4 и далее медленно спадает (см. рис. 4 б ).

Анализ ДР в программе САДР2 [2; 8] показал, что с ростом i максимум узкополосного спектра плотности мощности ДР быстро смещается в сторону высоких частот (от 2.10^-3 Гц к 0, 47 Гц). Вклад низких частот становится пренебрежимо малым. График автокорреляционной функции ДР приобретает форму АКФ хаотического процесса, а топология фазового портрета видоизменяется от формы «клубка» до формы узкого «веретена». Это указывает на возможность смены базовой динамики ритма от шума Гаусса – к броуновскому движению [9].

Обсуждение результатов

Каждый член рядов ДР степени i содержит информацию об определенном величиной i количестве соседних членов исходного ряда ДРС. При i = 8-9 количество соседних членов исходного ряда ДРС, представляющих один член ряда ДР степени i , также равно 8-9.

Для ДР степени i = 8-9 и выше значения I* и I0ср перестают расти. Поведение I*(i) определяется насыщением к величине I*max. Функция сI0 (i) определяет интенсивность реакционной изменчивости (перенастройки) ритма на управляющие воздействия. По значению сI0 (i) = 0 при i > 9 определяется отсутствие влияния на структурную неупорядоченность ритма внешних регуляторных механизмов и ее сохранение.

Это может означать, что ДР не меняет своего качества при дальнейшем росте i . Величина критерия I * пошагового перебора вариантов при формировании ДР стремится к величине I *_max при i = m , вероятно, являющейся информационной коммуникационной единицей структуры и оценкой энтропийной размерности связи между членами исходного ряда ДРС. Это, в свою очередь, означает, что cкрытое во внутренней динамике и недостающее для описания динамической системы количество информации, становится открытым и учитывается полностью.

Чем выше минимальная величина степени ( i = m ), тем более сильны дальние связи. Без внешнего управления критерий неупорядоченности ДР ( I _Σ) перестает меняться с ростом i и линейно зависит от объема выборки ДР.

У здоровых людей в норме непрерывно задействуется большое число дальних связей между отсчетами «по горизонтали» ДРС. Чем большее число независимых регуляторных механизмов «включено», тем больше дисперсия исходной ДРС, поэтому при росте дисперсии RR-интервалов дальность связей на ДРС падает, и, наоборот.

В рассмотренном примере (рис. 1 – 3) по качественному изменению параметров ДР выделяются следующие значения i : 1; 2; 4 и 8-9. Дыхательный центр может отвечать в качестве регулятора за связь RR -интервалов 0 – 4 – 8 (в норме). При учащенном дыхании интенсивность влияния этого регуляторного механизма и дальность связи RR -интервалов падает. Это может объяснить волнообразный характер графика функции с I 0 ( i ) и ее затухание при росте i . Чем меньше величина i , при котором с I 0 ( i ) = 0, тем меньше подверженность ритма перенастройке извне. Это косвенно подтверждает заключение авторов [4; 8;, 10] о существовании иерархии систем регуляции и управления ритмом сердца.

Исходя из вышесказанного, можно провести следующую аналогию: рост величины i аналогично открытию «замков» системы регуляции и управления ритма сердца.

Выводы

Автор полагает, что при росте i каждая последующая ДР «включает» прямую информацию о последующем уровне регуляции (управления) в их иерархии, но исключает информацию о предыдущем уровне. Если это так, то размерность m определяет число действующих независимых контрольно-регуляторных механизмов. В рамках такого представления размерность m оценивается числом i = 8-9, при которой «исключается» принципиальная возможность работы механизмов внешней регуляции ритма сердца, так как базовая динамика ритма меняет свое качество от шума Гаусса – к броуновскому движению.

В этом смысле шум Гаусса определяет «форму» хаотической составляющей ритма сердца и является динамической базой процессов контроля, регуляции и управления. Броуновское движение определяет «очищенную форму» хаотической составляющей ритма сердца.

Для процесса броуновского движения характерно полное отсутствие ближних и дальних связей между отсчетами. Для процесса, характеризуемого шумом Гаусса, превалируют неограниченные дальние связи между отсчетами. Для процесса детерминированного хаоса (ритм сердца) превалируют ограниченныепеременные связи между отсчетами, определенные влиянием того или иного механизма контроля, регуляции и управления. Количество соседей, «цепляемых» данным кардиоциклом может служить мерой m детерминизма ритма сердца. При росте i происходит последовательная потеря детерминизма. При росте m устойчивость ритма растет, «горизонт предсказуемости» ритма падает, а уровень функционального состояния организма растет. Уменьшение m приводит к росту риска внезапной сердечной смерти.

Превалирование в ритме сердца хаотической составляющей в форме шума Гаусса при росте m может означать проявление дальних связей между отсчетами на ДРС (механизмы контроля) и слабое участие ближних связей (механизмы регуляции и управления) в формировании ритма сердца.