Структурно-устойчивые трёхмерные и двумерные лазерные половинные пучки Пирси

Явление дифракции – это одно из проявлений волновой природы света. Когда световой пучок распространяется вдоль оптической оси от начальной плоскости к плоскости наблюдения (обе плоскости параллельны друг другу и перпендикулярны оптической оси), световые поля, исходящие от разных участков начальной плоскости, интерферируют друг с другом и в плоскости наблюдения возникает дифракционная картина, распределение интенсивности в которой в общем случае отличается от распределения в начальной плоскости. Распространение светового пучка в однородной среде описывается уравнением Гельмгольца и его параксиальным приближением – уравнением типа Шрёдингера. Несмотря на дифракцию, у этих уравнений существуют решения, описывающие световые поля, которые свободны от этого явления. В первую очередь, это давно известные традиционные и недавно открытые асимметричные пучки Бесселя [1 –3], Матье [4] и Эйри [5]. Пучки Бесселя распространяются без дифракции в трёхмерном пространстве, а пучки Эйри – в двумерном. Также не обладают дифракцией плоские волны, так как распределение интенсивности у них не меняется при распространении от одной плоскости к другой. В трёхмерном случае не обладает дифракцией любое световое поле, угловой спектр плоских волн которого отличен от нуля на бесконечно тонком кольце [1]. Наряду с пучками Бесселя и Эйри, интерес представляют параксиальные структурно-устойчивые пучки, инвариантные к распространению. Такие пучки не являются бездифракционными, но при распространении структура их распределения интенсивности в поперечной плоскости не меняется, меняется только масштаб. Наиболее известными пучками такого типа являются пучки Эрмита–Гаусса и Лагерра–Гаусса [6], гипергеометрические моды [7]. В работе [8] рассмотрены пучки Пирси как трёхмерные аналоги пучков Эйри. Распределение комплексных амплитуд таких пучков описывается функцией Пирси [9, 10], опреде-

ляемой как интеграл от комплексной экспоненты, аргумент которой является полиномом (подобно функции Эйри). Угловой спектр таких пучков представляет собой параболу с фазовой модуляцией. Эти пучки обладают свойством автофокусировки и восстанавливаются после искажения препятствиями. В недавно опубликованной работе [11] предложен виртуальный источник, формирующий пучок Пирси.

В данной работе проводится обобщение функции Пирси и рассматриваются структурно-устойчивые половинные пучки Пирси (ПП-пучки). Обычные пучки Пирси [8] являются суммой двух ПП-пучков первого порядка. Угловой спектр ПП-пучков представляет собой не параболу (как у пучков Пирси из [8]), а только одну её половину. Также рассматриваются двумерные аналоги пучков Пирси, обладающие ускоряющейся (искривлённой) траекторией.

1. Трёхмерные половинные пучки Пирси

Комплексная амплитуда параксиальных световых пучков Пирси [8] в начальной плоскости имеет вид:

E ( x, У, z

= 0 ) = Pe 1^,

I x 0 У 0.

+~

= j exp is ⁴

—M

+ is ²

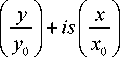
d s .

В [8] показано, что при распространении структура пучка не меняется, происходит лишь сдвиг центра пучка вдоль одной декартовой координаты и масштабирование по обеим декартовым координатам, причём масштаб по осям x и y разный:

E (x, y, z ) =

< xPe

(1—z^x x У — У0 z/ (2 kx02)

( x 0 ( 1 — zlz e )^^ У 0 ( 1 — zlz e )^" J

,

где z e = 2 ky 0 ².

При z = z _e комплексная амплитуда имеет вид:

E ( x , У , z e ) =

i n

2 exp

У/У 0 ^- ( У 0/ x 0 )

- iy 0 x²

4 ( x 2 У о — У 0 )

В конце работы [8] приводится обобщение пучков (1) в виде пучков с комплексной амплитудой в начальной плоскости, описываемой функцией

+^

U ( x,y ) = J exp[i( s² + ys^K + xs™ )]d s ,

-^

причём при n = 2 m такие пучки являются структурноустойчивыми. Числа n и m должны быть целыми. Требование целочисленности следует из того, что интеграл в (3) берётся по всей числовой оси, поэтому при дробных значениях n и m при s <0 экспонента может стать вещественной и устремиться к бесконеч-

ности при s → –∞.

Вывод выражения (2) из (1) осуществляется с помощью преобразования Френеля, при вычислении которого используется замена переменной интегрирования, причём пределы интегрирования не меняются, так как они бесконечны. Однако, если бы нижний предел был равен нулю, при замене переменных пределы также не поменялись бы, поэтому наряду с (1) и (3) можно рассмотреть половинный пучок Пирси v -го порядка, который также не меняет свою структуру при распространении и который в начальной плоскости имеет комплексную амплитуду:

E (x, y, z = 0) = HPe v I —, ^ I =

I x 0 У 0 J

= J exp [ is⁴ v + is² v ( y/y ₀ ) + is v ( x/x ₀ ) ] d s .

В произвольной плоскости комплексная амплиту-

да такого пучка примет вид:

E (x, y, z ) =

< x HPev

x(1 -Vz, Г'1

x У ^- У 0 ^z / (² kx 02 ) '

l x 0 ( 1 — Z/ Z e

J12

= J

.

Заметим, что в отличие от (3) в (4) уже не требуется целочисленности параметра v , так как интеграл берётся только по положительным значениям переменной интегрирования s .

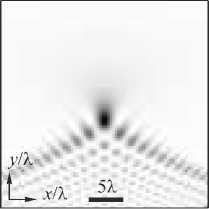
Дифракционная картина пучков (5) в поперечной плоскости имеет вид наклонных световых линий, дифракционной толщины (рис. 1 а ). Функция HPe _v ( x / x ₀, y / y ₀) была рассчитана тем же способом, что и в работе [8], т.е. использовался поворот контура интегрирования в комплексной плоскости, только вместо замены переменных s ^ s 'exp(i n /8) была замена s ^ s 'exp(i n /(8 v )). При вычислении были использованы следующие параметры: длина волны % = 532 нм, x 0 = у 0 = % , v = 1.

Угловой спектр ПП-пучка v -го порядка имеет вид:

E ( k x ,k y ) =

xr(-k-x0)l; exp (ik;x0 )x x8(k2x2 + kyy0 ), kxx0 < 0, 0, kxx0 > 0.

Как и в работе [8], угловой спектр (6) отличен от нуля на параболе k x x 0 + k_yy ₀, однако не на всей параболе, а только на её половине (при k_xx ₀< 0).

Пучок Пирси с начальным полем (1) является линейной комбинацией ПП-пучков (4) первого порядка:

| ^х   V I            ( ^х   V I           (    ^х   V I

Pel —, I = HPe 1I — , — I + HPe 1 I-- ,^- I . (7) l ^x 0   у 0 J         l ^x 0   y 0 J        l   ^x 0   y 0 J

Это также видно и из рис. 1 а , б : пучок Пирси из [8] является результатом интерференции ПП-пучка из рис. 1 а и его зеркального отражения относительно плоскости x =0. Заметим, что слагаемые в (7) описывают два

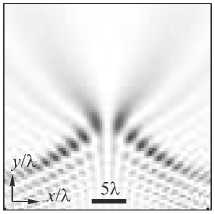
пучка, при распространении которых их амплитуды приобретают лишь множитель, зависящий от y ₀², т.е. одинаковый для обоих пучков . Поэтому коэффициенты в линейной комбинации могут быть произвольными, и, тем не менее, пучок будет сохранять свою структуру. В частности, можно рассмотреть в (7) вместо суммы разность, и тогда получится пучок, аналогичный пучку Пирси в [8], но в центре вместо максимума интенсивности будет минимум. Интенсивность разницы двух симметричных относительно плоскости x =0 ПП-пучков показана на рис. 1 в .

б)

в)

Рис. 1. Распределение интенсивности (негатив) ПП-пучка при v = 1 (а), полного пучка Пирси из [8] (б) и разности симметричных ПП-пучков с нулевой интенсивностью в плоскости x = 0 (в)

На рис. 2 показаны те же дифракционные картины, что и на рис. 1, но для случая дробного порядка v = 1,5.

Из рис. 2 видно, что с ростом порядка функции Пирси v дифракционная картина принципиально не изменилась, хотя при v = 1,5 к краю картины локальные максимумы интенсивности спадают быстрее.

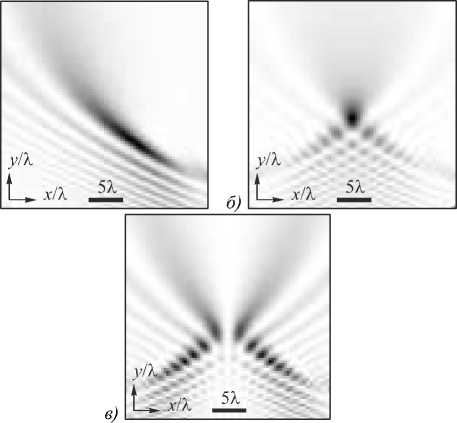
Рис. 2. Распределение интенсивности (негатив) ПП-пучка при v = 1,5 (а), полного пучка Пирси из [8] (б) и разности половинных ПП-пучков с нулевой интенсивностью в плоскости x = 0 (в)

Заметим, что при получении (5) из (4) замену переменной интегрирования можно делать только для z <  z e , в противном случае пределы становятся мнимыми. Однако можно показать, что

( V 3            ..I ( V3..I

EI x, ~ + n, ze + Z I = E I -x, ~ - n, ze — Z I,(8)

V x о            7 V    x о т.е. подобно пучку Пирси [8] после прохождения пучка через плоскость z = ze распределение интенсивности является зеркальным отражением распределения интенсивности до плоскости z = ze относительно плоскостей x =0 и y = y03/x02.

В заключение данного раздела заметим, что комплексные амплитуды двух трёхмерных ПП-пучков с параметрами ( x 01 , y 01 ) и ( x 02 , y 02 ) ортогональны при условии, что у_о21у 01 ^ x 22 / x 21 . Это условие может быть получено как непосредственно с помощью скалярного произведения функций HPe _v ( x / x ₀₁, y / y ₀₁) и HPe v ( x / x 02 , y / y 02 ), так и из того, что при данном условии угловые спектры плоских волн (6) отличны от нуля на разных непересекающихся параболах.

2. Двумерные половинные пучки Пирси

Аналогично (4) можно рассмотреть 2D ПП-пучки, комплексная амплитуда которых в начальной плоскости имеет вид:

+^

E ( x ,0 ) = J exp

= HPe p°

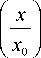
isp

+ is ² p

С помощью преобразования Френеля можно показать, что на некотором расстоянии z комплексная ам- плитуда станет равна

+^

E ( x , z ) = J exp

I x I -I — I is p I I + 1 I 1-- 2 I s ^{2 p}

V x о 7 v    2 kx о 7

d s . (10)

Сделаем замену переменной интегрирования s = (1 – z / z_e )^{–1/(2 p )} t , где z_e = 2 kx ₀². Тогда вместо (10) получим для комплексной амплитуды 2D ПП-пучка:

E ( x , z )

( 1 — Z/Z e /⁽² p ^P

X

x HPe p°

x

V x 0 ( 1 - ' ) 7

Как и в трёхмерном случае, здесь замену переменной интегрирования можно делать только для z <  z_e . В противном случае пределы становятся мнимыми. Но из (10) следует, что

E ( x , Z e +Z ) = E * ( - x , Z e -Z ) ,                     (12)

где Z — расстояние вдоль оси z от фокальной плоскости, т.е. после прохождения 2D ПП-пучка через плоскость z = z e распределение его интенсивности является зеркальным отражением распределения интенсивности до плоскости z = z e относительно оптической оси.

Из (11) видно, что в начале распространения (до фокальной плоскости z = z_e ) в любой поперечной плоскости z <  z_e координаты максимумов интенсивности 2D ПП-пучка определяются по формуле:

x max = Vmx о 1 - — , (13) ze где ym – координата m-го максимума функции |HPep° (x)|2. Дважды продифференцировав (13) по z, получим, что при z < ze будет выполняться неравенство (dxmax/dz)(d2xmax/dz2) >0, что свидетельствует о наличии ускорения траектории пучка перед фокусировкой. Из свойства симметрии (12) следует, что после прохождения через плоскость z = ze 2D ПП-пучок начнёт распространяться с замедлением.

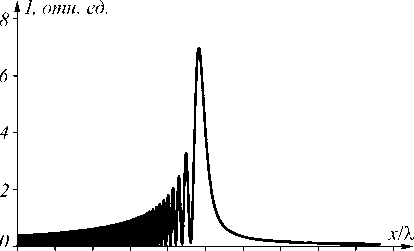
Рассмотрим распространение 2D ПП-пучка при p = 2. Пусть % = 532 нм, x _о = % . Тогда z _е = 4 л% . На расстоянии z = 3 z _e/4 пучок сужается в два раза, в нашем случае это расстояние равно z =3 п% . Максимальная интенсивность при этом увеличивается в два раза. В плоскости z _e = 4 n% поле (11) «бесконечно» сужается, и возникает фокус. Для выбранных параметров интенсивность в начальной плоскости имеет вид, показанный на рис. 3 а . Моделирование проводилось конечно-разностным методом распространения пучка (BPM-методом) в области -8о % <  x < 8о % , о <  z < 3о % . На рис. 3 б показано рассчитанное распределение интенсивности в плоскости Oxz . На рис. 3 в, г показаны сечения интенсивности (рис. 3 б ) при z =о (рис. 3 в ) и z = 75 % /8 (=3 л% ) (рис. 3 г ). Из рис. 3 видно, что пучок действительно сузился в два раза: при z =0 координата четвёртого нуля равна примерно -1о % , а при z = 75 % /8 она равна примерно -5 % . Максимальная интенсивность на рис. 3 г в два раза выше максимальной интенсивности на рис. 3 в .

Кроме того, видно, что и на рис. 3 в , и на рис. 3 г интенсивность второго максимума примерно в два раза меньше интенсивности главного максимума, что также демонстрирует изменение светового пучка при распространении только в масштабе, но не в структуре.

z/X

30- а) SO -40 -30 -20 -10 0 10 20 30 40 50

25-

20-

15- z.

10-

x/X

б)   -20 -15 -10 -5 0   5 10 15 20

I, отн. ed.

8-

6-

4-

2-

I, отн. ед.

16- в) -10 -8 -6 -4 -2   0   2   4   6

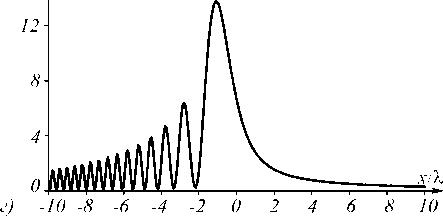
Рис. 3. Распределение интенсивности 2D ПП-пучка, рассчитанное BPM-методом: сечение интенсивности вдоль оси x при z = 0 (a), интенсивность в плоскости Oxz (негатив) (б), сечения интенсивности вдоль оси x при z = 0 (в)(увеличенная картинка (а)) и при z = 75 λ /8 (г)

В заключение данного раздела заметим, что в отличие от трёхмерных пучков комплексные амплитуды двух 2D ПП-пучков с параметрами x ₀₁ и x ₀₂ не ортогональны.

Заключение

В работе получены следующие результаты:

– получено новое решение параксиального уравнения Гельмгольца (уравнения типа Шрёдингера), описывающее трёхпараметрическое семейство структурно-устойчивых трёхмерных половинных пучков Пирси (уравнения (4), (5));

– показано, что полный пучок Пирси из [8] является суммой двух симметричных половинных пучков Пирси первого порядка (уравнение (7)); с помощью линейной комбинации из двух симметричных половинных пучков Пирси с разными амплитудами можно формировать новые структурно-устойчивые пучки, которые не будут ни полными пучками Пирси [8], ни половинными пучками Пирси;

– получена формула для амплитуды углового спектра плоских волн трёхмерных половинных пучков Пирси (уравнение (6)); амплитуда спектра отлична от нуля на половине параболы;

– получено условие ортогональности комплексных амплитуд трёхмерных половинных пучков Пирси: ортогональны половинные пучки Пирси, Фурье-спектр которых лежит на непересекающихся параболах; установлено, что двумерные пучки Пирси не ортогональны;

– получено решение двумерного параксиального уравнения Гельмгольца, описывающее двумерный аналог структурно-устойчивых половинных пучков Пирси (уравнения (9), (11));

– показано, что двумерный половинный пучок Пирси, как и трёхмерный, обладает свойством автофокусировки, а также ускоряющейся траекторией до фокальной плоскости (рис. 3 б ).

Работа выполнена при поддержке грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ 13-07-97008 и 14-07-31092.