Структурное моделирование процессов теплопроводности с замыканием распределенных обратных связей

При расчетах и моделировании реальных объектов и систем не всегда удается пренебречь их распределенностью в пространстве. Построение распределенных моделей объектов само по себе является достаточно сложной задачей, решение которой привело к широкому распространению приближенных методов моделирования объектов с распределенными параметрами (ОРП) [1.. .3]. При этом преобладающей тенденцией является стремление к построению эквивалентных сосредоточенных моделей, поскольку с их помощью можно описать ОРП простой сосредоточенной моделью с любой желаемой точностью и с сохранением ее аналитических свойств, а после аппроксимации применить привычный фундаментальный математический аппарат теории автоматического управления.

Решим в общем виде краевую задачу параболического типа методом Гринберга, или обобщенным методом Фурье [4] (при решении были использованы обозначения [5]). Для упрощения возьмем одномерную тепловую задачу.

Пусть имеем распределенную краевую задачу, описывающую процессы диффузии, с постоянными по времени коэффициентами, решение которой T = T ( x. t ) удовлетворяет неоднородному дифференциальному уравнению (ДУ) в частных производных:

L x { ^T } ⁺ M, { T } = F ( ^x . t ) , ^{x G} ( c . d ] , t ^G [ °, ~ ) , где L x { T } и M_t { T } - линейные дифференциальные операторы:

а по переменной t - начальным условиям

^{T ( x} . t ) _t =

= ^Пф ( ^x ) , v T ( x . t ) d t ^v '

= TM x ) ^,

t =0

где T ₀ и T - масштабные коэффициенты.

Пусть функцию внутреннего воздействия можно представить в виде F ( x.t ) = а ( t ) в ( x ) ,где в ( x ) -известная аналитическая функция пространственного распределения входного воздействия, фиксированная на все время моделирования; функция а ( t ) - времязависимый компонент воздействия, который может иметь любой вид и

быть заранее неизвестный. Таким образом, уравнение диффузии запишется в виде

Lx {T} + Mt {T }=а( t )р( x).

Преобразуем по Лапласу исходные уравнения задачи по переменной t . Получим L x { T } + M s { T } = А ( s Ш x ) , или, с учетом вида выражения для оператора M_t { T } ,

L 1 Mil = A ^-T + B — + CT ^ >  T(As² + Bs + C ) —

I t ^{{ }} d t²         d t         |         ⁽                  )

- Ds ■ T m ( x ) — E ■ T ° 9 ( x ) =

= ^T ■ M s ( s )^{- T} i D s -V ( ^x )^{- T} ° E "ф ( ^x ) . L x { T } + T ■ M s ( s ) = A ( s ) P ( x ) +

+ TDs ■ m ( x ) + T ° E ■ ф ( x ) .

Lx {T} = \ г r ( x)^dx

p ( ^x ) I ^- q ( ^x ) ■ ^T d x )

M {T } = a Ц- + B ^T + CT ^{t { }} d t¹       d t         ’

у которых функции p ( x ) , p ‘ ( x ) , q ( x ) , r ( x ) непрерывны на интервале [ c, d ] , p ( x ) > ° , r ( x ) > ° .

Кроме того, функция T = T ( x. t ) удовлетворяет по переменной x граничным условиям (ГУ) одного из следующих типов:

- ГУ I рода

^{T ( x} , t )| x = c =Y c ⁽ t ) , ^{T ( x} , t )| x = _d = Y d ⁽ t ) ;

- ГУ II рода

^T ( x.t ) =Y c ( t ).£ T ( x.t ) =Y d ( t ) ; x = ^c                            x = d

-ГУШ-ГУрода dxT(x.t)-hc • T(x.t)

■^ T ( x . t ) - h d • T ( x . t ) d x

= Y c ⁽ t ) ,

, =

= Yd (t)

Рассмотрим соответствующую задачу Штурма-Лиувилля (разложение решения исходного однородного уравнения в ряд по собственным функциям по координате x с нулевыми ГУ) и найдем нетривиальные решения уравнения L x { X ( x ) } +X X ( x ) = 0 , удовлетворяющие нулевым ГУ. Запишем L x { T } в явном виде:

r ( x x)

p ( x ) X ( x ) |- q ( x ) ■ X ( x )

+ X X ( x ) = 0 ,

или ( pX ‘ ) + ( % r - q ) X = 0 ,           (2)

удовлетворяющее соответствующим нулевым граничным условиям. При сделанных предположениях задача регулярна [4; 6] и имеет дискретный спектр собственных значений % n . Пусть X = X n ( x ) -собственные функции поставленной задачи. Найдем решение задачи по методу Гринберга [4] в виде

Cn (s ) =

и

T ( x. s ) = Z Cn ( s ) Xn ( x ), n=1

d

J r (x) T (x. s) Xn (x) dx

c

Tn (s )

IIXn (x )|I'            IXn (x )|Г

Изображение времязависимого коэффициента T n ( s ) получим по исходному уравнению задачи. Умножим выражение (1) на r ( x ) X n ( x ) и проинтегрируем его по x :

d ( XГ д ( . д T

J Xn (x) д~1 Р(x).> J        дx       дx

c

^^^^^^s

q ( x ) • T dx +

T n M s ( s ) -% T = A ( s ) ₽ . + sT 1 D V . + T o E ф . - G n ( s ) .

В [4] показано, что функция G n ( s ) имеет вид ^Gn ( ^s ) = ^ю n ^г c ( ^s ) + ^ n ^г d ( ^s ) , ^где ^коэ^ффиц^ие^нты ю . ^и ^ . находятся в зависимости от вида граничных условий за

d

+ J T • M s ( s ) r ( x ) X n ( x ) dx =

c

d

= J A ( s ) в ( x ) r ( x ) X n ( x ) dx +

c

d

+ J Ds • у ( x ) r ( x ) X_n ( x ) dx +

c

d

+ J E ^ф ( x ) r ( x ) X_n ( x ) dx .

Взяв по частям первый интеграл, имеем [4]:

дачи.

Таким образом, получаем следующее решение:

Tn (s ) =

A(s )вn + sTDVn + T0EФn -юnГc (s )+^nГd (s ) Ms (s)-%n

Учитывая C_n ( s ) , получим

^

T (x, s ) = ^

n =

T n ⁽ s ) X " ⁽ x ) = ^A( s )^B( x . s ) + T v ( x , s ) +

II x. (x 1

" ^дГ - X. nn

G n ( s )

+

c

+ T o Ф ( x,s ) -Г c ( s ) Q ( x,s ) +Г d ( s ) E ( x,s ) .

Это выражение может быть представлено в виде структурной схемы (рис. 1).

Решение T ( x, s ) получено путем подстановки интересующих значений координаты x и дальнейшего обратного преобразования Лапласа аналитически или численно. В статье [7] приведена структурная схема задачи нагрева бесконечного цилиндра, результаты моделирования и их сравнение с известными аналитическими решениями из монографии [5].

Представленный выше вид решения (2) и структурную схему (см. рис. 1) возможно получить и другими методами. Например, в [1] приведено доказательство правомерности такого подхода с использованием метода функций Грина. Там же введено понятие переходного х-блока с сосредоточенным управлением, если решение получено для всей области объекта, и переходного x ^ -блока, если решение получено для конкретных значений точек x = x k .

Более сложная ситуация возникает, если убрать допущение об известном виде пространственно-зависимой

d                         d-

J ( pX n ) - qX n ^dx + M s ( s ) J ^T • r ^Xn^dx =

d

d

+

1 ^L4 4 4 2 4 4 ^3

=-% С • X n ="% . T

d

c

T

n

d

A (s) J в (x) rXndx + TDs J v(x) rXndx + cc в n                            V n

d

+ T _o E J ф ( x ) rX n dx,

_                              Фn где Tn (s), %., в., у., ф. - функции координаты учетом (2) получаем уравнение для Tn (s):

x .C

Начальные условия

Внутреннее управление

Граничное управление

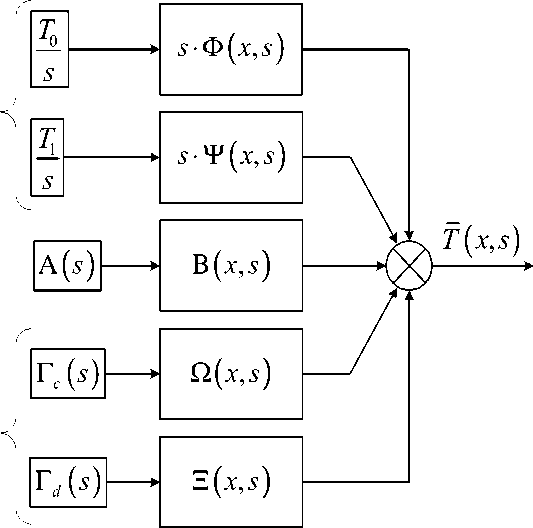
Рис. 1. Структурная схема решения распределений задачи без получения фундаментального решения: s - оператор Лапласа; T ( x, s ) - изображение решения исходного ДУ процессов диффузии

составляющей в ( x ) функции внутреннего управления. В этом случае решение может быть получено в виде пространственной композиции, представляющей собой операцию пространственного интегрирования произведения функции Грина и в ( x ) в пределах области объекта [1]. Эта операция сама по себе достаточно сложная, редко может быть решена аналитически, мало пригодна для инженерных расчетов и имитационного моделирования в пакетах прикладных программ, а затраты вычислительных ресурсов в этом случае сравнимы с методом конечных элементов.

В монографии [3] приведен инженерный метод имитационного моделирования, основанный на приближенном вычислении интеграла пространственной композиции. Для этого в области объекта выделяют точки или линии приложения воздействия (входы), интерполирующие функцию в ( x ) . Далее подбирают некоторые весовые коэффициенты, при которых сумма функций отклика от приложенных в выбранных точках воздействий повторяет точное решение распределенной задачи. Точность решения определяется размерностью модели по входу а функции отклика получают, интегрируя функцию Грина заранее.

Используя описанный выше метод получения структурной схемы распределенной задачи без получения фундаментального решения, можно получить решение даже при изменяющейся во времени зависимости в ( x ) . Если функция внутреннего управления представлена в виде конечной суммы, то вследствие свойства линейности уравнения диффузии решение уравнения (3) будет иметь вид

T(x,5) = ХАk (5)Вk (x,5) + TiW(x,5) + k

+ T Ф ( x, 5 ) —Г c ( 5 ) Q ( x, 5 ) + Г d ( 5 ) E ( x, 5 ) .

Оно может быть представлено в виде структурной схемы (см. рис. 1), в которой функция внутреннего управления будет иметь k входов.

Удобный способ такой аппроксимации функции внутреннего управления - это приближение управления полиномиальной зависимостью по координате с времяза-

N висимыми коэффициентами F(x,t) = Z«k (t)xk.

k =0

Точность решения будет определяться только точностью аппроксимации, т. е. порядком многочлена к.

В любом случае при неизвестном заранее управлении должен производиться такой подбор коэффициентов ak (t), чтобы F(x,t) = ^аk (t)Pk (x) ,где вk (t) может k быть любой функцией. В модели должен быть реализован блок подбора ak (t), например с использованием методов Гаусса-Ньютона, Левенберга-Марквардта или модифицированных методов для аппроксимации полиномами.

Таким же образом через блок подбора a _k ( t ) может быть заведена распределенная обратная связь. Используя теорему о непрерывной зависимости решения от параметров уравнения и правой части, можно сократить время вычислений, если производить поиск коэффициентов на z-м шаге a _k ( t , ) в окрестности значений предыдущего шага интегрирования a _k ( t , _{- 1} ) .

Пусть функция внутреннего тепловыделения имеет вид

F (x, t ) = N {U (t )• V (x), T (x, t)}, где N - некоторый оператор; U(t)• V(x) - внешний фактор тепловыделения; T(x, t) -температура объекта. И пусть пространственную составляющую функции F (x, t) можно интерполировать многочленом первого порядка F (x, t) = a (t) x + b (t), где а и b - коэффициенты, зависящие от ии Т, т. е. ии Тсами имеют линейный вид зависимости по координате. Тогда структурная схема объекта с замкнутой по T (x, t) обратной связью будет иметь вид, показанный на рис. 2.

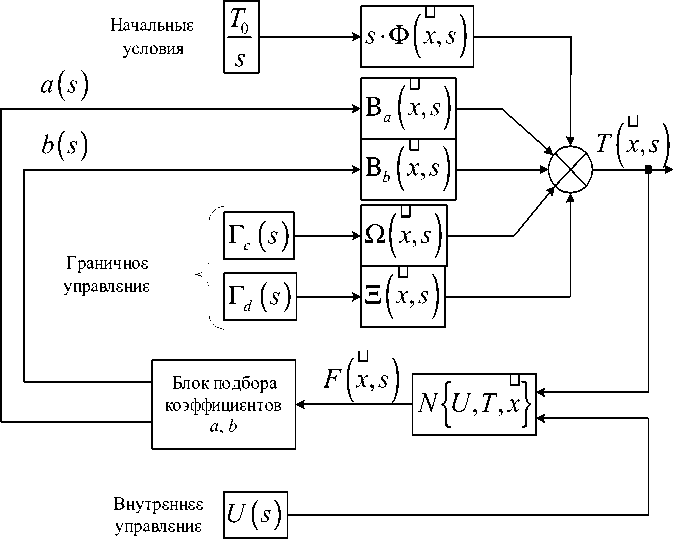
Рис. 2. Структурная схема объекта замкнутой по Т(х, f) обратной связью

В случае когда пространственная составляющая функции внутреннего тепловыделения имеет простой вид, алгоритм блока подбора коэффициентов можно записать аналитически и объединить его с оператором N в одну нелинейность. Помимо этого, разумным выбором координаты и количества точек x функции F ( x,s ) ,т. е.переходом от бесконечномерного распределения x к вектору x = [ x 1 , x ₂,К , x m ] ,по которым производится аппроксимация, можно существенно сократить размерность задачи, сохранив точность и быстроту решения.

Таким образом, сделаем следующие выводы:

• -    автором предложен метод, позволяющий рассчитывать передаточные функции объектов с распределенными параметрами, описываемые уравнениями диффузии с постоянными коэффициентами при входных воздействиях, приближаемых линейным оператором время-и пространственно-зависимой компоненты. Метод основан на решении задачи в области изображений без получения фундаментального решения, с допущением об известном характере пространственного распределения функции управляющего воздействия;

• -    представлен вариант замыкания распределенной обратной связи, основанный на представлении поля решения линейным оператором время- и пространственно-зависимой компоненты;

• -    предложенный метод позволяет существенно уменьшить размерность задачи, обеспечивает высокую точность моделирования при низких затратах вычислительных ресурсов, допускает простую реализацию в пакетах имитационного моделирования;

• -    модель объекта с распределенными параметрами может быть получена в аналитической форме, что по

зволяет производить анализ системы при переменных коэффициентах дифференциального уравнения.