Структурное проектирование информационно-технологической подсистемы многоцелевой оптимизации управления качеством электроснабжения

Стратегическим направлением развития электроэнергетики России, сформулированным в «Основных направлениях реформирования электроэнергетики Российской Федерации», определено создание эффективной системы управления функционированием и планированием развития энергосистем, объединённых энергосистем и ЕЭС России, включая управление на рынке мощности и энергии [1].

Проблема управления качеством электроснабжения (УКЭС) рассматривается в мировой практике в составе понятия «качество электроснабжения» (“power quality”), объединяющего в себе две обширные проблемы обеспечения электромагнитной совместимости и бесперебойности (надёжности) электроснабжения [2]. Комплексному решению проблемы УКЭС способствует развитие новых информационных технологий принятия решений и их синтез в существующие или вновь создаваемые технологические подсистемы АСУ ЭЭС (АСДУ, АСУ КЭ, АСКУЭ и др.) [3-5].

Формулируется задача структурного проектирования подсистемы многоцелевой оптимизации (МО) УКЭС в составе АСДУ ЭЭС в следующем виде [6]. Для заданного объекта управ

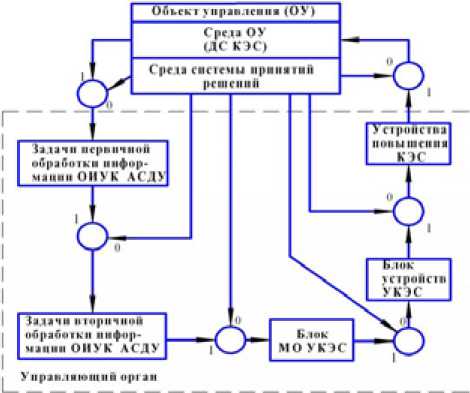
Рис. 1. Подсистема МО УКЭС ления (ОУ) и среды его функционирования, определяемой динамическим состоянием качества электроснабжения (ДС КЭС), спроектировать на базе типового комплекса задач ОИУК АСДУ управляющий орган принятия решений МО УКЭС, обеспечивающий с помощью среды принятия решений алгоритмический учёт основного комплекса кибернетических свойств ОУ Управляющий орган принятия решений в составе технологической АСУ ЭЭС вместе с ОУ образуют сложный системный объект количественного и качественного исследования – информационнотехнологическую подсистему МО УКЭС (рис.1).

Проектирование подсистемы МО УКЭС производится на основе структуралистского системного подхода по Дж. Клиру с использованием архитектуры экспертной системы, представленной универсальным решателем системных задач (УРСЗ) [7]. Выделенная подсистема рассматривается в ортогональной системе координат двух фундаментальных критериев различия:

• а)    подсистема базируется на определенных типах элементов;

• б)    подсистема базируется на определенных типах отношений.

В соответствии с критерием а) элементами подсистемы назначаются типовые блоки комплексов задач ОИУК АСДУ (сбор, хранение, передача, обработка информации; контроль, анализ состояния и режимов работы ЭЭС и др.), укрупненно сформулированные как задачи первичной и вторичной обработки информации АСДУ [8]. Критерий б) характеризуется типами отношений между элементами подсистемы, выраженными через проявления в них комплекса кибернетических свойств ОУ.

Применительно к подсистеме МО УКЭС направленная алгоритмическая последовательность комплексов задач ОИУК АСДУ представляется в виде множества элементов Bj баз объекта вj: в1 – задачи сбора и первичной обработки информации МО УКЭС; в2 – задачи учёта, контроля состояния и неэкстремального анализа режимов КЭС; в3 - задачи формирования критериев и целевых условий оптимизации; в4 – задачи расчётов компромиссных параметров МО УКЭС; в5 – задачи расчётов прогнозных компромиссных параметров МО УКЭС; в6- задачи расчётов межсистемных компромиссных параметров МО УКЭС; в7 - за-– 195 – дачи оценки эффективности компромиссного УКЭС. Отношения элементов подсистемы МО УКЭС в управляющем органе принятия решений характеризуются множествами алгоритмических проявлений Аi учитываемых свойств ОУ аi, которые генерируются средой системы принятия решений (рис.1): а1 – управляемость; а2 – динамичность; а3 – иерархичность; а4 – неопределённость; а5 – многокритериальность; а6 – адаптивность; а7 – устойчивость; а8 – экономическая эффективность.

Моделирование подсистемы МО УКЭС для заданных элементов и их свойств производится по уровням эпистемологической иерархии:

уровень 0 – исходная система;

уровень 1 – система данных;

уровень 2 – порождающая система;

уровень 3 – структурированная система.

Уровни эпистемологической иерархии отличаются друг от друга уровнем знаний по отношению к переменным, представляющим исследуемую исходную систему. В системах более высоких эпистемологических уровней используются все знания соответствующих систем более низких уровней иерархии, а также содержатся дополнительные знания, ранее недоступные более низким уровням иерархии.

Исходная система является источником эмпирических данных, т.е. источником описания на языке УРСЗ абстрактных представлений об объекте. Она служит также источником интерпретации абстрактных данных, которые определяются пользователем или выводятся с помощью УРСЗ.

Уравнение исходной системы записывается в виде

S = (O, İ, I, Q, ξ),(1)

где O, İ, I – уравнения примитивных систем:

O – уравнение системы объекта о = ({«/, Ai\ig Nn},вj,Bj\j G Nm});

İ – уравнение конкретной представляющей системы

I = ({vi, V'V g Nn} кj, Wi\j g Nm});

I – уравнение общей представляющей системы

I=({ vi, VVG Nn} к, Wj\j GNm});

Q, $ - уравнения отношений между примитивными системами (2) - (4):

^Q = \ A.,V.,o\^ ^G №г,°_Л ^ V. ^} ,

{Bj, Wj,j-G Nm, ^.; Bj^Wj\;

• I.

^ = V . , V_r e\i g Nn, e :V -> V . } , i i i ii i

Таблица 1. Нейтральная система данных свойства a i

Ба ш в1

*-

e.

Пчре.метры *■, *иож<чтв.1 II'

5

1

J

6

ч" ; в

В * 5

>

в

fl

fl

fl

ft

fl

J

ft

ft

fl

fl

ft

fl

2

Я

у

I

у

fl

ft

1

!

6

/

/

9

i

4

ft

1

й

I

i

5

0

8

у

I

/

f

6

6

*-

6

h

1

ft

7

0

ft

ft

fl

ft

1

f

0

Wi' j .W j e j jj g Nm, s /Wj ^ W j } .

Уравнение (1) отражает семантические аспекты исходной системы. С абстрагированием связаны функции оi, mj, ei-: Vi ^ Vi , 5 -1: Wj ^ Wj. Конкретизация характеризуется функциями ei, 5j и разбиениями оi-= Аi / оi, mj-= Bj / mj. Прагматические аспекты уравнения исходной системы вводятся на дометодологическом уровне формулирования цели исследования и огра- ничений на определённые действия.

Упрощение операций с уравнениями примитивных систем O, İ, I достигается тем, что свойствам a( еNn) соответствуют переменные v^v^ а базам вj(еNm) соответствуют параметры WjWj. Принимается также, что чёткий полный канал наблюдения Q между системой объекта и общей представляющей системой состоит из отдельных каналов наблюдения, по одному для каждого свойства аi и базы вj.

Уравнение (1) описывает нейтральную систему данных с семантикой SD = (S, d), где d: W →V . Система данных для канала наблюдения свойства а1 подсистемы МО УКЭС пред- ставлена в табл. 1.

Преобразование нейтральной системы S в направленный аналог Ŝ производится по- сле введения понятий среды системы, входных и выходных переменных, удовлетворяющих утверждению “если x, то y”. Направленная система с поведением представляется в виде уравнения

F iВ = (I i , M i , f iB ) ,

где M_i – маска свойства а_i ; f_iB – функция поведения.

С помощью функции поведения f iB : С ij →{0,1} задаётся параметрически инвариантное ограничение на множество переменных v_i уравнения общей представляющей системы (4).

Система с поведением (7) может принять порождающий характер через представление маски M_i в порождающую маску направленной системы в виде

А

М iG = (M i , M ie ; M ig , M ) ,                                   (8)

ig где Mie – подмаска, определяющая среду системы; Mig – подмаска порождаемых переменных;

M – подмаска порождающих переменных.

ig

Направленная система с поведением (7) преобразуется в порождающую направленную систему с поведением

А  АЛА

∧ где f iGB : Ес Gi • Gi^[0, 1] — порождающая функция поведения, соответствующая структуре

А маски МiG.

Нормализованное значение порождаемой нечёткости направленной системы с поведением, генерируемой заданной средой системы и порождающими переменными определяется по формуле

HH ( GE i • G i ) =

^H i (C ij ) — H i (E i • G i ) log₂ (G i )

Здесь H i – показатель нечёткости направленной системы с поведением, выраженный через вероятностное представление функции поведения порождающих и порождаемых нечётких данных.

N (C ) ij     i j

fiR(CH ) =                ’ iB ij         N (C )

ij ij a e C ij ij где Cij – подмножества состояний переменных.

Практические расчёты показали, что наименьшей порождаемой нечётностью обладает структура моделируемой подсистемы МО УКЭС, представленная свойством многокритериаль-ности ( а₅ ) как наиболее структурно разработанная ( H ^( G₅\E 5 • G 5 ) = 0 , 29 ) .

Описание подсистемы МО УКЭС ST-функциями учёта отдельных свойств a i удовлетворяет целевым критериям структурной оптимизации с заданными структурными ограничениями. В этом случае проектируемая подсистема МО УКЭС рассматривается как обобщённая система с поведением. Взаимоотношения между обобщённой системой и разными множествами её подсистем (ST-функциями) сводятся к задаче идентификации вариантов множества подсистем по некоторому показателю, характерному только для этой обобщённой системы. Задача идентификации вариантов подсистем, вытекающая из условия непротиворечивости обобщённой системы МО УКЭС, решается в два этапа:

• 1)    формируется реконструктивное семейство в виде множества всех структурированных подсистем;

• 2)    производится выбор из реконструктивного семейства такой подсистемы, которая задаёт в определённом смысле лучшую гипотезу относительно реальной обобщённой системы с поведением.

Размер реконструктивного семейства оценивается показателем

R^^F = П [ 1 + f^SF(c) ] , с е A^{L           J}

Таблица 2. Реконструктивное семейство обобщённой системы с поведением

v1 v2 v3 v4 fiSF 1 2 3 4 5 6 7 8 С1 0 0 1 1 0,059 0,091 0,182 0,077 0,035 0,083 0,083 0,071 С2 0 1 1 0 0,059 0,182 0,091 0,077 0,035 0,083 0,083 0,071 С3 1 1 0 0 0,176 0,091 0,091 0,077 0,07 0,083 0,083 0,071 С4 0 1 0 1 0,176 0,091 0,182 0,231 0,31 0,166 0,333 0,142 С5 1 0 1 0 0,176 0,091 0,182 0,231 0,172 0,166 0,166 0,071 С6 1 0 0 1 0,176 0,182 0,182 0,231 0,172 0,25 0,166 0,142 С7 0 0 2 1 0,176 0,273 0,091 0,077 0,207 0,166 0,083 0,429 где f SF(c) – максимальный элемент реконструктивного семейства из множества возможных преобразований входных переменных в выходные (c ∈ A). Показатель реконструктивной нечёткости обобщённой системы определяется как

U sf = log 2 П , 1 + f^SF(c) ] - £ log₂ [ 1 + f^SF(c) ] ;                  (13)

c e A

⁰ ^ U SF ^ И •

Степень идентифицируемости альтернативных обобщённых систем, сопоставимых с заданным реконструктивным семейством, определяется коэффициентом идентифицируемости

U

I SF = ¹ -      ^; 0 * I SF * ^{1                         (1}4)

Для заданной реконструктивной нечётности всего множества возможных преобразований входных переменных в выходные |C| = 16 реконструктивная нечёткость подсистемы МО УКЭС с лучшим набором свойств f ^SF равна U ^* _SF = 2,245. Коэффициент идентифицируемости системы равен I* SF = 0,86.

Задача реконструкции несмещённой системы f ^h рассматривается как требование определения набора её свойств а_i в заданном реконструктивном семействе. Каждый из наборов свойств считается гипотетической реконструкцией обобщённой системы в целом. Близость сопоставимых систем, представленных лучшим набором свойств f ^* и несмещённой реконструкцией f ^h , определяется разностью информации, содержащейся в их функциях поведения и представляется как потеря информации при замене f ^* на множество её проекций f ^h . Мера потери информации в информационной теории систем называется информационным расстоянием, которое применительно к порождающей направленной системе с поведением определяется по формуле [8]

D G (f'’ fh ) = dG £ f ( 8 2  g G G

) у fTgig ^-iog 2 f(glgL , geG         f (glg )

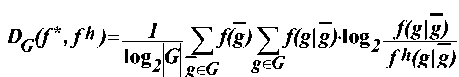
Таблица 3. Информационное расстояние D G (f *f )•10^-8

D 1	D 2	D 3	D 4	D 5	D 6	D 7	D 8
798	939	948	672	516	713	709	647

Сред» ОУ

II роек nipt см а я система

Подсистема МО У КЭС

Среда подсистемы МО У КЭС

НаправленпаяcncieMa

Алгоритмические модели МО

Первичная информация У КЭС

Случайные процессы

Методология МО

Д и и а м и ч ССКОС сое t «я и и с качиста элекiроснабження

У чет. кон । роль и авали! режимов ЭЭС

II ронедх ры

|Шк’алпр<М1явис|

М еж систем пая коорднна-

рсшсиип МО Подходы Полет- Игро-

Норма. Швеция

Способы формирования и сужения псходио! о множества алктернатв УКЭС

Неивиси-маяон in-ми |аиия по к ри 1срням

■ельная ирог-нотная информация

Ошнми-иппя про! ноia

Отбрасывай не нариэнгон ре in с и ин

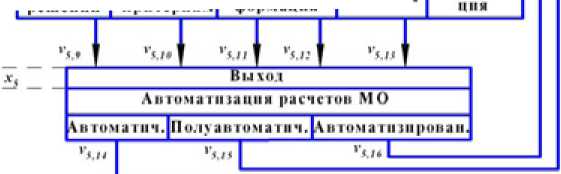
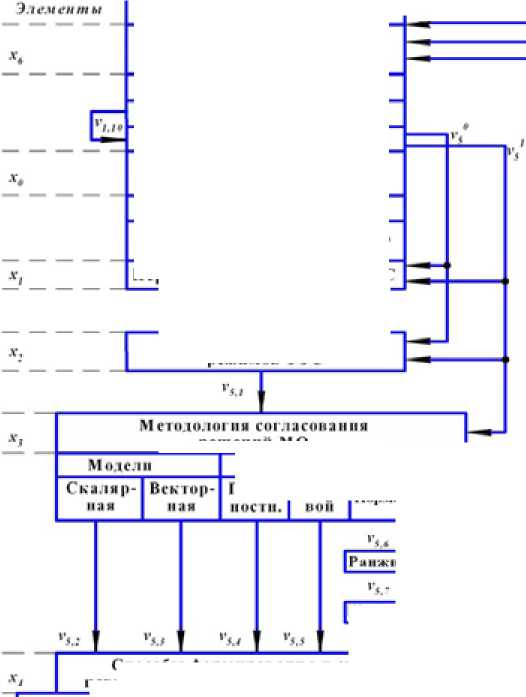
Рис. 2. Структурная схема свойства многокритериальности

0 ^ ^DG^f* ,f ^h) ^ ¹ .

В табл. 3 приведены результаты расчётов информационного расстояния между обобщённой системой с поведением, спроектированной по гипотезе h (подсистема МО УКЭС характеризуется свойствами a_i ) и смещённой обобщённой системой с поведением, представленной лучшими (максимальными) элементами реконструктивного семейства табл. 2

Расчёты производились для полного множества состояний выборочных переменных |G| = 119. Из табл. 3 видно, что в заданном реконструктивном семействе наименьшим информационным расстоянием обладает проекция обобщённой системы с поведением, представленная свойством многокритериальности Dg(( ,f^)= 0,516 • 10—8 . Реконструктивная нечёткость данной проекции U5„ =1,316, что значительно меньше реконструктивной нечёткости SF обобщённой системы с лучшим набором свойств USf < U*sf = 2,245. Коэффициент идентифицируемости свойства многокритериальности получается выше, чем у обобщённой системы /5 = 0,917 > ISF = 0,86, что характеризует наибольшую разработанность структуры данного SF       SF свойства в обобщённой системе с поведением.

На рис. 2 приведена структурная схема свойства многокритериальности а 5 проектируемой подсистемы МО УКЭС.

Разработанная структура в последующем может быть использована для разработки адаптивных функциональных алгоритмических моделей МО УКЭС [3].

Выводы

• 1.    Проектирование информационно-технологической подсистемы МО УКЭС производится на элементной и информационной базе существующих ОИУК АСДУ ЭЭС. Наиболее полные сведения о проектируемой подсистеме МО УКЭС содержатся в структурах алгоритмического учёта кибернетических свойств ОУ.

• 2.    Использование структуралистского системного подхода на основе УРСЗ обеспечивает управляемость процесса проектирования сложного системного объекта и автоматизацию проектных решений.

• 3.    Создание адаптивных структур, характеризующих отдельные свойства ОУ, позволяет проектировщику осуществлять направленный контроль и количественную оценку сравниваемых вариантов структур.