Структурное прогнозирование физико-механических характеристик оксидной пенокерамики

сжимающих напряжений, в то время как в реальной макроструктуре определяющими являются изгибные напряжения с предельными значениями, в не сколько раз меньшими, чем предельные напряжения сжатия.

Цель работы: установление зависимости между величиной сжимающей образец нагрузки и локальными напряжениями в структурных элементах ячейки с последующим определением эффективных значений разрушающего напряжения (предела прочности) и модуля упругости в зависимости от аналогичных параметров компактного материала.

Исследуемый высокопористый материал моделировался в виде периодической структуры, ячейки которой представляют собой тетра-каидодекаэдры (рис. 1).

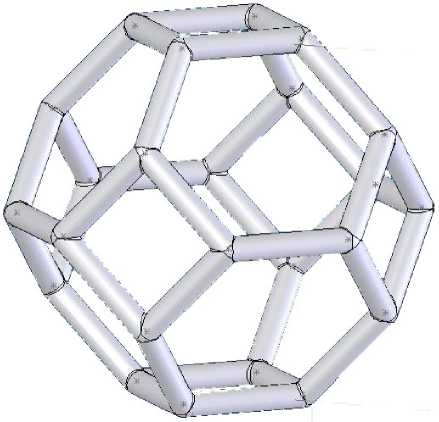
Рис. 1. Твердотельная модель единичной ячейки пенокерамики

Построение геометрии ячейки выполнялось в системе твердотельного моделирования Solid Works. Представленная на рис. 1 структура образована совокупностью восьми равных между собой плоских шестигранников и шести квадратов с равными по величине размерами ребер. Геометрические размеры данной структуры зависят только от размера ребра, что позволяет на начальном этапе моделировать ячейку произвольного размера, а потом масштабировать ее до необходимых величин. Для установления связи между пористостью и геометрическими параметрами структурных элементов ячейки была получена приближенная аналитическая зависимость:

П=1-k(d/D)2, (1)

где k – коэффициент пропорциональности для данной конструкции равный 6,7; d – диаметр сечения перемычки; D – диаметр ячейки.

Зависимость (1) получена в предположении, что каркас пенокерамики сформирован из цилиндров постоянного поперечного сечения по всей их длине, хотя, как видно из рис.1, в геометрической модели каркаса тетракисдоде-каэдра в узлах конструкции наблюдается подрезание торцов перемычек. Для оценки точности формулы (1) были проведены расчеты по твердотельной модели для ячейки с диаметром 1,41 мм, сравнение результатов которых с результатами расчетов по формуле (1) представлено в табл. 1. Из таблицы 1 следует, что для пористости 95-97% погрешность вычисления по формуле (1) близка к нулю, в то время как снижение пористости до 75% сопровождается ростом погрешности до 15%.

Таблица 1. Расчетные значения диаметра перемычки ячейки пенокерамики

Пористость, %	Диаметр перемычки d, мм по формуле (1)	Диаметр перемычки d, мм по твердотельной модели
75	0,268	0,317
80	0,240	0,277
85	0,208	0,236
90	0,170	0,188
95	0,128	0,129
97	0,100	0,100

Создание параметрической твердотельной модели ячейки в виде тетракаидодекаэдра, определение координат узлов ячейки и установление функциональной зависимости пористости от размера ячейки и диаметра сечения перемычки позволило перейти к определению эффективных модуля упругости и предела прочности пенокерамики. Расчетная схема для определения эффективных механических характеристик материала, представленная на рис. 2, включала структурный элемент из 27 ячеек, к верхним узлам которого прикладывалась сжимающая нагрузка.

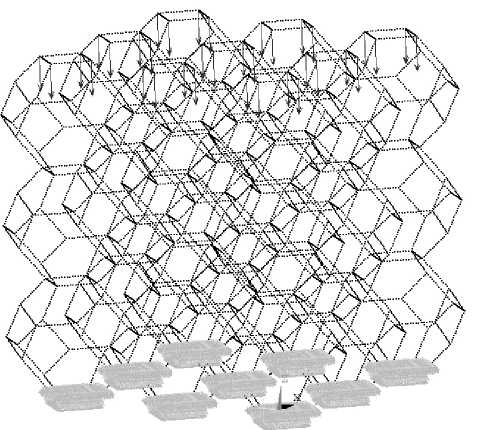
Рис. 2. Расчетная схема нагружения модели высокопористого ячеистого материала в программном комплексе ANSIS

Представленная схема позволяет в последующих расчетах прочностных характеристик рассматривать отклик на внешнее воздействие центральной ячейки конструкции. В процессе вывода результатов расчета напряженного состояния структурных элементов остальные 26 ячеек, окружающие центральную ячейку, исключаются из рассмотрения для устранения влияния краевых эффектов. Вычисление отклика конструкции на внешнее воздействие производилось в программном комплексе МКЭ ANSIS. Построенная система ячеек представлялась как балочная конструкция, схема которой имитирует одноосное сжатие. Граничные условия для данной схемы нагружения предполагали фиксацию всех перемещений узлов конструкции, лежащих в основании, и приложение к верхней плоскости конструкции сжимающего давления величиной 1 МПа. Приложение нагрузки к узловым точкам связано с необходимостью исключения дополнительных изгибающих моментов в перемычках, лежащих в верхней плоскости структурного элемента, возникающих в случае приложения распределенной нагрузки. Для создания сетки конечных элементов использовался балочный элемент с конечными деформациями BEAM 188. Элемент построен на основе балки

Тимошенко и пригоден для моделирования прямых балочных конструкций, имеющих умеренное соотношение длины и толщины. В элементе учитываются эффекты касательных (сдвиговых) напряжений. Разбиение на конечные элементы проводилось с заданием числа элементов на линию. Для получения приемлемых по точности результатов экспериментальным путем установлено достаточное число конечных элементов, равное 15.

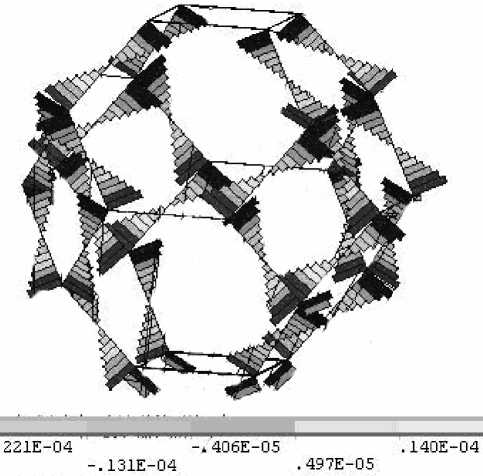
а)

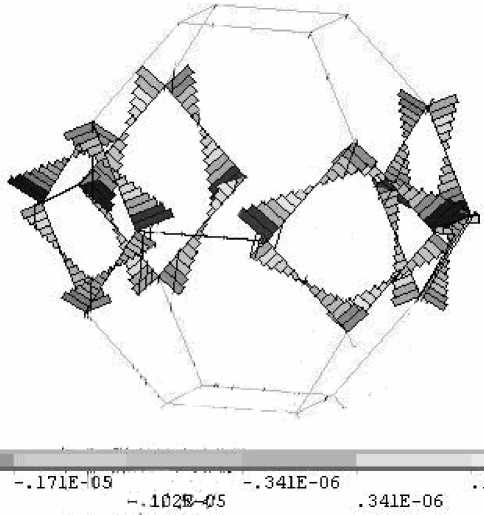
б)

Рис. 3. Эпюры изгибающих моментов центральной ячейки конструкции из оксида алюминия Al2O3: а) – относительно оси y конечных элементов; б) – относительно оси z конечных элементов

Рис. 4. Распределение эквивалентных напряжений по Мизесу в центральной ячейке конструкции из оксида алюминия Al 2 O 3 под действием внешней разрушающей нагрузки

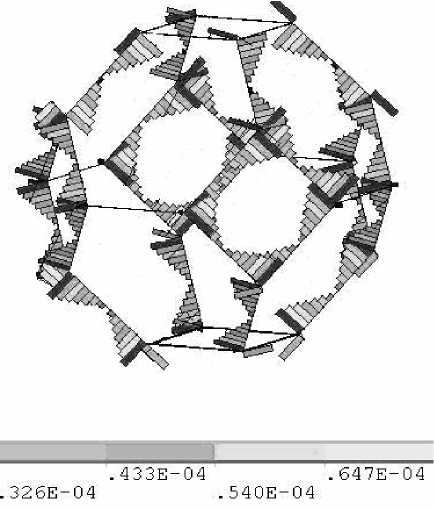
Рис. 5. Эпюры суммарных изгибающих моментов на перемычках каркаса высокопористого электрофарфора, нагруженного внешней сжимающей нагрузкой

На рис. 3, а,б представлены эпюры изгибающих моментов относительно осей y, z конечных элементов (ось x совпадает с осью перемычки) для пористого оксида алюминия

Al 2 O 3 со следующими физико-механическими свойствами материала каркаса: модуль упругости E=400 ГПа; коэффициент Пуассона µ=0,2; предельные напряжения на изгиб [σ и ]=200 МПа.

Распределение эквивалентных напряжений центральной ячейки конструкции из оксида алюминия Al 2 O 3 под действием внешней разрушающей нагрузки представлено на рис. 4. На рис. 5 представлены результаты расчета суммарных изгибающих моментов для ячейки каркаса высокопористого электрофарфора.

По данной методике были рассчитаны эффективные механические характеристики прочности, модуля упругости, а также перемещения плоскости приложения нагрузки при сжатии для высокопористых оксида алюминия с указанными выше свойствами материала основы и для электрофарфора со следующими характеристиками материала каркаса: E=70 ГПа; µ=0,2; [σи] = 100 МПа (табл. 2).

Результаты сравнения расчетной и экспериментальной прочности [2] для высокопористых оксида алюминия и электрофарфора при различных значениях пористости приведены на рис. 5.

Таблица 2. Результаты расчета физико-механических характеристик высокопористых керамических материалов

Пористость, %	Диаметр сечения перемычки, мм	Внешнее разрушающее давление, МПа		Перемещения плоскости приложения нагрузки, мм		Приведенный модуль упругости, ГПа
		Al2O3	электрофарфор	Al2O3	электрофарфор	Al2O3	электрофарфор
75	0,268	3,920	1,954	0,577.10-3	0,330.10-2	7,353	1,954
80	0,240	2,805	1,404	0,821.10-3	0,467.10-2	5,168	1,404
85	0,208	1,822	0,914	0,131.10-2	0,746.10-2	3,239	0,914
90	0,170	0,992	0,500	0,263.10-2	0,0149	1,613	0,499
95	0,128	0,426	0,213	0,728.10-2	0,0411	0,6	0,213
97	0,100	0,204	0,102	0,180.10-1	0,103	0,241	0,102

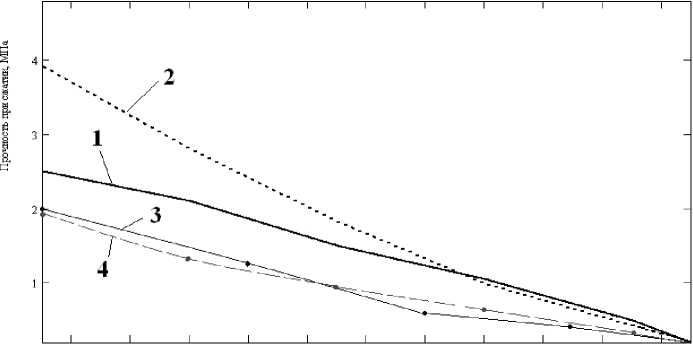
76         78         80         82         84         86         88         90         92         94         96

Пористость, %

Рис. 5. Зависимость расчетной (1, 3) и экспериментальной (2, 4) прочности при сжатии от пористости: 1, 2 – оксид алюминия Al 2 O 3 ; 3, 4 – электрофарфор

Из рис. 5 видно, что в диапазоне пористости 85-97% получено удовлетворительное соответствие расчетных и экспериментальных данных. Повышение точности результатов в исследованном интервале пористости связано с необходимостью учета следующих факторов: анизотропии ячейки, так как реальная ячейка имеет вытянутую форму с отношением диаметров ячейки 2,0-2,5; реального строения перемычки, представляющей собой разомкнутую оболочку с закрытой и канальной пористостью; фактических свойств материала основы с учетом технологических особенностей его изготовления.

Выводы:

• 1.    Установлена зависимость между величиной сжимающей нагрузки и локальными напряжениями и перемещениями в структурных элементах ячейки высокопористого ячеистого материала, представленной в виде тетракаидо-декаэдра.

• 2.    Разработана методика расчета эффективных значений предела прочности и модуля упругости материала в зависимости от величины разрушающего напряжения компактного материала и геометрических параметров структуры.

• 3.    Приведены результаты расчета величины разрушающего напряжения и модуля упругости высокопористой керамики Al 2 O 3 и

  электрофарфора в интервале пористости 7597%. Представлены результаты анализа сравнения расчетных параметров с экспериментальными данными.