Структурное состояние ксерогелей на основе жидкого стекла, модифицированных никелем, кобальтом и титаном

Материалы, находящиеся в аморфном состоянии, являются предметом многих современных теоретических и экспериментальных исследований. Особый интерес представляет высокодисперсный аморфный кремнезем, который обладает целым комплексом свойств, позволяющих широко использовать его как активный наполнитель для полимерных и смазочных материалов, сорбентов в хроматографии, а также в би- отехнологии, медицине, фармации и сельском хозяйстве [9], [14]. На базе высокодисперсных кремнеземных порошков, синтезированных на основе жидкого стекла, создаются новые машиностроительные материалы с повышенными физико-механическими характеристиками [5], [10], [11], [15], [16]. Одним из методов кардинального изменения свойств кремнезема является его химическое модифицирование [4], [6], [17], позволяющее синтезировать порошки с новыми

свойствами. Получение материалов со строго заданными свойствами всегда связано с четким пониманием особенностей их структуры. Таким образом, изучение структурных изменений в высокодисперсных кремнеземных порошках, синтезированных на основе жидкого стекла, при модифицировании их различными добавками является актуальной научно-технической задачей. Целью работы было исследование структурных изменений образцов ксерогелей, полученных из водного раствора щелочного силиката (ВРС) при модифицировании никелем, кобальтом и титаном.

МАТЕРИАЛЫ И МЕТОДЫ ИССЛЕДОВАНИЯ

Образец ксерогеля был получен из водного раствора силиката при дегидратации до постоянного веса при 200 °C. В качестве водного раствора щелочного силиката использовали стандартное натриевое жидкое стекло (ЖС, ГОСТ 13078, силикатный модуль n = 2,9 ± 0,1, плотность ρ = 1,45 г/см³). Композиции ЖС-мeталл получали совмещением модификатора, в роли которого выступали соли металлов TiC₂O₅, NiSO₄ и CoSO₄, с водным раствором ЖС, после чего смеси дегидратировали, высушивали при 325–330 К, диспергировали и просеивали. Исследования атомной структуры проводили методом рентгеноструктурного анализа. Рентгенограммы получены на дифрактометрах типа ДРОН в Сu- и Mo-K_α-излучениях, монохрома-тизированных кристаллами пиролитического графита в первичных и отраженных лучах. Рентгенографирование образцов проводилось в геометриях на отражение и на просвет в интервале углов рассеяния 2 0 от 2 до 145° с шагом по углам от 0,2 до 0,5° и временем экспозиции в каждой точке 20 с.

Полученные в эксперименте кривые распределения интенсивности рассеяния нормировались на составы: Na2Si3O7, Na2Si3O10.12Co0.78S0.78, Na2Si3O9.88Ni0.72S0.72 и Na2Si3O11Ti0.8C1.6, которые были рассчитаны из данных о композициях ЖС – соли металлов. При анализе результатов эксперимента использовался метод Уоррена – Финбака.

Из нормированных экспериментальных зависимостей интенсивности рассеяния I ( S ) от длины дифракционного вектора S = (4 n sin 0 ) / X рассчитывались функции H ( S ), являющиеся подынтегральными для расчета кривой распределения парных функций D ( r ) и равные:

H ( S ) = S ■ i ( S )exp( - a ² S ²) g ^{- 2}( S ) , (1)

где i(S) – интерференционная функция рассеяния, exp(-a2S2) - множитель затухания. Функция g–2 (S) представляет собой фактор обострения и вводится для повышения контрастности интерференционной картины при больших значениях S. Численным интегрированием функ- ции H(S) рассчитывали кривую распределения парных функций D(r):

max

D ( r ) = 2 n ² r p e £ Z j + J H ( S )sin( Sr ) dS , (2) j 0

где ρ_e – средняя электронная плотность, Z_j – атомный номер j -го элемента, входящего в состав исследуемого материала.

Экспериментальную функцию D ( r ) можно представить в виде суммы функций парного взаимодействия атомов P_ij ( r ), каждая из которых домножена на отношение координационного числа к радиусу соответствующей координационной сферы:

N

D ( r ) = £ £ — ^ -( r ) . (3) ij r ij

Парная функция P_ij ( r ) характеризует распределение электронной плотности отдельно взятой пары атомов, находящихся на расстоянии r_ij друг от друга. Значения парных функций в зависимости от расстояния r рассчитываются из известных данных о функциях атомного рассеяния атомов i , j . Детально методика введения поправок в экспериментальные кривые распределения интенсивности и обоснование расчета H ( S ) и D ( r ) по формулам (2, 3) изложены в работах [2], [19].

Поскольку кривая распределения парных функций D ( r ) линейно связана со значениями координационных чисел N_ij , то, задавая значения радиусов r_ij координационных сфер и их дисперсий σ_ij , координационные числа N_ij можно рассчитать методом наименьших квадратов (МНК). Дальнейший анализ структуры проводился в несколько этапов [8]:

• 1.    Поиск кристаллических модификаций, химический состав которых соответствует химическому составу исследуемых материалов;

• 2.    Расчет для каждой кристаллической фазы наборов радиусов координационных сфер, их дисперсий и координационных чисел;

• 3.    Использование рассчитанных для кристаллических модификаций значений радиусов координационных сфер и их дисперсий в качестве исходных данных для расчета координационных чисел МНК из D ( r )_эксп;

• 4.    Варьирование значений радиусов и их дисперсий с одновременным расчетом (на каждом шаге) координационных чисел МНК до тех пор, пока различие между D ( r )_эксп и D ( r )_выч не станет меньше или равным погрешности в значениях D ( r ) _эксп во всех точках интервала подгонки;

• 5.    Сопоставление рассчитанных из эксперимента характеристик ближнего порядка ( r_ij , σ_ij и N_ij ) с соответствующими данными, рассчитанными для кристаллических фаз. Анализ различий между ними, интерпретация полученных результатов.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Введение в исходную силикатную матрицу модифицирующих добавок меняет наблюдаемую картину рассеяния рентгеновских лучей: изменяется форма основного диффузного максимума и появляются дополнительные максимумы. Следует отметить, что ход кривых рассеяния, полученных от образцов, модифицированных никелем (Ni) и кобальтом (Co), подобен. На кривой рассеяния образцов с титаном (Ti) присутствуют очень слабые линии кристаллической фазы. На всех кривых появляется интенсивное рассеяние в области малых углов, которое не наблюдалось для исходного ксерогеля. Следовательно, при введении в силикатную матрицу ионов металлов возникают достаточно крупные области неоднородностей электронной плотности.

Рентгенографирование образцов с использованием разного типа излучений позволяет получить картины рассеяния в отличных друг от друга пределах значений длины дифракционного вектора S, что увеличивает информативность дифракционного эксперимента. На рис. 1 срав- ниваются картины рассеяния образцами ЖС с интеркалированными в него ионами кобальта и титана, полученные на излучениях CuKα и MoKα .

На рис. 1а видно, что интенсивное рассеяние в области малых углов (рис. 1б), которое наблюдается при проведении эксперимента на излучении MoK _α , выявляется как дополнительный диффузный максимум на излучении CuK _α . Аналогичный эффект наблюдается и для системы ЖС-Ni. Данный максимум, по-видимому, обусловлен когерентным рассеянием регулярно расположенными неоднородностями электронной плотности примерно одного и того же размера. Для системы ЖС-Ti на картине рассеяния, полученной на излучении CuK _α , наблюдается перегиб при значении S, примерно соответствующем положению первого максимума на рис. 1а, и рост интенсивности рассеяния с уменьшением угла. Более детальную информацию о природе и характере распределения неоднородностей электронной плотности можно получить методом малоуглового рассеяния (МУР) [7].

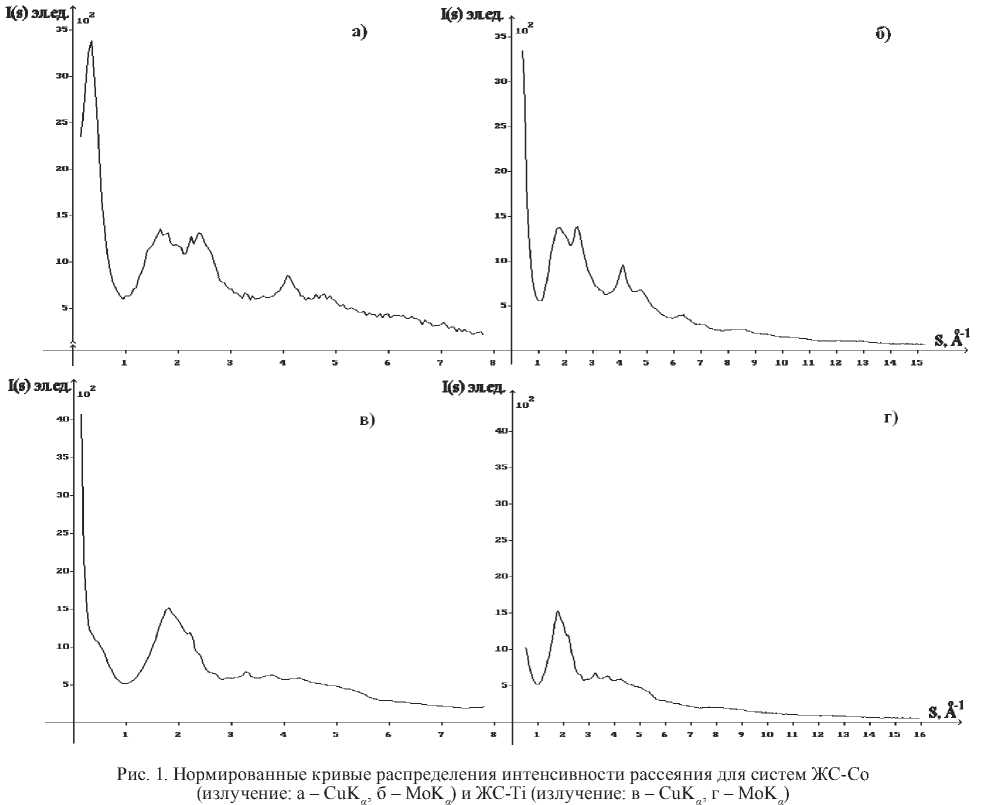
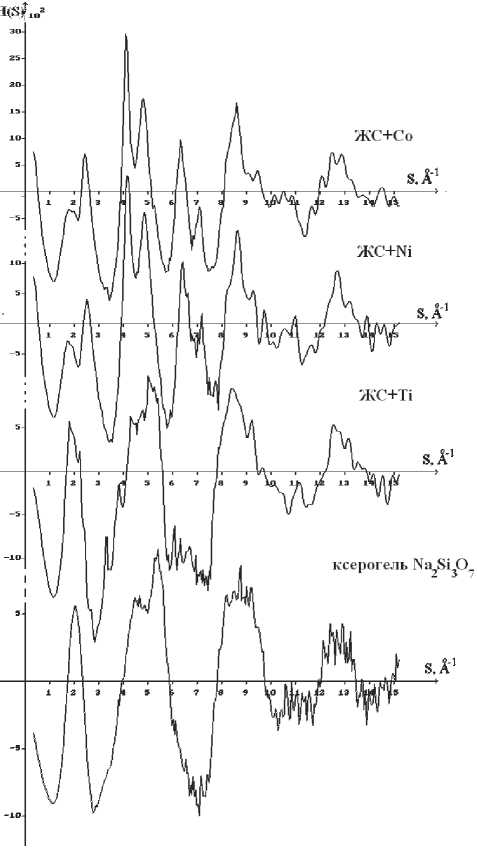
Рис. 2. S-взвешенные интерференционные функции рассе- яния для образцов с интеркалированными в силикатную матрицу ионами Co, Ni, Ti в сравнении с таковыми для образца ксерогеля, полученного дегидратацией при 200 °C

На рис. 2 и 3 представлены функции H ( S ) и D ( r ) для образцов с интеркалированными в силикатную матрицу ионами кобальта, никеля и титана в сравнении с таковыми для образца ксерогеля, полученного дегидратацией при 200 ° C.

На кривых распределения S -взвешенных интерференционных функций H ( S ) (рис. 2) более ярко выражены различия в дифракционной картине, чем на кривых распределения I ( S ). Как следует из рис. 2, интерференционные функции H ( S ), полученные для образцов с Ni и Co, близки друг к другу. Кривая распределения H ( S ) для образца с Ti ближе к таковой для исходного ксерогеля. Следовательно, характер взаимного расположения атомов в системах ЖС-Co и ЖС-Ni подобен, но отличается от упорядочения в исходном (нелегированном) ЖС. Легирование титаном изменяет кривую H ( S ) по сравнению с H ( S ) от

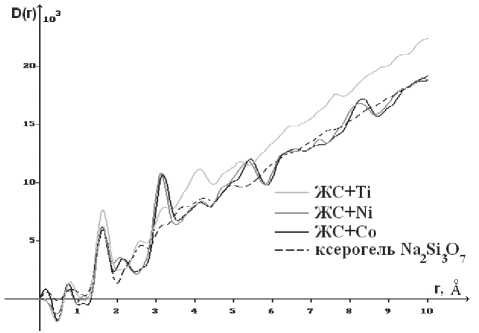
Рис. 3. Кривые распределения парных функций D(r) для образцов с интеркалированными в силикатную матрицу ионами Co, Ni, Ti в сравнении с таковыми для образца ксерогеля, полученного дегидратацией при 200 °C

ЖС не столь значительно. Присутствие на кривой H ( S ) для образца ЖС-Ti небольших узких пиков означает, что он содержит некоторое количество кристаллической фазы, идентифицировать которую из-за малого числа отражений не удалось.

Из анализа кривых распределения парных функций D ( r ), представленных на рис. 3, видно, что первый максимум для всех образцов наблюдается при r = 1,62 Å, что отвечает среднему значению кратчайших расстояний Si-O в тетраэдрах SiO₄. Ход зависимостей D ( r ) отличается друг от друга, что свидетельствует о различии ближнего порядка в расположении атомов. Осцилляции на кривых D ( r ) затухают при различных значениях r , следовательно, дальность корелляции ( R_D ) в расположении атомов различна: для образцов с Ti и исходного ксерогеля R D ~ ⁵ А, а для образцов с Ni и Co значение R_D почти вдвое выше ( R D ~ 9 А). Таким образом, при интеркалировании в силикатную матрицу ионов Ni и Co размеры области ближнего упорядочения увеличиваются.

Для всех рассматриваемых образцов из кривых распределения парных функций D ( r ) методом последовательных приближений [2] были рассчитаны радиусы r_ij и размытия σ_ij (дисперсии радиусов) координационных сфер. Координационные числа вычислялись при решении системы условных уравнений (3) методом сингулярного разложения, который оказался более устойчивым по сравнению со стандартным МНК. Результаты расчетов приведены в табл. 1–3. Погрешности в определении радиусов A r ij = ± 0,01 А и дисперсии радиусов Δ σ_ij = 0,02 Å.

Из табл. 1 видно, что в исходном состоянии ЖС характер ближнего упорядочения подобен порядку в кристаллической фазе Na2Si3O7 [13]: различия в значениях радиусов координационных сфер незначительно выходят за пределы погрешности. Число ближайших кислородных

Таблица 1

Результаты расчета характеристик ближнего порядка для исходного ксерогеля в сравнении с данными, рассчитанными для кристаллической фазы Na2Si3O7

Тип сферы Na2Si3O7 [15] ЖС Радиус сферы Дисперсия радиусов Вычисл. координ. числа rij, Å Nij, ат. rij, Å σij, Å Nij± Δ Nij, ат. Si-O [O-Si] 1,62 4,000 [1,714] 1,62 0,15 4,0 ± 0,2 [1,7 ± 0,1] Na-O [O-Na] 2,44 5,000 [1,429] 2,38 0,24 6,3 ± 0,3 [1,8 ± 0,1] O-O 2,65 5,140 2,69 0,10 6,9 ± 0,3 Si-Si 3,07 3,330 3,05 0,13 4,4 ± 0,2 Na-Na 3,39 0,500 3,36 0,14 0,5 ± 0,1 соседей, окружающих атом кремния, равно 4, то есть тетраэдры SiO4 сохраняются. Мотив связи тетраэдров SiO4 в ЖС и в кристаллической фазе Na2Si3O7 одинаков: NO-Si = 1,7 в ЖС и в кристаллической фазе Na2Si3O7, но отличается от такового в кварце: в чистом кварце NO-Si = 2, то есть тетраэдры SiO4 соединяются вершинами через общий атом кислорода. Это различие обусловлено наличием в ЖС в окрестности тетраэдров SiO4 ионов Na, стремящихся также окружить себя ионами кислорода. Однако 4-угольная пирамида NaO5 в ЖС достраивается до октаэдра NaO6, то есть в ЖС ионы Na находятся в октаэдрическом окружении (NNa-O = 6,3), и эти октаэдры NaO6 соединяются вершинами: NO-Na = 1,8. Характер упаковки этих структурных элементов в аморфном ЖС отличается от мотива их расположения в кристалле Na2Si3O7 уже в силу того, что и сами элементы различны: 4-угольная пирамида NaO в кристалле Na Si O и октаэдр NaO6в ЖС. 5 2 3 7

При внедрении в ЖС кобальта характер ближнего порядка становится подобен таковому для кристаллической фазы Na2CoSi4O10 (табл. 2). Об этом свидетельствует тот факт, что значения радиусов координационных сфер практически одинаковы. Следует отметить, что в табл. 2 и 3 для координационных сфер разного типа, имеющих одинаковые радиусы, для сравнения с экспериментом были рассчитаны средневесовые значения радиусов и суммарные координационные числа по методике, предложенной в [1].

Анализ данных, представленных в табл. 2, показывает, что кобальт, внедряясь в структуру ЖС, стремится окружить себя атомами кислорода, мешая при этом образованию кремний-кислородного каркаса из тетраэдров, подобного таковому в ЖС. Об этом свидетельствует понижение координационного числа на сфере O-Si от NO-Si = 1,7 (табл. 1) для исходного ЖС до NO-Si = 1,1 (табл. 2) для системы ЖС-Со. Кремний-кислородные тетраэдры при этом сохраняются (NSi-O = 3,8 ± 0,2).

Кислородное окружение иона Co несколько отличается от такового в кристаллической фазе Na2CoSi4O10. В последней число атомов кислорода, окружающих кобальт, равно 5 (NCo-O = 5), то есть координационный многогранник – четырехугольная пирамида. В системе ЖС-Со координационное число NCo-O = 4,5, то есть наряду с пирамидами СоО5 имеются тетраэдры СоО4.

Необходимо отметить тот факт, что координационные числа, рассчитанные из эксперимента для системы ЖС-Со вплоть до 6-й сферы, близки к данным для кристалла Na2CoSi4O10, однако на 7-й сфере имеет место резкое возрастание числа атомов. Нет совпадения и на последующих двух сферах. Причина этого – изменение взаимной ориентации координационных многогранников кремния и металлов в пространстве.

Характеристики ближнего порядка, полученные для образца с Ni (табл. 2), коррелируют с данными, приведенными для образца с кобальтом, и с данными, рассчитанными для кристалла Na2NiSi4O10, но, в отличие от системы ЖС-Со, в аморфной фазе ЖС-Ni так же, как и в кристалле, никель в основном окружен 5 атомами: NNi-O = 4,9. Тем не менее все рассмотренные выше для системы ЖС-Со особенности в поведении координационных чисел наблюдаются и в системе ЖС-Ni.

Таким образом, при внедрении в ЖС ионов Ni и Co в аморфных системах возникает ближний порядок, близкий к расположению атомов в изо-структурных кристаллических фазах Na2NiSi4O10 и Na2CoSi4O10 [3] в области ближайшего окружения, но отличающийся по взаимной ориентации координационных многогранников в пространстве.

В случае модифицирования ЖС ионами Ti в системе ЖС-Ti ближний порядок становится подобен таковому для кристаллической фазы Na2TiSi4O10 (табл. 3). Об этом свидетельствуют практически совпадающие значения радиусов координационных сфер.

Однако число кремниевых соседей у атома кислорода уменьшается до NO-Si = 1,2 вместо 1,4 для кристаллической фазы Na2TiSi4O10, то есть мотив взаимного расположения тетраэдров SiO4 различен.

Увеличение числа кислородных соседей у атома кремния до 4,2, возможно, обусловлено замещением части атомов кремния в тетраэдрах атомами титана.

Кроме того, число ближайших соседних атомов кислорода у ионов титана (NTi-O = 3,3) вдвое ниже, чем в кристаллической модификации, в которой титан находится в октаэдрической координации. Координационное число для натрия также занижено: NNa-O = 4,1 в системе ЖС-Ti вместо 5 в кристалле. Таким образом, несоответствие координационных чисел, определенных из эксперимента для системы ЖС-Ti, соответствующим данным для кристалла Na2TiSi4O10 начинается уже с ближайшего окружения. С учетом

Таблица 2

Результаты расчета характеристик ближнего порядка для системы ЖС-M в сравнении с данными, рассчитанными для кристаллической фазы Na2MSi4O10 (M = Co, Ni)

№ сферы Объединяемые сферы rij. Å Nij. ат. Тип сферы . Å . ат. rij. Å σij. Å Nij± Δ Nij, ат. Na2CoSi4O10 [14] ЖС-Co 1 Si-O [O-Si] 1,63 4,0 [1,6] Si-O [O-Si] 1,63 4,0 [1,6] 1,62 0,08 3,8 ± 0,2 [1,1 ± 0,2] 2 Co-O 2,04 5,0 Co-O 2,04 5,0 2,11 0,10 4,5 ± 0,2 3 Na-O 2,43 4,0 Na-O 2,43 4,0 2,43 0,15 3,3 ± 0,1 4 O-O 2,67 5,5 O-O 2,67 5,5 2,69 0,10 2,9 ± 0,2 5 Na-O 2,80 2,5 Na-O 2,80 2,5 2,80 0,01 1,8 ± 0,1 6 Si-Si 3,04 3,0 Si-Si 3,04 3,0 3,06 0,02 3,7 ± 0,2 7 Co-Co 3,23 1,0 Co-Co 3,25 2,49 3,25 0,23 12,4 ± 0,5 Si-Co 3,24 1,25 Na-Si 3,28 4,0 8 Na-Co 3,41 1,5 Na-Co 3,46 2,80 3,45 0,22 0,7 ± 0,3 Na-Na 3,50 0,5 O-O 3,52 5,1 9 Co-O 3,59 4,0 Co-O 3,63 12,2 3,64 0,12 15,1 ± 0,7 Na-Si 3,61 3,0 Na-O 3,64 5,0 Si-O 3,66 7,75 Na2NiSi4O10 [14] ЖС-Ni 1 Si-O [O-Si] 1,61 4,0 [1,6] Si-O [O-Si] 1,61 4,0 [1,6] 1,62 0,09 3,8 ± 0,2 [1,2 ± 0,2] 2 Ni-O 2,07 5,0 Ni-O 2,07 5,0 2,08 0,11 5,1 ± 0,3 3 Na-O 2,46 4,0 Na-O 2,46 4,0 2,38 0,10 2,5 ± 0,1 4 O-O 2,66 5,5 O-O 2,66 5,5 2,69 0,12 3,3 ± 0,2 5 Na-O 2,75 2,5 Na-O 2,75 2,5 2,75 0,01 2,2 ± 0,1 6 Si-Si 3,05 3,0 Si-Si 3,05 3,0 3,05 0,01 3,9 ± 0,2 7 Ni-Ni 3,17 1,0 Ni-Ni 3,20 2,41 3,20 0,24 11,3 ± 0,6 Si-Ni 3,19 1,25 Na-Si 3,25 4,0 8 Na-Ni 3,44 1,5 Na-Ni 3,46 2,74 3,46 0,23 0,6 ± 0,1 O-O 3,49 5,0 Na-Na 3,51 0,5 9 Ni-O 3,55 4,0 Ni-O 3,61 11,9 3,61 0,12 14,1 ± 0,5 Na-Si 3,63 3,0 Na-O 3,63 5,0 Si-O 3,64 7,75 вдвое меньшего значения дальности корреляции это означает, что беспорядок в расположении атомов в системе ЖС-Ti выше, чем в системах ЖС-Со и ЖС-Ni.

ЗАКЛЮЧЕНИЕ

Из анализа характеристик ближнего порядка, рассчитанных для ксерогелей на основе жидкого стекла, модифицированных никелем, кобальтом и титаном, следует, что при образовании систем ЖС-металл кремний-кислородные тетраэдры сохраняются, однако их взаимная ориентация в пространстве меняется. Изменяется и координационное окружение атомов металлов по сравнению с таковым в кристаллах близкого состава.

Полученные в данной работе характеристики ближнего порядка во взаимном расположении атомов могут быть использованы для формирования компьютерных моделей пространственного расположения атомов в исследованных ксерогелях как в исходном состоянии, так и при легировании атомами различных металлов.

Таблица 3

Результаты расчета характеристик ближнего порядка для системы ЖС-Ti в сравнении с данными, рассчитанными для кристаллической фазы Na2TiSi4O10

Na2TiSi4O10 [20]							ЖС-Ti
№ сферы	Объединяемые сферы	r ij . Å	Nij. ат.	Тип сферы	ij>. Å	ij>. ат.	r ij . Å	σij. Å	Nij±Δ Nij. ат.
1	Si-O [O-Si]	1,62	4,00 [1,45]	Si-O [O-Si]	1,62	4,00 [1,45]	1,62	0,01	4,2 ± 0,2 [1,2 ± 0,1]
2	Ti-O	1,97	6,00	Ti-O	1,97	6,00	1,97	0,01	3,3 ± 0,1
3	Na-O	2,46	5,00	Na-O	2,46	5,00	2,38	0,01	4,1 ± 0,2
4	O-O	2,66	5,82	O-O	2,66	5,82	2,66	0,01	5,0 ± 0,2
5	Na-O	2,72	2,00	Na-O	2,72	2,00	2,76	0,02	0,6 ± 0,1
6	O-O	2,89	0,73	O-O	2,89	0,73	2,93	0,01	0,13 ± 0,01
7	Si-Si	3,05	3,00	Si-Si	3,05	3,12	3,05	0,12	7,5 ± 0,2
	O-O	3,08	0,36
8	Na-Si	3,21	2,00	Na-Ti	3,22	3,37	3,20	0,01	0,6 ± 0,1
	Na-Ti	3,23	2,00
	O-O	3,27	0,36
9	Si-Ti	3,33	1,00	Si-Ti	3,33	1,00	3,35	0,01	1,3 ± 0,1
10	Na-O	3,46	1,00	Na-Na	3,54	8,28	3,52	0,03	14,2 ± 0,3
	Na-Na	3,51	2,00
	Si-O	3,56	6,00
11	Na-Si	3,61	4,00	Na-Si	3,61	5,21	3,61	0,05	4,0 ± 0,2
	O-O	3,64	2,91

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.