Структурный и параметрический синтез рычажно-винтового исполнительного механизма виброперемешивающего устройства

перспективность применения кривошипноползунных, кулисных и других рычажных механизмов в качестве исполнительного механизма (ИМ) ВПУ. Однако применение простых рычажных механизмов в ВПУ не позволяет обес- печить оптимальные для технологического процесса амплитуды колебаний рабочих органов. Это связано с тем, что размеры кривошипа в этих механизмах, задающие амплитуду колебаний рабочих органов, определяются, прежде всего, мощностью привода, а не требованиями технологического процесса. Для решения данной проблемы синтезируем новый ИМ ВПУ, у которого амплитуда колебаний рабочих органов будет определяться только технологическими про- цессами.

Структурный синтез ИМ ВПУ. Для решения поставленной задачи синтезируем сложный [6], состоящий из двух простых, рычажный ИМ ВПУ. Синтез ИМ ВПУ проведем с использованием структурной математической модели [6] которая имеет вид:

1 Г           )

p =—I у tn, + ^ ;

t

² i t = T - j        j

T n = 2 n _t ; t = t - j

П - ¹

\ W = 2 pit- kn ;

i = 1

k = p - n ;

n - 1

p = 2 pip i = 1

T <  k + 1.

где р – общее число кинематических пар; Т – количество вершин базового звена; t – число вершин звеньев; n – общее число подвижных звеньев; n t – число подвижных звеньев с t вершинами; р i – число кинематических пар i -той подвижности; k – число независимых замкнутых контуров; П – подвижность пространства, в котором синтезируется механизм; S – число присоединений к стойкам; i =1, 2, 3, 4, 5 – целочисленный индекс; j =0, 1, 2, … целочисленный индекс.

Синтез первого механизма. Так как желательно, чтобы ИМ ВПУ был относительно не сложным, то пусть синтезируемый механизм будет существовать в трехмерном (M=3) трехподвижном (П=3) пространстве; иметь одну степень свободы (W=1); иметь один независимый контур (k=1); иметь двухвершинное базовое (Т=2); иметь только одноподвижные вращательные кинематические пары. Структурная математическая модель (1) после подстановки в нее исходных данных примет вид p=2 (2 n 2 + S);

n = ⁿ 2 ;

< 1 = p 1 - 3;

1 = p ^- n ;

^p = ^p i^;

2 < 2.

Понятно, что в синтезируемом механизме число звеньев, кинематических пар и присоединений к стойке должно быть целым и положительным. Следовательно, решение модели (2) должно удовлетворять этим условиям. Целочисленными корнями модели (2) являются следующие значения: р =4; n =3; S =2.

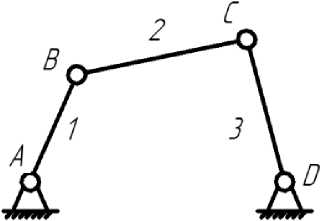
Рис. 1. Шарнирный четырехзвенник:

А, В, С, D – кинематические пары; 1, 2, 3 – подвижные звенья

Из найденного решения следует, что синтезируемый механизм должен иметь: четыре одноподвижные вращательные кинематические пары; три подвижных звена; два присоединения к стойке. По найденному решению и условиям синтеза можно создать только один механизм – шарнирный четырехзвенник (рис. 1). Этот механизм преобразует вращательное движение кривошипа 1 в возвратно-вращательное движение коромысла 3.

Синтез второго механизма. Так как желательно чтобы ИМ ВПУ был относительно не сложным, то пусть второй синтезируемый механизм будет существовать в двухмерном ( М =2) двухподвижном ( П =2) пространстве; иметь одну степень свободы ( W =1); иметь один независимый контур ( k =1); иметь двухвершинное базовое ( Т =2). Так как этот механизм должен будет преобразовывать возвратно-вращательное движение в поступательное, то при его создании будем использовать вращательные, поступательные и винтовые одноподвижные кинематические пары. Структурная математическая модель (1) после подстановки в нее исходных данных примет вид:

p = 2 (2 n 2 + S);

• n = n 2^;

• < 1 = p i - 2;

• 1    = p ^- n ;

^p = p 1^;

• 2    < 2.

  
  

Целочисленными корнями модели (3) являются следующие значения: р =3; n =2; S =2. Из найденного решения следует, что синтезируемый механизм должен иметь: три одноподвижные кинематические пары; два подвижных звена; два присоединения к стойке. Анализ решения (3) показал, что синтезу ВПУ соответствует структурная схема винтового механизма, приведенная на рис. 2. Из рис. 2 видно, что этот механизм преобразует вращательное движение звена 1 в поступательное движение штока 2.

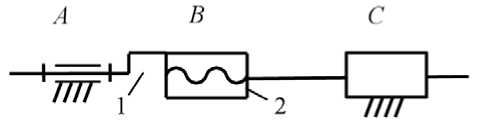
Рис. 2. Винтовой механизм.

А, В, С – кинематические пары; 1, 2 –подвижные звенья

Объединив синтезированные механизмы (рис. 1, рис. 2) получим сложный кривошипновинтовой механизм, представленный на рис. 3. В предложенном механизме вращательное движение кривошипа преобразуется в возвратно-вращательное движение коромысла, а затем винтовым механизмом трансформируется в возвратно-поступательное движение выходного звена. Амплитуда колебаний рабочего органа (выходного звена) определяется не размерами кривошипа, а углом поворота коромысла и параметрами резьбы, поэтому она всегда может быть согласованна с требуемой технологическим процессом.

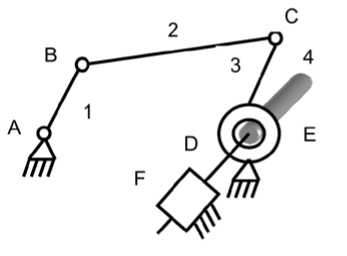
Рис. 3. Кривошипно-винтовой механизм.

A, B, C, D – вращательные кинематически пары; E, F – соответственно, винтовая и поступательная кинематически пары; 1, 2, 3, 4 – подвижные звенья

Параметры резьбы определяются диаметром винта, поэтому создание рационального ИМ ВПУ сводится к параметрическому синтезу шарнирного четырехзвенника по заданному углу колебаний коромысла, при наложенных ограничениях на коэффициент изменения средней скорости к (отношение времени прямого хода ко времени обратного хода) и угол давления в одном из крайних положений (β).

Параметрический синтез ИМ ВПУ. Для решения поставленной задачи, как и в [7] построим модифицированную расчетную схему шарнирного четырехзвенника с заданным углом колебаний α в крайних положениях коромысла.

Построение расчетной схемы (рис. 4) проводим следующим образом. Строим равнобедренный треугольник DC 2 C 1 , со сторонами DC 1 и DC 2 равными длине коромысла l 3 , и углом а. Проводим биссектрису DE угла α. Определяем угол Θ между крайними положениями шатуна

1-к

0 = 180°--.

• 1    + к            (4)

Из точки С1 или С2 под углом 90°-Θ к С1С2 проведем линию С1F или C2F, до пересечения (точка F) с линией DE. Из точки F радиусом C1F строим дугу окружности. Из точки С2, под углом 90+β к отрезку DС2, проводим линию до пересечения с дугой окружности (точка А). Соединяем точку А с точкой С1 отрезком АС1. Точки A и D определяют место расположения одноименных (см. рис. 3) кинематических пар, соединяющих кривошип и коромысло со стойкой, а отрезок AD определяет расстояние l0 между этими кинематическими парами. С1, С2 и B1, B2 – соответственно, положения кинематических пар С и В (см рисунок 3), при крайних положениях коромысла. Так как ∆C1ED и ∆C1EF имеют общий катет С1E (рис. 4), то радиус С1F дуги окружности определится

С 1 F = 13 • Sm(a /2) sin(0)

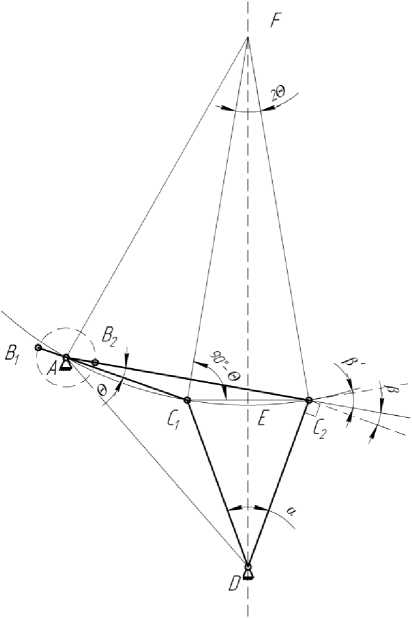
Рис. 4. Расчетная схема

Угол в' между касательной к окружности в точке С 2 и прямой АС 2 , будет

в = (а/2 + 0) - в           (6)

Длина хорды AC 2 , определится

AC2 = 2 • C 1 F • sin(в').

Угол AFC 1 , будет

AFC1 = 2 •(в— 0\

С учетом (7), AC 1 , определится

AC 1 = 2 • C1 F • sin( в'-0).

Длины кривошипа l 1 и шатуна l 2 , будут:

l _AC 2 + AC 1.

• 2    —      2;

_ AC 2 - AC 1

1         2(10)

Подставив (5), (6) , (7), (9) в (10), найдем длины кривошипа и шатуна:

f®

1, — 2 ■ sin

1           1 2

f a ® ) sin(a/2) ■ cosl - в ++ I-

(       2   2 ) sin( ® )

.1 •

3 ;

Найдем относительные длины звеньев шарнирного четырехзвенника, соответствующего следующим начальным условиям синтеза α=60°; β=20°; k=0,9. После подстановки начальных условий, в (16), (17), (18) найдем: l 13 =0,48521; l 23 =1,54021; l 03 =1,92792.

Для синтезированного шарниного четы-рехзвенника с помощью кинематической модели, приведенной в [8], построены графики угла поворота коромысла φ 3 = f (φ 1 ), и угла давления β 3 = f (φ 1 ) от угла поворота кривошипа, а так же определен средний угол давления (рис. 5).

,   „    f®^  • f  a «  ®A sin(a/2),

L — 2 ■ cosl     I ■ sinl - в + + I ■■

2         (2)    (      2   2) sin(®)

Длину l 0 найдем из треугольника AC 2 D по теореме косинусов

1 0 — 4AC 22 + DC ₂ 2 - 2 AC ₂ ■ DC ₂ ■ cos(90 - в ).

Подставив (6), (7), (8) в (14) и, обозначив

_{D n} • z a            sin(0,5 a )

B — 2 ■ sin(— + ® - в )--------

2             sin( ® ) , (14)

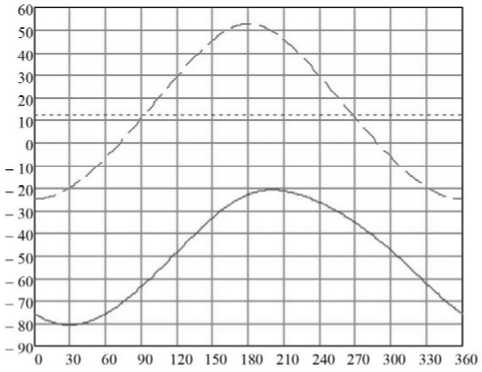
Рис. 5. Графики        - φ 3 = f (φ 1 );

β 3 = f (φ 1 ),       - средний угол давления

после ряда преобразований, найдем расстояние l 0

1 ₀ — 1 3 ■ 4B ² - 2 B ■ sin в + 1.

Для проведения целенаправленного параметрического синтеза шарнирного четырехзвен-ника представим длины его звеньев в безразмерной форме, для чего разделим (11), (12) и (15) на длину коромысла l 3 , в результате найдем искомые длины звеньев механизма:

f® ) f „ a ® ) sin( a /2)

1 — 2 ■ sin ■ cos - в ++ ;

¹³          ( 2 )     (       2   2 )    sin( ® )

(®1 • f

1 ₂₃ — 2 ■ cos l — I ■ sin l -

„ a ® ) sin( a /2) в + — + — I-------•

2   2 )

1 ₀₃ — 4 B ² - 2 B ■ sin в + 1.

sin( ® )

;

Анализ построенных графиков показывает, что: угол колебаний коромысла соответствует заданному и составляет 60°; коэффициент изменения средней скорости k , равен 0,9, что соответствует заданным условиям; угол давления β (средний – 12,151°, а максимальный – 52,717°) меньше допускаемого ([β]=60°) [9].

Выводы: синтезированный шарнирный четырехзвенник полностью соответствует начальным условиям параметрического синтеза и может быть использован в качестве ИМ ВПУ, а предложенная методика структурного и структурно-параметрического синтеза могут быть рекомендованы для использования при создании новых машин и механизмов.

Следует отметить, что разработанный параметрический синтез звеньев шарнирного че-тырехзвенника применим только при выполнении условий теоремы Грасгофа:

• 1.    Кривошип ( l 1 ) является наименьшим звеном.

• 2.    Сумма длин наименьшего и наибольшего звеньев меньше суммы длин двух других звеньев.