Структурный синтез дискретных адаптивных следящих систем на основе объединенного принципа максимума

Введение . Наиболее общий подход к синтезу следящих систем связан с решением стохастического дифференциального уравнения Стратоновича. Его конечномерная аппроксимация приводит к сеточным фильтрам с большим объемом вычислительных затрат. Поэтому практическое применение получил ставший эталоном для сравнения фильтр Калмана. Структурно подобные алгоритмы, например, расширенный фильтр Калмана, регрессионные фильтры, сигма-точечные фильтры и т. д., применяют в связи с необходимостью оценки нелинейных систем в условиях воздействия негауссовских случайных процессов [1–4]. Эффективность таких решений не очень высока, поскольку они используют аппроксимацию, обоснованность применения которой не очевидна и сводится к эмпирическим предположениям. Применение метода расширения пространства состояний и построение модели наблюдаемого процесса на основе формирующего фильтра выглядит более обоснованно. Однако не всегда реальный нелинейный процесс можно аппроксимировать линейным фильтром с достаточной степенью точности. Это связано со структурными отличиями линейных и нелинейных моделей динамики, приводящими к возникновению ошибок в следящих системах, которые можно трактовать как «структурные» и рассматривать задачу адаптации структуры модели с целью их компенсации. При реализации фильтра Калмана эти ошибки частично компенсируются за счет возникновения корреляционных связей, которые определяются решением уравнения для ковариационной матрицы ошибок фильтрации (оценки). Однако в установившемся режиме коэффициенты обратной связи подобных алгоритмов практически перестают зависеть от наблюдений и, соответственно, «структурные» ошибки полностью не компенсируются. На практике используются менее точные, но более эффективные в смысле вычислительных затрат α-β и α-β-γ алгоритмы. Это позволяет сделать вывод о возрастании ошибок, связанных с неточностью применяемой в основе фильтра оценки состояния модели [5, 6].

Применение квазидетерминистских методов в задачах синтеза следящих систем также приводит к калманов-ским алгоритмам. В частности, такой результат получают на основе методов теории регуляризации или процедуры инвариантного погружения [2,3,7]. Несоответствие положенной в основу процедуры синтеза математической модели наблюдаемому процессу в данном случае приводит к ошибкам экстраполяции и является одной из причин расхождения фильтра и срыва вычислительной процедуры [2,4,6]. Попытки предотвращения такой ситуации связаны с использованием многомодельных алгоритмов или сложных моделей, характеризующихся большим числом подлежащих определению параметров [4]. Это приводит к возрастанию размерности задачи и препятствует реализации таких решений в следящих системах в реальном масштабе времени из-за ограниченной вычислительной мощности электронных вычислительных машин [1,9]. Таким образом, для повышения эффективности следящих систем необходимо решить задачу адаптации структуры модели исследуемой системы [11,14].

Основой решения задачи структурной адаптации с успехом может служить методология объединенного принципа максимума [10–12]. Этот подход приводит к модели динамической системы, которая удовлетворяет принципу Гамильтона-Остроградского [13]. Структура модели определяется из условия максимума функции обобщенной мощности с точностью до нелинейной синтезирующей функции, определяющей скорость диссипации и, соответственно, степень структурной адаптации. Практическая реализация полученных с применением такого подхода результатов в цифровых следящих системах ставит задачу выбора схемы конечномерной аппроксимации полученной модели [9], что связано с определением вида приближения синтезирующей функции и использованием общего решения однородного дифференциального уравнения.

Целью данной работы являлась разработка метода синтеза следящих систем в дискретном времени с адаптацией структуры модели на основе методологии объединенного принципа максимума.

Постановка задачи. Пусть динамика системы в дискретном времени задана с точностью до структур переходной матрицы Ф ( k ) e R r ^х r и вектора интенсивности возмущений G ( k ) e R r линейным разностным векторным уравнением [2,5,8]

x ( к + 1 ) = Ф ( k ) x ( k ) + G ( k ) п ( к ) ,                                          (1)

где x ( k ) e R r —вектор состояния, п ( k ) — возбуждающая функция, k —момент времени.

Уравнение наблюдений имеет вид

• У ( k ) = Hx ( k ) + $ ( k ) ,                                                (2)

где H e R^1x r — матрица проекции пространства состояний на пространство наблюдений, $ ( k ) — белый гауссовский шум.

В пространстве наблюдений выбран целевой функционал

N

J = - X R - 1 [ У ( k ) - Hx ( k ) ] ,                                            (3)

• 2 k = 0

где      R ^{- 1} — параметр, который характеризует интенсивность помех в канале наблюдений, знак ^Л означает оценку.

Требуется из условия минимума целевого функционала (3) найти оценки вектора состояния x ( k ) е R^r для момента времени k , если он увеличивается [8, 11].

Синтез следящей системы на основе объединенного принципа максимума. Для решения поставленной экстремальной задачи (1)-(3) необходимо определить структуру матрицы переходов состояний Ф (k)е Rrхr и вектора ин тенсивности возмущений G (k) е Rr исходя из требований к синтезируемой следящей системе.

Математическое описание динамики системы основано на физических закономерностях и допущениях и поэтому является, как правило, приближенным, что приводит к неадекватности модели, которая трактуется как структурная неопределенность Ф ( к ) е R ^{r х r} . Например, так происходит когда в основу модели заложены лишь кинематические связи между параметрами движения [5,7].

Один из способов разрешения проблемы структурной неопределенности заключается в построении моделей с использованием утверждений, которые обеспечивают исчерпывающее описание динамики систем. За основу могут быть выбраны вариационные принципы [13]. В работе [11] с использованием принципа Гамильтона-Остроградского получена модель состояния в форме дифференциального уравнения второго порядка

■ ■ x = Q = Е

^^^^^^»

Л x

Л x

л

x

⁺ £ [ у ( t ) ^- H ( x, t ) ] ,

x (10 ) = Л x (10 ) = x 0, где е — параметр адаптации, определяющий долю регулярной составляющей приращения вектора состояния, z=IT λRξ

— параметр, определяющий вклад случайного процесса в наблюдаемое изменение состояния, Q е Gq — обобщенная сила, GQ — замкнутое ограниченное множество.

Модель (4) получена на основе условия [10]

Ф = m a x [ XQ ( x,x ) - R - [ у ( t ) - H ( x, t ) ]] x, X = const ,

где X — неопределенный множитель Лагранжа, откуда с точностью до синтезирующей функции ц ( x,x ) [12]

Q = X ¹ [ ц ( x,x ) x + R ^1 [ у ( t ) - H ( x , t ) ]] .

Для получения конечномерной аппроксимации (4) в форме векторного разностного уравнения (1) запишем его как векторное дифференциальное уравнение первого порядка. Процедура расширения пространства состояний приводит к следующему результату

x = f (x) + G П (t), x( t0) = x 0, где x =

x

[ x 2 ]

, xi = ;x, x2 = ;x, f (x ) =

- Е

. x ²

|x 11 x ₂ = A ( x ) x — вектор-функция системы для которой, А =

в

G =

Z ,

x ₂

n(t) — центрированный относительно Hx случайный процесс с интенсивностью Rn ,. в = -б x1

Рассматривается широко распространенный случай [5], когда выполняется с достаточной степенью точности условие: в = const . Тогда в дискретном времени для решения уравнения (7) справедливо [5]

t + ^А T

x ( t + А T ) = e A ^{А T}x ( t ) + J е^{л (}      ) G n ( t ) d r ,

t откуда

Ф( к) = еАА T,   G( к ^П (к) = (k +J)eA(( к+1)А T-T)G n(T)dT, кА T

где А T — фиксированный интервал дискретизации.

Вычисление матричной экспоненты приводит к матрице перехода состояний, которая определяется двумя параметрами

Ф( А T , в ) = e^{A A} T

1 e ^pA T - 1

в

0    e ^{вA T}

а вектор интенсивности возмущений сверткой

( k + 1) A T

G(k)n(k ) =  J kAT

e ^в- 1

в e ^в

z

П ⁽ T )d T =

( k + 1) A T

J kAT

ⁿ 1 ^{( t )}

n 2 ⁽ t )

n (#.

. . . eв -1

где       n i ^{( t )} = ^z~в , ⁿ 2 ( ^T ) = Z e ^в •

Решение полностью формализованной экстремальной задачи (1)–(3) с использованием дискретного варианта метода инвариантного погружения приводит к алгоритму калмановского типа [2–4, 8]

x ( k +1| k ) = Ф ( А T , в ) x ( k\k )

x ( k|k ) = x ( k|k - 1 ) + K ( k|k - 1 ) [ y ( k ) - Hx ( k|k - 1 ) ]

K ( k|k - 1 ) = P ( k|k - 1 ) н ^T [ HP ( k|k - 1 ) н ^T + R 2 ] ^{- 1} ,                                              (12)

P ( k|k - 1 ) = Ф ( А T , в ) p ( k -1| k - 1 ) ф ^T ( A T , в ) + V ( k ),

P(k|k) = P(k|k -1)- P(k|k - 1)н T [HP(k|k - 1)н T + Rf ]"' HP(k|k -1), где x(k +1 |k) — оценка x(k +1) по всем предыдущим измерениям, включая последнее k -е значение (предсказание на шаг), x(k|k) — оценка x(k) по всем предыдущим измерениям (фильтрация), K(k|k-1) — коэффициент обратной связи, P(k|k), P(k|k -1) — соответственно ковариационные матрицы оценки и предсказания на шаг,

V =

Z ² R n f е^{2 вА T} - 1 2-2e ^{вА T}   A T )

I ++I в ( 2в2         в2        в J

С2 R Гр20А T 1 1 вА ГА n e -1 1-e

1+1

в ( 2 в в J

2 2R Гр2вА T , ,   вА TA z ^‘-n е -1 1-е

1+1

в (   2в         в J z2Rn fe^f^T-!)

в I ² J

— ковариационная матрица вектора возмущений.

Исследование эффективности предлагаемого решения. Рассмотрим варианты построения следящих систем с использованием предлагаемой модели и традиционно используемых вариантов кинематических моделей для x е R ² и x е R ³ [7]

x 3 ( k - 1 ) A T ²

x1 (k) = x1 (k -1) + x2 (k- 1)AT +---—2"^-----+ ••••, i                               e e где x2 = x, x3 = x — соответственно скорость и ускорение.

При x1

L x 2 J

, H = 1 0|,

из (14) имеем [5]

Ф =

A T

1, G =

A T 2

2 A T

откуда для вектора интенсивности возмущений

( k + 1) A T

G (k) n (k )= J kA T

3 A T²

2 A T

П ( t )d r .

Его использование позволяет получить ковариационную матрицу возмущений

9 R_n A T ⁵ R A T ⁴

20       2

R A T ⁴   R A T ³

Пусть

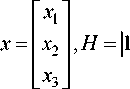
где ускорение описывается моделью формирующего фильтра в непрерывном времени [5]

i                               e

x3 = -ax3 + w,

a — постоянная времени ускорения, w — возбуждающая функция. Тогда при выборе возбуждающей функции в виде белого шума уравнения движения записываются в форме векторного дифференциального уравнения первого порядка, откуда [5]

	1 A T 1т- [ - 1 + aA T + exp [ - aA T ]]
	a 2
Ф =	0 1         — [ 1 - exp [ -aA T ]]
	a
	0 0          exp [ -aA T ]

При фиксированном а и достаточно высокой частоте поступления измерительной информации, когда aA T мало, (21) вырождается в матрицу Ньютона

1 A T

Ф = 0 1

A T ²

AT

которая может быть получена из (14). Соответственно вектор интенсивности возмущений определяется выражением [5] G ( k ) w ( k ) =

1 ( k + 1 ) A T - т - 2- [ - 1 + a (( k + 1 ) A T - t )] + exp [ - a (( k + 1 ) A T - t )] ( k + 1) A T                          a             1 J 0       1                   -[ 1 - exP [ -a(( k + 1 )A T -t) ]] k A T 0       0                   a exp [ -a (( k + 1 ) A T -t )]

" 0 " 0 w ( T )d T .               (23) _ 1 _

Из (23) получены элементы ковариационной матрицы возбуждающей функции [5]

V 11 = ^ R L [1 - e - ^{2 aA T} + 2 aA T + 2 a ² A T ² - 4 aA Te ^{-a T} ] 2 a ⁵

V = ^ R L [ e - ^{2 aA T} + 1 - e ^{-aA T} + 2 aA Te ^{-a T} + 2 aA T + a ² A T ² ] ¹²     2 a ⁴

V₁₃ = ^ R 1 [i - e - ^{2 aA T} ₊ 2 a Te ^{-aA T} ] 2 a ³

V₂₂ = ^ R ¹ [ 4 e - ^aA T - 3 - e ^{- 2 aA T} + 2 aA T ] 2 a 3

^V23 =

^{2 a R} П [ - 2 aA T 2 a^{2 1}

+ 1

-

-aA T e

2 a R

V =--- ⁿ

³³ 2 a

-

- 2 aA T e

V 21 = V 31 = V 33 = 0.

Оценка эффективности предлагаемого решения проведена на основе сравнения результатов функционирования трех моделей (13), (18) и (24) [5,7].

Рассмотрен переходной режим функционирования в условиях шумов наблюдения, когда входное возмущение задано ступенчатой функцией. На рис. 1 представлена одна из реализаций переходного процесса. Здесь цифрами обозначено: 1 — переходной процесс новой следящей системы (12); 2 — переходной процесс фильтра Калмана с моделью для равномерного движения; 3 — переходной процесс фильтра Калмана с моделью ускорения Зингера (21); 4 — возмущение. Итоги 100 вычислительных экспериментов подтверждают, что переходной процесс (12) выгодно отличается меньшей колебательностью и временем сходимости от фильтров с (18) и (22).

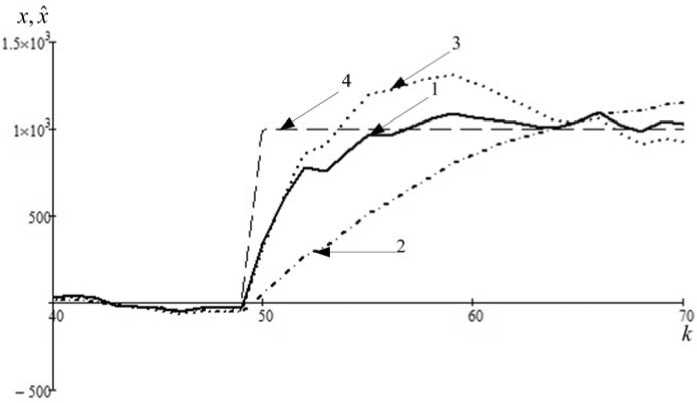
Рис. 1. Переходной процесс

Fig.1. Transient process

Анализ результатов математического моделирования позволяет сделать вывод о том, что преимущество нового решения (12) в переходном режиме достигается за счет большего коэффициента обратной связи. Это демонстрируется на рис. 2. Здесь сохранены ранее принятые обозначения.

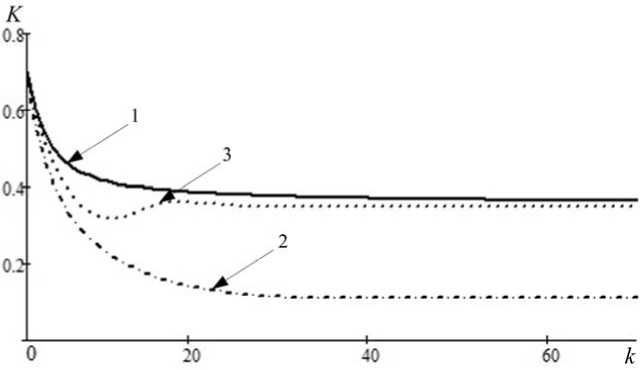
Рис. 2. Коэффициент обратной связи

Fig.2. Feedback parameter

Выводы. Разработан новый метод синтеза дискретных следящих систем на основе объединенного принципа максимума. Он обеспечивает структурную адаптацию к наблюдаемому изменению состояния за счет новой линейной динамической модели в дискретном времени. Это проявляется в высокой скорости сходимости получаемых на его основе оценок к действительным значениям по сравнению с оценками фильтров Калмана с кинематическими моделями изменения состояния [5].