Структурный синтез модульных векторных моделей, как часть общей композиции механизмов

Синтез механизмов включает в себя следующие основные задачи:

• -    динамический синтез – выбор массовых характеристик звеньев механизма с известной кинематической схемой, определяющих динамические нагрузки на звенья и механизм в целом и закон движения входного звена;

• -    кинематический синтез - выбор геометрических параметров звеньев механизма с известной структурной схемой, определяющих передаточные функции между его звеньями;

• -    структурный синтез - выбор принципиальной схемы механизма в виде последовательности звеньев, связанных кинематическими парами, определяющего возможность требуемого преобразования движения входного звена.

Динамический синтез механизма на основе оценки вариантов его кинематических схем также называют кинематическим синтезом по динамическим условиям.

Кинематический синтез механизма на основе оценки вариантов его структурной схемы можно считать структурным синтезом по заданным передаточным функциям .

В реальном проектировании чаще всего решают задачи динамического синтеза механизмов определенных кинематических схем и кинематического синтеза механизмов определенных структурных схем. Существенно реже проектировщики решают задачу кинематического синтеза по динамическим условиям оптимизации, ещё реже задачу структурного синтеза по заданным передаточным функциям.

Тем не менее, наиболее интересным, в исследовательском плане, можно считать именно структурный синтез механизмов с требуемыми

функциональными свойствами при наборе определенных ограничений. Например, заданы законы движения входного и выходного звеньев, известны различного рода ограничения на проектируемый механизм, например, габаритные, по мощности привода и неравномерности движения его звеньев, по массе, по технологичности и материалам отдельных звеньев, по габаритам кинематических пар и т.д. Требуется создать механизм, удовлетворяющий этим требованиям.

Поиск технического решения этой задачи формально можно назвать структурным синтезом по заданным параметрам оптимизации, в том числе динамическим, кинематическим, геометрическим и структурным. Однако, более правильным термином, определяющим суть процесса решения подобной задачи, следует признать термин “композиция” (придумывание, создание).

Композиция механизма представляет собой процесс поиска принципиальной, структурной и кинематической его схемы, с требуемыми функциональными свойствами при учете различных ограничений как к механизму в целом, например габаритным и массовым, так и по кинематике и динамике его звеньев. Кинематический и динамический синтез при заданной структурной схеме, а также структурный синтез можно рассматривать как частные случаи композиции механизмов.

Традиционные методы композиции механизмов основаны на следующей последовательности действий:

• 1.    выбор подходящих (или подобных) структурных схем (на основе опыта, интуиции и справочной литературы);

• 2.    перебор вариантов кинематических схем для структурных схем п.1, оценка их кинематического совершенства;

• 3.    динамический синтез вариантов кинематических схем п.2, оценка их динамического со-

• Рис. 1. Структурная схема механизма и отображающий её векторный контур

вершенства, в случае необходимости - расширение многообразия структурных схем п. 1.

Используя векторные модели (рис. 1), можно кардинально изменить метод композиции механизмов [1].

Основаниями этого утверждения являются следующие факторы [2]:

• -    абстрактные векторные модули, имеющие стандартное математическое и программное обеспечение задач о функциях и их производных, а также системы взаимосвязанных модулей обеспечивают возможность реализации достаточно широкого многообразия функциональных зависимостей как для одно-, так и для многоаргументных моделей контурных систем;

• -    любой механизм может быть отображен одним или системой взаимосвязанных векторных модулей;

• -    любой модульной модели может быть поставлено в соответствия множество вариантов конструктивно-кинематических схем механизмов.

Основываясь на данных факторах, методика композиции механизмов может состоять из следующих этапов:

• 1. Формулировка основнойфункциональной задачи.

• 2.    Переход к математической формулировке.

• 3.    Создание структурно-модульных моделей.

• 4.    Перебор и анализ возможных вариантов параметрически-модульных моделей, оценка их отклонений от требуемой передаточной функции, в случае необходимости – расширение многообразия п. 3.

• 5.    Выбор вариантов конструктивно-кинематических схем. оценка их совершенства на основе кинематических и геометрических ограничений, в случае необходимости – расширение многообразия п.4.

• 6.    Анализ вариантов динамических моделей, оценка их динамического совершенства, в случае необходимости – расширение многообразия п.4.

Принципиальное отличие предлагаемой методики композиции механизмов заключается в том, что выбираемая структурная схема механизма создается на основе предварительно синтезируемой модульной векторной модели, которая, в конечном итоге, определяет параметры кинематической схемы и динамические качества создаваемого механизма.

Реальное проектирование механизма требует достижение основной функциональной задачи с учетом кинематических, динамических и конструктивных факторов. При переходе от описательной постановки задачи к её математической формулировке выбирается целевая функция и одно или несколько дополнительных ограничений, часто существенно влияющих на выбор математической модели создаваемого механизма.

Теоретически любая математическая модель на ограниченном отрезке изменения аргументов может быть отображена не одним, а множеством систем взаимосвязанных векторных замкнутых контуров. В реальном проектировании анализируется ограниченное множество контурных моделей с минимально возможным числом векторов, образующих минимально возможное число контуров. Решение задачи синтеза модульных векторных моделей, в общем случае, сводится к выбору векторных контурных систем, реализующих в допустимых пределах целевую функцию (её минимального или максимального значения) и выполнению ряда ограничений.

Синтез векторной модели [3, 4] можно рассматривать, как переход от описательной модели создаваемого механизма к математической. Синтез векторной модели легко поддается определенной алгоритмизации в силу математической природы самой векторной модели. Анализ существующих схем, их векторных отображений приводит к выявлению некоторых закономерностей синтеза векторных моделей.

Так, например, рассмотрение требуемой траектории выходного или ведомого звена приводит к понятию его “идеальной” векторной модели, то есть произвольными модульными векторными моделями можно описать траекторию характерной точки или набор траекторий. Такие модели без учета ограничений с точки зрения описания траекторий являются идеальными. Аналогичные “идеальные” траектории могут быть созданы и для входного(ведущего) звена.

Связи между ведущими и ведомыми звеньями можно отобразить передаточными векторами, а затем - синтезировать различные варианты практической реализации этих связей с учётом различных ограничений. Выделим ключевые положения предлагаемой методики (алгоритма) синтеза векторных модульных моделей механизмов:

• 1.    целевую функцию можно отобразить векторной моделью, такую модель назовем “идеальной” векторной моделью выходного звена;

• 2.    возможный закон движения входного звена можно отобразить векторной моделью, такую

• 3.    зависимость между “идеальными” векторными моделями входного и выходного звеньев можно отобразить векторной моделью, такую модель назовем “передаточной” векторной моделью между “идеальными” векторными моделями входного и выходного звеньев;

• 4.    соединенные воедино “идеальные” векторные модели входного и выходного звеньев, и “передаточная” векторная модель определяют “общую” векторную модель;

• 5.    перебор возможных вариантов “общей” векторной модели можно проводить на основе утверждения, что синтезируемые контуры векторной модели являются элементарными векторными модулями, а так как число подобных модулей ограниченно (для плоскости четыре, а для пространства двадцать)[1], можно утверждать, что они позволяют описать все возможные функциональные зависимости;

• 6.    изменение структуры “общей” векторной модели путем модификации связей и типов модулей будем производить на основе приемов пре-образования[3];

• 7.    окончательная проработка параметров векторной модели, анализ и решение о последующих итерациях синтеза векторных моделей можно решать на основе параметрического синтеза, аналогичному параметрическому синтезу механизма.

модель назовем “идеальной” векторной моделью входного звена;

Выделим основные этапы синтеза векторных модульных моделей:

• 1.    Создание “идеальных” векторных моделей.

• 2.    Создание “передаточной” векторной модели.

• 3.    Создание “общей” векторной модели.

• 4.    Преобразование “общей” векторной модели:

• a)    анализ “передаточного вектора”;

• b)    модификация структуры векторной модели.

• 5.    Проведение параметрического синтеза векторной модели.

• 6.    Сравнительный анализ вариантов векторных моделей.

“Идеальная” векторная модель – это векторная модель, описывающая требуемые характеристики (или целевую функцию) наилучшим образом, без учета имеющихся ограничений или возможностей, т.е. “идеальная” векторная модель является векторным образом математической формулировки основной функциональной задачи. Так, например, на зададим целевую функцию разрабатываемого механизма – отклонение предкрылка на угол Δϕ и наложенные ограничения – траектория движения предкрылка по радиусу R, и необходимость размещения механизма в убранном положении в габаритах LxH. (рис. 2)

“Идеальная” векторная модель чаще всего является лишь основой для выбора вариантов структуры векторной модели проектируемого

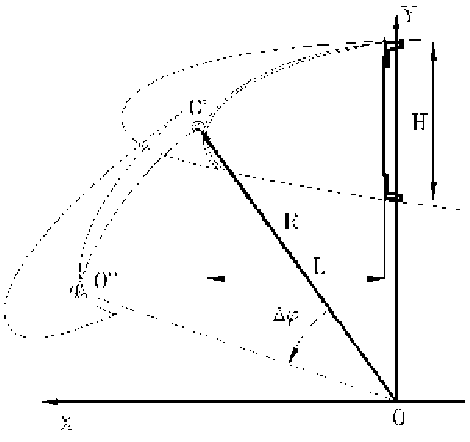
Рис. 2. Задание целевой функции и ограничений на механизм уборки-выпуска предкрылка механизма. Необходимость перехода к более сложной по структуре векторной модели определяется дополнительными ограничениями. ”Идеальность” векторной модели не означает, что она состоит из одного контура, но минимизация её состава желательна с позиций простоты конструкции будущего механизма, то есть необходимо задавать ее с учетом ограничений по числу векторов, наличию дополнительных связей и т.п. “Идеальная” векторная модель может и отдаленно не напоминать реальный механизм и, как правило, в чистом виде не пригодна для создания механизма, но она позволяет выявить закономерности для перехода к моделям, учитывающим дополнительные ограничения синтеза, например, геометрические.

Как уже было сказано выше, можно создать две “идеальные” векторные модели:

“Идеальную” векторную модель “выходного звена” - т. е. описание в векторной форме требуемого закона движения выходного звена “ (рис. 3) и “идеальную” векторную модель входного звена” - т. е. описание в векторной форме требуемого закона движения входного звена (рис. 4).

“Передаточная” векторная модель или связь между “идеальными” моделями входного и выходного звеньев в виде вектора, контура или множества контуров создается для анализа зависимости между “входным” и “выходным” звеном. Таким образом, для перехода к вариантам векторной модели создаются “идеальная” векторная модель основной функциональной задачи, “идеальная” векторная модель входного звена и “передаточная” векторная модель между двумя “идеальными” векторными моделями.

Используя понятия “идеальная” и “передаточная” векторные модели, как базовые можно

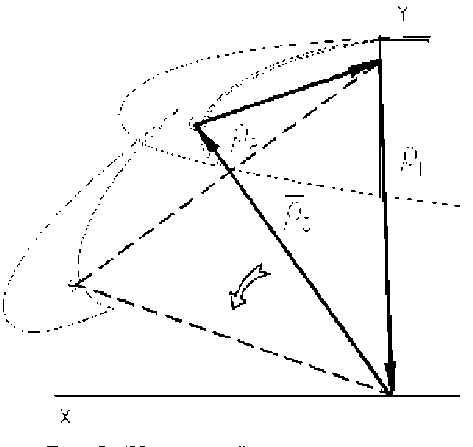
Рис. 3. “Идеальная” векторная модель “выходного звена”

Рис. 4.

“Идеальная” векторная модель “входного звена”

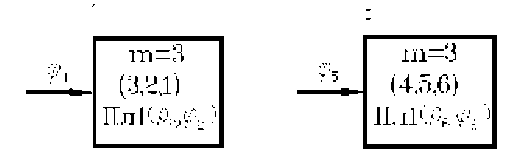
Рис. 5. Параметрическая формула “идеальной” векторной модели “выходного звена”

Рис. 6. Параметрическая формула “идеальной” векторной модели “входного звена”

систематизировать и алгоритмизировать дальнейший процесс синтеза “общей” модульной векторной модели.

Синтезированная на такой базе “общая” модульная векторная модель, должна включать в свой состав преобразованные, исходя из анализа “передаточной” векторной модели, “идеальные” векторные модели “входного” и “выходного” звеньев векторной модели, а также “передаточную” модель. (рис. 7)

Анализ “передаточной” векторной модели или анализ связей между ”идеальными” моделями входного и выходного звеньев позволяет выявить возможные варианты взаимосвязей “идеальных” моделей. На основе анализа подбирается наиболее подходящий вариант модели. Анализ заключается в сравнении поведения характеристик “передаточной” векторной модели с характеристиками элементарных векторных модулей и выбор модулей или комбинации модулей, наиболее подходящих для отображения требуемых зависимостей.

Если простой подбор модулей не дает требуемой передаточной функции и необходимо расширить поле поиска требуемой структуры, то есть, при достаточно простой векторной модели потребовалось обойти некоторое ограничение, то тогда применяются приемы, позволяющие целенаправленно изменять структуру векторной модели, ее геометрические, кинематические, и динамические параметры в зависимости от возник-

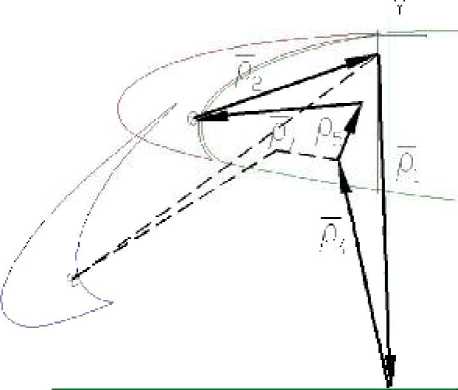
Рис. 7. “Общая” векторная модель с передаточным вектором 7

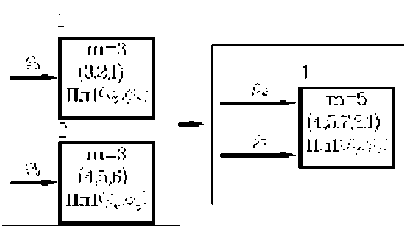
Рис. 8. Преобразование параметрических формул векторных моделей входного и выходного звена к параметрической формуле “Общей” векторной модели

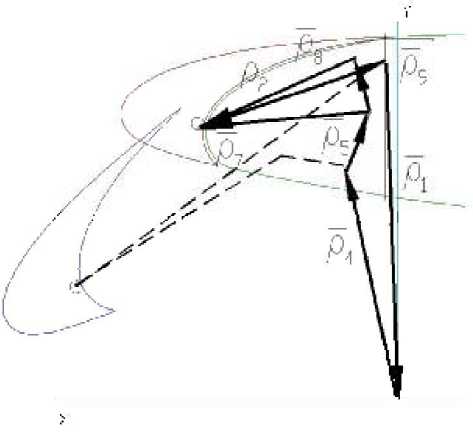
Рис. 9. Преобразованная приемами векторная модель шей ситуации. Но не только синтез “общей” модели, но и синтез “идеальных” и “передаточной” моделей может проводиться с использованием различных приемов преобразования.

Такой подход позволяет качественно оценивать структуру векторной модели и преобразовывать её с учетом всевозможных ограничений и условий. Например, в рассматриваемой модели увеличение хода передаточного вектора 7 можно добиться, используя приемы “локального дублирования” и “связывания независимых аргументов” ϕ ₉ = ϕ ₅ + Δ _5-9 (рис. 9).

В результате была получена структурная схема механизма (рис.10).

Подобных результатов нельзя добиться при параметрическом синтезе, то есть преднамерен-

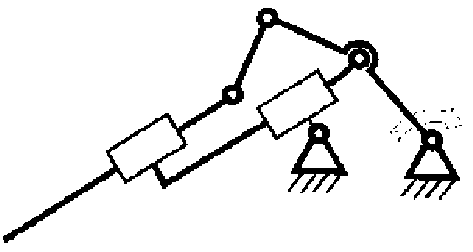
Рис. 10. Полученная структурная схема механизма но, осмысленно изменять структуру модели в нужном направлении.

В процессе структурного синтеза можно получить несколько вариантов векторных моделей, поэтому необходимо проводить сравнительный анализ их кинематического совершенства, путем оценки отклонений от требуемой передаточной функции и с учетом различных кинематических, динамических и конструктивных факторов.