Структурный синтез терминальных управлений с использованием энергии ускорений

Введение . Проблема структурного синтеза заключается в нахождении закона управления [1]. В настоящее время все больше внимания уделяется вопросам управления системой с заданным терминальным состоянием. Это обусловлено необходимостью решения таких актуальных задач, как прицельное торможение, разгон транспортных средств, наведение систем вооружения, летательных аппаратов, стыковка космических аппаратов, управление манипуляторами, демпфирование колебаний и т.д. [2, 3].

Существенный вклад в решение проблемы синтеза внесли работы Летова А.М. и Калмана Р.Э., что связано с формализмом Беллмана Р.Э. и Ляпунова А.М. [4, 5]. Одна из основных проблем в этом случае, как правило, заключается в выборе структуры и весовых коэффициентов оптимизирующих функционалов. Широкое применение также

*

∗∗

Работа выполнена по грантам РФФИ № 15-08-03798 А и № 15-38-20835 мол_а_вед.

^{∗∗∗ ‡} The research is done on RFFI grants nos. 15-08-03798 А and 15-38-20835 mol_а_ved.

находят метод приближенно – оптимального синтеза Кротова В.Ф. и функционала обобщенной работы Красовского А.А., но они не всегда обеспечивают требуемые показатели эффективности [5,6].

Одно из перспективных направлений развития теории управления состоит в использовании физических законов при построении процедур синтеза [6]. Конструктивные результаты из [7 - 15] получены с применением принципа Гамильтона – Остроградского, из которого следуют уравнения Лагранжа второго рода. Это позволяет учесть динамику действительного движения системы при построении расширенного функционала за счет включения в него интеграла действия.

В настоящей работе в отличие от [7 - 15] для решения задачи, которая заключается в разработке метода структурного синтеза терминальных управлений, предлагается использовать энергию ускорений для конструирования расширенного функционала. Применение к нему игольчатого варьирования Л.С. Понтрягина позволяет привести оптимизационную задачу к краевой, что не предполагает использования функции Беллмана [5, 16]. Достоверность полученных результатов подтверждается на основе математического моделирования при сравнении с терминальным управлением [2].

Постановка задачи. Согласно принципу Гаусса в каждый момент времени t динамическая система движется таким образом, что принуждению [17]

• n 1     I

Z = Z mAq s - - I ,s = 1 ,n ,(1)

• s=12    (

соответствующие истинному пути ускорения q_s доставляют минимум:

5Z = 0,(2)

где m s — масса материальной точки; q s — координата материальной точки относительно неподвижной декартовой системы координат; Q s — равнодействующая сил, приложенных к материальной точке; n — число степеней свободы динамической системы.

Двумя точками обозначена производная по времени. Из условия минимума функции (1) следуют уравнения в форме Аппеля [17, 18]:

5 G dqs

= Q s , s = 1 ,n ,

где G — функция Гиббса.

Пусть динамика исследуемой системы удовлетворяет (1) и, следовательно, описывается уравнениями (3).

Требуется найти допустимые силы Q _s е G q , переводящие систему (3) из заданного начального состояния

(q (t о ),q(t о )) в заданное конечное (q (t1),q(t1)) , соответствующую им траекторию (q,q )e R R , которые обеспечат минимум целевого функционала t1

J = J F(q)dt ^ min , t ₀

Где F(q) знакопостоянная и непрерывная вместе с частными производными во всей области определения функция, а t0 ,t1 — соответственно время начала и окончания управляемого процесса.

Необходимое и достаточное условие минимума целевого функционала. Поиск необходимого и достаточного условия минимума целевого функционала (4) проводится методом неопределенных множителей Лагранжа. Это требует рассмотрения расширенного функционала, который учитывает особенности динамики системы в форме выражения (1):

t ₁

J 1 = J + J X Zdt ^ min ,                                          (5)

t ₀

где X — неопределенный множитель Лагранжа.

Пусть произвольная обобщенная сила определяется выражением

Q s = Q s +5 Q s ,                                                        (6)

где Q _s — доставляющая минимум целевому функционалу обобщенная сила, а 5 Q_s = 0 при t е [ тт + A t ], те ( t ₀, t 1 ) — заданная точка непрерывности функции (Q_s At е [ т ,t 1 ] — заданный малый конечный интервал времени; A t >  0.

Тогда необходимое условие минимума целевого функционала определяется неравенством

A J ₁ = [ X Z + F ] A t t 1

t ₁

t ₁

(

л

nt ir                                          n t 1

+ z J[X5Z + 5'F]dt =[XZ + F]At(1 + E J X     5qis + Vs5qs dt > 0, s=110                                    0 s=110L (aqs     J          _

Информатика, вычислительная техника и управление

5F где Vs =--фиктивная обобщенная сила.

⁵ -7 s

Соотношения на концах траектории являются условиями трансверсальности:

[JZ + F ] = 0, если интервал [11 -t0 ] фиксирован, или

At = 0,(9)

если интервал [ 1 1 - t ₀ ] не фиксирован .

При 1 е [ 1 ₀, т ] Q = Q , поэтому AJ 1 = 0 . При 1 е [ т , т + A 1 ] AJ 1 * 0 и

2 n

5I2msУs -QS"l n 5Z1 е[т,т+А 1 ] = ~----Tv---—5q, = I(msq, - Qs )5q, .(10)

• 5    qss

При 1 е [ т + A 1 , 1 1 ] A J 1 * 0, но произвольная сила Q_s и доставляющая минимум (4) — Q _s совпадают, значит

• о    n 1

• 5    Itms qs — l s=12         m,          4\

5z, ^^a 1 ] =--------e          5qs = Ims-s -Qs)5qs.(11)

• 5 qss

Приращение подынтегральной функции целевого функционала F вычисляется следующим образом:

nn

5'F^t+a t ] = I    5qs = I Vs5qs .(12)

• 1    J s=15q ss

Тогда условие (7) записывается так:

• AJ1 = I T+^s5qs + X(m,q, - Qs >q, ]d1 + I J[x(msqs - Qs>q, + Vs5q, d > 0.(13)

s = 1 t                                           s = 1 t+A 1

Выберем теперь другие силы Q _{E s} е G q , полученные по правилу (6). Приращение функционала будет иметь аналогичный (13) вид:

• AJ1Е = I JVs5qes+X(ms^s- Q^s )5qEs ]d1 + 1I J [^(msqEs-

s = 1 t                                                s = 1 t+A 1

В силу произвольности синхронных вариаций примем условие их стыковки [9]

5 - s ( 1 ) = Sq g s ( 1 ), при ¹ = ^т . (15)

Для траекторий q_s и q ^ s , полученных для Q_s, Q _{E s} , имеем:

5 2 J = A J 1 E -A J 1 = II ^T+> e s - V s ) 5 q s +X ( m_s [ (( e , - (i s ] - [ Q e s - Q s ] ) 5 (( e s ] d1 + IZ  J X m s ( - e s - qs > q s d.         (16)

s = 1 t                                                                   s = 1 t+A

Положим теперь, что произвольная обобщенная сила Q s доставляет минимум целевому функционалу. Тогда при Л> 0 A m_s ( q g s - q_s 'y q_s = Z m s S q 2 >  0 . Поэтому необходимое и достаточное условие минимума целевого функционала 5 ² J > 0 выполняется когда

I: ^T+ J^Z [( V E s - V s ) 5 q s +X ( Q e s - Q s ) 5 (( e s ] d1 > 0.                                         (17)

s = 1 t

Поскольку в соответствии с принципом Гаусса траектории и скорости не варьируются, то интегрирование по

частям приводит к следующему выражению

n   Г dlQ.

I J

s = 1 t

dt ²

—

, -               n t+A t

X ^{- 1} Vs 5 qsd1 >I J   dQs-

ˆ

s = 1 t

dt ²

—

X ^{- 1} V_s 5 q_sd1 .

Значит

n z 5 = 1

d 2 Q ) dt ²

n

= r1 Z Vs,

5 = 1

t = ^t , q 5 = q 5^{( t} ), q 5 = q_s( ^t ),

t = t + A t, q 5 = q 5⁽ t + A t), q 5 = q 5⁽ т + A t).

Развертывание этого уравнения целесообразно производить для конкретных случаев задач структурного синтеза.

Структурный синтез терминальной системы управления . Пусть n = 1 и функция Гиббса имеет вид

1    1

g = ^ q²,                                                  (20)

тогда уравнения Аппеля записываются в следующей форме:

q = и, t0 = 0,q(t0) = -l, q(t0) = 0,

где U — управляющие силы.

Требуется синтезировать в аналитическом виде закон оптимального управления динамической системой (21), переводящий ее из начального состояния в состояние покоя из условия минимума целевого функционала:

t ₁

J = J dt ^ min ;

пусть 1 1 = 2,4 с.

В соответствии с (19) и (22)

q IV

= 0.

Решение этого уравнения имеет вид:

32      2

q = —— + — + Ct + D; q = —— + Bt + C;U = At + B.

62     2

Постоянные интегрирования определяются из краевых условий:

A = -1-3 [12( q (11) - q (0) - <7(0>ti) - 6 ti (^/(ti) - <7(0))]-

B = t-2 [6( q (t 1)- q (0)- <7 (0)t 1) - 211 ((11) - q(0))];

C = (0); D = q(0).

Исключение времени t 1 из (24) позволяет получить структуру закона управления как функции обобщенных

координат

6 A ² ( q - D ) + ( б ABC - 2 B. ³ ) 2 — ( <7 - C ) - ( 2 B ² - 6 AC )

Оценка эффективности предлагаемого решения проводится на основе сравнения с законом «мягкого» терми-

нального управления [2]

U ₌ ^{12 (} q ^{( t} 1 ^)- q ^{( t} )) _ ^{6 q ( t} 1 ^{)- 6 (} t ) ( t 1 - 1 ) ²               t 1 ^- t

Такое решение имеет особенность в конечный момент времени. В результате при приближении к конечному состоянию системы наблюдается эффект резкого увеличения равнодействующей сил Q . Данное обстоятельство хорошо

изучено и для борьбы с ним разработаны различные приемы устранения такой особенности [2, 19].

Результаты математического моделирования приведены на рисунках 1, 2. Здесь сплошной линией обозначены кривые, полученные с использованием (26), а пунктирной на основе (27).

Информатика, вычислительная техника и управление

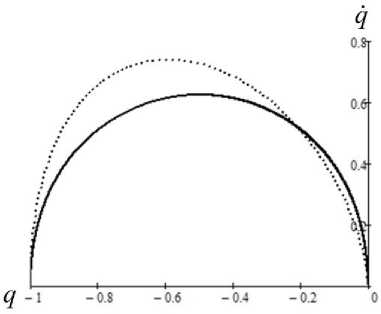
Рис. 1. Фазовый портрет

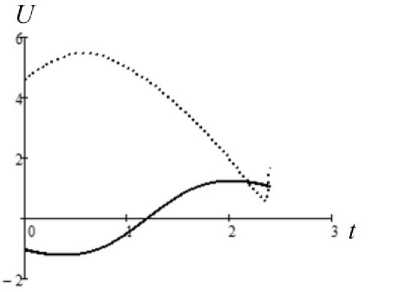
Рис. 2. Управляющие силы

Выводы . Получено новое необходимое и достаточное условие минимума целевого функционала, которое позволяет сводить задачу оптимального управления к краевой задаче для Аппелевой динамической системы. Его использование в случае линейной системы приводит к точному аналитическому решению. Это дает возможность выбора параметров регулирующего устройства. Результаты математического моделирования позволяют утверждать, что метод структурного синтеза терминальных управлений обеспечивает безударный режим изменения состояния динамической системы с минимальным объемом энергетических затрат в сравнении с решением из [2].