Структурный синтез устройства управления резервуарами

Необходимость применения резервуаров и резервуарных парков возникает на различных объектах хранения нефти и нефтепродуктов в процессе технологических операций. Резервуары и резервуарные парки являются технологическим объектами различных нефтеперекачивающих станций.

Существуют перекачивающие и промежуточные станции. На промежуточных станциях резервуары являются буферными емкостями и предназначаются для компенсации неравномерности подачи двух соседних перекачивающих станций. На перекачивающих станциях резервуарные парки предназначаются для хранения (резерва) нефти и нефтепродуктов. При некоторых плановых или аварийных остановках одной из промежуточных станций транспортируемая жидкость поступает в резервуарный парк этой станции, а следующая станция продолжает работать за счет нефти и нефтепродукта, имеющегося в ее резервуарном парке.

Резервуарный парк имеет конические виды резервуаров и является объектом со сложнейшей структурой. Управление таким резервуарным парком является интересным как в теоретическом плане, так и в практическом.

Рассмотрим задачу синтеза системы управления расходом смеси химического объекта (рис. 1), состоящего их трех конических резервуаров со свободным истечением жидкости из общего трубопровода, соединяющего выходы резервуаров [1; 2]. В резервуары жидкости поступают по двум каналам питания, при этом одна жидкость подается в первый и второй, а другая - в первый и третий резервуары. Управление уровнями жидкостей во втором и третьем резервуарах производится изменением потока жидкостей по первому ( u i ) и второму ( U 2 ) питающим трубопроводам. Расход жидкостной смеси на выходе определяется уровнем жидкости во втором резервуаре.

Рис. 1. Функциональная схема объекта управления.

Состояние объекта управления в пространстве фазовых переменных описывается следующим обыкновенным нелинейным уравнением

<

■          з a3 xi(t) =--2 f (xi - X2) +     2(U1 + U2);

n x j

■ x2 (t) = —т [ f (Xi - x2) - f (x2 - x3) - f (x2)] + —-2 nx22nx

3 a x3(t)       2 J (x2   x3) +n 2 U2);

nx32nx

U i ;

где f (x; - x}) = ^2g | x; - xi+j |sign(x - xi+J ; x1, x2, x3 - соответственно уровни жидкостей в первом, втором и третьем резервуарах, y = а2gx2 - расход жидкости на выходе объекта.

Требуется определить законы управления u 1 и и 2, обеспечивающие заданные уровни жидкостей во втором и третьем резервуарах и, следовательно, заданный расход жидкости на выходе, т.е.

x ₂

= x =     ;

^{2 r}   2 ga ²

^х з = ^х з r = y r ;

x l _r   1,^{25 x} ₂ r ;

В установившемся режиме, согласно (1), выполняются следующие соотношения [1; 2]:

^{f (}x l r - x 2 r ) = ^{0,5 f (} x 2 r ),   a^{f (x} 2 r ) = u l r + u 2 r = У 1 r ,   a^{f (} x 2 r - ^X 3 r ) =^— 0^,5u 2 r ^.      (3)

По заданному X 2r (2) из (3) можно найти x ir - уровень жидкости в первом резервуаре в установившемся режиме работы объекта. Отличительной особенностью объекта (1) является присутствие управлений u i и U 2 во всех строках правых частей дифференциальных уравнений. Согласно [1], управление u i и U 2 всегда можно синтезировать так, чтобы обязательно обеспечить требуемые соотношения (2).

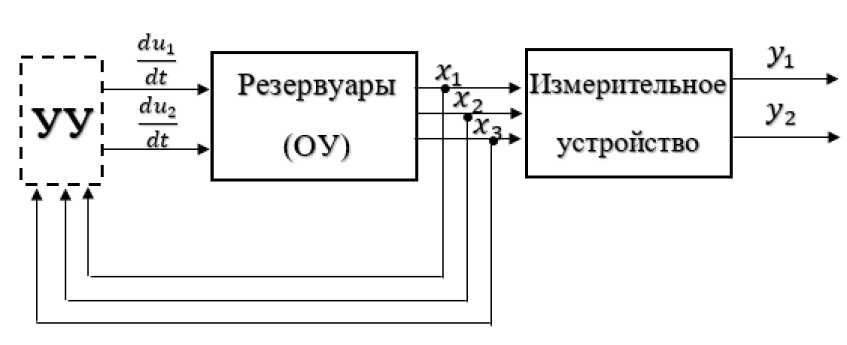
Рис. 2. Структурная схема САУ.

Рассмотрим нелинейный многомерный объект управления, состояния которого описывается следующим нелинейным векторным дифференциальным уравнением [3]:

^x i (t) = ^f i ^[x(^t)^,u(t)^,^ (t) Лк ^x i ^(t o ) = ^x io , i = ^1,n, t e [t o ,t k ^], (4) где: ^x(t) = ^{[ x} i ^(t),X 2 ^(t), ... ^,X n ^{(t) J T} - вектор переменных состояния или вектор фазовых координат объекта управления; u(t) = [ u₁(t),u₂(t),...,u_m(t) J ^T — вектор управления (управляющих или регулирующих воздействий); f(x, u) = f(x, u, ^, t)= [ f₁ (x, u, ^, t), f 2 (x, u, ^, t),...,f n (x, u, ^, t) J T - n-мерная вектор-функция, удовлетворяющая условиям Коши; ^(t)= [ ^₁ (t),^ ₂ (t),...,^ _r (t) J T - _вектор возмущающих воздействий.

Будем считать, что объект (4) является полностью управляемым и необходимо стабилизировать его нулевое состояние. Основными показателями качества регулирования будем считать динамическую и статическую точность, а также быстродействие системы управления. Обозначим через граничные положительные функции ojt), с помощью которых задаются границы допустимых областей. Переходные процессы по ошибке управления (невязки) e1 (t) определяют предъявляемые требования к качеству процессов управления синтезируемой системы. Степень достижения цели управления или

регулирования

gi(t)

характеризуется вектором невязки

e(t)=g(t) - x(t)-

Математическое описание такого инженерного критерия можно задавать на основе следующих модульных неравенств:

|xi ^(t)| = |^e(t)| <^ ^(t), t G [^t o, t_k],    i = 1,П,                           (6)

где q (t) — положительные, непрерывно-дифференцируемые функции, определяющие точность и быстродействие проектируемой автоматической системы.

Задача управления формулируется таким образом: для управляемого или регулируемого объекта, состояния которого описываются векторным нелинейным дифференциальным уравнением (1), необходимо определить структуру и параметры автоматического регулятора, обеспечивающего выполнение точности и быстродействия проектируемой системы, т.е. качества процесса управления.

Для достижения желаемого качества переходных процессов закон управления u(t) должен обеспечивать выполнение неравенств (6). Один из возможных путей достижения желаемого качества состоит в задании определенных условий для функций f i [x(t), u(t), ^ ( t),t] . При этом такие условия должны обеспечивать параметрическую разрешимость соотношений (2), также определение структур и параметров алгоритмов управления.

Желаемую динамику САУ зададим в виде векторного дифференциального уравнения x (t) = f * (x,p),                                            (7)

где f * = [ f₁ * (x,p₁), f₂ * (x,p₁), _ ,f_n * (x,p_n) ] ^T - n-мерная, в общем случае нелинейная вектор-функция; Р = [pi^/^pJ — r — мерный вектор-параметр, подлежащий выбору так, чтобы решение x(t) системы (16) удовлетворяло условиям заданного качества управления (6).

В результате введения понятия желаемой динамики для проектируемой замкнутой системы, искомый закон управления u(t) целесообразно определить из условия близости соответствующих компонентов вектор-функций f(x,u) и f (x,p) с требуемой точностью. В частности, эти условия целесообразно задавать в виде модульных неравенств:

fi [ xCXuGO^t] —  f* [ x(t),p]< Si (t), i = l,n, t e[to ,tk ],                     (8)

где 5j(t) - функции, которые задают точность приближения, они положительные и непрерывно дифференцируемые.

Таким образом, процедура синтеза регулятора для многомерного нелинейного объекта состоит из двух этапов:

• 1)    описание подмножества P * и определение вектор-параметра p е P ;

• 2)    нахождение закона управления u ( x , t ) , обеспечивающего выполнение условий (8). Введем функцию

F (x,u) = f (x,u,£,t) - f * (x,p), i = 1,n,(9)

Тогда неравенства (8) запишутся в виде

I Fi (x,u)^s i(t),         i =1,n,      t е [to,tk].

где F(x,u) = [^ (х,и),^(х,и),...,^(х,и) ] ^T.

Тогда уравнение динамики многомерного регулятора имеет вид [3]:

U(x,t) = L•[ Y{ f(x, u, £ , t) - f*(x,p) } - Z• f(x,u) - H• ^(t)].(11)

где Y = [yj  Y2--- Yn]T ={ Yiv }nxn — вещественная матрица, составленная из n-мерных векторов

Y i = ^[ Y ii , Y 12 , - , Y in ^] ,   Y 2 = ^[ Y 21 , Y 22 , - , Y 2n L Y n = ^[ Y ni , Y n2 , - , Y nn ^] .

где функциональные матрицы

~ fsf ]          [df ][5

z = 1 —- r , m = 1 —- f , h = 5 —- r d x.         P uv         P £vl/

I jnxn                v > n*m          I ~v J nxr а матрица Y= { Yiv }nx - вещественная матрица, составленная из настроечных параметров уу системы; в предположении что существует обратная матрица w-i = [mt • m]^.

где матрица L=W-i MT. Если вектор-функция f (x,p) задается в линейной форме, т.е.

f*(x,p) = P • x(t),(13)

где P = { pjj }_nx - вещественная n x n матрица, то тогда закон управления (11) имеет вид [3]

u(x,t)= L •[ Y •{ f(x, u, £ , t) - P • x(t) } - Z • f(x,u) - H • ^(t) ].

Обобщенная структура системы управления, включающая динамический нелинейный регулятор с законом управления (14), показана на рисунке 3.

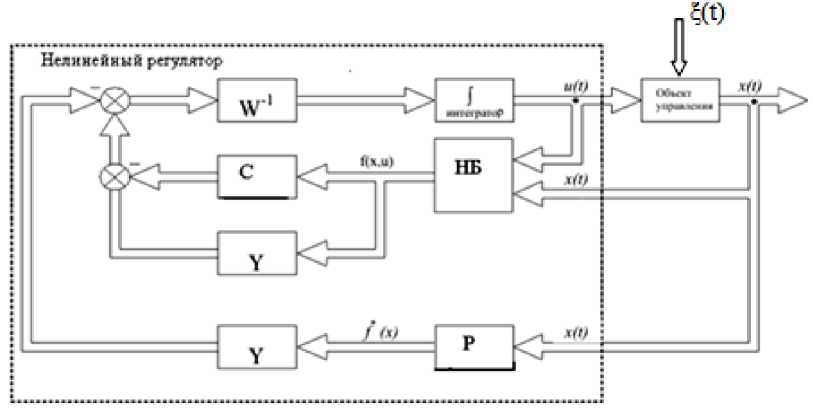
Рис. 3. Обобщенная структура САУ.

На основе прикладного пакета программирования MATLAB в автоматизированном режиме были получены алгоритмы управляющих воздействий, выведены графики уровней нефти в резервуарах, а также выходные переменные группы резервуаров. Управляющие воздействия на объект управления имеют следующий вид:

du1 =(p(x12(x1)2))+(2x22(x2)2)/(3(x1)2) - (2px22 (x2)2)/(3(x1)2))(l15)/(2px12)-l11 /(px12)l15 /(px13) - l11 dt

/(px 1 ² ) +2l 11 /(px 1 ³)-l 12 /l 16 +l 15 /(2px 1 ²)+l 11 /(px 1 ²)(p 22 +l 14 /(px 1 ²))+l 12 /l 16 +g 22 (l 15 )/(2px 1 ²)-p 22 x 2 +(l 11 / (px 1 ²))-(p(x 1 ²(x 1 )²+2x² 2 (x 2 )²))/(3(x 1 )² ) -(2px² 2 (x 2 )²)/(3(x 1 )²))(l 14 )/(px 1 ²)+l 12 /l 16 (l 15 )/(2px 1 ²)+ (l 11 /(px 1 ²))+g 11 (p 11 x 1 - (3(u 1 +u 2 )) /(2px 1 ²)+(l 11 /(px 1 ²))-(l 15 )/(2px 1 ²) - (l 11 /(px 1 ²))(p 11 +l 15 )/(px 1 ³) +l 14 px 1² )-2l 11 /(px 1³ )+l 11 /l 16 - (2px ²2 (l 15 ))/(2px 1² )+l 11 /(px 1² )((3u 1 )/(px ³2 ))+(2al 11 + 2sign(x 2 -x 3 ) (l 18 )-  2sign(x 2 )(l 19 )/(px³ 2 )+(3a  2sign(l 19 )+  2sign(l 17 ) - (  2sign(l 18 )+l 12 /(2l 17 -l 13 /l 15 +

( 2gsign(x₂) sign(x₂))/(2(l₁₉))/(px²₂)+((3u₁)/(2px²₂))+l₁₁+ 2sign(x₂ - x₁) (l₁₈)-  2sign(x₂)

(l₁₉)/(px²₂))(p₃₃+(3a 2sign(l₁₈)+l₁₃/l₁₅/(px²₂)))+g₃₃((3u₁)/(2px²₂))-p₃₃(x₃)+l₁₁+( 2sign(x₂ -x₃)) (l 18 ) - 2sign(x 2 )(l 17 /(px² 2 ))-l 14 +3l 12 /(2(l 17 )((3(u 1 -u 2 ))/(2px 1 ²)))-(l 11 /(px 1 ²))/(px² 2 ))/3.

dU =((n(x 2 (X 1 )² +2x 2 (x ₂ )² ))/(3(Х 1 )² )-((2nx 2 (x 2 )² )/(3(X i )² )(l i5 )/(2nx 2 )-l„ /(nx 2 )(l i5 )/ (nx )-1 ,4 /(nx 2 )+(2(1 ,, ))/(nx 3 )-1 ,2 /1 16 +1 ,, /(2nx 2 )+1 ,, /(nx 2 )(p₃₂ +L /(nx 2 )+l_n /(2nx 2 (1 ,, )+ g₂₂sign(l₁₅ )/(2nx 2 )-p₂₂ (x ₂ )+1„ /(nx , ² ))-(n(x 2 (x , )² +2x 2 (x ₂)² ))/(3(x , )² )-(2nx 2 (x ₂ )²)/ (3(x , )² (1 ,4 )/(nx 2 )+(1 ,2 )/(2nx 2 (I ,, )(1„ )/(2nx 2 )+1 ,i /(nx 2 H, /(2nx 2 И, /(nx , ² )(p ,, +1 ,, / (nx 3 ))+1_M/(nx 2 )-(2(1„)/(nx 3 ))+1 ,2 /(2nx 2 (1 ,7 Я+д^длфДх.НЛ^^ ) +1_n/(nx 2 )) ^-(2nx 2 ⁽¹ ,₅ ^)/(2nx 2 ⁾⁾⁺⁽¹„ /( ^nx ■ ⁾⁾⁽⁽³ U 1 ^)/(nx 2 )l( ² (l ⁾ +_л/2si ^g n(x 2^ x 3) ⁽¹ 18 ) ^-7 2sign ^(x 2 ) ⁽¹ ,7 ^)/(nx 32 ⁾⁺¹ ,4 ⁺л/² Sign ⁽¹ 17 ^)-7 2sigД ⁽¹ 18 ⁾⁺¹ ,2 ^/(21 , ₇ ^-1 ,3 ^/2(1 ,8 ⁾ + ⁽7^2gSig n ^(X 2 ^)Si gn ^(X2 ^ ⁽²⁽¹ ,9 ^)/(nx 2 ^))+((3U! ^)/(2nx 2 Ж , ⁺V² Sign ^(x 2 - ^x ) ⁽¹ ,8 ^)- 7 ^2si gn ^(x 2 ⁾⁽¹ ,9 ^)/(nx 2 ⁾⁾⁽ p₃₃ ⁺

(3a(72sign(li8 )-li3 /(2(1 )ях2 ))+g33sign((3Ui )/(2nx2 )-p33x3 +ln +/2sign(x2-x)(li8) "A/2sign(x2Xli9)/(nx2)) — 114 +G/2gsign(sign(xi — x2Xxr X2)))/(2(li7))(L)/((2nx2) - 111 /(nx2 ))/(nx 2 )/3, где l11 =(3 2asign (x1-x2)  g|(x1-x2) ; l12 =(3 2agsign·sign(x2 -x3)(x2 -x3));

l13 = 2gsign(sign(x2 -x3 )(x2 -x3 )); l14 =(3 2asign (g|(x1-x2)|));

li5 =(3(ui +u2 ));li6 =(2nx2 G/gKxi-x 2 )D); li7 =^(gKxi -x 2 Ж l18=  (g|(x2-x3)|);l19= (g|x2|).

Результаты моделирования продемонстрированы на рисунках 4, 5, 6, 7.

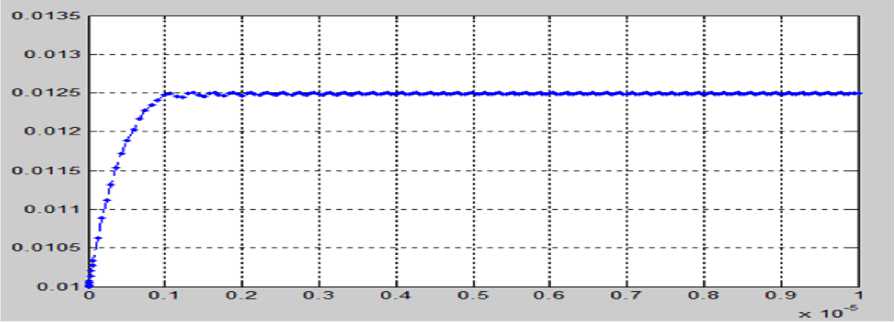
Рис. 4. Уровень жидкости 1-го резервуара x 1 =x 1 (t).

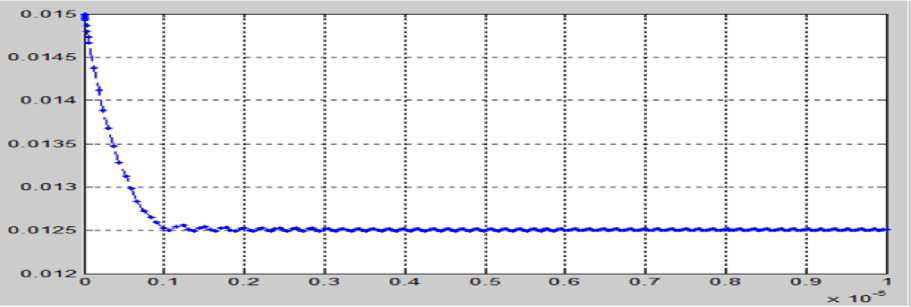
Рис. 5. Уровень жидкости 2-го резервуара x 2 =x 2 (t).

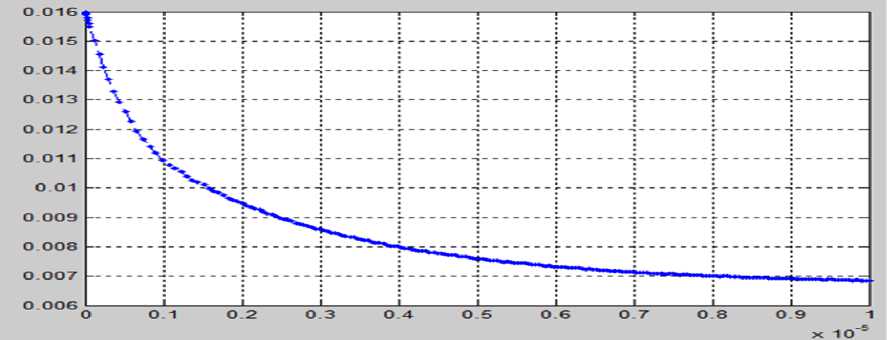
Рис. 6. Уровень жидкости 3-го резервуара X 3 =X 3 (t)

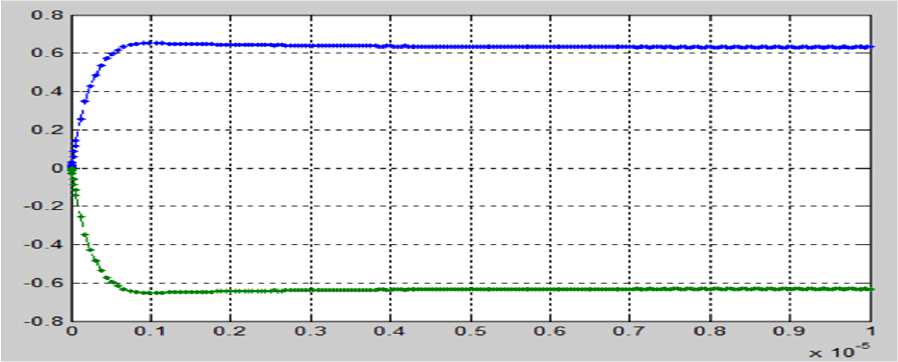
РИС. 7. ПОТОК ЖИДКОСТеЙ U 1 =U 1 (t) И U 2 =U 2 (t).

В данной статье были рассмотрены общие сведения о резервуарах, используемых в нефтегазовой промышленности. В ходе исследования нам удалось выяснить, что автоматизация конического резервуарного парка позволяет увеличить пропускную способность парка, а также повышает качество управления процессом перекачки нефти. Далее были произведены некоторые технологические расчеты.

Таким образом, был разработан алгоритм управления резервуарами на основе метода структурного синтеза, представленного в [3]. На основании постановки задачи исследования использовано математическое описание в виде системы дифференциальных уравнений для трех резервуаров [1; 2], которые описывают состояние каждого резервуара, а также разработано программное обеспечение для реализации поставленных задач.