Students Classification With Adaptive Neuro Fuzzy

Published Online July 2012 in MECS

Predicting students’ academic performance is critical for educational institutions because strategic programs can be planned in improving or maintaining students’ performance during their period of studies in the institutions[1].

Arithmetical and statistical methods are unable to offer an effective inference procedure to perform the evaluation of the academic performances of students in a more natural way, using linguistic variables. This method might help students, their parents, decision makers, and evaluators in obtaining more reliable and understandable results for a student’s achievement, or for a group of students and their comparative evaluations. It is important to point out that the aim of proposed method is not to replace the traditional method of evaluation; instead, it is to strengthen the present system by providing additional information for decision making [2].

Assessment of the student’s academic performance (SAP) is one of the most important practices used for three main reasons: to decide on pass and failure in courses, to obtain an indication of the student’s level of learning, and to provide information on the effectiveness of teaching. In traditional (statistical) methods, the student’s academic performance (SAP) is evaluated based on the marks collected by a student. It can be classified into numerous categories such as single numerical scores usually referring to 100 percent, single letter grades (e.g. A, B, C, D, or F), nominal scores (e.g. 1, 2, 3. . .10), linguistic terms such as ‘‘Fail”, or ‘‘Pass” or single gradepoints from 0.00 to 4.00. As a part of this study, a weighted sum of assessment tools is used to calculate the numerical score of each student as follows:

Quiz (Q) is 10%, Major (M) is 15%, Midterm (MD) is 20%, Final (F) is 40%, Performance Appraisals (P) is 10%, and Survey (S) is 5%. The total out of 100 indicates the student’s academic performance(SAP)[2].

A number of socio-economic, biological, environmental, academic, and other related factors that are considered to have influence on the performance of a university student were identified. These factors were carefully studied and harmonized into a manageable number suitable for computer coding within the context of the ANN modeling[3].

The paper is organized in five sections. After the introduction in Section І, Section ІІ, which also introduces the existing methods of the performance evaluation. Section ІІ continues with explanations of Lvq neural network and adaptive neuro-fuzzy systems (ANFIS) in section ІІІ. Section ІV discusses the factors affecting on classification student base learning . It continues with discussions on the architecture of hybrid learning and fuzzy model validation and lvq neural network, the error of observations for training data sets. Section V presents the conclusions of the research. The paper ends with a list of references.

• II.    Literature review

Neuro-fuzzy systems are one of the most successful and visible directions of that effort. Neuro fuzzy hybridization is done in two ways [4]: a neural network equipped with the capability of handling fuzzy information (termed fuzzy neural network) and a fuzzy system augmented by neural networks to enhance some of its characteristics like flexibility, speed, and adapt-ability (termed neuro-fuzzy system(NFS) or ANFIS). An adapted neuro-fuzzy system (NFS) is designed to realize the process of fuzzy reasoning, where the connection weights of network correspond to parameters of fuzzy reasoning[4,5]. These methodologies are thoroughly discussed in the literature [4].A second and distinct approach to hybridization is the genetic fuzzy systems (GFSs) [6]. A GFS is essentially a fuzzy system augmented by a learning process based on genetic algorithms (GAs). The parameter optimization has been the approach used to adapt a wide range of dissimilar fuzzy systems,as in genetic fuzzy clustering or genetic fuzzy systems [6].However, genetic fuzzy systems are not subject of this work.

Let's review educational productivity theory first. In 1981, Walberg [7] specified a model for educational productivity in which nine factors were identified that promote student learning. These nine factors were later grouped in three sets. The first set indicates a student's aptitude-attributes. The second set of factors indicates those instructional aspects which affect student learning and achievement, namely the quantity and quality of instruction. The last set of factors consists of the social-psychological environment, which includes the educational environment, the home environment, and the peer environment, as well as exposure to mass media.

In 1954, the University of New Zealand Council for Educational Research investigated the relationship between academic standards of students on entrance and their first year university work. The study found that the median correlation found among the many sets of variables representing general school performance and general university performance was indicated by a tau coefficient of 0.36 for the first year students undertaking their studies on afull time basis (Maidment ,1968). In 1975, Bakare summarized the factors and variables affecting students performance into the intellective and non-intellective factors, emphasizing that the intellectual abilities were the best measure [8]. He categorized causes of poor academic performance into four major classes:

• 1)    Causes resident in society

• 2)    Causes resident in school

• 3)    Causes resident in the family

• 4)    Causes resident in the student.

Studies such as [9] and [10] looked at a more general aspects of success while Anderson et al., 1994 studied the effect of factors such as gender, student age, and students’ high school scores in mathematics, English, and economics, on the level of university attainment. According to their study, students who received better scores in high school also performed better in university. Another aspect discovered was that men had better grades than women and choose to drop from school less often.

Adedeji sought to find out concluded in his research that there exists a positive relationship between students admission scores and their undergraduate performance [11].

Neural Networks (NN) have been used by many researchers in solving problems requiring classification and function approximations [12].

Byers and DesJardins [13] reported the first to attempt to use ANNs in predicting enrollment rates, i.e. which students were likely to be enrolled in a 4-year institution. More relevant to our task at hand is the recent work by Barker et al. [14]. They reported the use of ANNs and Support Vector Machines for classifying successful student graduation rates at a 4- year institution. They used 59 parameters that included demographic, academic, and attitudinal information to describe each student.

Merry McDonald, Brian Dorn and Gary McDonald [15] used statistical analysis to analyse students’ performance in online computer science courses compared with a traditional classroom approach. Two methods were used, simple comparison of means and regression analysis. Inputs for that analysis are final scores, final letter grades, number of total credit hours completed and cumulative GPA. T-tests show that on ground database students significantly outperformed online students. Bijayananda and Srinivasan [16] used neural networks to predict MBA students’ success. They predicted the students’ performance for admission decisions by using neural network to classify applicants into successful and marginal student groups based on undergraduates GPA, GMAT scores and other relevant dat.

In [17], a fuzzy rule based system has been proposed that constitutes a set of 18 fuzzy rules used in assessing student’s performance and learning efficiency obtained from experts. Assessment takes four input factors which are average marks, time spent, number of attempts and help needed.Combining it together with the existing fuzzy system may lead to the application of ANFIS (Adaptive Neuro-Fuzzy Inference System.

Osman taylan , bahattin karagozoglu provide an adaptive neuro –fuzzy model for prediction of students academic performance. The input attributes of the ANFIS system was the assessment tools that are Quiz (Q), Major (M), Midterm (MD), Final (F), Performance appraisals (P), and Survey (S)’ and the output is the ‘Student’s Academic Performance (SAP)’[2].

Neuro-Fuzzy has been used in various areas, such as emotion recognition [18], control engineering [19], decision support systems [20], civil engineering [21], etc. Fuzzy Systems and Neural Networks are efficient and effective methods to analyze the uncertainty in education assessment. For instance, Neural Networks have been used by many researchers in solving prediction problems which require function approximations [22] and Fuzzy Systems have been used in application of education assessment [23 – 27].Sadique used it in his work on student modeling [28].Anfis uses fuzzy inference of Sugeno type [29].

Fuzzy set theory is an efficient and effective method to represent the uncertainty and fuzzy terms in the assessment environments. Nolan in [30-31] has shown that an Expert Fuzzy classification scoring system can help teachers in making assessment in less time and with a level of accuracy comparable to the best teacher graders. Ma and zhou in [32] proposed a fuzzy grade scale approach to assess and evaluate the outcome of studentcentered leaming. Echauz and Vchtsevanos [33] presented a fuzzy grading method that utilizes student performance measures to produce a fair mark distribution. Rantjt [34] described a fuzzy set to evaluate the student's answer script.

• III.    Study Objectives And Method

The objectives of this study are: 1) to transform suitable factors that affect a student’s performance into forms suitable for an adaptive classification system, and 2) to model an Artificial neural network , adaptive neural fuzzy system that can be used to predict a candidate’s performance based some given pre admission data for a given student.

• A.    Neural Network

Developing a neural net solution means teaching the net a desired behavior. This is called the learning phase. Either sample data sets or a “teacher” can be used in this step. A teacher is either a mathematical function or a person that rates the quality of the neural net performance. Since neural nets are mostly used for complex applications where no adequate mathematical models exist and rating the performance of a neural net is difficult in most applications, most are trained with sample data.

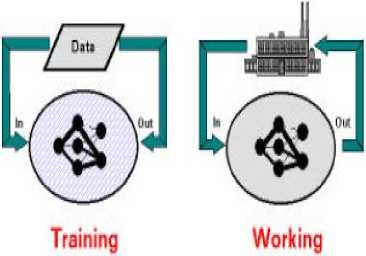
Figure 1. Training and working phase for supervised learning

A.1 Competitive Learning

The neurons in a competitive layer distribute themselves to recognize frequently presented input vectors.

A.2 Architecture

The architecture for a competitive network is shown fig.2.

The box ||dist|| in this figure accepts the input vector p and the input weight matrix IW1,1, and produces a vector having S1 elements. The elements are the negative of the distances between the input vector and vectors iIW1,1 formed from the rows of the input weight matrix.

The net input n1 of a competitive layer is computed by finding the negative distance between input vector p and the weight vectors and adding the biases b . If all biases are zero, the maximum net input a neuron can have is 0. This occurs when the input vector p equals that neuron’s weight vector. The competitive transfer function accepts a net input vector for a layer and returns neuron outputs of 0 for all neurons except for the winner , the neuron associated with the most positive element of net input n 1. The winner’s output is 1. If all biases are 0, then the neuron whose weight vector is closest to the input vector has the least negative net input and, therefore, wins the competition to output a 1.

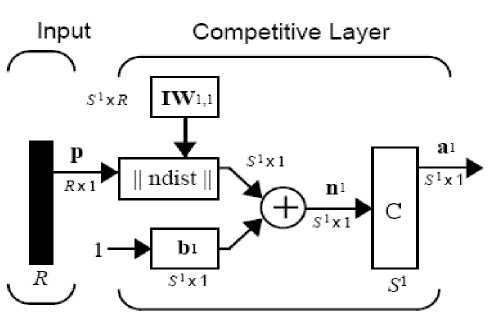
Figure 2. architecture for a competitive network

A.3 Kohonen Learning Rule

The weights of the winning neuron (a row of the input weight matrix) are adjusted with the Kohonen learning rule. Supposing that the ith neuron wins, the elements of the ith row of the input weight matrix are adjusted as shown below.

^'.«.1|«'-,.,-|.....,$.-1|«и.,-|.. (1)

The Kohonen rule allows the weights of a neuron to learn an input vector, and because of this it is useful in recognition applications[35].

Thus, the neuron whose weight vector was closest to the input vector is updated to be even closer. The result is that the winning neuron is more likely to win the competition the next time a similar vector is presented, and less likely to win when a very different input vector is presented. As more andmore inputs are presented, each neuron in the layer closest to a group of input vectors soon adjusts its weight vector toward those input vectors. Eventually, if there are enough neurons, every cluster of similar input vectors will have a neuron that outputs 1 when a vector in the cluster is presented, while outputting a 0 at all other times. Thus, the competitive network learns to categorize the input vectors it sees.

A.4 Lvq Network architecture

Lvq hybrid network composed of both types of learning with supervisor and without supervisor. InLvq network, each neuron in the first layer is assigned to one class, and then, each class is assigned to a neuron in the second layer.

A.5 Lvq Learning Rule

InLvq network, competitive learning accompanies supervision lvq learning rule is done as follows:

In each repitition, a P input vector is applied to the network, and then the distance between P vector and any sample vectors, represented by the w ¹ columns, will be measured. Neurons of the middle layer compete with each other. The output of the winner neuron in i ^* will be 1, and of others, 0.

a ¹ = 1

i

_ a =0 ⁰    У * * *

Then, to obtain a \ a¹ are multiplied in w2 matrix. a ² has only a non-zero element, for example j ^* , that implies the p input vector belongs to j ^* class. Then, to set the middle layer parameters of lvq network, Kohnen learning rule is used in the form of 3 and 4 relationships [35]:

a) If a■ * = t■ * ( k + 1) = 1

1                1 Г 1

W_x 1 ( k + 1) = w ^ ( k ) - a ( p ( k + 1) - w1 ( k ))

This means that p vector has not been correctly classified, so we know that the hidden neuron won the competition wrongly; therefore, the weight vector of i ^* neuron W 1 , gains distance from the p input vector.

• B.    Designing by neuro fuzzy

  • B.1    Neuro Fuzzy

    It immediately comes to mind, when looking at a neural network, that the activation functions look like fuzzy membership functions. Indeed, an early paper from 1975 treats the extension of the McCulloch-Pitts neuron to a fuzzy neuron (Lee & Lee, 1975; see also Keller & Hunt, 1985).

The one neuron in the output layer, with a rather odd appearance,calculates the weighted average corresponding to the center of defuzzification in the rule base.Backpropagation applies to this network since all layers are differentiable. Two possibilities for learning are apparent. One is to adjust the weights in the output laye,i.e ,all the singletons wi until the error is minimized. The other is to adjust the shape of the membership functions, provided they are parametric.also rule weight can be changed with training data.in Neuro fuzzy model is not necessary output be linear[36].

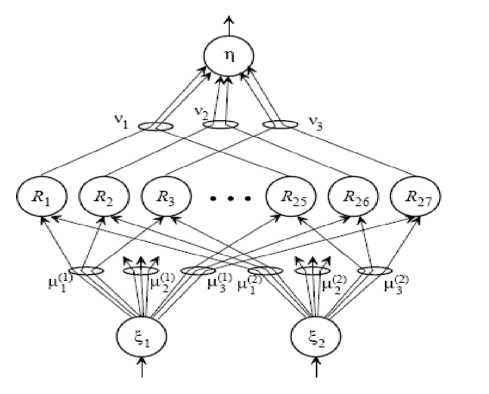
Figure 3. Neuro fuzzy model control system

• B.2    Sugeno Model

A typical rule in a Sugeno fuzzy model has the form. If Input 1 = x and Input 2 = y , then Output is z = ax + by + c.

For a zero-order Sugeno model, the output level z is a constant (a=b =0).

The output level zi of each rule is weighted by the firing strength wi of the rule.For example, for an AND rule with Input 1 = x and Input 2 = y, the firing strength is wi =AndMethod (F1(x), F2(y)) ;where F1,2 are the membership functions for Inputs 1 and 2. The final output of the system is the weighted average of all rule outputs, computed as:

{( xk, yk ), k = 1,..., K }

where x^k refers to the K-th input pattern, then we have:

Final Output

N

2 w z i

= 1

N

2 w i i =1

A Sugeno rule operates as shown in the following diagram(fig.4)

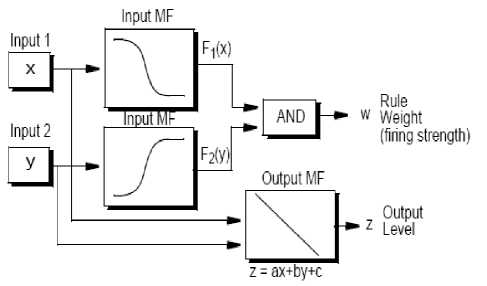
Figure 4. Sugeno model

(1,0) if X k belongs to class 1 (8)

(0_,1)   if x ^k belongs to class 2

The error function for K pattern can be defined by relationship 9:

E_k = "[( °1 — yk )2 + ( Ok — У 2 )2]             (9)

where yk is desired output, and Ok  is computed output.

k y = 1

ANFIS (Adaptive Neuro Fuzzy Inference System) is an architecture which is functionally equivalent to a Sugeno type fuzzy rule base (Jang, Sun & Mizutani, 1997;

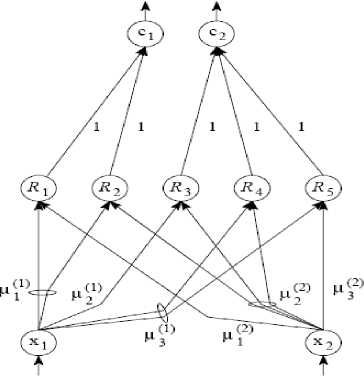
Figure 5. adaptive neuro fuzzy Network(anfis)

B.3 Anf s Classf er

Consider the fuzzy neural network in figure 4. The output of the first layer nodes are the degree of membership of linguistic variables. Typically, in this layer bell –shaped functions are used. Bell-shaped function is shown in Relationship 10. The purpose of learning in this layer is adjusting the parameters of membership function of inputs.

—

f ⁽ x ) = exp

x

—

( 2

b

a

1 ₎2

The second layer is 'rules layer'. In this layer, the condition part of rules is measured by usually Min fuzzy logic operator, and the result will be the degree of activity of rule resultant. Learning, in this layer, is the change of the amount of activity of rules resultant, regarding to the 'training data', given to the network. In the third layer, we'll get the linear combination of rules resultant rate, and in order to determine the degree of belonging to a particular category, Sigmund function is used in layer 4 [37]. If a series of training vectors is given to the network in the form of the formula 7:

• IV. Design Classification System

In this study, we took into 34 factors. Then, we have created the linguistic variables corresponding to the values . Output is categories of students to 5 Very weak, weak, moderate, good, excellent.

34 factors affecting learning as follows[38]:

• A.    age

• B.    Family

bl: level of parents' education: master or Ph.D., bachelor, senior high school, junior high school , elementary school , illiteracy b2: level of parents' socio-economic status: very high,high, moderate, low, very low

• C.    Previous knowledge:

cl: level of arithmatic score: top 20% , top 20%-40% , top 40%-60% , top 60%-80%, top 80%-100% c2: level of physics score: top 20% , top 20%-40% , top 40%-60% , top 60%-80%, top 80%-100%

• D.    Educational psychology:

dl: level of self-efficacy: top 20%, top 20%-40%,top 40%-60%, top 60%-80%, top 80%-100% d2: level of concept of course usefulness: very high,high, moderate, low, very low d3: level of interest: very high, high, moderate,low, very low d4: level of academic self-confidence: very high, high, moderate, low, very low d5: level of expected grade: very high, high, moderate, low, very low

• E.    Learning style:

el: level of adaptive learning strategy: very high, high, moderate, low, very low e2: level of self-discipline: very high, high, moderate, low, very low e3: level of class attendance: 100%-90%, 90%-80% , 80%-70% , 70%-60% , 60%-50%, 50%-40% , 40%-30% , 30%-20% , 20%-10% , 10%-0% e4: amount of time students engage in learning: 10 above, 10-9, 8-7, 6-5, 4-3, 2-1, 0

• F.    Instruction:

fl: level of clarity of instructor presentations: very high, high, moderate, low, very low f2: level of instructor's personality: very high, high, moderate, low, very low f3: level of repetition of parts of the instruction for clarification: very high, high, moderate, low, very low f4: level of student-teacher interactions: very high, high, moderate, low, very low f5: level of encouragement from instructors: very high, high, moderate, low, very low f6: level of stress from instructors: very high, high, moderate, low, very low

• G.    Teaching material:

g 1: level of course difficulty: very high, high, moderate, low, very low g2: level of test-anxiety: very high, high, moderate, low, very low g3: level of match between instructor presentations and exam content: very high, high, moderate, low, very low g4: level of match between homework and exam content: very high, high, moderate, low, very low g5: level of classroom environment: very high, high, moderate, low, very low

• H.    Peer:

h1: level of classroom climate: very high, high, moderate, low, very low h2: level of collaborative learning: very high, high, moderate, low, very low h3: level of peer competition: very high, high, moderate, low, very low

• I.    Non-academic leisure-time behavior:

• il:    level of activities outside school: very high, high, moderate, low, very low

• i2:    level of exposure to Internet : very high, high, moderate, low, very low

• i3:    level of exposure to television: very high, high, moderate, low, very low

  We implemented Our proposed system at the Institute Fakhruddin As'ad Gorgani for 71 student Entering in 1389. To implement article matlab 7.1 were used.

• V. Discussion and Conclusion

In anfis system number of membership function of each factor 5, function type primf, output membership function linear,fis type gride partition and optima. method type 34

hybrid Were considered. 5 rules a weight was created. After training by training data, network with 20 epochs the root mean squared errors value(rmse) reaches 0.1348(fig6).

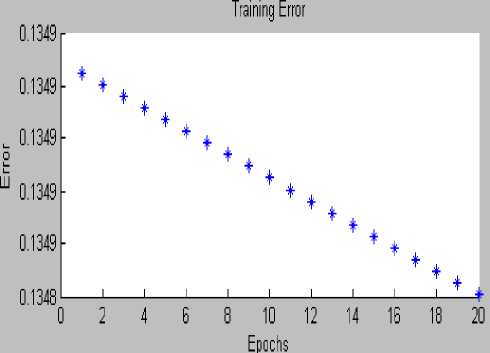
Figure 6. Anfis root mean squared errors

In the same conditions using neural networks lvq with 5 neurons in output layer ,10 neurons in competitive layer ,learning rate 0.01 and number 20 epoches the root mean squared errors value reaches 0.2374 (fig7). Also, in the same conditions using neural networks lvq with 5 neurons in output layer ,5 neurons in competitive layer ,learning rate 0.01 and number 20 epoches the error value was 0.2374 (fig8). Anfis proposed system rmse is less , Thus it can be used in student classifying as a human expert in operational environment.

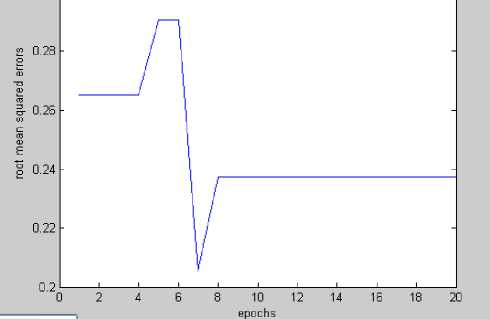
Figure 7. Lvq root mean squared errors

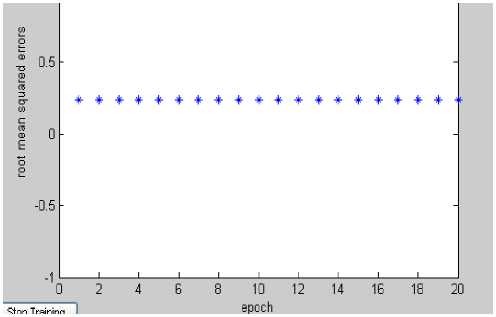
Figure 8. Lvq root mean squared errors 5, 5 neurons in competitive layer

For future work can be other factors such as Intelligence Quotient (IQ) tests , different types of membership functions, different types of neural network and optimization algorithms like genetic algorithm considered.

Therefore, the intelligent planning system (INPLANS) should be able to help the academic advisory in generating a planning based on the student’s performance.

The advantage of Neural Networks is it has the learning capability to adapt new data. On the other hand, Fuzzy Systems has the capability to handle numerical data and linguistic knowledge simultaneously.

There are two main motives behind wing fuzzy logic. First, when the definition of the problem is vague and uncertain. Second, for a class of applications that are well defined but the solution is not, the tolerance for imprecision can be exploited to simplify the solution.A typical task of the fuzzy data analysis is to discover rules in large set of data. The rules found can then be used to describe the dependencies within the data and to classify new data.

Acknowledgments

This work received support from the Department of Computer Engineering, Islamic Azad University, sari Branch.