Study of 2D DOA Estimation for Uniform Circular Array in Wireless Location System

Published Online December 2010 in MECS

Wireless communication has enjoyed explosive growth over the past few decades. As demands for increased capacity and quality grow, improved methods for harnessing the multi-path channel must be developed. The use of adaptive antenna array is one area that shows promise for improving capacity of wireless systems and providing improved safety through position location capacities [1].

Estimating the directions of arrival (DOAs) of electromagnetic waves impinging on antenna arrays is an important issue in array signal processing for wireless communication. It is needed in determining the location of the mobile with high accuracy [2].

Different direction finding techniques and algorithms have been developed leading to significant improvements in DOA estimation over the last decades [3]. Subspacebased methods provide high resolution DOA estimation [4]. However, to date, most of the reported algorithms are based on the uniform linear array (ULA) and the uniform rectangular array (URA) architectures, and very little attention has been given to the circular array topologies despite of their ability to offer a number of advantages. Uniform circular arrays are of particular important in

DOA estimation since they can provide 360º azimuthally coverage and estimate both azimuth and elevation angles simultaneously. In addition, due to its circular symmetry, UCA posses an azimuthally invariant beam pattern, 2D DOA estimation with UCAs is therefore very useful in practical situations, especially in wireless location [5].

In this paper, the problem of estimating the two dimensional DOA using UCA is investigated. This research intends to analyze the performance of UCA using Unitary Transformation MUSIC algorithm in coherent source signals environments.

As the high-resolution MUSIC subspace-based method requires the number of directional sources, its performance is dependent on perfect knowledge of these numbers. This problem is of interest to a wireless location system which necessitates the employment of high resolution DOA estimation method. The performance of AIC, MDL and ET algorithms and their modified versions are discussed.

Fully realizing the potential of these systems requires effective array calibration. Array calibration is necessary to compensate for various non-ideal array effects including amplitude and phase mismatch, mutual coupling effects and error of element locations. In the literature there are generally two kinds of calibration techniques. The first type of method uses signals from known directions transmitted on-site to the antenna array being calibrated and then analyzes the array output. Conceptually, these techniques address each of the above issues [7-8]. The second type of method injects an equal phase signal to all of the channels of the antenna array. While this does address the cabling mismatch issues, it does not address mutual coupling effects, antenna differences, or uncertain sensor locations [9]. A practical calibration approach for UCA is required by real system.

Finally the validation of modified MUSIC algorithm with the measurement data in a wireless location system is presented.

This paper is organized as follows. Section II contains the signal model for antenna array output. Section III describes the basic theory of modified 2D DOA estimation algorithm based on the real-valued unitary transformation MUSIC algorithm for UCA, the estimating the number of coherent sources in colored noise environment and antenna array calibration procedure are also presented in the Section III. Section IV presented the performance analysis and simulation result. Section V contains experimental results illustrating the performance of the described calibration method and Section VI concludes the paper.

• II.    Signal MODEl

Considering a uniform circular array (UCA) consisting of M antenna elements, as shown in Fig.1, the antennas are distributed uniformly over a circle with radius R. The antenna elements operate at a frequency with a corresponding wave length λ. The phase center of each antenna element is located in the xy-plane, at azimuth angle φm=2πm/M with m=1, 2 …M. It is assumed that all antenna elements are identical and omni-directional.

Suppose P narrow band far field signals impinging on the UCA of M elements from directions { θ 1 , φ 1 }, ..., { θ P , φ P }, the received signal at the antenna array can be described as

X ( n )= As ( n )+ n ( n ) (1)

where X ( n )=[x₁( n ), x₂( n ), ... , x_M( n )]^T is the n ^th snapshot of the received signal at the antenna array, T denotes transpose.

A =[ a ( 9 1 , ф 1 ), a ( 9 2 , ф 2 ), ..., a ( 9 p , ф p )], M X P, is a fUllcolumn rank matrix (M>P) of array responses to incident signal from direction { θ 1 , φ 1 }, ..., { θ P , φ P }, and steering vector a ( θ i, φ i )=[ a 1 ( θ i , φ i ), a 2 ( θ i , φ i ), …, a P ( θ i , φ i )] is the array response to the incident signal from direction ( θ i , φ i ), where i=1, 2, …P, and θ i and φ i is the elevation angle and azimuth angle of the i th signal, respectively.

s ( n ) is the incident signal vector and n ( n ) is the n ^th snapshot of the additive noise at the antenna array that is assumed to be a zero stationary complex Gaussian process with variance σ n ², uncorrelated with incident signals.

The covariance matrix of the array response is Rxx=E[x(t)x(t)H]=ARsAH+σn2I , where Rs=E[s(t)sH(t)] is the covariance matrix of the incident signals, I is a MxM identity matrix and H denotes conjugate transpose.

• III.    Basic THeory of modified algorithms

• A.    Basic theroy of modified MUSIC algorithm

To estimation the DOAs of the signal received at the array, the supper-resolution algorithm MUSIC is often used. This algorithm is based on the ensemble-averaged correlation matrix Rx for the antenna outputs. The eigen-decomposition of the covariance matrix R xx is

MH xx i i i i=1

, where e i is the eigenvector of Rx corresponding to the i th largest eigenvalue of Rx and

λ1 > λ2 > … > λP > λP+1 =λP+2 = … =λM =σ2

The MUSIC spectrum is computed by performing an eigenvectors consist of two disjoint subspaces: signal and noise subspaces. The lager and the smaller eigenvalues belong to signal subspace and noise subspaces, respectively. In terms of the orthogonal characteristics of eigenvectors in the signal and noise subspaces, the MUSIC spectrum is typically given by the following:

P ( 9 , Ф ) =

I a ( 9 , ф V |²

Where v and a denote the eigenvectors corresponding to noise subspace and the scanning vector.

If a signal impinging on the UCA at the DOA (θ, φ), set the center of the UCA as reference, then the signal steering vector is a(θ, φ)=[ a1(θ, φ), a2(θ, φ), …, aM(θ, φ)], where am(θ, φ)=exp[j2π(R/λ)sin(θ)cos(2πm/M-φ)],

If the number of antenna elements in a uniform circular array is even, then a m+M/2 ( θ , φ ) M= a m ^*( θ , φ ). And the steering vector a ( θ _, φ ) is easily rearranged in the conjugate centre-symmetric manner, such as a ( θ _, φ )=[ a 1 ( θ , φ ), a 2 ( θ , φ ), …, , a 2+M/2 ( θ , φ ),a 1+M/2 ( θ , φ )]. Then the correlation matrix R xx becomes centre-Hermitian, which is complex-valued.

The real value correlation matrix Ř xx can be obtained by an appropriate unitary transformation Q as

Ř xx =Re{Q^HR xx Q}             (3)

Where if the M is even, the unitary transformation matrix Q for the M-by-M matrix can be chosen as

Q=— (I  jI )             (4)

V211 - jii J

, and I and II are the identity matrix and column flipped identity matrix in the left right direction respectively [6].

The steering vector a’ ( θ _i, φ _i) =Q^H a ( θ _i, φ _i) is a real-value vector, the compute complexity of eigenvalue decomposition and spatial spectrum computation is greatly reduce. In terms of hardware implementation, the implementation of real-valued matrix eigenvalue decomposition is much easier than the complex conjugate symmetric matrix case.

In addition, the backward averaging effect is obtained by selecting only the real part in (3). It is helpful to deal with the DOA estimation of correlated signals [10].

• B.    Estimating the Source Number

Based on subspace decomposition, the space spanned by the eigenvectors of the correlation matrix can be divided into signal subspace and noise subspace. For practical reasons, the covariance matrix and its eigenvalues must be estimated from a finite sample size. The smaller eigenvalues may be different and not equal to σ2, thus it is difficult to determine the number of source by merely observing the eigenvalues.

While the performance of classic MUSIC algorithm depends on the estimation on source number directly, and both overestimation and underestimation will affect the DOA estimation.

Various statistic approaches have been proposed to estimate the number of sources, such as Akaike Information theoretic Criteria (AIC) [11], Minimum Description Length Criteria (MDL) [11] and predicted

Eigen-Threshold approach (ET) [12]. But these approaches couldn’t get a good performance in conditions with colored noise and coherent signal.

To eliminate the inequality of the noise eigenvalues caused by colored noise and coherent signals, the eigenvalues of the R xx are modified as

λ i ^’ = λ i +b i , i =1,2 , …, M.

Where b = У Л , i = 1Д-, M .

ii

У j = 1

Every correction value is related with its former one and itself, so the less the noise eigenvalue is, the greater the correction value is, and the noise eigenvalues become closer to one another. Then MDL, AIC and ET approaches can be used to estimate the source number by solving minimize d

<1 N ( M - d ) log I

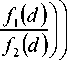
+ f 3 ( d,N ) >

Where

M

f (d )=----ул

1V    L - My 1'

( M Л^{( M} - ^d )

f2 (d )=| Пл I

X i = d +1   )

And the penalty function

I d (2M - d) f (d, N ) = <1 ,        .

3V ’ 12 d (2M - d )log N for AIC for MDL

with N denoting the number of snapshot.

As the MDL and AIC criterion involves extracting the root of M-d, it is difficult to realize real time in FPGA and DSP chips.

The ET method uses a one-step prediction of the threshold for differentiating the smallest eigenvalues from the others and only involves square root.

Let lM - d+1

M

У Л , i=M - d-1

d

then

( d + 1 )

u л M - d

1 + 1 ( N ( d + 1 ))^{- 1} / ² 1 - 1 ( Nd )^{- 1} / ²

l M - d + 1 .

- d

The eigenvalues in the noise subspace should satisfy, ^u

^A M - d — Mm - d

So estimating source number P by finding minimum d which meets Л м - d >  Л М - d .

• C.    Array Calibration Procedure

However, in a real-world, there are some reasons which limit the general use of antenna arrays. One of them is the precise calibration required such arrays when they are used for DOA estimation, which require the acquisition of the precise amplitude and phase relationships of the signal collected at each element. These relations are unfortunately sensitive to many potential error sources, leading to severe performance constraints. An antenna array calibration procedure is a critical stage for utilizing high-resolution DOA estimation algorithms.

Considering the special symmetric structure of UCA, a simple and practical calibration for UCA is presented in this paper. Assume the antenna elements are omnidirection, and a calibration signal transmitter antenna is placed at the center of UCA, the amplitude and phase of received signals Sa( t ) at each element are same in theory.

Assuming no mutual coupling, amplitude and phase mismatch of array elements is taken into account. A distortion matrix G is generally used to encapsulate all of these non-ideal effects, which can be expressed as

C = diag ( a ₁ e^M ,a ₂ e j ^ ² ,...,a_Me^{i < k l} ) .

The received signal at the antenna array can be described as

X(n)=CSa(n)+n(n) , and

R = E (XX H) = CS„SH CH + о 21 = CCH о 2 + о 2NI. aa       NS N

So rn =Ух( n)x1 (n) H = aia1 e^}o2Sa + o„2,i = 1,2 ,l,M i=1

Therefore, the calibration matrix G can be obtained by

G = [g1 ,g2 ,L,gM ], gi = r11 ,i = 1,2,L,M ,

• IV.    simulation result and Performance ANALYSIS

In this section, we investigate the performance of the Uni-tray Transformation MUSIC algorithm through some simulation experiments. An 8-element UCA with the half-wavelength inter-element spacing was considered for the simulation. Antenna elements are labeled as shown in Fig.1, and then the steering vector is conjugated centre-symmetric. So the unitary transformation MUSIC algorithm can be used in a UCA system. Since the estimated correlation matrix is real value, it is simpler to implementation the eigen-decomposition of a real value matrix than that of a complex one.

The simulation will analyze the performance of unitary transformation MUSIC algorithm with comparison with normal MUSCI algorithm ， when there are variation in the Signal to Noise Ratio (SNR) and the resolution of the incoming signal.

A narrowband gauss digital signal s (n T s ) is considered as signal of source, where n=1,2,…N, N is the number of snapshot, T_s is sampling period.

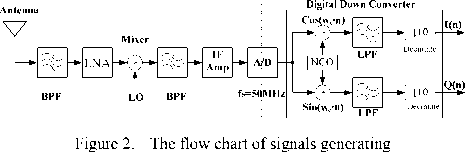
To evaluate the performance of DOA estimation algorithm in hardware systems, the simulated array signals are generated, digitalized and processed as a IF sampling receiver architecture shown in fig.2.

If the signal impinging on the UCA as a plane wave from (0, ф ), the time delay between the element m the center of UCA is T _m= R sin( 9 _t)cos(2nm/M- ф , )/c.

Usually, the delay T _m is less than T_s or not integral multiples of T s , so a signal reconstruction method is considered in modeling array receiving signal

X(t)=[s1(t)+n1(t), s2(t)+n2(t), …, sM(t) +nM(t)], where sm (t )= s (t -

^T m

sinПfst - fTm - k) n(fst - fTm - k) ’

+ГО

) - E s ( k ) k =— to

m = 1,2, l M and nm(t) is the noise on antenna element m which is often assumed that the noise is zero mean and additive.

Colored noise can be generated by passing white noise through a filter with required frequency response.

• A.    Source Number Estimation

Based on the designed UCA, the performances of AIC, MDL and ET are compared with basic algorithm Eigen value, modified algorithm and modified algorithm with unitary transformation correlation matrix respectively.

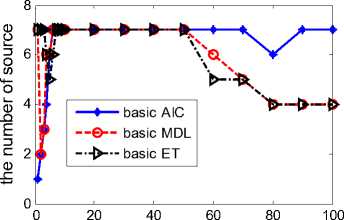
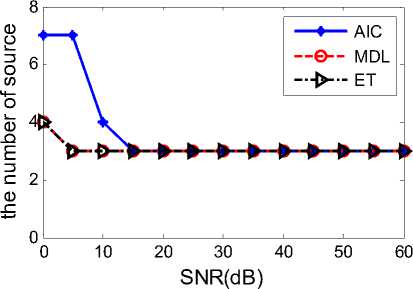
Supposed three uncorrelated narrowband signals impinging on the array from ( 6 1 =10 ° , ф 1 =30 ° ), ( 6 2 =30 ° , Ф 2 =60 ° ) and ( 6 3 =70 ° , ф ₃=120 ° ) respectively. The estimation results of source number are illustrated in fig.3 and fig.4.

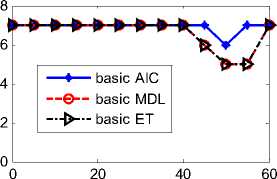
The simulation results show that under a certain condition of some SNR and snapshots, the modified AIC, MDL and ET have good performance in color noise; however, basic AIC, MDL and ET fail in detection under colored noise.

In the coherent sources simulation, three narrowband signals are supposed impinging on the array from (61=10 ° , ф 1 =30 ° ), (62=30 ° , ф 2 =60 ° ) and (63=70 ° , ф 3 =120 ° ) respectively. Signal 3 is the duplication of the signal 2 with delay time t =0.2 ns and signal 1 is uncorrelated with signal 2 and signal 3. The number of snapshot is 100.

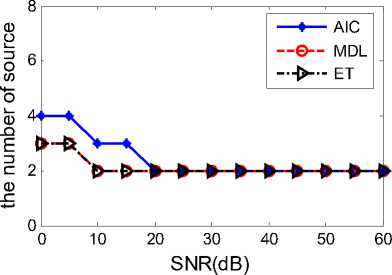
Estimation results of source number with modified eigenvalues algorithm vs. SNR are presented in fig.5 (a). The source number is under estimated. Utilizing the real value correlation matrix obtained by a unitary transformation as (3), the estimation results with modified eigenvalues algorithm vs. SNR are given as fig.5 (b). It shows that the modified AIC, MDL and ET with unitary transformation have good performance in color noise and coherent sources condition.

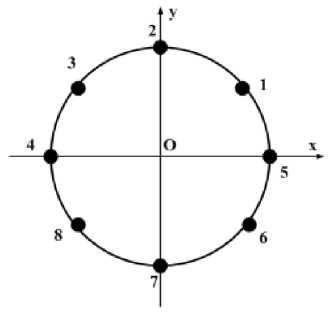
Figure 1. a UCA configuration with conjugate centre-symmetric steering vector

the number of snapshot

(a) Basic algorithms of estimating source number

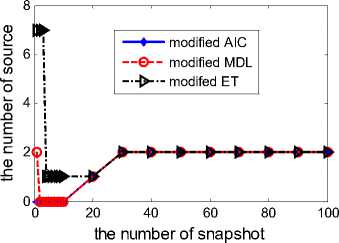
(b) Modified eigenvalue based algorithms

Figure 3. Estimation result of source number with three uncoherent

sources vs. the number of snapshots, SNR=30.

SNR(dB)

(a) Basic algorithms of estimating source number

о сл

о о n E

modified AIC modified MDL modifed ET

20         40

SNR(dB)

(b) Modified eigenvalue based algorithms

Figure 4. Estimation result of source number with three uncoherent sources vs. SNR, the number of snapshots N=100.

1 ° as SNR is more than 10dB. This algorithm shows high resolution capacity in high SNR conditions.

When the number of Snapshot N is 100 and SNR is 30, MUSIC spatial spectrum is given in the Fig.8

(a) Modified eigenvalues without unitary transformation

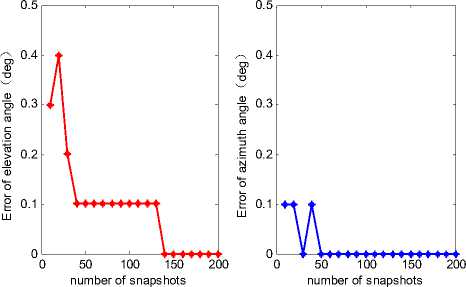
Figure 6.

Absolute error of DOA estimation with one source vs. the number of snapshots , SNR=30dB

(b) modified eigenvalues with unitary transformation correlation matrix

Figure 5. Estimation result of source number with three sources vs. SNR, the number of snapshots N=100, source 2 and source3 is coherent.

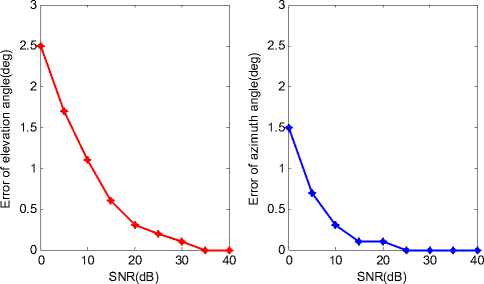
Figure 7. Absolute error of DOA estimation with one source vs. SNR , number of snapshot N=100

• B.    The Number of Snapshot and Signal to Noise Ratio

In this example, we numerically illustrate the Unitary MUSIC algorithm for the case of a single source, assuming the DOA of a desired signal is (6=50 ° , ф =100 ° ). The influences of SNR and the number of snapshots on the performance are investigated.

In wireless location system, some targets usually move quickly, such as in a high speed train and airplane, then the sampling time, i.e. the number of snapshot, is limited. When SNR is 30dB, and the number of snapshots is changed from 10 to 200, the absolute error of estimated result with ideal DOA is given in the Fig.6. It shows that when snapshot number N is more than 50, the error of DOA estimation in short period is small enough to meet the location accuracy.

When the number of Snapshot N is 100, the absolute error of estimated result with ideal DOA vs. SNR is given in the Fig.7. Dynamic range of the MUSIC spectrum can be improved by increasing the SNR, and it provides better estimation performance. Moreover, the estimation errors of elevation and azimuth angles are both less than

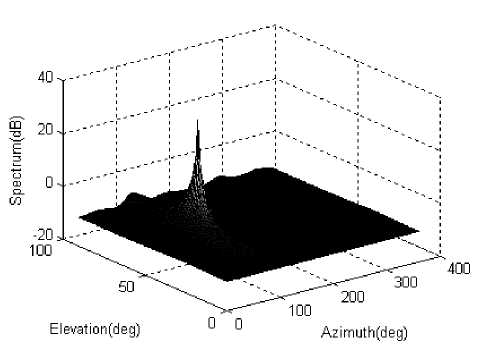
Figure 8. Spatial spectrum of the Unitary MUSIC algorithm, one signal from (50°, 120° ), SNR=30dB, number of snapshot N= 100

• C.    Uncorrelated Signals and Coherent Signals

The two directional signals are said to be fully correlated or coherent when one is the delay and scaled version of the other. Multipath signals normally result in partial correlation. Correlation between two directional signals limits the applicability of basic MUSIC algorithm, whereas the real-value unitary MUSIC algorithm can deal with two correlated signals.

For example, two correlated narrowband signals impinging on the antenna array from (6 1 =10 ° , ф 1 =30 ° ) and (6 2 =30 ° , ф ₂=60 ° ) respectively, and signal 2 is the duplication of the signal 1 with delay time T =0.3ns.

If SNR is 40dB and snapshot N is100, there is only one peak in the spatial spectrum of basic MUSIC algorithm, as shown in Fig.9. The estimated number of source is 1, and the estimated DOAs (6 1 =19.1 ° , ф 1 =52.6 ° ) are incorrect.

Even if the number of source is given as 2, the spatial spectrum of basic MUSIC algorithm is given in Fig.10. the estimated DOAs are still incorrect.

While, the spatial spectrum of unitary transformation MUSIC algorithms is presented in Fig.10. There are two sharp peaks in the spatial spectrum. The estimated DOA is identical to the ideal DOA. It shows that unitary MUSIC algorithms can correctly estimated DOA of two correlated signals.

The results of DOA estimation error vs. SNR are also presented in the Fig.11, it shows that the DOA estimation resolution depends on SNR, and adequate SNR levels are necessary to get high accuracy.

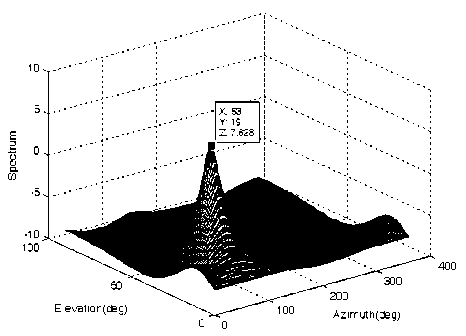
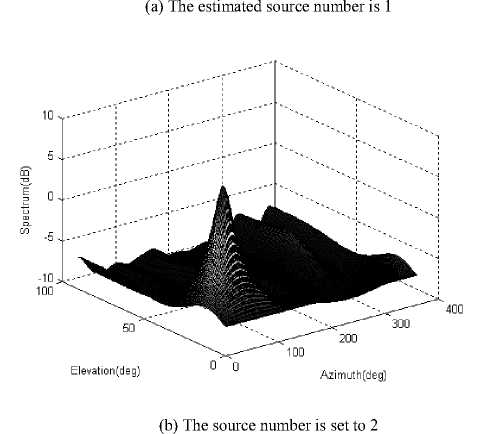
Figure 9. Spatial spectrum of basic MUSIC algorithm, two correlated signals with arrival angle of (10 ° , 30 ° ) and (30 ° , 60 ° )

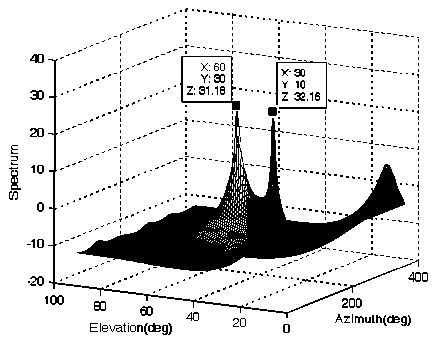
Figure 10. Spatial spectrum of unitary transformation MUSIC algorithm, two correlated signals arrival angle of (10 ° , 30 ° ) and (30 ° , 60 ° )

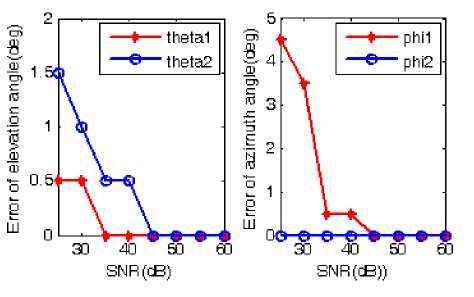
Figure 11. Absolute error of DOA estimation with two correlated source vs. SNR, Snapshot N=100

• V.    experiment Result and Discussion

The performance of 2D DOA estimation based on the unitary MUSIC algorithm for UCA is validated in a wireless location system, which operates at VHF band. The design and implementation of the necessary hardware to prove the feasibility of high resolution DOA estimation was achieved.

An 8-Monopole element UCA and an 8-channel heterodyne array receiver are implemented, and the signal processing subsystem is FPGA and DSP based. The computation flow of the unitary MUSIC DOA estimation algorithm involves 3 main steps: (1) estimation of the sampling real value correlation matrix with unitary transformation; (2) eigenvalue decomposition (EVD) of the correlation matrix; (3) estimate the number of source based on the modified eigenvalues algorithm; (4) the computation of MUSIC spectrum and search peaks in the 2-dimension spatial spectrum. The first step is implemented in a FPGA chip, and then the EVD computation, the number source estimation and peak search process are processed in a DSP chip.

The DOA estimation performance for one source is tested in a open area with the wireless location system. The ideal DOA of the source is (6 1 =157.15 ° , ф 1 =76.99 ° ). The estimated DOA in DSP with 200 snapshot is (61=158 ° , ф 1 =76.5 ° ). Fig.12 is the spatial spectrum based on the estimated correlation matrix calculated in the FPGA.

The measured data validate the performance of Unitary Transformation MUSIC algorithm, while the DOA accuracy and resolution is highly depended on the environments and channel calibration. A calibration approach that significantly improves the performance of the estimates is undergoing.

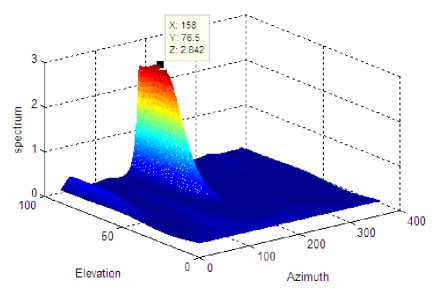
Figure 12. Spatial spectrum of unitary MUSIC algorithm based on measured data with 20 snapshot, one source from ( 6=157.15 ° , ф =76.99 ° ).

• VI.    Conclusion

This paper has deal with some facets of two dimension DOA estimation in UCA. This paper has introduced the 2D unitary transformation MUSIC algorithm in UCA. And modified eigenvalues based algorithm to estimate signal number is present and analysis.

In this paper, we have shown the influence of colored noise and coherent sources, SNR and snapshot number on the 2D DOA estimation of UCA by means of simulations; we also verified the results by measurements data.

It turns out that,

Therefore, detail investigation to verify the performance by simulation which takes into account mutual couple and other error and by means of measurements are still in progress.

This work was supported in part by fund of National Key technology R&D program (2008BAC36B02 ) and National Natural Science Foundation of China ( 10975056 )

• [1]    A. Pages-Zzamora, J. Vidal, “Evaluation of the improvement in the position estimate accuracy of UMTS mobiles with hybrid position techniques”, in IEEE VTC 2002 ， vol.4, pp, 1631 － 1635, 2002

• [2]    Nikos Deligiannis, Spiros Louvros, “Hybrid TOA-AOA location techniques in GSM Network”, Wireless Pers Commun. 2010, Vol.54, pages:321-348

• [3]    H.KRIM and M. VIBERG, “Two decades of array signal processing research : the parametric approach”, IEEE Signal processing Mag., vol.13, no.4, pp.67-94, 1996

• [4]    R.O. Schimidt, Multiple emitter location and signal parameter estimation, IEEE Trans. Antenna Propagation, vol. 34, No.3: 276-280, March 1986

• [5]    Yufeng Zhang, Zhongfu Ye, Chao Liu, “An efficient DOA estimation method in multipath environment”, Signal Processing 90 (2010): 707-713

• [6]    Kim, M. (2004), "Hardware implementation of signal processing in smart antenna systems for high speed wireless communication", Department of Electrical and Computer Engineering, Yokohama National University, Yokohama, PhD thesis.

• [7]    Kapil R. Dandekar, Hao Ling and Guanghan Xu, “Smart antenna array calibration procedure including amplitude and phase mismatch and mutual coupling effects”, 2000 IEEE International Conference on Personal wireless communications, 2000, Dec. 17-20, pp. 293-295

• [8]    Y. Chen, A. Chang, and H. Lee, “Array Calibration Methods for Sensor Position and Pointing Errors,” Microwave and Optical Technology Letters , vol. 26, pp. 132-137, 2000.

• [9]    R. Ertel, Z. Hu, and J. Reed, “Antenna Array Hardware Amplitude and Phase Compensation Using Baseband Antenna Array  Outputs,”  1999 IEEE Vehicular

  Technology Conference Proceedings, vol. 3, pp. 17591763, 1999.

• [10]    K. Huarng and C. Yeh, “A unitary transformation method for angles of arrival estimation”, IEEE Tran. Acoustic, Speech, Signal Processing, vol. 39. No.4. pp.975-977, April. 1991.

• [11]    M. Wax, T. Kailath. Detection of signals by information theoretic criteria. IEEE Trans. on Acoustics, Speech and Signal Processing ,1985, 33(2): 387–392.

• [12]    W. G. Chen, K. M. Wong, J. P. Reilly. Detection of the number of signals: a predicted eigen-threshold approach. IEEE Trans.on Signal Processing , 1991, 39(5): 1088–1098.

Ping TAN received the B.S and Ph.D degrees in electrical engineering from Huazhong University of Science and Technology, wuhan, China, in 1996 and 2004, respectively, and the M.S. degree in radio physics from Chinese Academy of Sciences in 2000.

She is currently a lecturer with the department of Electronics and Information Engineering, Huazhong University of Science and Technology, and Wuhan National Laboratory for Optoelectronics, Wuhan, China. Her areas of research include array signal processing, wireless location and computational electromagnetics.