Study of hydrodynamics features in the apparatuses with movable nozzle

Introduction. The defining feature of heat and mass transfer processes, which occurs in the three-phase flows, is the interaction phase, which determines the value of the interfacial surface. Therefore, apparatuses for the heat and mass transfer processes must be designed so that they have a maximum contact surface. Classification of heatmass exchange apparatuses (HMEA) provides geometric features of the apparatus and the hydrodynamic condition they create. However, the main trend which remains dominant in the design of such apparatus is to create a thin film of liquid on the surface of the nozzle.

Apparatuses with a movable nozzle (AMN) were developed in relation to the implementation process of dedusting and degassing and absorption in a number of countries: Canada, the USA, Germany, Japan, CIScountries [1; 2]. AMN advantages over other types of contact devices, which determined their widespread occurrence: steady operation in the polluted environments of self-cleaning nozzle surfaces and walls of casing, low sensitivity of the device characteristics to sudden load fluctuations of gas and liquid; indiscriminateness to the initial liquid distribution, which is important for industrial AMN; high lateral uniformity simplifying scalability; a wide range of workload (in [3–7] a value q l up to 200 m³/(m² ⋅ h is reported) and w g up to 8 m/s at an empty AMN intersection); high intensity of exchange processes in the layer; constructive design simplicity; compactness; low weight and cost of the nozzle.

So far published information about the interaction of the three phases in the HMEA varies by the difference in the representation quality and experimental data discrepancies in all major aspects of the movable layers behaviour, so that its practical use in the engineering calculations is complicated. The study of the quite complex

“gas–liquid–solid” system behaviour remains largely experimental. Prospects of AMN use for evaporative water cooling require special consideration. AMN is advisable to apply for the organization of such mass transfer processes in which the main resistance of mass transfer is focused in the gas phase, typical for the process of evaporation cooling in the cooling towers [4].

Therefore, the work was aimed at choosing the solution in which the MN of the HMEA can be used to implement the contact handling process of gases and liquids with density values clarification of the nozzle elements (p ne ) and the column dynamic height ( Н dh ) and obtain the specified calculated dependences which describe the hydrodynamics and mass transfer in AMN, that is to create bases for engineering calculations [8–12].

Studying of evaporative water cooling processes was carried. Studying of evaporative water cooling processes was carried on a laboratory model using different nozzle elements (see table).

From a scientific and practical point of view, the issue concerning the nature of the transit of nozzle layer from a stationary to a moving condition seems important. The issue is complex and poorly studied. Typical modes of movable nozzles (MN) behaviour in the apparatuses are shown in fig. 1.

Fixed layer porosity does not depend on the load of the gas and the liquid. Traditionally, the critical transition velocity ( w _0, w ₀ ' ) is determined by visual pseudofluidization curve analysis that is described by the dependence Δ р = ( w g , q l ). We conducted its specification by constructing selective Lа ( w g , q l ) under the following conditions: H dh = 0,1 m, d ne = 0,04 m, p = 300 kg/m³, q l = 15 m³/(m²h) (fig. 2).

Studied nozzle elements characteristics

№	NE type	Nozzle material	Geometry dne , mm	ρ ne , kg/m3	Note
1	d ne	Foamed polypropylene	40.1	248	Commercialization of elements
2			40.3	305
3			36.6	335
4			35.6	367
5	d ne	Empty celluloid ball which is partly filled with water	37.1	100–1000 in increments of 100 units	Size ρ ne for the empty element 91 kg/m3

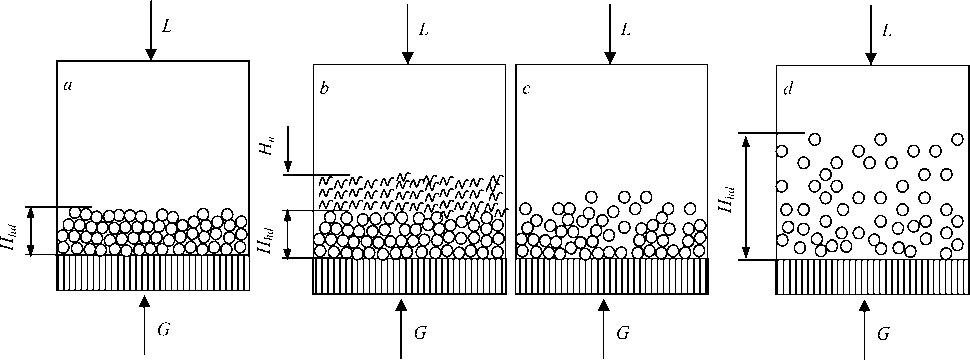
Fig. 1. Typical AMN modes: a – stationary; b – stationary nozzle flooding; c – initial pseudo-fluidization; d – developed pseudo-fluidization

Рис. 1. Характерные режимы АПН: а – стационарный; б – захлебывание стационарной насадки; в – начальное псевдоожижение; г – развитое псевдоожижение

Speed w g is given to the empty column crossing; fixed (1, a ) and initially compacted layer of nozzle elements (1, b ) having the ability to expand is considered. Value w g ^*: w отр – the maximum speed at which the curves coincide Δ p for fixed and movable layers; w з – the beginning of stationary nozzle flooding; w _o, w _o ' – the beginning of pseudo-fluidization; w ₁ – the beginning of active pseudofluidization; w_i – inversion beginning. Let us specify some definitions through the variety of existing formulations for w g^* : w з corresponds to the intensive growth Δ p , layer turbidity, foam formation atop of the layer (partially inverted cocurrent). For the fixed layer speed w з is unchanged for specific loadings; for an extending layer w з depends on the porosity and cannot be described by the known dependencies; w o is the minimum gas velocity at which steady vertical oscillations of several adjacent NE are observed ; w ₁ corresponds to the active movement and mixing of NE; w_i is the beginning of NE inversion – their concentration near restrictive gates. The latter mode is almost immediately transformed into “upper” NE flooding, which is typical for the fixed layer (fig. 1, b ).

Value w o ' is clearly recorded on vibrocurve L a ( w g ) as a leap ( ≅ 20 dB or 30 % ) and mild stated on fluidization curve (column walls vibroacceleration is defined by the movable nozzles state). Almost constant vibroacceleration level ( L_a = 5.5 w_g ^0,08 ) corresponds to the stationary layer state. The NE transition to movable state was much more difficult, as compared to the traditional presentation. If w g ≅ w o ' then the described unstable pseudo-stationary NE states are formed during periodic movement of an individual NE (layer alteration with changing porosity) at a constant load. Their duration ranges from tens of seconds to several minutes. The layer structure is changing and fluid retention therein varies, i. e. the w o ' value is characterized by a certain range of existence. The width of this range depends on the initial layer density which is determined by NE own weight and the action of external loads and vibrations. For example, for NE with ρ ne = 300 kg/m³ and d ne = 0,037 m, this value is 0.4 m/s.

We found that the elements with ρ ne < 200 kg/m³ transferred to a moving state, bypassing flooding in a stationary state, for ρ ne > 200 kg/m³ pseudo-fluidization is carried out in pseudo-stationary flooding condition of the extending layer; for ρ ne > 700 kg/m³ this pattern persists for larger values of H_p , and the part of liquid is taken outside of the layer and placed on top of its upper limit as the layer of foam with thickness H_n over 0.02 meters.

Gas and liquid layer load effecting movable nozzles retaining ability Н dh = 0.1 m is shown in fig. 3.

The best range to implement mass transfer processes seems to be that of ρ ne ІІ (ρ ne = 200–700 kg/m³). Partial fixed layer flooding precedes the beginning of pseudofluidization; the nature of the transition determines the entire future behaviour of the system. The speed of the apparatus starting to flood w 3 is quite high (≈ 6 m/s); liquid withdrawal Δ G_l from the working area is slow until the speed value is w 3. This range differs by a wide work area of speed w g , acceptable values of fluid withdrawal Δ G_l and a relatively small dynamic height of the layer H_l .

Regarding this area let us consider the characteristic pseudo-fluidization modes:

• 1.    0 < w g ≤ 2.0 m/s – Stationary system state with characteristic local restructuring of fixed layer structure and some porosity growth. Linear growth H l ( w g ) until the beginning of the pseudo-fluidization speed w 0 ' with the progressive flooding of the fixed reconstructed layer.

• 2.    2.0 < w g ≤ 2.5 m/s – Initial pseudo-fluidization mode (transitional mode). There is a characteristic peak H p by the speed of gas w 0 ' (fig. 3, a ) with the consequent restoration to the previous value; the system is unstable, the part of the layer remains stationary and its periodic restructuring occurs. Fluid retention for q_l < 5 m³/ (m² ⋅ h) (fig. 3, b ) in active pseudo-fluidization mode decreases to values which are characteristic of the stationary layer. This is a border q_l ^∗ for cooling towers with movable nozzle (CTMN) related to layer drainage; here CTMN operation is not feasible, despite the liquid being in the layer for a long time.

• 3.    2.5 < w g ≤ 6.0 m/s – Developed pseudo-fluidization mode. The entire nozzle layer is movable, the system is homogeneous. Comparison of system characteristics with the similar mode for the zone ρ ne І shows that the new transition patterns to mobility impacted the behaviour of the system as a whole: the initial flooding state is supported. However, it does not further develop with the increase of w_g to the developed flooding due to a mechanism that compensates the layer expansion. This kind of situation when the initial flooding supported in a wide range of w g , provides the possibility of stable AMN operation in the high loads mode. Within the described mode, we can distinguish the area w g ≅ 4.7–6.0 m/s, where there is no dependence of H l on w g . This new area precedes a sharp increase of H l .

• 4.    6.0 < w g ≤ 8.0 m/s. In fact, that is the previous mode with a sharp increase of flooding component. Con-

• ventionally, it can be called a movable layer flooding mode, noting a significant difference from the same mode with a stationary nozzle. Whereas, under the latter conditions, the flooding mode means the practical impossibility of further employment, but concerning the apparatuses with a movable nozzle this possibility remains, due to the liquid capacity of the apparatus and very high intensity of the process.

Processing of experimental information. The most important hydrodynamic characteristics of cooling towers with movable nozzle (CTMN), which are required for engineering calculations, are critical speeds ( w 0 ' , w 1 ), pressure loss in the working area ( Δ p ), fluid retention ( H l ) and dynamic layer height ( H Д ). This information allows selecting the operating mode of heat-mass exchange apparatus (HMEA), calculating the height of the columns and fan power [13–15].

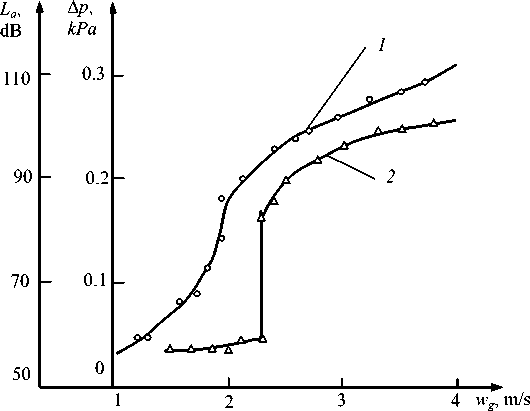
Fig. 2. Experimental dependences: 1 – pseudo-fluidization curve Δ р = f ( w g ); 2 – vibrocurve L a = f ( w g )

Рис. 2. Экспериментальные зависимости: 1 – кривая псевдоожижения Δ р = f ( w_g ); 2 – виброкривая L_a = f ( w_g )

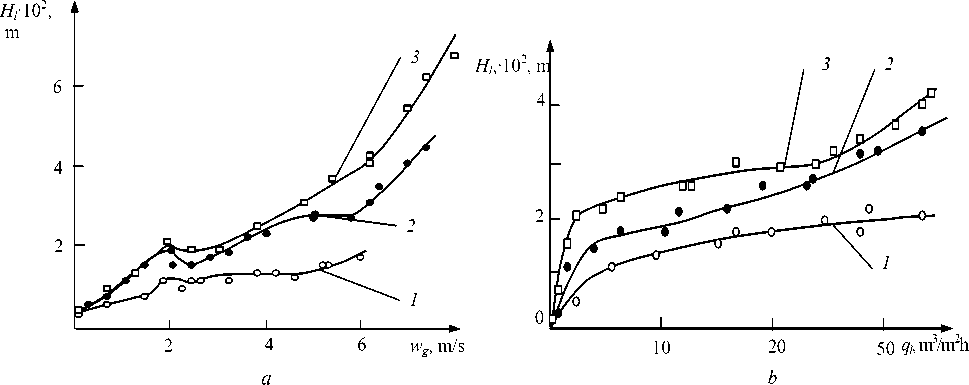
Fig. 3. Dependence of retaining ability of the movable nozzle on gas and liquid loads at Н_dh = 0.1 m:

1 – ρ ne = 100 kg/m³, 2 – ρ ne = 500 kg/m³; 3 – ρ ne = 800 kg/m³; a – H l = F ( w g ); b – H l = f ( q g )

Рис. 3. Зависимость удерживающей способности слоя подвижной насадки от нагрузок по газу и жидкости при Н dh = 0,1 м: 1 – ρ ne = 100 кг/м³; 2 – ρ ne = 500 кг/м³; 3 – ρ ne = 800 кг/м³; а – Н l = f ( w g ); б – Н l = f ( q g )

For non-irrigated layers the equation is obtained:

Re0      dn v g

Ar g

1301 - 3 ^ 0- + S o

where, in order to record the peculiarities of the compressed flow of balls with gas stream the stationary layer porosity is used. Equation (1) provides the calculation w o for the layer of balls with diameter of the nozzle elements d ne = 35...42 mm and density ρ en = 90...1000 kg/m³ for H ст > d ne . Nozzle irrigation leads to a decrease of w ^* _g ( w o ^' ), and with the increase of ρ ne the w o ^' value decreases. With regard to the influence of q l and p не let us write down:

4320 -p - }²¹ -to o

4320p-}21 + qlI-1’25'10-4pne +0,275).

This equation is fair for 200 <  p _ne <  1000 kg/m³ and 5 <  q l <  25 m³/(m²^h). For p _ne <200 kg/m³ dependence of w 0 ' = F (ρ ne ) appears to be bigger. The w 1 value characterizes the transition to the developed pseudo-fluidization, i. e. to the uniformly pseudo-fluidized layer:

Ю 1 = 1,4 - © 0 -

The width of the area of initial pseudo-fluidization sharply increases with ρ _ne growth and the layers of nozzle elements (NE) with density ρ _ne > 500 kg/m³ operate in practice only in this mode.

Dynamic height is characterized by a mean value of oscillating movable nozzle (MN) level, and was determined visually. In the stationary state, these oscillations are characterized by constant amplitude:

Нd = Нhd + Нhd (tog "®0)X

X [ 16,2 exp ( - 0,002 p _ne - 70 d_ne ) + 0,007 q l ] .     (4)

If w g = w o ^' , then value Н d = Н dh . This formula provides a calculation of Н_d for dry layer of MN, as well; it is fair in the range of w_g = w _o - 4.5 m/s; q l <  25 m³ /(m²^h); Н dh = 0.5–0.2 m; ρ ne = 90–1000 kg/m³, d ne = 0,035–0,042 m.

The gas stream pressure loss value Δ p determines the capacity of the electric fan motor (excluding energy consumption for separation and loss in communication).

[ Ар |

Traditionally the ratio I —— I is used, but the main MN l Н hd )

layer characteristic is its dynamic height Н dh . Complex

I Ар ।

leads to a distortion of the physical scene, as, l Н hd )

for example, with ρ ne = 1000 kg/m³ this value exceeds 10⁴ Pa/m. This maximum value corresponds to the weight of the fixed layer NE, where voids are completely filled with liquid. This should result in the inverted cocurrent if losses are greater than 10 Pa/m, which in practice is not observed even at w_g > 8 m/s. So it is worthy using

,           . „ ,        ■                ,                             I Ар

the specific dynamic pressure loss, i. e. the value l Н d

.

I gM i

It consists of a dynamic specific NE weight ne and FH кd pressure loss Δpd, that characterize the contribution to the general value of the detained fluid pressure loss and friction due to the elements mixing in the pseudo-fluidized layer:

gMne

^А р = ^А p d H d ⁺ —p—, F_k

А р d = 0,8 Н hd ⁰’⁶⁵to g x                 (5)

x ехр(1,85 -10-3 pne +1,56 -10-2 ql + 2,86), where Мne – NE layer mass.

The equation is adequate to the experimental data with an average relative error 0.11 and is fair in the ranges: 0.05 <   H_dh <  0.2 m; w _o<  w_g <  4.5 m/s;

• 5    <  q l <  25 m³/ (m² - h); 200 <  p _ne <  1000 kg/m³.

Increase of H_dh leads to the decrease of А р_d , which indicates pseudo-fluidization quality deterioration. For the elements with p _ne = 90 kg/m³ the А р_d value does not depend on w_g ; for w_g = w _o the smallest difference of А р_d occurs, which was obtained for different densities ρ ne . Heavier NE correspond to the greater value А р_d , which match physical presentations. For q l < 5 m³/(m² - h) the exponential nature of equation (5) is disturbed.

Conclusion. The apparatuses with a movable nozzle are a promising solution of column HMEA, which enables operation in the extreme conditions (contaminated environment, sharp fluctuations of loads), increased limit loads, high lateral uniformity of fluid (scaling task simplification), and lack of demands to the flow distribution quality. The best ranger for mass transfer processes implementation is that of ρ ne ІІ (ρ en = 200–700 kg/m³), which is distinguished by a wide working area according to w g , acceptable values of fluid withdrawal and a relatively small dynamic layer height.

Necessary dependencies for engineering calculation were obtained, which determine the critical speed value ( w 0 ' ), the pressure loss in the working area (Δ р ) and the dynamic NE layer height ( Н д ).

It remains necessary to study the dynamics of gasdroplet flows in the system to provide for calculation of fluid distribution units, drop moisture separation, environmental emission and scattering therein, to consider the issues of the applied nature (scale factor, work in long-term inclines and tossing; the accumulation of impurities in the recirculation liquid, etc. An improved constructive design of devices with the movable nozzle shall be developed.