Study of Multi-Level Cryptography Algorithm: Multi-Prime RSA and DES

The primary objective of this study is to understand and implement multi-level encryption using RSA and DES. A sample plaintext data is encrypted using a combined approach of the two algorithms. Decryption is performed accordingly and the time and memory parameters are noted. The RSA algorithm has been one of the most popular asymmetric algorithms for public key cryptography.

The strength of the RSA algorithm has been the difficulty of extracting two large prime numbers from their product, i.e., factorization of the large number obtained from their multiplication [1].

This strength was further utilized by implementation of the multi prime RSA algorithm, wherein, more than 2 prime numbers are used to generate the private and public key [2]. This implementation leads to a substantial increase in decryption time with increase in the number of primes.

Since RSA is an old algorithm, using it to transfer large amounts of sensitive or confidential data is not pragmatic. Hence, the DES algorithm is used to encrypt the raw data. Another layer of encryption is added on the DES key using the RSA algorithm [4]. This solves the problem of DES symmetric key secure sharing. This can be shown this form of a block diagram in figure 1 [5].

“DES: (Data Encryption Standard), was the first encryption standard to be recommended by NIST (National Institute of Standards and Technology).” DES has a key size of 64 bits and block size, also 64 bits. Many attacks and analysis have explored the weaknesses of DES, which make it somehow a vulnerable form of block cipher [6] [7].

Plaintext

DES Encryption

DES Key

RSA Encryption

Cipher-text

Channel / Medium

Cipher-text

RSA Decryption

DES Decryption

DES Key

Fig.1. Multi-Level RSA and DES Block Diagram.

Plaintext

Triple DES is a stronger variant of DES. It also has a 64-bit block size along with 192 bits of the key size. The encryption process in Triple DES is same as that of DES, but the whole set of steps is applied three times for more security. A combination of different keys are used for implementing Triple DES [6].

In this paper, we will implement a combination of the standard RSA and DES algorithm, and then substitute RSA with its variant, the multi-prime RSA. The rest of the paper includes the following; a brief Literature Review of this algorithm and its variations is given in section II. Section III is about the standard working of RSA Algorithm with DES. Section IV discusses the methodology used in implementing n-prime RSA with DES with comparisons of encryption and decryption times with standard RSA. It also includes memory consumption averages as another comparison parameter. Section V discusses results and graphical representations of the data collected. Sections VI and VII discuss the future scope and limitations of our research, respectively, and Section VIII concludes the paper.

• II.    Related Work and Implementations

The idea if combining RSA and DES to reap the benefits of both symmetric and asymmetric key encryption is not a new one. Security, being a prime issue has always been researched and experimented extensively. Below are some recent related work and implementations that use the Hybrid Cryptography approach.

A framework for data security was proposed in 2016, where separate frames were designed for client and server. A user registration process was included on the server side for authorization. The approach included 3 phases to be applied on the data, namely, DES, RSA, Hybrid algorithm. The keys that were used in the last step were string, modulus, private, public and integer key [8].

Another approach was proposed for combining symmetric and public key methods in 2012. Again, AES and DES were used for data encryption and RSA was used for key exchange. The system comprising of many modules was modelled using Verilog HDL using Mdel Sim SE 5.7e. It also consisted of a pseudorandom number generation unit for the key generation process in addition to a GCD computation unit to be used in the RSA algorithm [9].

Aiming ay user’s integrity, authentication and accuracy, this approach uses two different cryptographic algorithms for both encryption and decryption. A public key cryptographic algorithm based on linear block cipher and other is based on symmetric cryptography algorithm [10].

Multilevel and hybrid cryptography algorithms are used to enhance the security of cloud database, for Database-as-a-service . The cryptography tools used are RSA, DES and Random Number Generator. This technique is more profound on small amount of data like passwords [11].

Hybrid algorithm based on RSA and DES is put forward to increase the Data Transmission security in Bluetooth communications. Instead of the current encryption method in Bluetooth, that is, E0 encryption, which is 128-bit symmetric stream cipher, DES and RSA are used. DES being a block encryption, provides higher data transmission efficiency and RSA encrypts the DES keys. This combination makes the Bluetooth Transmission more reliable and secure than E0 encryption [12].

• III.    Multi-level Cryptography

Multi-level cryptography was implemented using DES and RSA, and subsequently using DES and Multi-prime RSA.

The steps followed for the same are illustrated in the following flow charts [4] [13]:

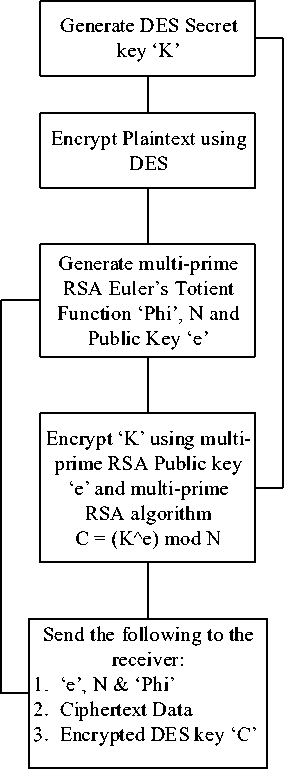
Fig.2. Multi-Level Encryption on Sender Side.

• A.    Encryption

At the sender side, encryption is done as follows [4] [13]:

• •    Generate DES Secret key. (Since DES is a symmetric key algorithm, only one key is generated and shared).

• •    Use this Secret Key to encrypt the plaintext data using DES.

• •    Generate RSA Public Key ‘e’.

• •    Use this key to encrypt the DES Secret Key using the RSA algorithm.

• •    The following information is shared with the receiver.

• 1.    RSA Public Key ‘e’ and (Euler’s Totient function), product of primes N.

• 2.    Encrypted Data

• 3.    Encrypted DES Secret key

• B.    Decryption

At the receiver side, Decryption is done as follows:

• •    Generate the private key, ‘d’ using Φ and ‘e’.

• •    Use this key to decrypt the DES secret key using RSA.

• •    The secret key thus obtained is then used to decrypt the cipher-text data using DES.

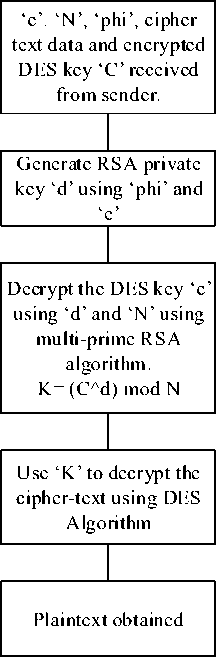
Fig.3. Multi-level Decryption on Receiver Side.

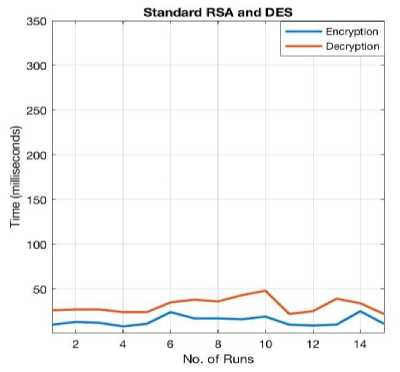
Fig.4. Encryption/Decryption Times for Standard RSA+DES

• IV.    Methodology

The problem of key sharing in the DES arises due to the symmetric nature of the algorithm. By using an asymmetric algorithm to encrypt the shared DES key, this concern can be eliminated [14]. Further, the approach here is to see how practical and feasible it is to apply the multi prime version of RSA in combination with DES.

The following sections cover implementation and the average encryption and decryption times of 3-prime, 4-prime and 5-prime RSA with DES, and the average memory consumption of DES+RSA with 2-10 prime numbers used.

We have used bit length of 1024 and 256 bytes is the block size, the time has been recorded in milliseconds (ms).

• A.    DES and 3-Prime RSA

The 3-prime RSA encryption is used in place of the standard RSA. The DES algorithm remains the same. Hence, the DES key is encrypted using 3-prime RSA.

This implementation does two things, one, it encrypts the DES secret key using RSA, and two, it encrypts the main data to be transmitted using DES.

Hence, at the receiver side, decryption also needs to be done at two levels. The first step is to decrypt the RSA encrypted DES key, and the second is to decrypt the actual data using the key obtained in the first step.

It is important to note here that RSA in isolation is not a strong encryption strategy whereas DES is. Combining the two might not necessarily increase the strength of the security of the data, but definitely makes it more difficult and time consuming for any potential attacker. This technique combined with other detecting mechanisms can help in the identification of an attack before it actually escalates to a dangerous level.

Following results were obtained when DES and Standard RSA was implemented in JAVA:

Average running time for encryption: 14.133333 ms

Average running time for decryption: 31.333333 ms

Average Memory consumption: 24.08738556 MB

Average running time for encryption: 18.1 ms

Average running time for decryption: 77.8 ms

Average memory consumption: 27.12103221 MB

Encryption Decryption

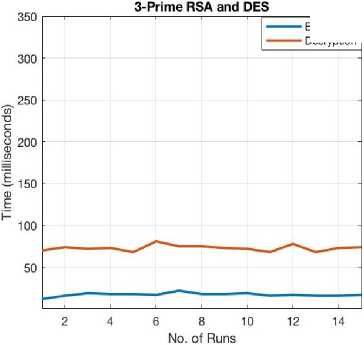
Fig.5. Encryption/Decryption Times for 3-prime RSA+DES.

• B.    DES and 4-Prime RSA

The 4-prime RSA encryption is used in place of the standard RSA. DES encryption/decryption remains the same.

• D.    DES and 6-Prime RSA

The 6-prime RSA encryption is used in place of the Standard RSA. The DES encryption/decryption remains the same.

Average running time for encryption: 18.9 ms

Average running time for decryption: 163.7 ms

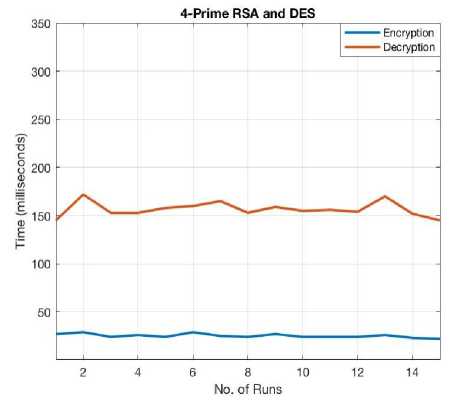
Fig.6. Encryption/Decryption Times for 4-prime RSA+DES.

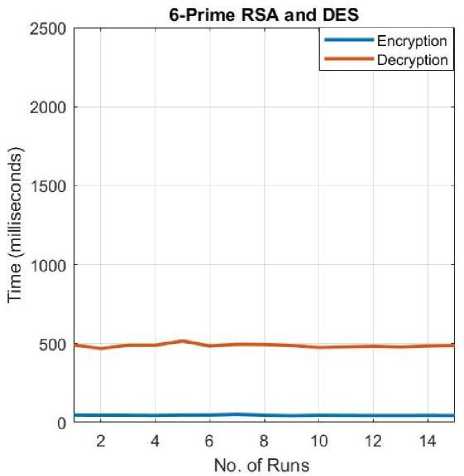
Fig.8. Encryption/Decryption Times for 6-prime RSA+DES.

C. DES and 5-Prime RSA

The 5-prime RSA encryption is used in place of the standard RSA. DES encryption/decryption remains the same.

Average running time for encryption: 24.7 ms

Average running time for decryption: 312.9 ms

Average memory consumption: 15.43968793 MB

5-Prime RSA and DES

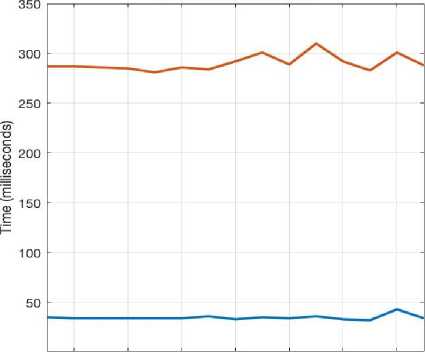
2       4       6       8      10      12      14

No. of Runs

Fig.7. Encryption/Decryption Times for 5-prime RSA+DES.

After 5 prime numbers, to proceed further, we reset the Y- axis upper limit to a much higher value for the purpose of clarity in comparison.

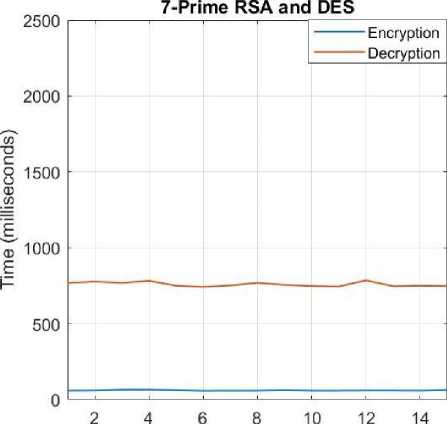
• E.    DES and 7-Prime RSA

The 7-prime RSA encryption is used in place of the Standard RSA. The DES encryption/decryption remains the same.

No. of Runs

Fig.9. Encryption/Decryption Times for 7-prime RSA+DES.

• F.    DES and 8-prime RSA

The 8-prime RSA encryption is used in place of the Standard RSA. The DES encryption/decryption remains the same.

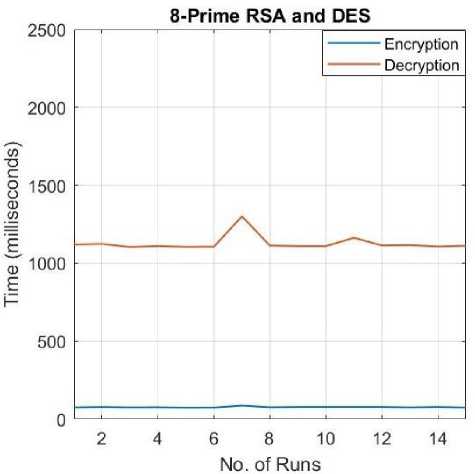
Fig.10. Encryption/Decryption Times for 8-prime RSA+DES.

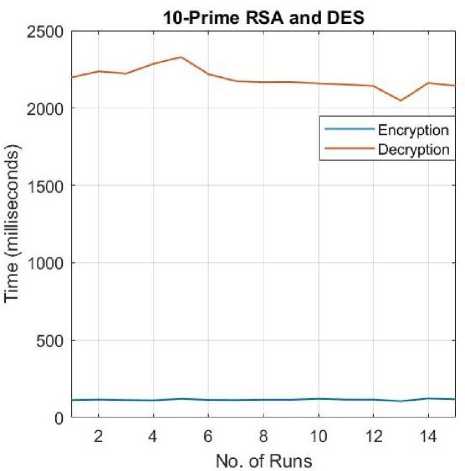
Fig.12. Encryption/Decryption Times for 10-prime RSA+DES.

• G.    DES and 9-Prime RSA

The 9-prime RSA encryption is used in place of the Standard RSA. The DES encryption/decryption remains the same.

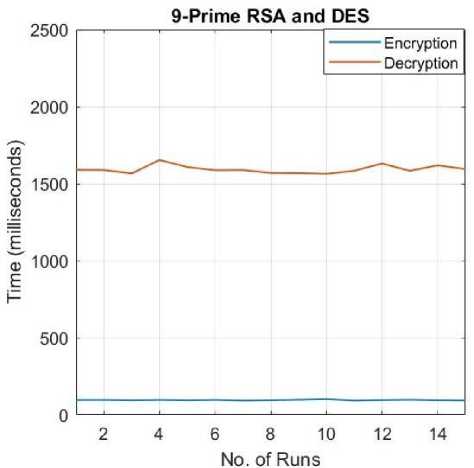
Fig.11. Encryption/Decryption Times for 9-prime RSA+DES.

• H.    DES and 10-Prime RSA

The 10-prime RSA encryption is used in place of the Standard RSA. The DES encryption/decryption remains the same.

• V.    Results

Following is the tabular representation of the average encryption and decryption time values for the various versions of RSA algorithm that have been used to encrypt the DES key. The table also shows the average memory consumed by each of these programs.

Table 1. Average Encryption / Decryption Time Values, and Memory Consumption of Combined Multi-Prime RSA and DES.

No. of primes used in RSA	Average Encryption Time (ms)	Average Decryption Time (ms)	Average memory used. (MB)
2	14.133333	31.333333	24.08738556
3	17.266666	72.933333	27.12103221
4	25.2	156.666666	7.463562012
5	34.733333	290.133333	15.43968793
6	46.733333	487.266666	23.91811218
7	60.6	759.466666	30.69079132
8	76.866666	1127.666666	6.035212708
9	96.133333	1592.4	13.80965068
10	115.4	2187.2	23.39605459

From the above data, the relation between the no. of primes used in RSA and the observed encryption and decryption times can be illustrated as in fig. 13.

Clearly, there is increase in both times as the number of prime numbers is increased. However, the increase in decryption time is much more drastic than the encryption time (Fig. 14). From the graph we can infer that combining DES with multi-prime RSA becomes less and less feasible as we increase the number of prime numbers in the RSA section.

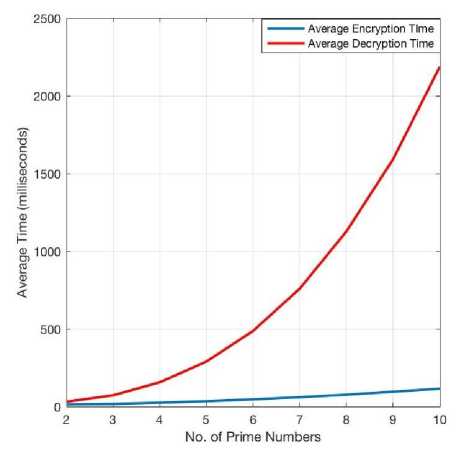
Fig.13. Plot of Avg. Encryption and Decryption time of the RSA+DES Program with Different Number of Primes.

Averaqe Memory Consumed (MB)

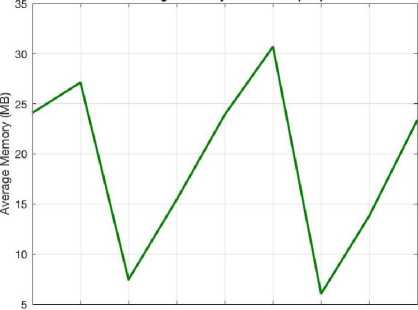
23456789 10

No. of Prime Numbers

Fig.15. Plot of Avg. Memory consumed by the RSA+DES program w.r.t no. of primes used in the RSA.

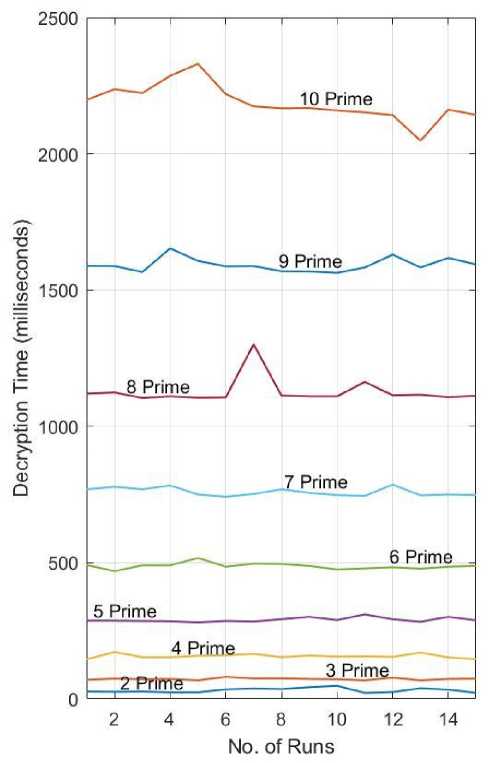
Fig.14. Plot of Decryption times of the RSA+DES Program with Different Number of Primes.

We can also observe the memory consumption with respect to the change in the number of primes in Fig. 15.

What seems like a meaningless trend at first, shows the following vague pattern on closer examination: the consumption for 4 and 8 primes is comparable, for 2, 6 and 10 is comparable, for 5 and 9 is also comparable, and 3 and 7 seem separate with no similar consumption figures. (The word ‘comparable’ has been used here to put together readings with difference less than 1.7 MB)

If we further exclude the standard, i.e. 2 prime RSA from this analysis, we observe that the similarity is occurring at a difference of 4, in the number of primes used. The exception to this is the 3 and 7 prime consumption values, which seem to have more difference than the rest of the 4-difference pairs. However, we also need to consider that with this vague trend, experimentation with up to 10 prime numbers is not enough to draw actual conclusions.

• VI.    Future Scope

The rate of change of time with respect to the number of prime numbers in the multilevel algorithm is clearly illustrated in the above graphs. We have experimented with 10 prime numbers and all follow a similar time complexity pattern However, the same cannot be said for the memory usage of the multilevel algorithm.

The memory usage, roughly, alternatively varies with increase of prime numbers, or with a difference of 4, as explained in the previous section. Due to lack of a clear pattern in memory usage, experimentation with more number of primes is required to get a clear picture of a trend, if any.

• VII.    Limitations

As the prime numbers are increased in the RSA public key encryption, it is observed that the experimental values of encryption time, decryption time, and memory consumption become more and more inconsistent and varying. To illustrate this more clearly, Table 2 presents the experimental values for the 10 prime case.

Table 2. Encryption, Decryption Time Values, and Memory Consumption of Combined 10-Prime RSA and DES.

Sr. No.	Encryption Time	Decryption Time	Memory Consumption
1	113	2198	19.089691162109375 Mb
2	116	2237	22.889625549316406 Mb
3	113	2223	23.53436279296875 Mb
4	111	2286	28.833465576171875 Mb
5	121	2330	27.58641815185547 Mb
6	114	2219	22.204750061035156 Mb
7	113	2174	18.764930725097656 Mb
8	115	2167	20.98853302001953 Mb
9	115	2168	22.851524353027344 Mb
10	121	2159	24.183029174804688 Mb
11	116	2152	20.977310180664062 Mb
12	116	2142	22.871498107910156 Mb
13	106	2048	24.81622314453125 Mb
14	123	2162	26.0682373046875 Mb
15	118	2143	25.281219482421875 Mb

Further, actual memory consumption and time values are largely dependent on the processor capabilities of the system used. The data illustrated in this paper has been compiled on the Mac OS, but the values will change if another OS/processor is used. At the same time, it is important to note that the trends of increase and decrease in values would essentially remain the same.

• VIII.    Conclusion

A widely used public key encryption algorithm, RSA, when combined with a symmetric key algorithm, DES, has its perks, but when Multi-Prime RSA is combined with DES, it definitely proves to be advantageous [15]. The decryption time of Multi-Prime RSA, especially 3-Prime and 4-prime is much more than the decryption time of standard RSA. The major disadvantage of DES is the limited key size, hence, it can be deciphered through brute-force attacks. The multi-level RSA and DES overcome this disadvantage by encrypting the DES key, therefore, making it more secure and reliable. As shown in graphs in section IV, the decryption time significantly increases as number of primes increase, but as compared to it the encryption time increases at a much slower pace. Also, the memory utilization alternatively increases and decreases as we move from 2 to 10 prime numbers. Under the binate protection of DES and Multi-Prime RSA, the data becomes more secure.

Acknowledgment

We sincerely thank our guide and mentor, Surinder Kaur, Assistant Professor at BVCOE, for her immense support and guidance, and for constantly giving us sound advice and motivation.