Study of performance evaluation of binary search on merge sorted array using different strategies

Nowadays, there is an increasing interest in developing parallel algorithms implemented with MPI and Open-MP libraries, to achieve better performance. Very few parallel algorithms achieve comparable optimal performance speed-up, have a near-linear speed-up for small numbers of processing elements and are dependent on the number of processors used [13][2][4]. Programmers must find the best locations in the application, where work load can be divided equally, can run concurrently and determine exactly which threads can communicate with each other [5] [13].

Search algorithm is one of the fundamental fields implemented in previous research. All the search algorithms work well on most sets set of data, but may encounter a set of data for which the performance is not ideal [10]. There are many search algorithms available to use, searching for data that is different in performance and efficiency, depending on the data and on the manner in which they are used. The efficiency of a search algorithm is measured by the number of times a comparison of the search key is done in the worst case. Binary search is the most efficient of all the searching techniques. The concept of efficiency is important when used to determine how fast such a task can be completed [3] [10].

In this paper, we have studied the performance evaluation of binary search on merge sort array, in terms of efficiency, by comparing the results of implementation in three strategies: sequential, multithread and parallel.

Binary search is a ‘divide and conquer’ search algorithm. The ‘divide and conquer’ approach means, that the problem is divided into several small sub-problems, then the sub-problems are solved recursively and combined to get the solution of the original problem. Binary search looks for a particular item, by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. If the middle item is greater than the item, then the item is searched in the subarray to the left of the middle item. Otherwise, the item is searched for in the sub-array to the right of the middle item. This process continues on the sub-array as well, until the size of the sub-array reduces to zero [12]. Binary search, also known as logarithmic search, finds the position of a target value within a sorted array. Binary search runs in at worst logarithmic time, making O (log n)

comparisons, where n is the number of elements in the array [21].

Merge sort is a ‘divide and conquer’ sorting algorithm. In merge sort, there are a series of three steps: divide, conquer and combine. Initially divide the given array consisting of n elements into two parts of n/2 elements each. Sort the left part and right part of the array recursively. Merge the sorted left part and right part to get a single sorted array [6][7][8][9]. Merge sort runs in at worst logarithmic time, making O (n log n) [22]. Fig. 1 shows the sequential merge sort consisting of an array of 4 elements to be sorted. Merge sort in sequential, is based on the fact that the recursive calls run in serial, with the time complexity (1):

T(n) = Θ (n log (n)) + Θ (n) = Θ (n log (n)) (1)

Multithread merge sort , creates thread recursively, and stops work when it reaches a certain size, with each thread locally sorting its data. Then threads merge their data by joining threads into a sorted main list. Fig. 2 shows the multithread merge sort that have array of 4 elements to be sorted. Merge sort in multithread is based on the fact that the recursive calls run in parallel, so there is only one n/2 term with the time complexity (2):

T(n) = Θ log(n) + Θ(n) = Θ(n) (2)

A thread is a stream of instructions that can be scheduled as an independent unit. A thread exists within a process, and uses the process resources, since threads are very small compared with processes. Multithreaded programs may have several threads running through different code paths "simultaneously" [11][14][24]. P-thread library is an execution model of (a POSIX C API) that has standardized functions for using threads across different platforms. P-threads are defined as a set of ‘C language’ programming types and procedure calls. . It allows a program to control multiple different flows of work that overlap in time. Each flow of work’s creation and control over these flows is achieved by making calls to the POSIX Threads API [24].

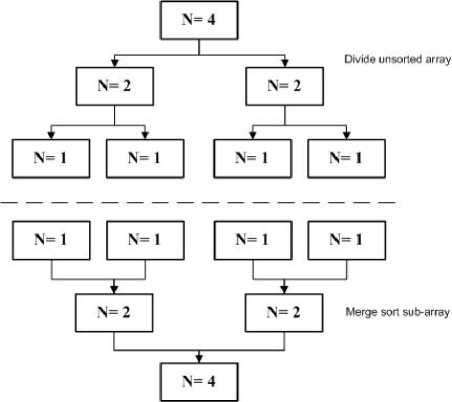
Fig.1. Sequential Merge Sort

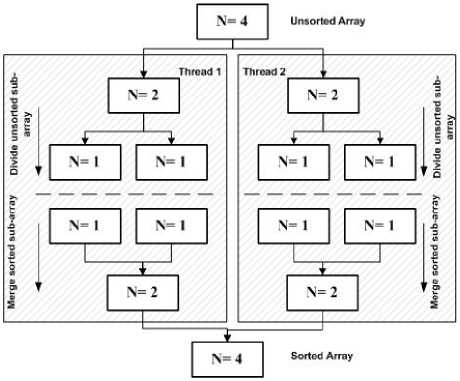
Fig.2. Multithread Merge Sort

Parallel merge sort , is repeatedly split into a main array of parts, having the same size, and each part is processed by a separate processor to the point of having single-element lists. These elements are then merged together to generate sorted sub-lists. One of the parallel processes is designated as a master. This process distributes the data parts among other worker’s parallel processes that use the sequential version of merge sort, to sort their own data. Then sorted sub-lists are sent to the master. Finally, the master merges all the sorted sub-lists into one sorted list [1] [23]. Merge sort in parallel, is based on the fact that the recursive calls run locally on each processor, so there is only one n/p term with the time complexity (3) [6]:

T(n) = O ((n/p) * log(n/p)) + O(n) (3)

Message Passing Interface (MPI) is widely used to implement parallel programs [1]. MPI standard has been designed to enhance and reduce the gap between the performance by a parallel architecture and the actual performance [1] [21][22]. MPI offers several functions, including send/receive operations. There are also several implementations used in writing MPI programs, one of which is parallel virtual machine. Parallel Virtual Machine (PVM), is a software package that permits a heterogeneous collection of UNIX or Windows computers, hooked together by a network, to be used as a single large parallel computer [1][23][24].

Combining both binary search and merge sort algorithms, using function methods. In this paper the algorithm is created with three different strategies, using a generated random array dataset: sequential, multithread and parallel. A sequential code, executing on a single processor can only perform one computation at a time. Whereas the multithread and parallel code is executed in parallel and divide up perfectly among the multi-thread and multi-processors. The main objective of this algorithm is to study and evaluate the performance execution time and speed up.

The results were conducted using IMAN1 supercomputer [20] which is Jordan's first and fastest supercomputer. It is available for use by academia and industry in Jordan and the region and provides multiple resources and clusters to run and test High Performance Computing (HPC) codes.

The remainder of the paper is organized as follows: Section 2 presents related work. Section 3 presents experimental and result evaluation. Section 4 presents conclusion and future work.

• II.    Related Work

There has been little work done to parallelize the search algorithms, using different strategies and parallel architectures. In [10] the author’s study is an evaluation of critical factors affecting the efficiency of searching techniques. They conclude that numbers of comparisons is the most critical factor affecting the searching techniques. They also show that binary search is the most efficient of all searching techniques.

With reference to [6] the author’s studies of performance evaluation of parallel quicksort, parallel merge sort, and parallel merge-quicksort algorithms in terms of running time, speedup, and efficiency using open MPI library and the experiments conducted used IMAN1 supercomputer, findings were as follows: Parallel Quicksort has better running time for both small and large data size, followed by Merge-Quicksort and then Merge sort algorithms.

“Ref. [15]”, the author’s has proposed work comparison of both single and multicore implementation of number searching and sorting for a large database. The results presented show that the multicores achieve better speed up over single core. Multi-core reduced the time for executed multiple threads in parallel.

• III.    Experimental and Evaluation Results

We have implemented binary search algorithm in three different scenarios: sequential code, multithread code and parallel code, for binary search using merge sort and random array dataset. We used IMAN1 supercomputer to prepare experimentation to evaluate performance execution time and speed up. The experiments were conducted on different data set sizes, to find out the best execution time and efficient results. First, the sequential code was executed and the time taken for three positions: generate random array, sort the random array, and search the item on sorted array. Second, the multithread code was executed and the time taken for about the same positions of sequential code which can be divided into threads using p-thread compiler. Third, the parallel code task was divided into sequential code segments, using an MPI compiler, which each segment runs on, with an individual processor. Then we calculated the execution time in each scenario of algorithm, to evaluate efficiency and determine which one has the best performance execution time and speed-up in different scenarios.

• A.    IMAN1 Supercomputer

  IMAN1 is first Jordan's national supercomputer project started in January 2010. IMAN1 system is the fastest high performance computing resource, funded by JAEC and SESAME and it completely developed in house by Jordanian resources. IMAN1 is using in academic and industry in Jordan and region [16]. IMAN1 using 2260 PlayStation3 devices which have performance of 25 Tera FLOPS (25 x 1012 Flops i.e. 25 Trillion Floating Point Operations Per Second) [20].

• B.    Design Code and Implementation

The experiment was done by IMAN1 supercomputer center. We did our project in three scenarios. First, we combined both binary search and merge sort in sequential code. Then we implemented both binary search and merge sort with a multithread method. Finally, we implemented both binary search and merge sort, under parallel method, using an MPI compiler. The sequential, multithread and the parallel codes are explained below.

Sequential Code

Main function() with (stdio.h, stdlib.h and time.h) and define the size of array:

Step 1: Declare functions and variables to store allocated memory.

Step 2: Start the timer. clock_t start = clock();

Step 3: Declare srand to fill array with random numbers.

Step 4: Partition and divide unsorted array into subarray.

Step 4: Sort and merge the subarray into sorted array.

Step 5: Print sorted array.

Step 6: Find item within sorted array by use binary search, and then print if found item successful or not with position of item.

Step 7: End the timer. clock_t stop = clock();

Step 8: Calculate the difference in start and end time. diff = ( end – start ) *1000 / CLOCKS_PER_SECOND;

Step 9: Return 0.

Multithread Code

Main function() with (stdio.h, pthread.h, stdlib.h and time.h) and define: (size of array, number of thread and struct node)

Step 1: Declare functions and variables to store allocated memory.

Step 2: Start the timer. clock_t start = clock();

Step 3: Fill array with random numbers.

Step 4: Define node and create threads for partition and divide unsorted array.

Step 5: Join thread to sort and merge the subarray into sorted array.

Step 6: Print sorted array.

Step 7: Find item within sorted array by use binary search, and then print if found item successful or not with position of item.

Step 8: End the timer. clock_t stop = clock();

Step 9: Calculate the difference in start and end time. diff = ( end – start ) *1000 / CLOCKS_PER_SECOND;

Step 10: Return 0.

Parallel Code

Main function() with (stdio.h, mpi.h, stdlib.h and time.h) and define the size of array:

Step 1: Declare functions and variables to store allocated memory.

Step 2: Start the timer. clock_t start = clock();

Step 3: Create and populate the array by fill array with random numbers.

Step 4: Initialize MPI.

Step 5: Divide the unsorted array in equal-sized chunks.

Step 6: Send each subarray to each process.

Step 7: Perform the merge sort on each process.

Step 8: Gather the sorted subarrays into one.

Step 9: Make the final merge sort call.

Step 10: Print the sorted array

Step 11: Find item within sorted array by use binary search, and then print if found item successful or not with position of item.

Step 12: End the timer. clock_t stop = clock();

Step 13: Calculate the difference in start and end time. diff = ( end – start ) *1000 / CLOCKS_PER_SECOND;

Step 14: Clean up root.

Step 15: Clean up rest.

Step 16: Finalize MPI.

• C.    Performance Evaluation and Results

Table 1, shows software and hardware requirements and table 2 shows algorithms and the parameters used:

Run Time Evaluation

Tables 3, 4, 6, 7, and 8 show running time test code for each strategy to different dataset size. All results are performed on: 2, 4, 8, 16, 32, 64, 128, 143 processors. As illustrated in the tables, as the data size increases, the run time increases too, due to the increased number of comparisons and the increased time required for data splitting and gathering in a parallel strategy. Sequential code has the best run time for small dataset, while parallel code is the best in large dataset size, followed by sequential code and then multithread code. Finally, multithread code has the worst run time results.

Table 3. Test Data Set Size (489)

Sequential Algorithm		Multithread Algorithm		Parallel Algorithm
Run Time (MS)	Up to	Run Time (MS)	Up to	Run Time (MS)	Processor
0	1	1120	2 Thread	30	2
				50	4
				120	8
				130	16
				250	32
				130	64
				220	128
				200	143

From table 3 shows that the sequential code has better running time in a small dataset, followed by parallel code and then multithread code.

Table 1. Software and Hardware Requirements

Software and Hardware	Type
Virtual tools	Oracle VM VirtualBox and IMAN1 system
Operating System	Windows 10 64-bit and Linux 6.4
Languages	C Language
Hardware	IMAN1 Supercomputer center
Specification	Intel core(TM) i7-4720HQ CPU 2.6GHz 16GB
Library interface	stdio, stdlib, time, pthread, and mpi

Table 2. Algorithms and Parameters are used

Parameter	Type
Algorithms	Binary search and merge sort
Size of data set	489, 10000, 50000, 250000, 500000 and 1000000
Number of processor	1, 2, 4, 8, 16, 32, 64, 128 and 143
Strategy of scenario	Sequential, multithreaded, and parallel
Array dataset	Random number generation
Measurement	Execution time and speed up

Table 4. Test Data Set Size (10,000)

Sequential Algorithm		Multithread Algorithm		Parallel Algorithm
Run Time (MS)	Up to	Run Time (MS)	Up to	Run Time (MS)	Processor
10	1	Unable to create thread	2 Thread	0	2
				60	4
				150	8
				70	16
				130	32
				70	64
				300	128
				130	143

From table 4 shows that the parallel code at two processors has better running time at 10,000 elements, followed by sequential. However, in this case the multithread code could not create threads.

Table 5. Test Data Set Size (50,000)

Sequential Algorithm		Multithread Algorithm		Parallel Algorithm
Run Time (MS)	Up to	Run Time (MS)	Up to	Run Time (MS)	Processor
80	1	Unable to create thread	2 Thread	120	2
				40	4
				120	8
				220	16
				220	32
				180	64
				240	128
				280	143

Table 7. Test Data Set Size (500,000)

Sequential Algorithm		Multithread Algorithm		Parallel Algorithm
Run Time (MS)	Up to	Run Time (MS)	Up to	Run Time (MS)	Processor
910	1	Unable to create thread	2 Thread	470	2
				560	4
				420	8
				580	16
				530	32
				770	64
				760	128
				800	143

From table 5 shows that the parallel code at four processors has optimal running time at 50,000 elements, followed by sequential, also, in this case the multithread code could not create threads.

Table 6. Test Data Set Size (250,000)

Sequential Algorithm		Multithread Algorithm		Parallel Algorithm
Run Time (MS)	Up to	Run Time (MS)	Up to	Run Time (MS)	Processor
490	1	Unable to create thread	2 Thread	180	2
				180	4
				280	8
				340	16
				360	32
				350	64
				610	128
				390	143

Table 6 shows that the parallel code at two and four processors, has optimal running time at 250,000 elements, and has better running time up to 143 processors compared with sequential, except the case of 128 processors; again, in this case the multithread code could not create threads.

Table 7 shows that the parallel code at 8 processors has optimal running time at 500,000 elements, and has better running time at up to 143 processors compared with sequential, but there exist some differences in running time among processors, due to the delay of entire communication of functions and remote connection network.

Table 8. Test Data Set Size (1000,000)

Sequential Algorithm		Multithread Algorithm		Parallel Algorithm
Run Time (MS)	Up to	Run Time (MS)	Up to	Run Time (MS)	Processor
1870	1	Unable to create thread	2 Thread	760	2
				750	4
				920	8
				1070	16
				1230	32
				1260	64
				1280	128
				1580	143

Table 8 shows the parallel code at 4 processors has optimal running time at 1000,000 elements, and has better running time up to 143 processors compared with sequential, but there exists some differences in running time among processors, due to the delay of entire communication of functions and remote connection network.

Table 9 shows comparisons of optimal running time between sequential and parallel code. Table 3.10 shows a comparison of the optimal number of processors, with growth of dataset size.

Fig. 3 illustrates the run time, according to different dataset sizes in both sequential and parallel algorithms, the general behavior for two algorithms as the size of dataset increases that run time is increased in both algorithms, but that the parallel has the best run time results, due to better load distribution among more processors.

Table 9. Sequential and Parallel Running Time Comparison

Dataset Size	Sequential Algorithm	Parallel Algorithm
	Run Time (MS)	Optimal Run Time (MS)
489	0	30
10,000	10	0
50,000	80	40
250,000	490	180
500,000	910	420
1000,000	1870	750

Table 10. Number of Processors with Dataset Size

Dataset Size	Optimal Number of Processor
489	2
10,000	2
50,000	4
250,000	4
500,000	8
1000,000	4

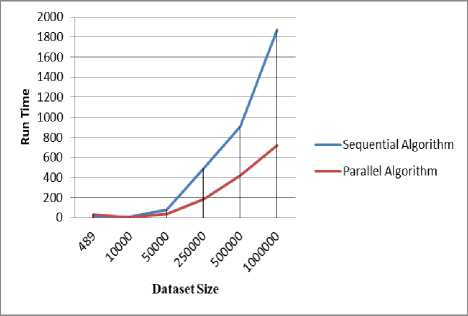
Fig.3. Sequential and Parallel Running Time Comparison

Speed up Evaluation

The speed-up is the ratio between the sequential time and the parallel time [6]. Table 11 and Fig. 4 illustrate the speed-up of the parallel code on 2, 4, 8, 16, 32, 64, 128 and 143 processors with 50,000, 250,000, 500,000 and million dataset sizes, respectively. The results show that parallel code achieves the best speedups values, up to 2.72. The speed-up defined as equation (4):

Speed up =

Run time using sequential code Execution time using a parallel with p processors

Table 11. Speed up of Different Datasets with Different Number of Processors

No. of Processor	Speed up of 50,000	Speed up of 250,000	Speed up of 500,000	Speed up of 1000,000
2	0.67	2.72	1.94	2.46
4	2.00	2.72	1.63	2.49
8	0.67	1.75	2.17	2.03
16	0.36	1.44	1.57	1.75
32	0.36	1.36	1.72	1.52
64	0.44	1.40	1.18	1.48
128	0.33	0.80	1.20	1.46
143	0.29	1.26	1.14	1.18

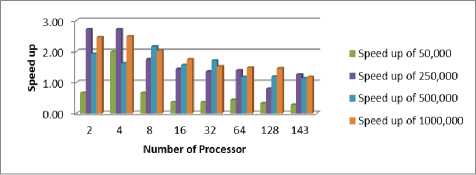
Fig. 4. Speed up of Different datasets with Different Number of Processors

From fig. 4 illustrate the speedup of the parallel codes on 2, 4, 8, 16, 32, 64, 128, and 143 processors is the best done between 50000 and 500000 dataset size, respectively.

• IV.    Conclusions

  We conduct binary search on merge sort experimental by three different strategies: sequential, multithread and parallel on IMAN1 supercomputer. The results obtained from the experimental analysis performance execution time and speed up, the combine binary search and merge sort algorithms with parallel code performs better than the sequential and multithread code after 489 elements, followed by sequential and then multithread. As the array size becomes large then the number of processor increase. Multithread code used p-thread, but parallel written with MPI library. Moreover, the speedup of the parallel codes on 2, 4, 8, 16, 32, 64, 128, and 143 processors is up to 2.72, and the best is done between 50000 and 500000 dataset sizes, respectively. The future of this work seeks to use binary search on other sorting algorithms to evaluate performance in terms of execution time and speed up. And use other methods with multithread code such as MPI library.

Acknowledgment

We would like to acknowledge eng. Zaid Abudayyeh for his support to accomplish this work.