Study of pulsating flow of viscous two-phase media in a flat porous pipe considering particle gravity force

DOI:

Recently, the interest of researchers in the issues of pulsating flow of single- and multiphase media has increased significantly. Scientific interest in this problem is due to the fact that pulsating flows of mixtures are becoming increasingly widely used in many branches of human activity. Similar processes are often observed in the food and chemical industries, in the processes of extraction, dissolution, drying, crystallization, as well as when cleaning the internal surfaces of equipment pipes from deposits and sediments.

In addition, in pulsating flows, at appropriate frequencies and amplitudes of fluid flow oscillations, the area of turbulence can be significantly moved away, hydraulic resistance can be reduced, the flow rate can be changed, the filtration of liquid through the permeable wall of the pipeline can be accelerated, and the processes of extraction of essential oils, medicines, synthetic materials, etc.

Although a large number of scientific papers have been published on the hydrodynamics of pulsating flows, many issues have not yet been sufficiently studied. These include, for example, the unsteady movement of pulsating flows of multiphase media in pipes with porous walls. Individual works and theories for studying these processes are usually based on the use of simplified models.

THEORETICAL BASIS

Let us consider the unsteady two-dimensional pulsating motion of a viscous two-phase medium in a flat pipe with porous walls. Let us choose a Cartesian coordinate system so that the axis is directed along the bottom wall of the pipe. Let's place the origin of coordinates at the intersection of the bottom wall and the inlet section.

In the hydrodynamic formulation, we will study the flow process on the basis of a system of dimensionless two-dimensional unsteady equations of motion of two-phase media for a plane flow in an interpenetrating model taking into account gravity, the continuity equation for phases and the mixture concentration ratio [1-4]:

ди      1 ди      ди,

^^Та^в^

М 1 дР

ai fi L дх2 +

+ — ai

[А_д_[,.ди1|+^_[,.дУ-

3L2 дх2  i дх2    дх1  i дх1

2 д

3L дх2

г диа  1 д г дгя| к^ ^д^кд^]]+

+ ^iK(U3-i —Ui) + Fr2f1;                            (1)

дUi       1 дVi       дVi     М 1 дР

fl"aT + fiUi LдX2 + f‘ViдX1'1 = -atf‘LдX~2 +

+- [1-д- [fi ди]+4 ^[fip]+1^[fi д^] -l^[fi ^1]] + ai L2 дх2   дх2   3 дх1   дх1   L дх2   дх1   3L дх1   дх2

+ "^tK(V3-i-Ui) + Fr2fV;                            (2)

df ft Ifi _ q dt    dx1    L dx2      '

f1 + f2 = 1; i = 1,2.

To solve the given system of equations, it is necessary to formulate the initial and boundary conditions. A flat pipe with porous walls may have either a top or bottom permeable wall. A schematic picture of such flat-porous pipes is shown in Figure 1.

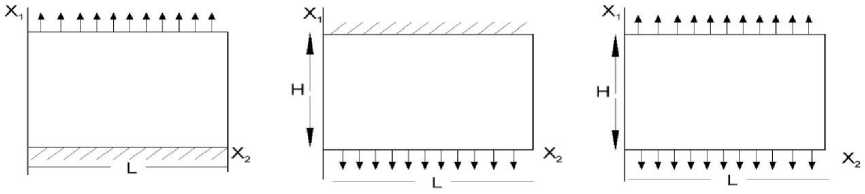
Figure 1. Schematic picture of flow in a flat-permeable pipe

Let a flat pipe have a permeable upper wall. At the initial moment of time, the two-phase mixture is at rest. Starting from t>0, pulsating motion occurs due to the periodicity of the pressure gradient at the inlet of the pipe.

Then the initial and boundary conditions will take the following form:

at t = 0: Ui = 0, ut = 0, ft = ft0 for 0 < x1 < 1, 0 < x1 < 1;

at t > 0: %2 = 0: P = P0 + Л cos cot, f1 = ft0, vt = 0,

ut = u01G4(at) cos cot + В (at) sin o t), u2 = xu, for 0 < x1 < 1;

at x, = 0: du1/u2 = 0, ut = 0 for 0 < x, < 1;

at %2 = 0: ut = 0, vt = 0 for 0 < x2 < 1;

at x1 = 1: ut = 0, V1 = a(1 — f2|%=^)(P - Pc) for 0 < x2 < 1;

If a flat pipe has a bottom permeable wall, then the condition for the permeability of the liquid phase is set at x 1 =0 for 02<1. Taking into account the process of blocking small holes in the permeable wall, this condition will be written as

^1 = a(1 - f2|x=H)(P - Pc).

For flat pipes having top and bottom porous walls, the permeability condition will exist for both the top and bottom walls. Under such initial and boundary conditions, we solve the system of equations (1) - (4) using the iterative method of alternating directions at ξ=0.

It is necessary to obtain a qualitative picture of the flow, i.e. changes in the velocity field, phase concentration and pressure depending on α i , Fr 2 , μ 1 ⁄μ 2 , K, a.

RESULTS AND DISCUSSION

Let us consider the change in the longitudinal velocities of a two-phase flow in the section X 2 = 0.5 of a flat pipe having upper and lower porous walls at « 1 = 2.2, « 2 = 0.84, Re_t = 459, Re 2 = 66, Fr 1 = l^M = 0.06, a = 10^-3,K = 60.

The longitudinal components of the velocities of the first (solid line) and second (dotted) phases for ω t=0 (1) and ω t= π /3 (2) are shown in Figure 2. In the initial section, the phase velocity profiles coincide, because in the calculations, λ=1 was assumed. With distance from the inlet section, the more viscous phase begins to lag behind the less viscous one, and the profiles tend to be parabolic. A similar pattern was established for axisymmetric pipes, where at low pulsation frequencies the profiles tend to a parabolic shape. Numerical experiments have shown that at low pulsation frequencies, particles of the second phase begin to settle in the lower part of the pipe due to gravity. This process to some extent affects the symmetry of the phase velocity distribution. In the upper part of the flat pipe, the velocities μ will be greater than at the corresponding points in the lower part of the pipe.

The longitudinal components of the velocities of the first (solid line) and second (dotted) phases for ω t=0 (1) и ω t= π /3 (2) are shown in Figure 2. In the initial section, the phase velocity profiles coincide, because in the calculations, λ=1 was assumed. With distance from the inlet section, the more viscous phase begins to lag behind the less viscous one, and the profiles tend to be parabolic. A similar pattern was established for axisymmetric pipes, where at low pulsation frequencies the profiles tend to be parabolic [5,6]. Numerical experiments have shown that at low pulsation frequencies, particles of the second phase begin to settle in the lower part of the pipe due to gravity. This process to some extent affects the symmetry of the phase velocity distribution. At the top of a flat pipe, particle velocities will be greater than at the corresponding points at the bottom of the pipe.

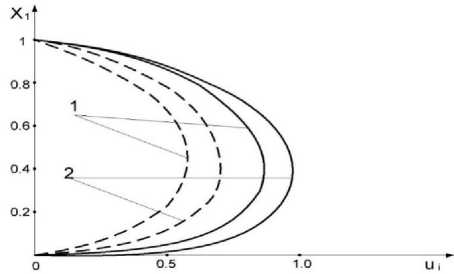
Figure 2. Longitudinal velocity profiles in a flat permeable pipe.

Xi

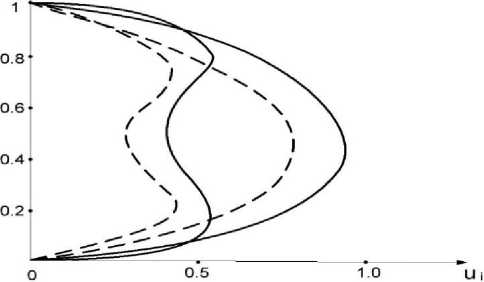
Figure 3. Change in longitudinal velocity profiles in a flat pipe with a permeable bottom wall.

• Figure 3    shows the manifestation of the Richardson effect in a flat pipe with a permeable bottom wall. The solution was obtained with α 1 =6, α 2 =2.24, Fr 2 =l; α=10^-3; for х 2 =0,5; ω t= π /12 (1), ω t=0 (2). Comparing the curves, we see that with the formation of the Richardson effect, the maximum value of the relative difference u1-u2 moves from the axis closer to the wall [7,8].

The permeability of the wall reduces the total resistance of the pulsating flow. With an increase in the permeability coefficient, the pulsating flow can turn into non-pulsating laminar movement.

Therefore, if it is necessary to weaken the flow pulsation, then it is necessary to create an additional permeable inner wall of the pipe.

Numerical experiments have shown that to reduce the degree of siltation of a permeable pipe, the frequency of pulsation of the mixture along the flow should be increased.

In the near-wall region of the upper and lower porous walls, a decrease in the volumetric content of the second phase is observed. In this case, the rates of liquid penetration through the upper and lower pores of the wall are almost equal.

• Figure 4    shows the change in the rate of liquid infiltration along the length of a flat pipe with a lower porous wall. Curve 1 was obtained at α 1 =8, α 2 =3.05, and curve 2 at α 1 =2,2; a 2 =0.84; with the same values of the other parameters, when Fr 2 =l; ^ 1 /^ 2 = 0.062, К=50, a=10^-3.

It can be seen that the rate of seepage along the length of the pipe decreases. At small values of α, particles of the solid phase begin to settle on the walls of the pipe and thereby intensify the process of clogging the pores of the porous wall. This pattern confirms the advisability of taking into account the dependence of the permeability coefficient on f 2 | x=0 .

As the permeability coefficient increases, the internal pressure approaches the ambient pressure, and the seepage length decreases. Figure 5 shows the pressure distribution across the layers of a flat pipe with a permeable bottom wall. The solution was obtained with the same initial data for α 1 =2,2; α 2 =0,84; the numbers correspond to the pipe layer. In a permeable pipe, the pressure inside the pipe is less than in an impermeable pipe. This is due to the fact that in a permeable pipe the pressure loses its strength to overcome the resulting additional pressure gradient caused by the permeability of the wall. This effect is confirmed in other works [9, 10].

Let us consider the redistribution of concentration in a flat pipe with porous walls taking into account gravity. In Fig. Figure 6 shows graphs of the distribution of the volume concentration of the carrier phase in the section х 2 =0,6 of a flat pipe with a lower permeable wall. Curve 1 was obtained at α 1 =2,2; α 2 =0,84; and curve 2 at α 1 =8; α 2 =3,05; for Fr 2 =l; К=60; ^ 1 /^ 2 =0.062; a =10 -3 ; X 2 =0.6; m l 0. Permeability affects the flow concentration; the symmetry of the distribution is disrupted.

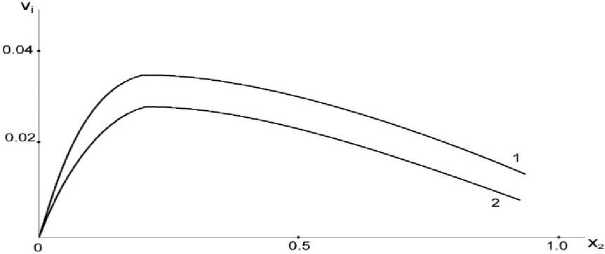
Figure 4. Variation in the rate of liquid infiltration along the length in a flat pipe with a permeable bottom wall.

The movement of the mixture near the pipe wall is unstable with respect to the flow parameters. With increasing pulsation frequency (hence, with increasing a;), the volumetric content of the carrier phase at the permeable wall increases. From curve 2 it is clear that at low pulsation frequencies, solid particles settle on the permeable wall and, thereby, displace liquid particles. This process leads to a decrease in the rate of liquid penetration through the pores of the wall and reduces the pressure gradient at the permeable pipe wall.

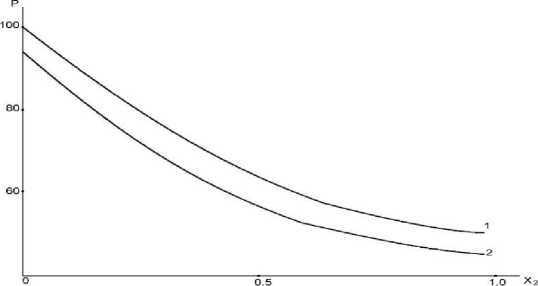
Figure 5. Pressure distribution in a flat pipe with a permeable bottom wall.

Figure 7 illustrates the change in the volume concentration of the more viscous phase in the initial sections of a flat pipe with upper and lower permeable walls. The numbers correspond to the pipe cross-section. The picture of the f 2 distribution in sections of a flat porous pipe was obtained when the Richardson effect took place. The calculation was made for « , = 8, « 2 = 3.05, Re 1 = 411, Re 2 = 3.05,для Fr 2 = 1, К = 60, ^M = 0.062,a = 10^-3, to t=0.. From the calculation results it is clear that from the initial cross sections f 2 undergoes large fluctuations. As we move away from the inlet section, the two f 2 peaks formed in the flow core gradually smooth out. In this case, the oscillatory nature of the concentration distribution is preserved.

Calculations have shown that at low pulsation values, the rate of liquid leakage through the upper porous wall is greater than through the lower one. This is due to the fact that near the upper permeable wall the concentration of solid particles is less than near the lower one.

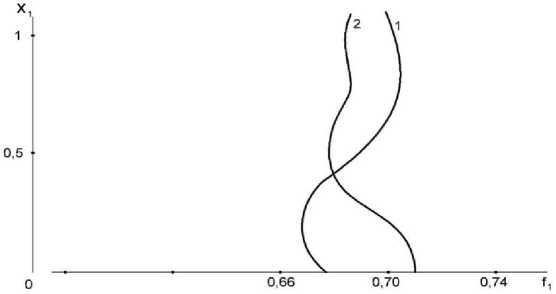
Figure 6. Distribution of the volumetric content of the carrier phase in a flat pipe with a permeable bottom wall.

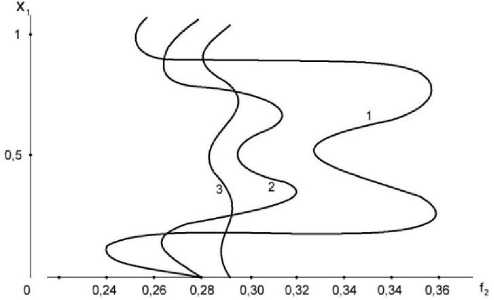
Figure 7. Distribution of volume concentration of the solid phase in the initial sections of a flat permeable pipe.

CONCLUSION

With a pulsating flow of two-phase media in a flat porous pipe, increasing the Womersley frequency parameter, the speed of particle transfer near the wall increases, and in the core of the flow there is practically no transfer of particles. A significant increase in the transfer of inclusion particles is observed during the flow of a less viscous phase. With low-frequency pulsations, a zone of highly concentrated mixture is formed in the near-pipe area. An increase in the pulsation frequency leads to a displacement of this zone in the direction of the axis and, thereby, forms a slightly concentrated mixture in the near-wall region.

The results obtained confirm the conclusion that it is necessary to take into account the influence of gravity of solid particles and the variability of the permeability coefficient on the nature of the distribution of phase concentrations, speed and pressure when the mixture moves in a flat porous pipe.