Study on the Mainardi beam through the fractional Fourier transforms system

да

W (z ) = E n=0

n ! F ( X n + ц )

F ( z ) = t -( - z )^ t? n ! F ( -v n )

( — z ) n ^-1 .                  z

-------Г ( v n + 1) sin ( nv n ), n !

1 ”

= 1 V

^П n = 1

M. .( z ) = У----------

Й n ! F ( -v n + (1 -v ))

( - z ) n ^{- 1}

= — V------ F ( v n )sin( nv n ).

n n = 1 ( n - 1)!

A noteworthy particular case is

M 1/2 ( z ) = -U exp ( - z 2/ 4), V n

M _V 3 ( z ) = 3 2/3 Ai ( z / 3¹³).

M denotes the Mainardi function that it is here, like an Airy function. Ai denotes the Airy function that writes as follows: [20]

Ai ( z ) = ¹ J cos ( z ^ + 3 ^ ³ ) d t . ⁿ 0

We exert Mainardi function in calculation and descript it. Mainardi beam in the Cartesian space as follows.

_ z                  I x ।      I ax 1       I y I      I ay IE (x, y ) = M1J — I expl — IM1J — I expl — I. (7)

I ^x 0 J    I ^x 0 J      I y 0 J    I y 0 J

The Mainardi beam are described in details with the number, height, and width of the peaks that depend on the factors x 0 and a . M 1/ q ( z ) satisfies the differential equation of order q –1 [19].

”.

=12

^П n = 1

M , q (Z) = £ — n = 1 n ! Г

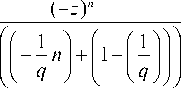
( - Z ) n ^{- 1} ( n - 1)!

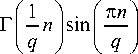
E ( x , У , z ) =

ik     I ax   ia ² z ay   ia ² z

=----exp I +--+--+--

2 n z    ( x 0    2 kx 2 y 0    2 ky 2

x

^^^^^^B

y

^^^^^^B

Mainardi beam in the FFT and the FrFT systems

The Fresnel integral is tool for describing of the beam propagation in free space (FFT system).

Fresnel integral of a Mainardi beam is as follows [20].

d x 1 d y 1 =

^^^^^^B

x

^^^^^^B

iaz 11

x 0 k

M 1 I     I dx 1 x q I x 0 J

iaz | I

y 0 k

M Д1 d y l q l У 0 J

Since the relationship between the primary and last page variables is determined by using Fourier transform and the convolution [21], we note the convolution of two functions, f 1 ( т ) and f 2 ( t ).

f l ( t ) ® f , ( t ) =

= M 1

q

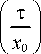
I ik 2

® exp     t ²

l 2 z

”

= J f 1 ( x i ) f : ( t- x 1 )d x 1

-”

Where t = x - iaz / x ₀ k or t = y - iaz/y ₀ k . The convolution theorem of the Fourier transform has the following property [20].

”

f 1 ( t ) ® f 2 ( t ) = J f 1 ( 4 ) f 2 ( 4 )exp ( - i 4t ) d 4        (11)

-”

We must introduce a new function for the Fourier of f , ( t ). The familiar Mittag-Leffler function E _a ( z ) introduced by the Mittag–Leffler [22] and its generalization E a ( z ) introduced by Wiman [23] are defined by the following formula:

E a ( z ) = 2 ”= ₀ z n / r( a n + 1) = E a ,1 ( z ). (12)

As well-known in probability theory, the Fourier transform of a density provides the so-called characteristic function. In this case we have:

F [ 1/2 M v ( | x | ) ] =

=    cos( kx ) M _v ( x )d x = E_{2 v}(- k ²).

Where M ν ( z ) denotes the Mainardi function and E ν ( z ) denotes the Fourier transform of the Mainardi function (Mittag-Leffler function). Now, we can indicate the Fourier of f , ( t ).

”

/ 1 ( 4 ) = 2

n = 0

4 ⁿ

( qn )!

.

By Eq (6) and by a simple mathematical calculation of Eq (13) and Eq (14), we can demonstrate:

M _V 3 ( z ) / J cos( 4 ³/3 + z 4 )d 4 ,                   (15)

M 1/5 ( z ) / J cos( 4 ⁵/5 + z 4 )d 4 ,                    (16)

M _V 7 / J cos( 4 ⁷/7 + z 4 )d 4 ,,                     (17)

M 1 q / J cos ( 4 q / q + z 4 )d 4 ( q is odd).            (18)

We found that our calculations are similar to the previous calculations of the Airy beam [21]. Therefore, Eq. (9) is found to be

E ( x , y , z ) =

ix 0 y 0

2 n z

I ax 1    | ay । exp I — I exp I — Ix l x0 J    l y 0 J

x

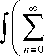
4 ⁿ 1 I iz 4 ² exp--

( qn )! J    l 2 k

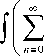
4 ⁿ 1 I iz 4 2 exp--

( qn )! J    l 2 k

^^^^^^»

az 4 I I 14 x +      d4x x 0 k J J

az 4 I 1 4 y + —^ I d 4 .

y 0 k J

The FrFT of various kinds of laser beams have been

widely investigated. The Wigner distribution function is rotated by an angle of ф = p n /2 where p is the power of FrFT. The optical system for performing the FrFT is shown in Figure 1.

Lohmann I system p

(a)

(b)

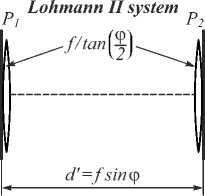
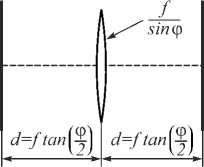
Fig. 1. Optical system for the FrFT: Lohmann I system (a), Lohmann II system (b). Numerical calculations

Figure 1 a denotes the Lohmann I system and Figure 1 b the Lohmann II system; f is the standard focal length. In Figure 1 a , the focus of the lens is f /sin ф . The Lohmann I and Lohmann II optical systems are equivalent and are described by the following transfer matrix [5, 16]:

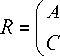
cos ф f sin ф^ sin ф

--cos ф

Mainardi beam passing from a Lohmann optical system, obeys the well-known Collins integral formula:

E ( x , У , z ) =

exp ( ikz )

=---—-exp i XB

ikD ( x ² + y ² )

2 B

да I x I I axi I x M exp exp

-да q V x 0 J    V x 0 J

да x M 1

-да —

q

ik

— ( Ax, ² - 2 xx ) d x ₁ x 2 B^v

У 1 I I ayi I ik ( л i

I exp l — I exp —( Ay i ² . y о J    V У о J    L ² B

- 2 y i y ) d y i .

We note that the convolution of the FrFT system, are f , ( t ) and f i ( t ). Therefore, Eq (2i) rewritten as follows:

2.0

1№

2.0

1^

1.6

1.6

1.2

1.2

0.8

0.4

(1) (a)

лллЛ.

0.8

0.4

X(mm)

-8

(2) (a)

-8 -6 -4 -2 0 2 4 6 8

1.0

0.5

I °

,          exp ( ikz )       ikD ( x ² + y ² )

^E ( x , ^y , z ) = —A— xp —2B—

I ax ay I x exp l--1--Ix

V Ax о Ay о J

I- ikx ² iky ²     ia ² B    ia ² B I

x exp                 1+ x

V 2BA 2BA 2Akx02 2 Aky02 J fTI^ En I   . iBE2 V x  iaB Ц

x             exp(---i E +       dEx

VlVn^ qn)! J  12 kA  \ A  kAx 0 JJ fда^т En I   I iBE2  .J y  iaB ILJ

x               expi E +dE

^J -да V n = 0 ( qn )! J    V   2 kA     V A  kAy 0 J J J

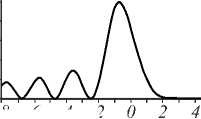
In the following, the properties of Mainardi beams in the FFT and the FrFT systems derived in Section 1 for the parameters are chosen as X =0.53 ц т, f =i000 mm, a = 0.05 and x 0 = y 0 = 1 mm. Figure 2 represents the normalized intensity distribution of a Mainardi beam in the FFT system depending on the parameters q , a , x 0 , and y 0 .

X(mm)

-8 -6 -4 -2

-8

(b)

1.0

0.5

-

2.0

1.6

1.2

0.8

0.4

Ito

X(mm)

-8 -6 -4 -2

-8

(c)

1.0

0.5

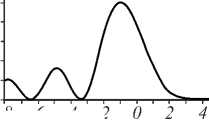
Fig. 2. Normalized intensity in the FFT system; (1) the x-direction of a Mainardi beam and (2) Intensity graph of a Mainardi beam; (a) q = 3, (b) q = 5 and (c) q = 7

Now, we investigate the influence of the parameter q on the normalized intensity distribution. Using Eq (19), we simulate a Mainardi beam in the FFT system. In Figure 2, with increase in the value of q, the number of lateral side lobes decreases, the main peak expands, and the heights of other peaks decrease.

We investigate the influences of the parameters q and p on the contour graph of the normalized intensity distribution for a Mainardi beam in the FrFT system Using Eq (22). Figure 3 represents the contour graph of the normalized intensity distribution of a Mainardi beam in the FrFT system depending on the parameters p , q , a , x ₀, and y ₀. Now, we investigate the influence of the parameters q and p on the normalized intensity distribution.

The variation of the intensity distribution with the fractional power is periodic, and the period is 2. When p < 1, the lateral side lobes are at the left side. In this case, moreover, the spot size of the Mainardi beam decreases with an increase in the value of p and with an increase in the value of q , the number of lateral lobes decreases and the main peak expands and heights of the other peaks decrease. When 1 <  p ≤ 2, the lateral side lobes are located on the right side. In this case, however, the spot size of the Mainardi beam increases with an increase in the value of p , and, with an increase in the value of q , the number of lateral lobes decreases and the main peak expands and heights of other peaks decrease. This dramatic phenomenon can be interpreted as follows: when i < p < 2, A =cos( p n /2) has a negative value, and B = f sin( p n /2) has a positive value.

-8              8-8              8    -8              8

(a)                                             (b)                                                (c)

Fig. 3. Intensity graph in the FrFT system at: (1) p = 0.3 (2) p = 0.5 (3) p = 0.7 (4) p = 1.3 (5) p = 1.5 (6) p = 1.7

and with; (a) q = 3, (b) q = 5, (c) q = 7

-8

(6)    -8

1.0

0.5

О

-8

-8

(a)

(c)

(b)

Continuation of Fig. 3

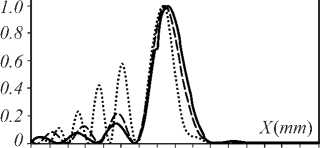
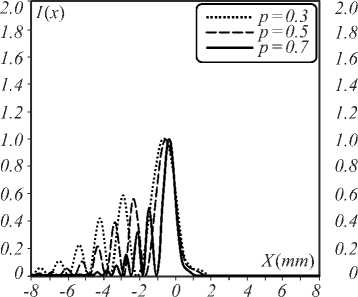
Figures 4 – 6 show the normalized intensities in the x-direction of a Mainardi beam with a different p in the FrFT system for a = 0.05, x0 = y0 = 1 mm, q = 3, 5, and 7. If the power of FrFTs are the values p = 0.3 or p = 1.7, the normalized intensities have the same form; in p = 0.5 or p = 1.5, the normalized intensities also have the same form; and in p = 0.7 or p = 1.3 the normalized intensities have the same form, too, but when 1 < p ≤ 2, the spot size of the Mainardi beam rotates compared to that of the p < 1. When p < 1 and q = 3, the spot size of the Mainardi beam in the FrFT system is similar to that of the Mainardi beam in the FFT system.

2.0

1.8

1.6

1.4

1.2

-8 -6 -4 -2 0 2   4 6 8

(a)

-8 -6 -4 -2 0 2   4 6 8

(d)

(e)

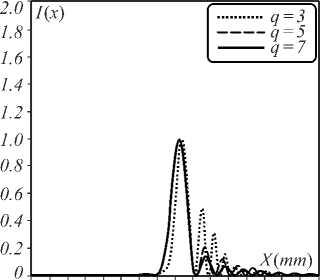
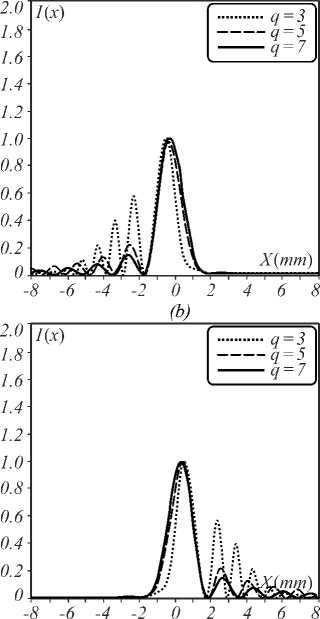
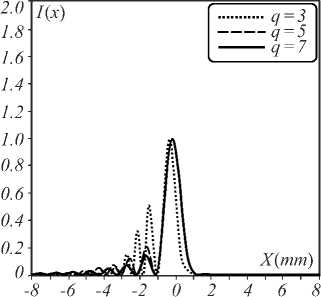
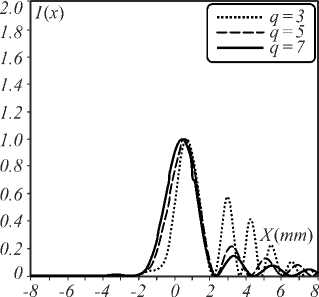
Fig. 4. Normalized intensity at q = 3 (dot line), q = 5 (thin line), and q = 7 (thick line) for (a) p = 0.3, (b) p = 0.5, (c) p = 0.7, (d) p = 1.3, (e) p = 1.5, and ( f ) p = 1.7

(f)

Figure 4 shows the normalized intensities in the x -di-rection of a Mainardi beam with a different q in the FrFT system for a = 0.05, x 0 = y 0 = 1 mm, q =3, 5, and 7. If p < 1, the spot beam size in the x -direction decreases with an increase in the power of the FrFT. For 1 <  p <2, the spot beam size in the x -direction increases with an increasing power of FrFT.

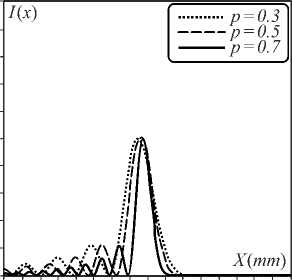
Figure 5 shows the normalized intensities in the x-di-rection of a Mainardi beam with different q in the FrFT system for a = 0.05, x0= y0= 1 mm, p = 0.3, 0.5, and 0.7. The effective beam size in the x-direction increases with an increase in the rational order of Mittag – Leffler function.

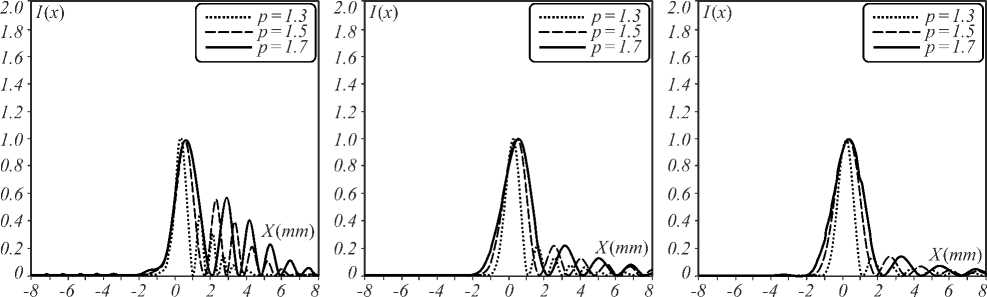
Figure 6 shows the normalized intensities in the x -direction of a Mainardi beam with different q in the FrFT system for a = 0.05, x 0 = y 0 = 1 mm, p = 1.3, 1.5, and 1.7. The effective beam size in the x -direction increases with an increase in the rational order of the Mittag – Leffler function.

(a)

-8 -6 -4 -2 0 2

(b)

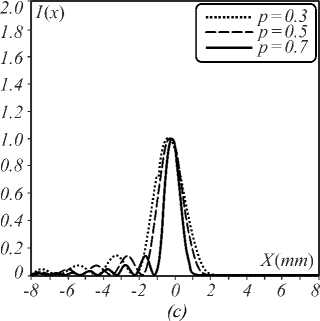
Fig. 5. Normalized intensity for p=0.3 (dot line), 0.5 (thin line), and 0.7 (thick line); (a) q = 3, (b) q = 5, (c) q = 7

(a)                                                       (b)                                                       (c)

Fig. 6. Normalized intensity for p=1.3 (dot line), 1.5 (thin line), and 1.7 (thick line); (a) q = 3, (b) q = 5, (c) q = 7

Conclusion

The analytical formulas of a Mainardi beam passing from the FFT and the FrFT systems calculate by using generalized Fresnel and Collin integrals. The obtained formula is a very powerful tool to describe propagation of a Mainardi beam through the FFT and the FrFT systems. The behavior of the Mainardi beam is similar to an Airy beam in the specific case in which the of Mainardi beam q have values 3, 5, and 7. We derived an analytical expression of a Mainardi beam passing through an FrFT system. We graphically illustrated the normalized intensity distribution of a Mainardi beam in the FrFT system, and we discussed the influences of the different q and p , on the normalized intensity distribution and characteristics of the beam. Powers of the FrFT affects spot size of a Mainardi beam, and controls the orientation of the Mainardi beam spot. When p ≤ 1, the effective beam size decreases with an increasing value of p , when 1 <  p ≤ 2 the effective beam size increases with an increasing value of p. The rational order of the Mittag – Leffler function influences the number of lateral side lobes of a Mainardi beam in the FrFT system. With an increase in the value of q , the main peak expands and height of the other peaks decrease. Therefore, the power of the FrFT ( p ) and the rational order of the Mittag – Leffler function ( q ) control the characteristics of a Mainardi beam such as the effective beam size, number, width, height, and orientation of the beam spots.