Study the One-bit Hard Combination Scheme on Cognitive Radio Users

As the demand for wireless communications increases, the spectrum scarcity has been become a major issue for service providers to deploy new services or enhance the capacity of existing applications. Recently, cognitive radio has been under active consideration to deal with conflict between the spectrum demand and inefficient spectrum utilization [1, 2]. Cognitive radio (CR) is a promising technique to improve the spectral efficiency of the wireless networks [3].Cognitive users need to detect the presence of licensed users in frequency band to be utilized. The use of a spectrum sensing technique enables to detect spectral holes and opportunistically use underutilized frequency bands. A number of single user spectrum sensing methods have been proposed [4, 5]. The use of a matched filter can provide optimum performance with prior knowledge on the primary user [4]. Cyclostationary feature detection can detect the signal in very low interference to noise power ratio (INR) condition, but it still requires some prior knowledge on the primary user [4]. Energy detection is simple to implement, but it may suffer from the presence of fading or shadowing [5]. Without prior knowledge on the primary user, the sensing performance of a single user spectrum sensing method may significantly deteriorate in deep fading environments [5]. To overcome this problem, the use of cooperative spectrum sensing has been proposed to achieve so-called multi-user diversity (MUD) gain [6-8]. As one of the most important components of CR, spectrum sensing enables the secondary users to adapt to the environment by detecting the spectrum holes without causing interference to the primary network. Cooperative spectrum sensing has been proposed as a solution to combat the multipath fading or shadowing effects [9-11]. Information from the cooperative secondary users is combined in the fusion center to make the final decision. Traditional one-bit hard decision for cooperative spectrum sensing has been investigated in [12-14], in which secondary users exchange only one-bit decisions rather than the sensing statistics. Soft combination in cooperative spectrum sensing has been proposed in [15-16], which outperforms one bit hard decision. However, the soft combination scheme requires much more overhead, e.g. the perfect channel state information between the primary users and secondary users are required for the maximum ratio combination (MRC). Double threshold energy detection has been studied [17]. Li Jiajun et al. proposed the weighted one bit hard combination scheme for cooperative spectrum sensing. Here, we have studied one-bit hard combination scheme for different number of cognitive radio users.

This paper is organized as follows: Section II describes different types of spectrum techniques. Section III provides data fusion technique. Section IV explains the system model under consideration is described. Section V discussed one-bit hard combination scheme. Section VI describes simulation result and discussion. And finally conclusion is drawn in section VII.

• II.    Spectrum Sensing Technique

Spectrum sensing methods for a cognitive radio system can be listed as follows.

• A.    Matched Filter Detection

The optimal way for any signal detection is a matched filter [18], since it maximizes received signal-to-noise ratio. However, a matched filter effectively requires demodulation of a primary user signal. This means that cognitive radio has a priori knowledge of primary user signal at both PHY and MAC layers, e.g. modulation type and order, pulse shaping, packet format. Such information might be pre-stored in CR memory, but the cumbersome part is that for demodulation it has to achieve coherency with primary user signal by performing timing and carrier synchronization, even channel equalization. This is still possible since most primary users have pilots, preambles, synchronization words or spreading codes that can be used for coherent detection. For examples: TV signal has narrowband pilot for audio and video carriers; CDMA systems have dedicated spreading codes for pilot and synchronization channels; OFDM packets have preambles for packet acquisition. The main advantage of matched filter is that due to coherency it requires less time to achieve high processing gain since only O(1/SNR) samples are needed to meet a given probability of detection constraint [19]. However, a significant drawback of a matched filter is that a cognitive radio would need a dedicated receiver for every primary user class.

• B.    Energy Detection

One approach to simplify matched filtering approach is to perform non-coherent detection through energy detection. This sub-optimal technique has been extensively used in radiometry. An energy detector can be implemented similar to spectrum analyzer by averaging frequency bins of a Fast Fourier Transform (FFT) [21]. Processing gain is proportional to FFT size N and observation/averaging time T. Increasing N improves frequency resolution which helps narrowband signal detection. Also, longer averaging time reduces the noise power thus improves SNR. However, due to non-coherent processing O (1/SNR2) samples are required to meet a probability of detection constraint [19]. There are several drawbacks of energy detectors that might diminish their simplicity in implementation. First, a threshold used for primary user detection is highly susceptible to unknown or changing noise levels. Even if the threshold would be set adaptively, presence of any in-band interference would confuse the energy detector. Furthermore, in frequency selective fading it is not clear how to set the threshold with respect to channel notches. Second, energy detector does not differentiate between modulated signals, noise and interference. Since, it cannot recognize the interference, it cannot benefit from adaptive signal processing for canceling the interferer. Furthermore, spectrum policy for using the band is constrained only to primary users, so a cognitive user should treat noise and other secondary users differently. Lastly, an energy detector does not work for spread spectrum signals: direct sequence and frequency hopping signals, for which more sophisticated signal processing algorithms, need to be devised. In general, we could increase detector robustness by looking into a primary signal footprint such as modulation type, data rate, or other signal feature.

• C.    Cyclostationary Feature Detection

Modulated signals are in general coupled with sine wave carriers, pulse trains, repeating spreading, hoping sequences, or cyclic prefixes which result in built-in periodicity. Even though the data is a stationary random process, these modulated signals are characterized as cyclostationary , since their statistics, mean and autocorrelation, exhibit periodicity. This periodicity is typically introduced intentionally in the signal format so that a receiver can exploit it for: parameter estimation such as carrier phase, pulse timing, or direction of arrival. This can then be used for detection of a random signal with a particular modulation type in a background of noise and other modulated signals. Common analysis of stationary random signals is based on autocorrelation function and power spectral density. On the other hand, cyclostationary signals exhibit correlation between widely separated spectral components due to spectral redundancy caused by periodicity [20].

• D.    Covariance Detection

This method determines if a primary user is present from the covariance matrix of the received signal, it uses the property that the off diagonal elements of the covariance matrix is non-zero when a primary user is present and zero otherwise.

• E.    Wavelet Detection

The spectrum of interest is decomposed as a train of consecutive frequency sub bands, wavelet transform is used to detect the irregularities in these bands (PSD is relatively smooth within the sub bands and possess irregularities at the edges between two neighboring sub bands). Wavelet transform carries information about the locations of these frequencies and the PSD of the sub bands. Vacant frequency bands are obtained by detecting the singularities of the PSD of the signal observed, by taking the wavelet transform of its PSD.

F. Cooperative Sensing

Cooperation is proposed as a solution to problems that arise in spectrum sensing due to noise uncertainty, fading, and shadowing. Cooperative sensing decreases the probabilities of miss-detection and false alarm considerably. In addition, cooperation can solve hidden primary user problem and it can decrease sensing time. In this technique, the cognitive radio users are populated in the range of primary transmitter to perform its individual signal detection using some detection methods and determine the reliability of its own detection results. We adopt OR rule of hard decision fusion method for this evaluation. Where, users send a binary local decision to data fusion center.

CR.-™1 >

CR-usal

CF.-uss- >

CR.-us«4 >

CR*usan ^

Data Fusion Center

Figure 2: Data fusion center.

HY OR Нй

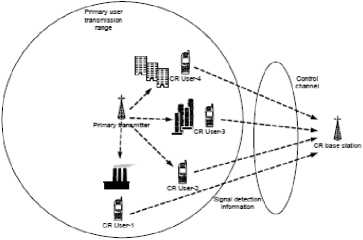
Figure 1: Cooperative signal detection model

As described in Figure 2, information of local signal observation from all cognitive users transmits to data fusion center. They forward 1-bit local detection to avoid communication overhead when CR users increased. Then, the final decision is performed whether signal is present ( H^ ) or absent ( H_o ) by regarding to decision rule. With a hard decision counting rule, the fusion center implements an n –out-of- M rule that decides on the signal present hypothesis whenever at least n out of the M local decisions indicate H . Assuming uncorrelated decisions, the probability of detection at the fusion center is given by [23]:

Pd =z

M, f M A

n V

k J

P d ,? ( i - P d , i Y - -

Figure 1 shows system model of cooperative signal detection where only one cognitive radio user could be able to detect the primary signal. The other cognitive radio users are not able to distinguish existence of the primary signal by fading and shadowing effect. The users are populated in the range of primary transmitter. Under this condition, it is expected that it can improve the signal detection probability. Collaboration among cognitive radio users is theoretically more accurate and convenient.

III. Data Fusion

In cooperative sensing, data fusion is a process of combining local sensing data for hypothesis testing, which is also an element of cooperative sensing in [22]. In hard combination scheme CR users make a local decision and transmit the one bit decision for hard combining. In order to realize the cooperative detection among CR users, the spectrum sensing and signal detection information over individual users should be sent to a fusion center for further process and the fusion center makes the final decision whether primary user signal is present or absent.

Where, P is the probability of detection node. In OR rule, if any one of the local decisions sent to the decision maker is a logical one (i.e., any one of the cognitive radio user decides that the signal of interest is present), the final decision made by the decision maker is one (i.e., decision maker decides that the signal of interest is present). Cooperative detection performance with this fusion rule can be evaluated by setting n =1 in equation (1).

P d , OR = 1 - ( 1 - P di ^ (2)

IV. System Model

The energy detector consists of a square law device followed by a finite time integrator (fig.3). The output of the integrator at any time is the energy of the input to the squaring device over the interval T in the past. The noise pre-filter serves to limit the noise bandwidth; the noise at the input to the squaring device has a bandlimited, flat spectral density in [23].

The binary hypothesis test for spectrum sensing at the nth time instant is formulated as [8]:

Ho : r ( n ) = w( n)

H_x : r ( n ) = x ( n ) + w ( n )

Where r ( n ) is the signal to be detected, x ( n ) is the primary signal with power CT_X 2 , and w ( n ) is the complex additive white Gaussian noise (AWGN) with ²

zero-mean and variance G_n .

Squari ng

Integrat

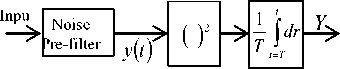
t = T

Figure 3: Energy Detection

t

Suppose there are N secondary users to perform cooperative spectrum sensing. As shown in Fig 4, two thresholds ( 2 , 2 ) are designed for one-bit hard combination of the proposed cooperative spectrum sensing, which divides the whole range of the decision statistic of the local spectrum sensing into three regions.

Without loss of generality, it is assumed that all the 2 powers of the local noise are the same and O n is normalized to be 1.

H and H denote the hypotheses corresponding to the absence and presence of the primary signal respectively. The local decision statistic is given by

Energy ( y )

M s = £l r ( n )Г                     (3

n = 1

Where, M is the number of samples. When there is only noise present,

Ж Region 2,	® 2 = 1
Region 1,	^ = 1
Region 0,	^ = 0

Figure 4: Cooperative spectrums sensing with two thresholds

M s 0 = XI w( n )|                      (4)

n = 1

Then the probability of false alarm can be expressed as [25-30]

The following weights are adopted in our scheme (У_о = 0 , ^ , < U₂ = 1 . In the fusion center, if the energy value falls into the corresponding region, it will be judged as "1", no information or "0". And the decision rule adopted is given

P f = P ( S 0 >  2 ) =

Г" ² 1 2T

Where Γ (⋅, ⋅) is the incomplete gamma function, Γ (⋅) is the gamma function and λ is the final threshold of the local detector to decide whether there is a primary user present. When there is primary signal present,

M s 1 = Xl x ( n ) + w( n f

n = 1

The probability of detection can be expressed as [26-32]

H

D =

N + N to, >  1

.

otherwise

P d = P ( s 1 >  2 ) =

™  7 =     = .

Where, /     ^,2

2on signal to noise ratio (SNR),

Ox denotes the signal

to

X

Q m ( a , b ) = j x ( x / a ) ^{m - 1} e

,— ₍ x ² + a 2 )/₂ . i m — 1 ( ax ) _dx

Where N is the number of local detectors the energies of which are greater than 2 and less than 2 , N 2 is the number of local detectors the energies of which are greater than 2 . Obviously, ^ should be more than 1/ N and less than 1. Let Q be the probability that one or more observation local energy values are greater than 2 and Q^ be the probability that more than N = ^ 1/ ^ J observation local energy values are greater than 2 and less than 2 . Here, ^ x J is the largest integer that is no more than x. We have from [21]

Q, 2 = 1 - P ( N 2 = 0| Я 0 ) = 1 - ( 1 - P f 2 ) N (10)

N

Q , , = P ( N 2 = OIH 0 ) . X P ( N 1 = j\H 0 )

J = N 1

N ^j

= ( 1 — P 2 ) N - Z | N ( P ,1 — P f 2 ) .б — P f 1 + P f 2 ) " - j          ⁽¹¹⁾

j = N , 1 ^j 7

is the generalized Marcum’s Q function and I denotes the modified Bessel function of the first kind.

Where P is the probability that the local energy value is greater than 2 and according to (4)

• V. One bit Hard Combination Scheme

  P fn = P ( S 0 >  A , ) =

  
  

  rf M ,   )

  I 2   2 J

  M

  
  
  
  
  
  

  We have

  
  

  A , = 2Г

  
  

  ^^^^s

  
  

  ■^{1 f} M p r| I 2 ^, P fn ¹ I

  
  

  M

  
  
  
  
  
  
  
  

  Г ¹ (, ) denotes the inverse of the incomplete gamma function. Then the probability of false alarm in the fusion center can be expressed as

  
  

  One Bit Hard Combination Scheme with Different CR users under AWGN

  =100

  =50

  =25

  =10

  Cognitive Radio User N Cognitive Radio User N

  Cognitive Radio User N Cognitive Radio User N

  0.9

  0.8

  0.7

  0.6

  0.5

  0.4

  0.3

  0.2

  0.1

  

  0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

  Probability of False alarm (Pfa)

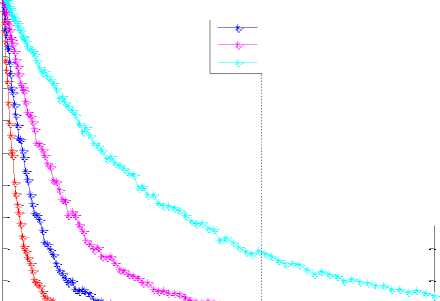
  Figure 5: One bit hard combination scheme versus conventional scheme with 10 user

  
  

  Q f = Q f 1 + Q f 2

  
  
  
  

  Suppose all the channels between the primary user and secondary users are independent identically distributed. The probability of detection in the fusion center can be expressed as in [21]

  
  

  Q d = 1 - ( 1 - P d 2 ) N + ( 1 - P d 2 ) N

  
  

  ^N

  Z N ( P d 1 - P d 2 ) j . ( 1 - P d 1 + P d 2 ) N ^- j       (15)

  j = N 1 V j J

  Where P is the probability that the local energy value is greater than A when there is primary present according to (6) and (7).

  VI. Simulation Result

  Simulation was done on MATLAB version R2011a under AWGN channel. We use complementary receiver characteristics (ROC) analysis for the signal detection theory to study the performance of one-bit hard combination scheme of cooperative spectrum sensing for different number of cognitive Radio   users.

  Complementary ROC has been widely used in the signal detection theory due to the fact that it is an ideal technique to quantify the tradeoff between the probability of detection and the probability of false alarm. The following simulation was done by taking time bandwidth factor u=TW=1000, primary user transmitting signal’s samples = 2000 and probability of false alarm (Pfa) is used from 0.01 to 1 by increasing 0.01, where 100 Pfa is used.

  
  

  Figure 5 shows complementary ROC of conventional OR rule and 1-bit OR rule in the hard combination scheme. Where 10 CR users and SNR=15dB were taken. It shows that the probability of missed detection is decreasing for both conventional hard combination and 1-bit hard combination scheme with OR rule correspondingly with increasing the probability of false alarm. It also shows that probability of missed detection in 1-bit hard combination scheme is reduced significantly than the conventional hard combination scheme although same CR user is used. 1-bit hard combination scheme has much better performance than conventional one-bit scheme.

  
  

  one-bit Combination scheme with Convensional OR rule with 10 user

  

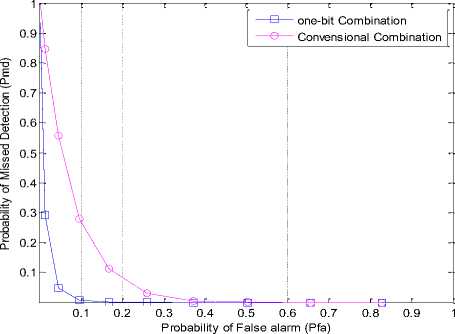
  Figure 6: One bit hard combination for different number CR users

  
  

  Figure 6 shows one bit hard combination scheme for different number of cognitive radio users. It is considered that the probability of missed detection versus probability of false alarm under AWGN channel with the complementary ROC of cooperative spectrum sensing with OR rule & different CR. The single to noise ratio was taken SNR=15dB.This simulation is tested by taking cognitive radio user N=10, 25, 50 and 100. Simulation result shows that with the increasing the probability of false alarm from 0.01 to 1, the missed detection is

  
  

decreasing. It also shows that probability of missed detection is decreasing when the CR user increases. When we take CR user 100 then missed detection probability is decreased than the CR user 10. So cooperation with more number of CR users in one-bit hard combination scheme, spectrum sensing is evaluated better performance.

• VII. Conclusions

Cognitive radio improves the utilization efficiency of the radio spectrum. Cooperative communications can play a key role in the development of CR networks. Simulation result demonstrated that the probability of missed detection is decreasing for both conventional hard combination and 1-bit hard combination scheme with OR rule correspondingly with increasing the probability of false alarm. It is shown that 1-bit scheme has much better performance than the conventional hard combination scheme. We saw that the probability of missed detection is decreased on increasing users.