Studying static stability of a model rocket

A flying rocket model is driven by a model rocket engine (MRE) and rises into the air without aerodynamic lift of the supporting surfaces (like an airplane). At the same time, the model rocket has a rescue system for its safe return to the ground. In rocket modeling, unguided rocket models are used rising to height of 150–250 m, provided their static stability is maintained during the flight.

A single-stage rocket model (Fig. 1) consists of conical 1 and transitional 2 parts of the fairing, the body of the rocket model 3 and fins - stabilizers 5.

Equipment of the rocket model: rocket engine 10, rescue system parachute 8, wad 9 and two guide rings.

The conical and cylindrical parts of the fairing are made of drawing paper. The workpiece is wound on a mandrel 4 and glued. The conical part of the fairing is made in a similar way. It should be noted that the diameter of the adapter has to be slightly smaller than the diameter of the case so that it can be freely put on and taken off. This ensures free ejection parachute rescue system.

Model rocket stabilizers moving the center of pressure closer to the tail of the rocket are four plates cut out of durable cardboard 1–2 mm thick.

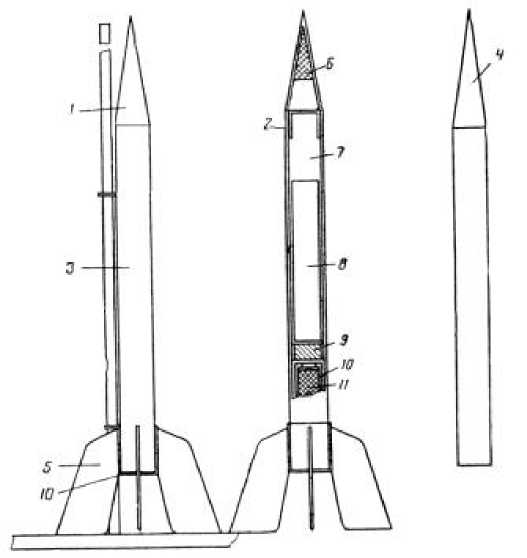
Рис. 1. Модель одноступенчатой ракеты:

1 – конусная часть головного обтекателя; 2 – переходник головного обтекателя;

3 – корпус модели ракеты; 4 – оправка; 5 – стабилизатор; 6 – полезный груз; 7 – стропы парашюта; 8 – парашют; 9 – пыж; 10 – микро-РДТТ; 11 – пороховая шашка микро РДТТ

• Fig. 1. Model of a single-stage rocket:

• 1    – conical part of the head fairing; 2 – head fairing adapter; 3 – rocket model body;

• 4    – mandrel; 5 – stabilizer; 6 – payload; 7 – parachute lines; 8 – parachute; 9 – wad;

10 – micro-SPRE; 11 – powder checker micro solid propellant rocket engine

Three forces have got an impact on a rocket in flight: engine thrust (R), aerodynamic drag (P), and gravity (G) (Fig. 2). The thrust force of the engine is directed along the longitudinal axis of the model; gravity acts vertically downward and is applied at the center of gravity (c. g.); the aerodynamic force is opposite to the oncoming flow and is applied at the center of pressure (c. p).The center of pressure is the point of application of the resultant of all aerodynamic forces to the rocket body [1–5].

When designing flying models of rockets, one of the complex tasks is to ensure the static stability of a rocket in flight along a given trajectory [6–9]. Stability refers to the ability of a model to return to an equilibrium position disturbed by external forces (wind, model asymmetry, others). In this case, the model should be stabilized due to the angle between the longitudinal axis of the model and the direction of flight (velocity vector). The condition to ensure the static stability of the rocket model is the location of its center of gravity ahead of the center of pressure. In this case, when the angle of attack is not equal to zero, the aerodynamic forces will create a stabilizing moment, which will return the model to a zero angle of attack [10; 11].

Fig. 2 demonstrates two cases of the behavior of a rocket model during its movement along a vertical trajectory. The angle of attack is zero; the axis of the model coincides with the direction of flight. Under ideal conditions (in the absence of external interference), such a trajectory is maintained throughout the flight. In reality, it is almost impossible to reach. External forces (wind, unstable engine thrust) introduce errors into the flight path due to the angle of attack is not equal to zero. If the model is statically stable (Fig. 2, a), it will return to zero angle of attack. An unstable rocket (Fig. 2, b) will further increase the angle of attack and deviate more from the original vertical trajectory.

Analyzing the existing methods to ensure the static stability of a model rocket

One of the most common ways to ensure the static stability of a rocket model is aerodynamic. It consists of installing special surfaces - stabilizers - on the rocket body.

We could consider the conditions of aerodynamic stability in details. It depends on the relative position of the center of gravity (c. g.) and the center of pressure (c. p.) (Fig. 3).

If c. g. is located in front of c. p (Fig. 3, a), when the angle of attack appears, the aerodynamic forces will create a stabilizing moment, which will return the model to its

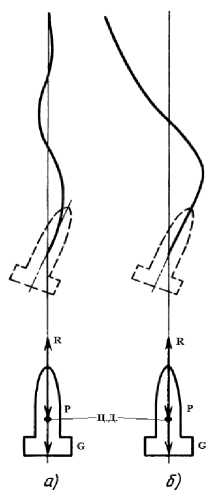
Рис. 2. Траектория полета модели ракеты: а – устойчивый полет;

б – неустойчивый полет

Fig. 2. Flight trajectory of the rocket model: a – stable flight; b – unstable flight

original state with a zero angle of attack. This model will be statically stable. The further displaced c.

g. relative to c. p. (counting from the head), the greater the margin of static stability the rocket model has got.

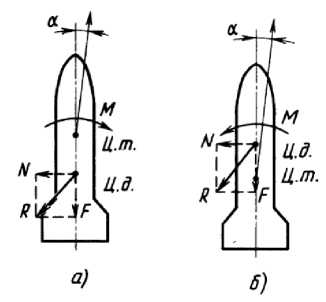
Рис. 3. Влияние взаимного расположения центра тяжести (ц. т.) и центра давления (ц. д.) на устойчивость модели в полете: а – модель устойчива; б – модель неустойчива

Fig. 3. Influence of the relative position of the center of gravity (c.g.) and the center of pressure (c. p.) on the stability of the model in flight: a – the model is stable; b – the model is unstable

If c. g. of the model is located behind c. p. (Fig. 3, b), thus, the aerodynamic forces arising as a result of a change in the angle of attack under the action of perturbing external forces will create a destabilizing moment that will increase this angle. This model will be unstable.

The ratio of the distance from c. g. to c. p. to the length of the rocket (at the origin at the head of the rocket) is called the static stability margin. For models with stabilizers, it should be 10-20%.

In practice, for model rockets, the center of pressure is shifted as close as possible to the engine compartment by increasing the total area of the stabilizers and installing them as far as possible from the head. In this case, the center of gravity is shifted to the head fairing due to the installation of an additional payload in the head part. The calculation of the static stability of a rocket, as a rule, is not specially carried out. Either traditional rocket models are used, which have already confirmed their static stability, or static stability is provided by test launches in the process of designing an experimental model.

Methods for calculating the static stability of a model rocket

The condition ensuring the static stability of the rocket model is the location of its center of gravity ahead of the center of pressure. s a rule, reference books on the strength of materials or calculation programs (SolidWorks, Ansys) are used to determine the geometric and mass characteristics of a structure [12]. However, the center of gravity of a model rocket can be easily determined by balancing it on the edge of a thin ruler. There are several techniques to find the center of pressure. As a rule, they are divided into calculated and practical ones [13–15].

Calculation method to determine the center of pressure

Approximate determination of the center of pressure according to the model drawing (on a flat figure)

The perturbations acting on the rocket model in flight are not great. The angle of deflection of the rocket changes slightly, as a rule, up to 15–20°. At low angles of attack, the position of c. p. deviates from the calculated. But when designing, it is possible to use an approximate method to determine the center of pressure in a symmetrical flow (at a zero angle of attack α = 0). The position of c. p. in this case will correspond to the position of the center of gravity of the flat figure of the model.

We could divide the model into a number of simple figures and find the coordinates of the total static moment (Fig. 4).

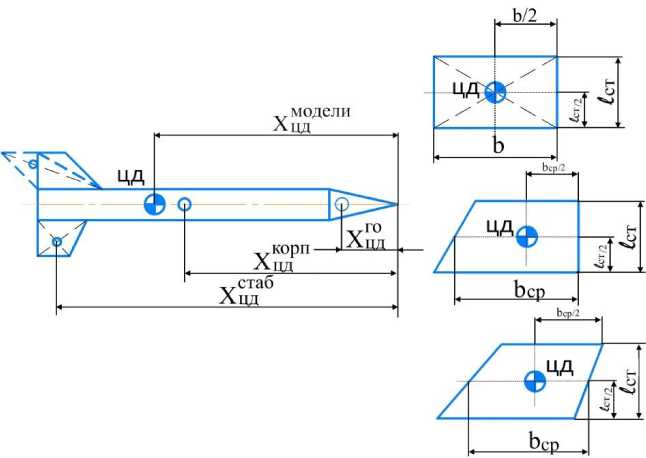
Рис. 4. Центр тяжести и центр давления модели и ее части

Fig.4. Center of gravity and center of pressure of the model and its parts го    го      корп    корп     стаб    стаб

X мдд = —цдцд— ,

where S ^го - fairing projection area; S ^корп - model body projection area; S ^стаб - projection area of all stabilizers; S ^мод - sum of all areas; X ^го - ordinate of c. p. of fairing; X ^корп - ordinate of c. p. of body model; X ^стаб - ordinate of c. p. of stabilizers.

If X ^мод - X ^мод = С is a positive number, this means that the model will be stable, where C is the stability margin of the rocket model. The more C, the more stable the flight is.

To increase the stability margin C , it is necessary to increase the area of the stabilizers or change their location to a more “rear” one (to shift the position of the c. p. closer to the tail compartment). To ensure a more anterior location of c. g., it is possible to increase the mass of the head fairing.

Graphical method to determine the center of pressure of a rocket model

The position of the center of pressure depends on the elongation of the body of the model

λ= корпуса . For a rocket model with a cylindrical body without fin and a conical (or closer to a cone) dмиделя nose fairing, the position c. p. on the model axis can be found from the graph (Fig. 5). Knowing the position of c. g. and c. p. of the unfinned rocket body, we could set the stability margin С (С = 30, С = 20, С = 10) and according to the graph we find the coefficient of influence of the stabilizers proposed by the authors, knowing this, we can calculate the area of one stabilizer fin for the 4-stabilizer model (Fig. 6) :

S ст = 0,8 ⋅ К ст ⋅ d м ² ид. .

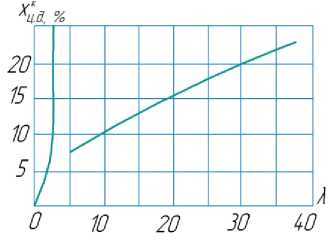
Рис. 5. График зависимости положения центра давления корпуса без стабилизаторов от его удлинения

Fig. 5. Graph of the dependence of the position of the center of pressure of the body without stabilizers on its elongation

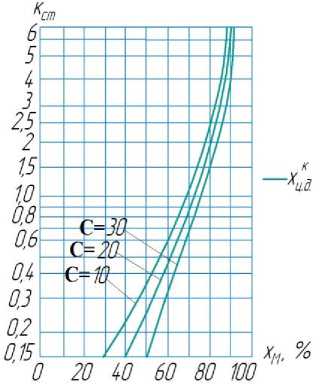
Рис. 6. График определения площади стабилизатора модели ракеты с четырьмя стабилизаторами

Fig. 6. Graph for determining the stabilizer area of a rocket model with four stabilizers

Analytical method to determine the position of the center of pressure according to the drawing model

A rocket model consists, as a rule, not only of cylindrical parts, but also of a number of conical ones. The graphic-analytical method does not take this into account, and a normal aerodynamic force acts on each of these parts. Knowing its magnitude and point of application, it is easy to find the total aerodynamic force R as the sum of individual forces and its coordinate Х у  _ Rro ■ Хго + R ■ Х1 - RK ■ Хк + R2 ■ Х2 + RCT ■ Хст

^Хц . д . =

R

where R _o, R , R , R₂ и R_CT - aerodynamic forces acting respectively on the head fairing, the first cylindrical part of the model, the conical, the second cylindrical part and the stabilizers of the model.

Since the aerodynamic force depends on the flight speed, it is better to determine not the forces themselves, but their dimensionless coefficients C . In this case, the formula can look like this:

Х ц.д.

C R

го X

го

+ C R

1 X ¹

—

C R kX^k

+ C R

; 2 2 X ²

+ C R

ст X ^ст

C R

while C_R = C_R + C_R — C_R, + C„ + C_R R     R го      R 1      R k      R 2      R ст

It is assumed in the calculation, a cylindrical body at small angles of attack does not create lift, thus, the aerodynamic force coefficient of a cylindrical body is close to zero. The calculation determines the aerodynamic performance for the head fairing, conical adapter and stabilizers. It should be taken into account that the presence of a cylindrical body affects the airflow near the root chords of the stabilizers.

Two types of head fairings are common: conical and ogive. For both types, the aerodynamic force coefficient is the same: C„  = 2.

R _го

For a conical head fairing, the center of pressure is located at a distance Х point, and for the ogive Х ц.д.

=---- L„ , where

2,15 ^го,

l_ro — fairing length.

=- R , its nasal

3 го

The conical adapter can increase or decrease the diameter of the model. The coefficient of aerodynamic force for the conical adapter is calculated by the formula

CRk = 2

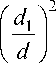
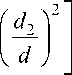
where d 1 — lower diameter of the truncated cone; d ₂ — upper diameter of the truncated cone; d — head fairing diameter.

For a tapering cone, this coefficient will turn out to be negative. This means the force R_к is directed against other forces and bodies differing in the aft part will have an unequal position of the center of pressure.

The position of the center of pressure of the cone is calculated by the formula

1 —

d ²

Xk = i_P + - kp ₃

1 +

d ₁

1—

d ₂ d

where l_p — distance from the nose point of the model to the cone; l_k — cone height.

Complex shape stabilizers can be represented as the sum of simple shape stabilizers, and their center of pressure can be determined from the average aerodynamic chord of the stabilizer fin. The aerodynamic force coefficient depends on the number of stabilizing surfaces. For a stabilizer with n surfaces, the aerodynamic force coefficient is calculated by the formula

C ^* R ст

N • ( l *т / d ) 2

2-1 I ¹ ср

Ко корн + ^Ь конц у

where l * - stabilizer fin span; l - span along the midline. The coefficient N depends on the number of stabilizers.

The aerodynamic interaction of the stabilizers and the body of the rocket model is taken into account by the coefficient

r

Kp = 1+ П ср where r – model aft radius.

Therefore, the coefficient of aerodynamic force for the entire aft part of the rocket model is equal to

*

Cr ⁼ Kn ’ Cr •

^R ст      ^{p   R} ст

The position of the center of pressure of the stabilizer depends on the shape of the stabilizer in plan and its location on the rocket body:

X k

= L +

^{A l} ( b корн ^{+ 2 Ь} конц ) ^Ь корн ^{+ Ь} конц

+ -

( ^Ь корн

k

^{+ Ь} конц

—

корн конц

> +b корн    конц у

where L - distance from the nose point of the model to the root chord of the stabilizers; A l - the distance between the beginning of the root and end chords of the stabilizer.

A practical method to determine the center of pressure

The first method. From plywood, cardboard or other sheet material, a figure is cut out along the contour of the rocket model and c. g. is found for this flat figure. This point will be the required c. p. of the model [2] (Fig. 7). For a real model rocket, made according to the presented contour, the true position of c. g. is determined due to the weight of the head, the mass of the engine, the rescue system, others. The static stability margin of the rocket is also determined by the formula X М^д — X ММд = С .

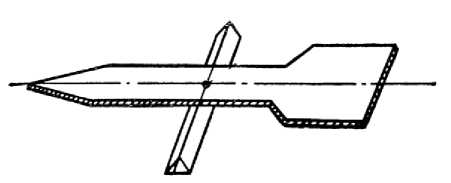
Рис. 7. Практический метод определения ц. д. плоской фигуры модели ракеты

Fig. 7. A practical method for determining c. p. a for flat figure model of a rocket

The second method – is a test of a rocket for stability using a wind tunnel. For this, the model is fully equipped: they put the engine, rescue system, wads, and other equipment. Further, the rocket is placed in the air stream towards the movement. The most uniform flow is created in a wind tunnel, the speed of which is at least 20–30 km/h. We could shift the rocket with a finger about 10º from the downstream position. If the model returns to its original position, then the static stability of the rocket is ensured (Fig. 8).

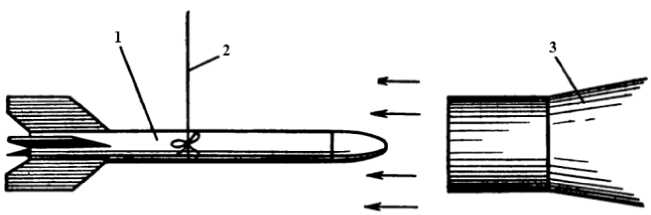
Рис. 8. Испытания модельной ракеты в потоке воздуха, выходящего из сопла аэродинамической трубы:

1 – модельная ракета; 2 – нить; 3 – аэродинамическая труба

Fig. 8. Tests of a Model Rocket in the Air Flow Out of the Wind Tunnel Nozzle: 1 – model rocket; 2 – thread; 3 – wind tunnel

In flight, as the fuel burns out in the engine, the position of c. g. of a model also changes. Almost all models has got the engine in the tail (stern) section. When the fuel burns, the mass of the rocket will decrease, and c. g. will move closer to the head, thereby, increasing the static stability of the model.

There are several ways to correct the stability of a model rocket. One of them is the displacement of c. p. to the stern by increasing the area of the stabilizers and their location. However, this is almost impossible to do on a finished rocket. Therefore, it is necessary to take into account possible options in advance (during its design): expand the aft part, choose the lower placement of stabilizers (behind the engine nozzle cut), increase the payload mass in the head fairing.

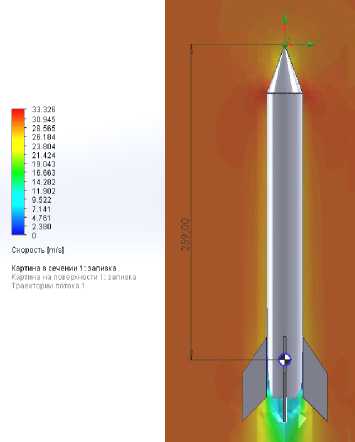
Рис. 9. Продувка модели ракеты с трапециевидными стабилизаторами в программе SolidWorks Flow Simulation

Fig.9. Purge model of a rocket with trapezoidal stabilizers in SolidWorks Flow Simulation

Comparison of methods for determining c. p. of a model rocket and determination of error

To determine the error of the described methods, we use three single-stage rockets with different types of stabilizers (Fig. 4)

We could note that the graphical method determines the area of the stabilizers with a known center of gravity of the rocket and the margin of static stability of the model.

Therefore, to find the position of c. p. we could use the opposite way, knowing the area of the stabilizers and c. p. of the unfinned body, we find the coefficient of influence of the stabilizers К _ст and the true position of c. p. of models. We could put these values into the table.

For practical definition of c. p. of a model rocket by blowing, we use the SolidWorks Flow Simulation program (Fig. 9).

Error in determining the center of pressure of a rocket model for stabilizers of various types

Ь/2 ^К^з^ , ь	Method to determine c. p.	Coordinate of c. p, mm	Absolute error, mm	Relative error, %
Calculated	On «flat figure»	177	45	15,52
	Graphical	252–258	30–36	10–12
	Analytical	223	1	0,34
Practical	On «flat figure»	178	44	15,17
	Blowing	222	–	–
/цд®
Calculated	On «flat figure»	173	46	15,86
	Graphical	249–252	30–33	10–11
	Analytical	220	1	0,34
Practical	On «flat figure»	173	46	15,86
	Blowing	219	–	–
Z__ /Г!
Calculated	On «flat figure»	177	82	28,28
	Graphical	243–249	16–10	6–3
	Analytical	259	0	0,00
Practical	On «flat figure»	179	80	27,59
	Blowing	259	–	–

Conclusion

Determining the center of pressure on a flat figure is the simplest and most reliable technique. It is advisable to use it for demonstration rockets with an allowable misalignment error of 15% or more. Analytical methods are appropriate for designing sports models of rockets with high flight requirements, for example, for international competitions, record flights.

The proposed technique to ensure the static stability of a model rocket makes it possible to simplify the design process of both demonstration and sports models for risk-free demonstration launches.