Subcarrier and Power Allocation in OFDM-based Cognitive Radio Systems

Published Online November 2010 in MECS

With the rapid development of wireless communications technology, radio spectrum resource is increasingly scarce. Cognitive radio (CR) [1] is a popular technology which can dynamically access to the vacant radio spectrum resource, effectively solve the problem of resources shortage, and increase the frequency spectrum efficiency.

Orthogonal Frequency Division Multiple (OFDM) technology [2] has been considered as an appropriate modulation candidate for CR system. In OFDM system, the frequency band is divided into a large number of small bands called subcarriers that use specific frequencies so as to be completely orthogonal to each other, which can not only reduce the mutual interference between the subcarriers, but also improve the spectral efficiency.

In the cognitive radio network, both CR user and PU exist in side-by-side bands, so mutual interference is the limiting factor for the performance of both systems. Therefore, both the total interference introduced to the PU band and the total power allocated to the CR users should

Corresponding Author: Longxiang Yang.

This work is supported by the Natural Science Foundation of China(61071090), 973 project(2007CB310607) of China, National be taken into account during the resource allocation to ensure that all users can be effectively coexistence.

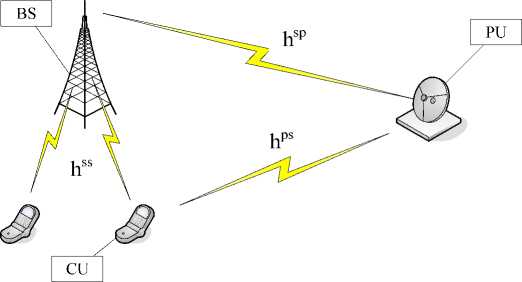
Figure 1. Distribution of primary and CR users in the spatial domain

The classical water filling algorithm [3] for allocating power to subcarriers in OFDM systems is not suitable in the CR context, because it does not take into consideration of the protection of primary users operating in nearby bands. The basic idea in the water filling algorithm is to assign more power to subcarriers that experience higher channel gain, while assigning little or no power to subcarriers suffering from low channel gain. However, in the context of CR, a set of subcarriers experiencing favorable channel quality may be adjacent to a primary user band. Thus, if the water filling algorithm is employed, those subcarriers will typically be assigned higher power levels, which in turn will cause severe interference to the adjacent primary users.

Considering that joint subcarrier and power allocation in OFDM system is a complex problem, thus, the problem is usually simplified by separating subcarrier allocation and power allocation. In [4], power, time slots and subcarriers are jointly optimized by two separate optimal algorithms in three steps while keep fairness among users and maximization of total capacity. However, the existence of primary user has not been taken into considered. In [5], two novel algorithms are presented for subcarrier and power allocation in OFDMA-based CR networks, which are constant power subcarrier allocation and heuristic joint subcarrier and power allocation respectively. Both of them are aiming at maximizing the sum capacity while maintaining the interference power introduced in the primary network band below a predefined threshold. In [6], an optimal and two suboptimal power loading algorithms

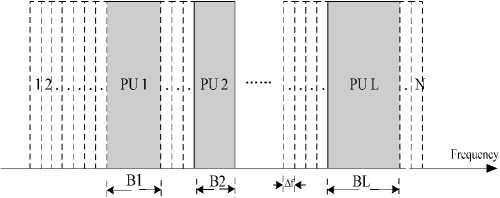
Figure 2. Distribution of primary and CR users in the frequency domain

for an OFDM-based cognitive radio system are investigated while keeping the interference introduced to the primary user within a tolerable range only.

This paper investigates the subcarrier and power allocation problem in CR systems, where primary and CR users co-exist in adjacent bands, while keeping the total interference introduced to the PU band below a certain threshold and the total power allocated to the CR users under a constraint. In the first part, according to the different purposes of the resource allocation, several suboptimal subcarrier allocation algorithms are investigated. First, we investigate Max-Rate subcarrier allocation algorithm (MaxR-SAA) which can achieve maximum transmit rate of the CR system. In this algorithm, interference introduced to the PU band is kept under the constraint, but it is still very high. Besides, fairness among all the second users (SU) is not taken into consideration. Then, focusing on the fact that the less interference introduced to the PU band, the better the PU can work; we proposed a Min-Interference subcarrier allocation algorithm (MinI-SAA). Further, aiming at achieving fairness among all the SUs, we propose a subcarrier allocation algorithm, which is termed as FairRate subcarrier allocation algorithm (FairR-SAA). In the second part, for a given subcarrier allocation three suboptimal power allocation algorithms which have less complexity are proposed and compared to the optimal power allocation algorithm [7].

The organization of this paper is as follows. Section II describes the system model and the problem is formulated. In Section III, several suboptimal subcarrier allocation algorithms are investigated, which are termed as MaxRate, Min-Interference and Fair-Rate subcarrier allocation algorithm. The algorithm for optimal and suboptimal power allocation for the given subcarriers is presented in Section IV. Numerical results are given in Section V, and finally, Section VI concludes the paper.

• II.    SYSTEM MODEL AND PROBLEM FORMULATION

We consider the side-by-side CR radio access model, as shown in Fig.2. The total frequency bandwidth is assumed to be B, on which bandwidth B1 , B2,..., BL , are occupied by the PU(s) 1,2,...,L, respectively, and are sensed by the CR system consisting of K users. The unoccupied band sensed by the CR system for possible transmission is located on both sides of L primary user bands, and the PU can be located anywhere of the frequency bands. It is assumed that the available bandwidth for CR transmission is divided into N subcarriers, each of which has a bandwidth ofЛf Hz, as shown in Fig.2.

It is assumed that channel gain hkss,n , hks,pn, hkp,sn can be perfectly known at the CR user’s transmitter, where hks,sn denotes the channel gain between the kth CR user transmitter and receiver, hks,pn denotes the channel gain between the kth CR user transmitter and the PU receiver and ps denotes the k,n channel gain between PU transmitter and the kth CR user receiver, as shown in Fig.1. Then, the transmission rate for the kth CR user for the nth subcarrier can be expressed as [6], hks,sn2Pk,n

Rk.n — log 2(1 +--—— ст2 +У LJ(1 1

Z—i 1 —1 k , „

)

（ 1 ）

where Pk, n is the transmission power allocated to the k‘h CR user for the nth subcarrier, ст2 is the AWGN variance and VL J(1' is the interference introduced to i । k,„ kth CR user’s nth subcarrier by all the PU bands.

Under the influence of the side lobe of the spectrum, electromagnetic signal may experience some radiation and leak of spectrum. Since both CR user and PU exist in side-by-side bands, mutual interference is the limiting factor for the performance of both systems, which is determined by the transmission power and the spectrum distance between the CR user and the primary user.

• A.    Interference introduced by CR user’s signal

Under the situation of an ideal Nyquist pulse, the power density spectrum of the n ^th subcarrier which is allocated to the k ^th CR user can be written as [9]

ф к , n — P k,n T s I      ^fT s I                    ( 2 )

I nfTs J where Ts is the symbol duration. The interference introduced by the nth subcarrier to the lth PU band is the integration of the power density spectrum of the nth subcarrier across the lth PU band, and can be written as sin nfTs J

I df ( 3 )

where d nl denotes the spectrum distance between the n ^th subcarrier and the l ^th PU band. Then, Equation (3) can be written as

I ^{( 1} ' I k , n

—        p ( ¹ )

^{— P k} , . * F

（ 4 ）

• ( 1 )        ^SP    T f dni + Bi / 21 sin ⁿJ^Ts I

where F k , . ^— h k„ I T s f _dm_ _{/S( /} 2 ^ j । d^f , which is denoted as the interference factor between the k ^th CR user for the n ^th subcarrier and the l ^th PU band.

• B.    Interference introduced by primary user’s signal

The power density spectrum of the primary user signal after the M-fast Fourier transform (FFT) processing can be expressed as [9]

E { I n ( w ) }

1 _f - к         । sini w - v) M Г2 | /_cn

—1— фри(ejw)  \ )\  dv 5) 2nM n        ^ sin(w-v)/2 J where w represents the frequency normalized to the sampling frequency and фри(ejw) is the power density spectrum of the PU signal. Then, the interference introduced by the lth PU to the kth CR user for the nth subcarrier can be written as

J (‘) = | h d2 I d ”* ^{+ A} f ^/2 E^wW      (6)

k , ”     |^k , ”| ^d n* -Д f /2 I \ /J

• C.    Problem formulation

The optimization problem of resource allocation is to maximize the total capacity of CR users while keeping the total interference introduced to the PU band below a certain threshold and the total power allocated to the CR users under a constraint.

It can be written mathematically as follows

KN                 hkssn 2 Pk, n max X X Pk■ ” log 2(1 + ———tv)

/ .. , ■ . .^^'              ._2           *

k =1 ” =1                ° ⁺ x * _{= 1} ^Jk, ”

subject to xx p k,n P k,n F *” < I t* , l=1,2,_L

KN xx Pk ■ ” < Pt , Pk, n > 0 k=1 - =1

K x pk, ” = 1 , pk, n = {0,1} k=1

where Pt denotes the total power budget which is allocated to the CR users, I * ) denotes the interference threshold of the * ^th primary user, and p k , n =1 means that the n ^th subcarrier is allocated to the k ^th CR user. Besides, it is assumed that one particular subcarrier can be allocated to only one user while one user can occupy multi-subcarrier.

This paper first investigates the subcarrier allocation problem in a sub-optimal fashion. Then for a given subcarrier allocation, three suboptimal power allocation algorithms are proposed and compared to the optimal power allocation algorithm. In the next section, we first present the algorithms for sub-optimal subcarrier allocation.

Ш . SUBCARRIER ALLOCATION

Subcarrier allocation, the base of the bit and power allocation, is to decide two problems. One is how many subcarriers should be allocated to each user; the other is how to allocate them. In this section, we propose three subcarrier allocation algorithms which are Max-Rate subcarrier allocation algorithm (MaxR-SAA), Min

Interference subcarrier allocation algorithm (MinI-SAA) and Fair-Rate subcarrier allocation algorithm (FairR-SAA), separately.

As [10] is said, as long as the subcarriers are allocated properly, the smooth power density spectrum will not cause the debase of the throughput of the system. Therefore, to predigest the analysis, it is assumed that equal power is allocated to every subcarrier, according to [7]. For all the interference thresholds and power constraint to satisfy, we allocate equal power as follows

Pt

N ^,

P eq = min ‘

J ( 1 )              И²)                   TL^L )

th                  th                       th

KN , KN ,..., KN xx F n xx Fa xx F l k = 1 - = 1 k = 1 - = 1               k = 1 n = 1

Considering that a single user be scheduled on each subcarrier, therefore, the problem of subcarrier allocation is essentially to choose a user for each subcarrier. We define the set of all subcarriers as A = { 1,2,..., N } , and Q k denotes the set of subcarriers assigned to the CR user k. Since each subcarrier can be only allocated to one CR user, we can draw that

Q. I Q, = 0 V k * j , and U Q. = A .

^{k 1}                               k =1 ^k

• A.    MaxR-SAA

In CR systems, to improve the spectrum efficiency, CR users can sense and access the vacant spectrum. Max-Rate subcarrier allocation algorithm aims at achieve maximum transmit rate of the CR system, while keeping the total interference introduced to the PU band below a certain threshold and the total power allocated to the CR users under a constraint. Therefore, the MaxR-SAA problem in OFDM-based CR systems can be formulated as

K                      K                      hks,sn Pk, n max x x Rk,- = max x x log2(1 +      ' l ,*)) (9)

. . k=1 neQk          , . k=1 neQk             C + / J, k=1,...,k                        k=1,..., к                            v Д1}=1V k, n subject to ]T x Pk, ”F**< I*), l=1,2,^,L k=1 n eQk x x Pk,” < Pt, Pk, ” > 0

k=1 n eQk where Qk can be obtained by following steps:

• 1)    Initialization:

• a)    R k , n = 0 for k = 1,..., K , n = 1,..., N ;

• b)    Q k = 0 for k = 1,..., K ;

• 2)    for n = 1,..., N

^h k^s , ^sn ²

• a)    find CR user k = arg max---^!---——, for

’                             ° ²₊y ^lj ( * ) ^,

I=1 k^n k = 1,...,K ;

• b)    allocate the found subcarrier n to the CR user k , Q k = Q k U n ;

• c)    update R _{k , n} according to (1).

• B.    MinI-SAA

Since in a CR network, where the CR users and the PUs exist in side by side spectrum, we should insure that the PU can work without interruption. So the interference introduced to the PU band should be as little as possible. Therefore, the MinI-SAA problem in OFDM-based CR systems can be formulated as

LK        LK m-" 111 ik". =m" HI f£* P-    («я k=1 к 1=1 k=1 nefik           k=1 к 1=1 k=1 nefik

Z Z Pk,. < Pt , Pk,. > 0 k=1 n efik where fik can be obtained by following steps:

• 1)    Initialization:

• a)    R k , . = 0 for k = 1,..., K , n = 1,..., N ;

• b)    fi k = 0 for k = 1,..., K ;

• 2)    for n = 1,..., N

• a)    find CR user k = arg min V L F, ■ ^{1 1} , for 1 =1 ’n.

k = 1,..., K ;

• b)    allocate the found subcarrier n to the CR user k , fi k = fi k U n ;

• c)    update R _{k , n} according to (1).

• C.    FairR-SAA

Aiming at achieving fairness among all the SUs, first, we propose a statistic as follows,

S k . n

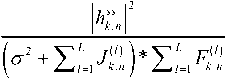
where both the mutual interference between the CR user and PU and the capacity of the CR system are taken into account. Therefore, the FairR-SAA subcarrier allocation algorithm can be described as follows:

• 1)    Initialization:

• a)    R k , . = 0 for k = 1,..., K , n = 1,..., N ;

• b)    fi k = 0 for k = 1,..., K ;

• c)    A = { 1,2,..., N } ;

• 2)    for k = 1,..., K

• a)    find subcarrier n = arg max S k. , for n e A ;

• b)    allocate the found subcarrier n to the CR user k , fi k = fi k U n , A = A - { n } ;

• c)    update R _{k , n} according to (1).

• 3)    while A + 0

• a)    find CR user k = arg min ^ R k . n ;

n efi k

• b)    for the found CR user k , find subcarrier n = arg max S _kn , for n e A ;

• c)    allocate the found subcarrier n to the CR user k , fi k = fi k U n , A = A - { n } ;

• d)    update R _{k , n} according to (1).

In this section, each subcarrier allocation algorithm has its own advantage. For example, the MaxR-SAA can achieve the maximum transmit rate, the MinI-SAA introduces the least interference to the PU band and the FairR-SAA can almost achieve fairness among all the SUs . During the next section, we use the Fair-Rate subcarrier allocation algorithm, which allocates subcarriers to CR users in a manner that not only the capacity of CR users is increased but also the interference introduced to the PU band is decreased.

W . POWER ALLOCATION

As the subcarrier allocation is given, we should allocate power to each subcarrier in order to maximize the total capacity of CR users while keeping the total interference introduced to the PU below a certain threshold and the total power allocated to the CR users under a constraint. In this section we investigate the optimal power allocation algorithm and propose three suboptimal power allocation algorithms named distance-based step power allocation algorithm, interference-based step power allocation algorithm and modified equal power allocation algorithm, which have less complexity.

• A.    Optimal power allocation

For the given subcarrier allocation algorithm, the optimal power allocation problem is formulated as

K max zz log2(1 +

Pk ’ n k=1 n efik hkss,n2Pk,n

²+ y^L Л¹¹ i =1 k , ⁿ

)

K subj ect to z z Pk, nFkln < Ih1 k=1 nefik

K

Z Z P k ’ n <  Pt , P k ■ n >  0

k =1 n efi k

By introducing the Lagrange multiplier and the Karush-Kuhn-Tucker conditions, we can get the optimal solution [7] as

z iiU h k^s , ^sn ²

n e Q k ,

（ 15 ）

N

X PB < Pt ^ p = n =1

Pt

N

X(1/ Kn)

n =1

（ 21 ）

where wk, n =--------------, and в and Xi are Lagrange в + X 1=1 XFl)

multipliers which can be determined according to the subjection conditions (13) and (14).

• B.    Step power allocation

Scheme A ( Distance-based ): In this scheme, the step size is fixed and is equal to the power level of the subcarrier which is nearest to the primary user band. Hence, the power allocated to the n ^th subcarrier can be written as

P )A = p * n                     (16)

where p is the step size. Then, according to the interference threshold of the primary user, p can be expressed as

N

X K n * P⁴ = I th ^ p = ------ (17)

• ⁿ =¹                    X K n * n

n =1

L where Kn = X F^ denotes the sum interference i=1

introduced by the n ^th subcarrier allocated to the k ^th CR user to all the primary users.

Then, according to the constraint on the total power budget allocated to the CR users, the step size p can be expressed as

N P A <  Pt ^ p =              ⁽¹⁸⁾

n=1                  X n n = 1

Use the lesser solution calculated by (17) and (18) as the final step size, and substitute it to (15) to obtain the value of P _n ^A .

Scheme B ( Interference-based ): In this scheme, the step size of the ladder is inversely proportional to K n . Hence, the power allocated to the n ^th subcarrier can be written as

P = P / Kn where p is the step size. Then, according to the interference threshold of the primary user, the step size p can be written as

• УК* * P B = I th ^ p = I ^th            ( 20 )

^X n         N

Then, according to the constraint on the total power budget allocated to the CR users, the step size p can be written as

Use the lesser solution calculated by (20) and (21) as the final step size, and substitute it to (19) to obtain the value of P _n ^B .

• C.    Modified equal power allocation

For the sake of fairness, we can allocate equal power to each subcarrier. During the subcarrier allocation in section III, where we allocate equal power to all subcarriers, we consider that total interference introduced

KN to the lth PU is XX Г*1) , however, after the subcarrier k=1 n=1

allocation, each CR user can only occupy part of the subcarriers. So we need to modify the total interference as K

X X Fk'n . Therefore, the power which is equally k=1 neQk allocated to the subcarriers should be written as

D_T         J ^{( 1 )}                /( ^{2 )}                     TL^L )

P^t       I th              I th                  I th

, _K , _K ,..., _K

^N XX F^ XX F k 2 ¹   XX F k⁽L )

k = 1 n eQ k         k = 1 n eQ k             k = 1 n eQ k

Ⅴ . NUMERICAL RESULTS

For the numerical results presented in this section, we use the values of Ts, ^л f and B to be 4gs , 0.3125MHz and 5MHz respectively. AWGN variance is assumed to be 10-6. The channel is assumed to be Rayleigh fading with an average channel power gain of 1dB. Further, we assume that there are one primary user and two CR users. The primary user has a frequency bandwith of 1MHz, and a central frequency of 1.5MHz, whose interference threshold is2 x 10 -6 W.

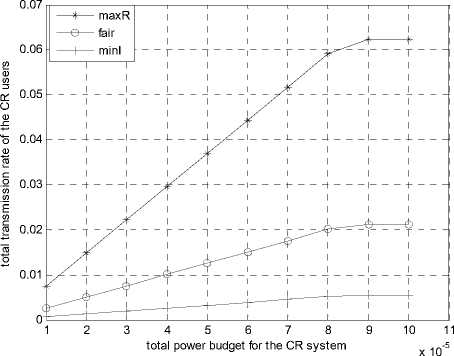
Figure 3. Total transmission rate of the CR users

Pt/10-4

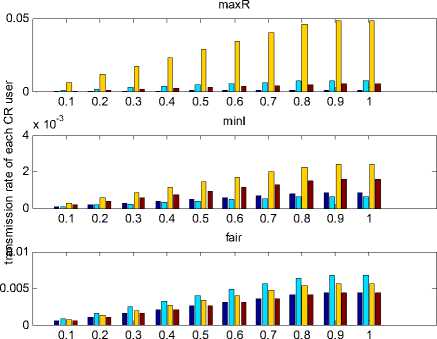
Figure 5. Transmission rate of each CR user

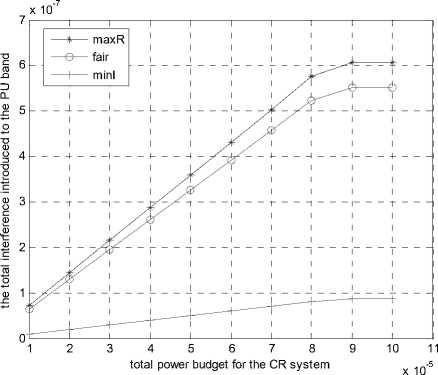
Figure 4. Total interference introduced to PU band

total power budget for the CR system

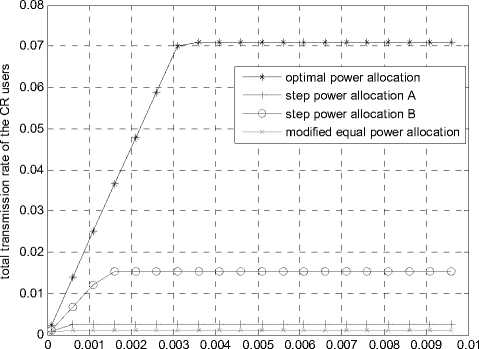
Figure 6. Total transmission rate of the CR users

Fig.3 shows the total transmission rate of the CR users versus the total power budget for the CR system, where as the total power budget increases, the total transmission rate of the CR users is increasing at first, and will come to be steady. Further, as we expect, the MaxR-SAA can achieve the highest transmission rate among the algorithms we have proposed, while the MinI-SAA achieves the lowest. However, as we can see from Fig.4, which shows the total interference introduced to the PU band versus the total power budget for the CR system, the MaxR-SAA caused higher interference to the PU band than the MinI-SAA, and obviously, the MinI-SAA caused least interference to the PU band.

What is more, the transmission rate of each CR user is observed in Fig. 5. We can draw that only the FairR-SAA can almost obtain fairness among all the CR users, which means that the transmission rate of each CR user can be almost the same. And from Fig.3 and Fig.4, we can draw that the FairR-SAA is a tradeoff between the MaxR-SAA and MinI-SAA at the aspect of the total transmission rate of the CR users and the total interference introduced to the PU band.

In Fig.7 and Fig.8, we can draw that all the algorithms in this paper can satisfy both the interference threshold and the power budget constraints. In Fig.8, we can see that the total transmitted power is equal to the prescribed power budget threshold when the power budget of the CR system is small. At this time, the algorithms are in the power-limit state. Then, as the power budget of CR system increases, the total transmission rate of the CR users is increasing. When the power budget reaches a certain value, as shown in Fig.7, the total interference introduced to the PU band will come up to the interference threshold, and the algorithms will enter into the interference-limit state. After the two states mentioned above, all the algorithms will come up to the maximum transmitted data rate and remain steady while the power budget increases.

Furthermore, we can see from Fig.7, for the given power budget of the CR system, the optimal scheme achieves the highest transmission rate for CR users and causes the least interference to PU band. Performance of the suboptimal power allocation algorithms which have less complexity is much worse than the optimal scheme. Besides, it is also obvious that the step power allocation algorithm B performs better than the step power allocation algorithm A, and offers the best performance among the suboptimal power allocation algorithms. Moreover, though the modified equal power allocation algorithm can achieve partly fairness among the CR users, it offers the worst performance.

Ж CONCLUSION

In this paper, we have investigated the subcarrier and power allocation problem in CR systems, where primary and CR users co-exist in adjacent bands, while keeping the total interference introduced to the PU band below a certain threshold and the total power allocated to the CR users under a constraint. First, according to the different purposes of the resource allocation, Max-Rate, MinInterference and Fair-Rate subcarrier allocation algorithms are investigated, separately. Further, for the given subcarrier allocation algorithm, three suboptimal power allocation algorithms which have less complexity are proposed

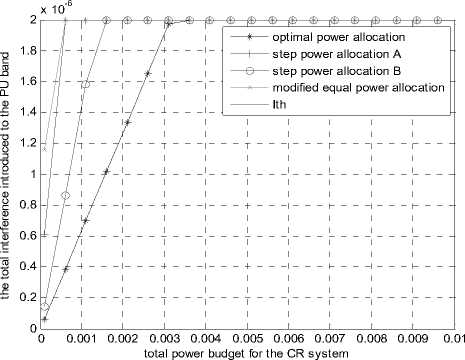
Figure 7. Total interference introduced to PU band

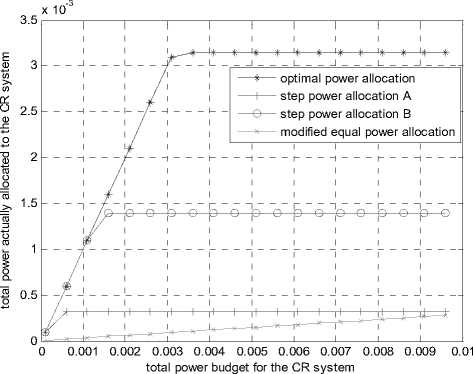
Figure 8. Total power actually allocated to CR system

Z. Shen, J. G. Andrews, and B. L. Evans, “ Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints”, in IEEE Trans. on Wireless Commun., vol. 4, No. 6, pp. 2726-2737, Nov. 2005.

Feng-Seng Chu, Kwang-Cheng Chen, “Radio Resource Allocation in OFDMA Cognitive Radio Systems” Personal, Indoor and Mobile Radio Communications, 2007. IEEE 18th International Symposium on Digital Object Identifier: 10.1109/PIMRC.2007.4394507, Page(s): 1 – 5,2007.

G. Bansal, Md. J. Hossain, and V. K. Bhargava, “ Optimal and suboptimal power allocation schemes for OFDMbased cognitive radio systems, ” in IEEE Trans. on Wireless Commun., vol. 7, No. 11, pp. 4710-4718, Nov. 2008.

G. Bansal, Md. J. Hossain, and V. K. Bhargava, “Subcarrier and power adaptation for multiuser OFDMbased cognitive radio systems”, Communications (NCC), 2010 National Conference on Digital Object Identifier: 10.1109/NCC.2010.5430230 Publication Year: 2010 , Page(s): 1 - 5

Lun Tang, Huan Wang, Qianbin Chen, Guangming Liu, “Subcarrier and power allocation for OFDM-based cognitive radio networks”, Communications Technology and Applications, 2009. ICCTA '09. IEEE International Conference on Digital Object Identifier: 10.1109/ICCOMTA.2009.5349158 Publication Year: 2009 , Page(s): 457 – 461

T.Weiss, J.Hillenbrand, A.Krohn, and F.K.Jondral, “Mutual interference in OFDM-based spectrum pooling systems,” in Proc. IEEE Vehicular Technol. Conf. (VTC’04), vol.4, pp.1873-1877, May 2004

RHEE W. CIOFFI J M. “Increase in capacity of multiuser OFDM system using dynamic subchannel allocation” [C]. IEEE.Proceedings of IEEE Internationsl Vehicular Technology conference. Tokyo; IEEE, 2000: 1085-1089.

and compared to the optimal power allocation algorithm. Simulation results have shown that all the algorithms in this paper can always maintain the interference threshold and power constraint and that among the subcarrier allocation algorithms we proposed, the MaxR-SAA can achieve the maximum transmit rate, the MinI-SAA introduces the least interference to the PU band and the FairR-SAA can almost achieve fairness among all the SUs. Furthermore, the step power allocation algorithm B offers the best performance among the suboptimal power allocation algorithms. Besides, when fairness is taken into account in the modified equal power allocation algorithm, it will cost the capacity of the CR system.