Субгармонический отклик третьего порядка для осциллятора Дуффинга, возмущенного гармоническим и случайным воздействием

Introduction. In this paper, we are concerned with the Duffing oscillator, which has been applied to model many mechanical systems and has attracted much attention as a typical nonlinear system. When the system is under only a harmonic excitation or random one, two popular tools used to study such a nonlinear system are the averaging method and equivalent linearization method, respectively. The former was originally given by Krylov and Bogolyubov [1] and then it was developed by Bogolyubov and Mitropolskiy [2-4] and was extended to systems under a random excitation with the works of Stratonovich [5], Khasminskii [6], and others, which were reviewed in survey paper by Mitropolskiy [3], Robert and Spanos [7] and Manohar [8]. The later, the stochastic equivalent linearization method, which has attracted many researchers due to its originality and capability for various applications in engineering, was first studies by Kazakov [9], who extended Krylov and Bogolyubov's linearization technique [1] of deterministic problems to random problems. This method was also reviewed in some books by Roberts and Spanos [10], and Socha [11]. Recently, some approaches to the stochastic linearization have been proposed in Refs. [12-14]. In [13-14], for example, Anh et al. have proposed a dual criterion of stochastic linearization method for single and multi-degree-of-freedom nonlinear systems under white noise random excitations. The authors showed that the accuracy of the mean-square response is significantly improved when the nonlinearity increases.

In a Duffing oscillator under periodic excitation, the phenomenon of subharmonic response has been known for years and has been described in many textbooks (see e.g. [15-18]) and works (see e.g. [19-21]). When the system is subjected to a combination of harmonic and random excitations, however, to the authors' knowledge, although the response of this oscillator has received a flurry of research effort for years (see e.g. [22-25]), there is no work on its subharmonic response. Thus, in this research, we present a technique to treat a one third order subharmonic response of a Duffing oscillator subjected to periodic and random excitations. The technique is a combination of the stochastic averaging method, the equivalent linearization method, and the technique of auxiliary function which yields the exact joint stationary probability den- sity function (PDF) for the equivalent linear system [4,26,27]. The approximate analytical solution of the Duffing system obtained by the proposed technique is validated by numerical simulation results, obtained by Monte-Carlo method.

1. Formulation problem. Let us consider Duffing oscillator under harmonic and random excitations of the form z+ 8 hz + 8уz3 + ® 2 z P cos Vt+ Vs^(t) ,                               (1)

where z (t ), z(t ), z(t ) are the displacement, velocity and acceleration of the system, respectively; 8 is a small positive parameter; h is the damping coefficient; У is the nonlinear stiffness coefficient; ю is the natural frequency of the corresponding linear system when 8 =0; P , V and О" are parameters; and function ь ( t ) is a Gaussian white noise process of unit intensity with the correlation function R = (^г) ⁼ E^(t)^(t + г)] = ОД , where 5(г) is the Dirac delta function, and notation E (.) denotes the mathematical expectation operator. It is supposed that the natural frequency (В is close to V /3 , i.e. parameters (В and V have the relation

2 V2

0) 2,

9, where А is a detuning parameter. We introduce a new variable x as follows

р x = z-Qcos vt ,Q =       .

(В 22

Using (3) Eq. (1) can be rewritten in the form

X + йэ 2X = 8^-/7(х -\Qsin\’ty^^x + Qcos 3           .(4)

Substituting (2) into Eq. (4) we obtain 2

+ 1 3J Х = 8.Р^Х,X,Г) +VeCT^(f),(5)

where

FkX,X,t^ = -\x - h[x -vQsinvt^-^(x + Qcos v03.

We seek the solution of Eq. (5) in the form of x = b cos-t + dsin-t , x = --^r sin +   cos-t,

3  33333

where b and d are slowly varying random processes satisfying an additional condition b cos       sin-t =0.(8)

Substituting (7) into Eq. (5) and then solving the resulting equation and Eq. (8) with respect to the derivatives b and d yield

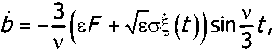
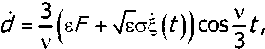
where, noting (6) and (7),

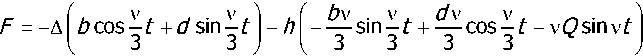
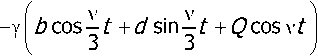
The pair of stochastic differential equations (9) can be simplified by using the stochastic averaging method [3-7]

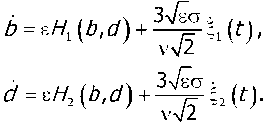
Here 11(f) and |₂(f) are independent white noises with unit intensity, and the drift coefficients H 1 ( b , d) and ₂ , are determined as follows

,         1 2 3 sin            ,       ,       1 2 3 cos             .(12)

1             20         3     3       2           20          33

Substituting(6), (7) into (12) yields the drift coefficients of the system (11)

6   92

• 1 ,                                                       2         32,

2        4         8

,          6     9                    9       3       2       22

• 2      428

The Fokker-Planck (FP) equation written for the stationary probability density function (PDF) W^b, d^ associated with the system (11) has the form

92     22

,,

1                           2                   42       22

Solution of (14) is still a difficult problem so far because functions ₁ , and ₂ , are nonlinear functions in , . To overcome this, the equivalent linearization method is employed. Following this method, the nonlinear functions ₁, ₂ are replaced by linear ones. Noting (13), we denote

• 1,        9      2        32,

• 2,        9        3        2        22

According to the stochastic equivalent linearization method the nonlinear functions (15) are replaced by

1    ,           11        1213

2    ,           21        2223

where linearization coefficients ,   1, 2;    1, 2, 3 are to be determined by an optimization criterion.

Thus, the functions ,   1,2 in (13) are replaced by linear functions uihavLh       6К +91Q2

1 (Ь ^,<У)- - ₂■ + л11            4       ^н л12 к + п13

24V )

6А +9iQ2     )    ( h ) , н2 {Ь, ^Н"    4-----+ п21        2■ + п 22 \d + т]23.

4V                2

According to the technique of auxiliary function with the constant auxiliary function taking the form (see [4,26,27] for details)

и 0

6А +9 •jQ ²

2V

+ П21 -п12

⁴v²       -h + т| 11 + п22

the corresponding FP equation to Eq. (14), where drift coefficients are linear functions (17), has the following exact solution

W(ь,d)    exp {-т1b2- т2d2+ т3 bd + т 4b + т5 d^ ,(19)

where C is a normalization constant and coefficients Ту ,/ = 1,5 are determined as follows

_ И h Y ,         х Г 6 А + 9 iQ 26А +9 iQ ²

т1            2■ + п 11 (-/7 +Г]11 + П 22)+ -     4------+ п21         2------+ п21 -п12

2     11                                42

,                                    6 А + 9 1Q 26А +9 1Q ²

2         (-А + П11 + T| 22 ) " 2 ■ + Т| 22                      НТ|21 -n12                 НТ|12,

22V4v

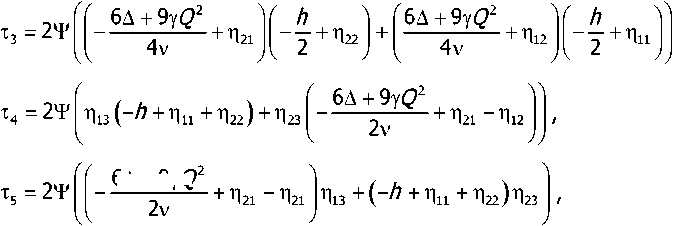
6A +9YV

,

where

2v2 (-^ + n11 + n22 )

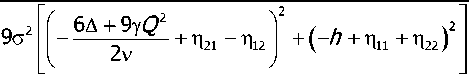
It is noted that the joint PDF l¥(/2, ^) determined by (19) has finite integral if coefficients i ₁ and i ₂ are positive. Therefore, the approximate stationary PDF of Eq. (14) is determined by (19) whose coefficients are given in (20). It is seen from (19) that random variables b and d are jointly Gaussian. Thus, from(19), one obtains

2T2T4+ T3T5          2T1T5+ T3T42

2 ,                               2 , b

^4T1^T2 "^T23              4 ^T1^T2 "^T3 ²

2I2

4T1T2 "T 23

2 2 T 1

^{d    4T}1^T2    2 ₃

,

4T1T23

where a ² and a ² are variance of b and d , respectively, and k_M is covariance of b and d . It is seen from (22) that necessary statistics of processes b and d can be computed algebraically based on coeffi-42

cients of joint PDF W^b , d) . Thus, the approximate solution (19) of Eq. (1) is completely determined when the linearization coefficients ^v ,/ = 1,2; j = 1, 2, 3 are found.

There are some criteria for determining the coefficients Лу [20]. In this work, we use the mean square error criterion which requires that the mean square of the following errors be minimum [10,11]. From (13), (15)-(17) we have the errors when using linearization method to be e, = Qi ^ ,d)-^1b + Ai2d + П/3),i =1,2.(23)

So, the mean square error criterion leads to

Eke.2) = ^(^,tf)-(n,1£ + n,2d + n, 3 )]2p min, / = 1,2; j = 1,2,3.(24)

From

——Eke2) = 0, / = 1,2;j =1,2,3,(25)

it follows that

E^bg1 kb,d^-El.b2)n11 - E (/%/) r|12 -^(#)n13 0, E\d g1 kb ,d^-Ekbd^11 -Ekd2)n12 -Ekd^13 0, E\g1 kb,d)] -FI6)y11 -Ekd^xy12 -n13

E\bg2 kb,d^-E^b2)n21 - E (Zk/)t|22 -^(#)n23 0, E\d g2 kb,d)}-Ekbd)y\21 -Ekd2)n22 -^(^)n23 0, El92 kb,d)] -F(*h21 -Ekd^xy22 -n230, where g1 kb , d) ,g2 kb , d) are given by (15). Using the fact that b and d are jointly Gaussian, all higher moments of b and d in (26) can be expressed in terms of the first and second moments of b and d by the following properties of a Gaussian random vector X = kx1,X2 ^ = kb, d^ [28]

f( Yⁿ⁺ 1 Y \F( Yⁿ\-E 2 F(Yⁿ~ 1

с                          + П<зу, EJ

e(x X" 1 2 \ = e(x\e(x" 1 2 \ + n.k„ .,E(X? 1 1 x^{n 2}               1 xⁿ 21/ =

1    2                           1    2         1      1        1       2         2      2        1    2      ,1,2.

Solving system (26) in Пу ,/ = 1,2; j = 1, 2, 3 with noting (27) gives

8 X                    x                 x                                  x           x                 /

Thus, Л у,/ = 1,2; i = 1, 2, 3 are determined from the closed system of eleven equations for eleven unknowns

^у ,/ = 1,2; j =1,2,3 ; Е^ , Е (^) , а 2 ,а 2 , ^bd , obtained by combining equations in (20), (22), and (28).

After being found by solving this closed system, the values of coefficients ^0 ,/ =1,2; j = 1,2,3 are to be substituted into (19) to obtain the approximate stationary PDF in b and d of Duffing equation (1).

From (7), the mean square response of Eq. (5) can be determined as follows

EV 2 (t^ = E^b2) cos2 3t^E^d2) sin2 3 t + E^bd) sin 3-t .(29)

Taking averaging with respect to time Eq. (29) gives

№2 «= 21 2   2 (f)X 3x 12 (^2)+^2 )) .(30)

From properties of a variance of a random variable [28], Eq. (30) can be rewritten as

(Ф 2 MJ), - 12 (^2(^)+ст2 *E2^ + O2) .

Substituting (22) into (31) and reducing the obtained result yield the time-averaging of mean square response to be

(f[* ² (0J)_f

224   352   215   342     12

2 4 1 2     23 2                 4 1 2

where T, ,/ = 1, 5 are given by (20). From (3), one obtains

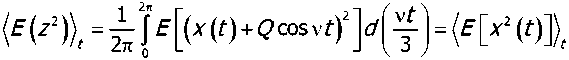
Q ²

2 24   35 ²    2 15   34 ²      1   2       ²

2( 4 T₁T₂- T 3² )24^T1^T2 "^T 2₃     2

Substituting (32) into (33) yields

This formula shows that the time-averaged mean square one third order subharmonic response of the system can be computed from the coefficients of the stationary PDF (19).

• 2.    Numerical results. In the numerical simulation, the parameters in system (1) are chosen as follows CD = 1 , V = 3.01 , 8 = 0.01, Y =1 , h =2 , P - 1 . The various values of the subharmonic response of Duffing

equation (1) are compared to the numerical simulation results versus the parameter а2 . The numerical simulation of the time- averaged mean square response kz2 is obtained by 10,000-realization Monte Carlo simulation with time t in the interval (900s, 1000s). The time-averaged mean square response ^v2 )^ of the Duffing oscillator, obtained by the system (22), (28) and (34), are compared to a numerical result. The response versus the parameter a2 is evaluated in Table 1 where the error is defined as

Err

x100% .

It is seen from Table 1 that the proposed technique gives a good prediction. Moreover, Fig. 1 portrays the variation of the mean square subharmonic responses 2 )) obtained by the present technique with the noise parameter (J2 compared to ones obtained by Monte-Carlo simulation. It is seen that the theoretical prediction and the simulations agree very well.

Table 1

The error between the simulation result and approximate values of the time-averaging of mean square response 2 versus the parameter 2      1,   3.01,    1,    2,   0.01,   1

2	2 \     / sim	2	Err %
0.1	0.0323	0.0331	2.48
0.5	0.1328	0.1350	1.69
1	0.2599	0.2626	1.03
2	0.4978	0.5136	3.18
3	0.7272	0.7607	4.61
4	0.9850	1.0074	2.28
5	1.2271	1.2545	2.23

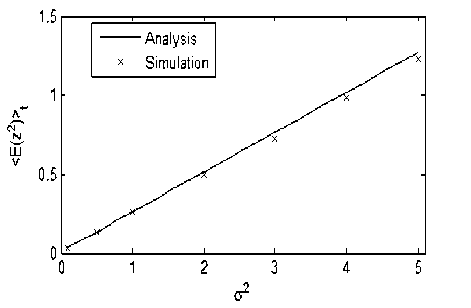
Fig. 1. The time-averaged mean square subharmonic response versus the parameter cr² (o = 1,v = 3.01, P= 1, h = 2, e =0.01,/ = 1)

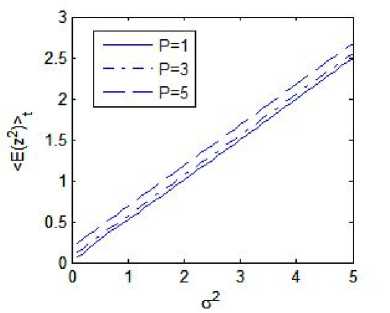
Fig. 2. Effects of cr² and P on the mean square subharmonic response, ® = 1,3 0 3.01,s = 0.01, h = 1,^ = 1

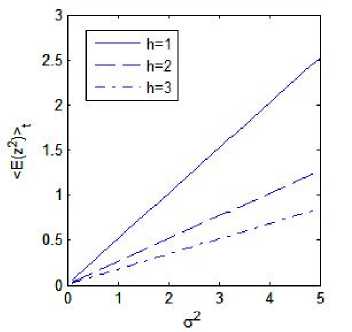
Fig. 3. Effects of СУ ² and h on the mean square subharmonic response, со = 1, V = 3.01, 8 = 0.01, P 1, у ⁼1

Next, we investigate the effects of the noise intensity СУ ² , external force amplitude P , and the damping term h on the one third order subharmonic response based on equations (22), (28) and (34). With initial values

(п11,П12,П13,П21 , П 22 , П 23 ) = (“ 1, 1,1,0, 1,1), and the input parameters СО = 1, V = 3.01, £ = 0.01, у = 1 , theoretical results are shown in Fig. 2 and Fig. 3. It can be observed that from Fig. 2 that the mean response amplitude increases when harmonic excitation increases. In Fig. 3, we can see that for given parameters 0) ,V,Р,8,Y the time-averaged mean square response decreases as the damping coefficient increases.

• 3.    Summary and conclusions. The averaging method and the equivalent linearization method are famous tools in studying nonlinear systems subjected to harmonic and random excitation, respectively. A combination of those methods will give a power tool to study complex systems. In this work, the subharmonic response of one third order of Duffing oscillator under a combination of harmonic and random excitations is investigated. The technique used in our research is a combination of the two famous methods mentioned above and the technique of auxiliary function to overcome the difficulty in solving the corresponding FP equation. The key steps of the technique are summarized as follows. First, the stochastic averaging of the equation (1) is carried out in Cartesian coordinates by the transformations (3) and (7). The drift coefficients of the averaged equations in the system (11) are polynomial forms in random variables which give an advantageous context to apply the equivalent linearization method. The linearization coefficients are determined by a closed system including the equations in (22), (28) and (34). The FP equation associated with the equivalent linearized system can be solved exactly by the technique of auxiliary function. The theoretical results are agreed well with numerical simulations.

It appears that the new approach gained through this study has a large potential and it will become helpful for other types of nonlinear systems.