Subspace based Expression Recognition Using Combinational Gabor based Feature Fusion

• I.    Introduction

  Facial expression recognition is a kind of cognitive nonverbal task used in various applications to understand the human internal feelings. Human drowsiness of vehicle driver can be recognized with suitable facial expression recognition approach. In medical field to understand the patient situation their facial expressions might be useful. Accuracy of human expression recognition depends on the situation of face image has taken. The mobile sciences, medical diagnosis, mind training, psychological studies, security based systems all have different views of the facial expressions. Plutchik emotional model presented in [1] illustrates the relationship between one to one emotions generated by different expressions. Ekman and Friesen [2] proposed Facial Action Coding System (FACS) for expression recognition during 1978. Ekman [2] was categorized the expressions based on distinct properties of faces as anger, happy, sad, surprise, disgust and fear. Main objective of this research work is to recognize the different

expressions efficiently by enhancing the Gabor filter magnitude and phase features by fusing the upper and lower face features geometrical features. The dimensionality of the feature dataset has been reduced by implementing different subspace methods by preserving the discriminative face features. The scope of this study is to introduce the novel approach for efficient facial expression recognition for limited area of face region. In this work various linear and non linear subspace methods have been tested with three databases. The dimensional reduction of fused feature dataset has been carried out by implementing subspace methods.

In this paper section II illustrates the related work. Section III delivers proposed feature level fusion. Section IV briefly overviews the subspace methods. Results and discussions are made in Section V. Conclusions are drawn in Section VI.

• II.    Related Work

  Peng et al. (2005) [3] worked on facial expression recognition and classification using minimum redundancy –maximum relevance method which has been based on mutual information to select the subset of features during reduction of features space. Bai et al. (2009) [4] they combined LBP features and Gabor features of face images. For efficient expression recognition they used weighted LBP Gabor complex features with linear discriminant analysis. Yu and Yang [5] have been used class discriminative based approach to recognize the face by discarding null space from between class matrix and diagonalized the within scatter matrix in order to solve the problem of singularity matrix. Xie et al. [6] presented Gabor based feature extraction by separating Gabor magnitude and phase parts separately. Phase part has been modified by introducing local Gabor exclusive OR patterns. They carried out expression recognition by reducing the high dimensional space by introducing block based Fisher linear discriminant analysis. In our work a novel approach for fusion of extracted features based on geometrical and appearance methods have been proposed. Geometrical eigen feature vectors have been generated for limited areas of face part.

According to several literatures it can be viewed as Linear Discriminant Analysis (LDA) method can be used for expression recognition for different databases. If number of expression data samples reduces then performance of LDA algorithm becomes fall down and scatter matrix also becomes singular. Hence it would be difficult to maintain larger variability between two classes. Optimization for the singularity matrix problems were noticed by Belhumeur et al. [7] and proposed a Fisherface method (FF), which uses old and more useful principal component analysis (PCA ) [15] based subspace projection strategy. Li et al. [8] did discriminant analysis based non parametric approach recognition. Spectral regression kernel discriminate analysis (SRKDA) have been proposed by Ming et al. [9], and suggested that SRKDA method can efficiently yields better solutions than ordinary dimensional reduced subspace learning approaches. Rahulamathavan et al [10] introduced facial expression recognition system with encrypted domain using linear Local Fisher discriminant analysis (LFDA). Author was tested JAFFE data base with the developed algorithm and achieved 94.37% recognition rates. Happy and Routray [11] worked on patch based strategy for different face appearances. For expression classification discriminative features were considered by further patches obtained from active patches. Feature extraction by Gabor filter with local binary pattern and dimensional reduction of high dimensional data concept is introduced by Abdulrahman et al. [47]. Liu et al. (2012) [48] has been carried out facial expression recognition based on the fusion of geometry features and texture features. Deng et al. [52] demonstrated about local Gabor based feature extraction with LDA and PCA projection. Zhen and Zilu [53] tested JAFFE database using fusion approach which was framed by Gabor filter and 70% of overall recognition accuracy has been achieved.

Linear and nonlinear subspace projection methods were directly implemented by some researchers on input image dataset to achieve feature extraction and dimension reduction. Different subspace methods were implemented on high dimensional feature dataset for dimensional reduction and compared the consequences of subspace methods [12]. George et al. [13] worked on facial expression recognition with SMS alert. Various state of art on facial expression recognition system was made by Bettadapura in [14]. One of the most popular and old subspace methods such as principal component analysis (PCA) [15-20] has been used in this work for projection of Fisher linear discrimiant subspace [38-42]. Struc and Pavesic [21] worked on Gabor filter based feature extraction by considering magnitude and phase parts separately for face recognition application. Both magnitude and phase feature vectors were projected by Fisher LDA algorithm. Linear Fisher Discriminant Analysis for face recognition has been demonstrated by Sugiyama et al. [51]. In our work linear and nonlinear discriminant based subspace methods have been utilized for reduction of high dimensional data to low dimensional data. Different scales and orientations of Gabor filter has been utilized for construction of high dimensional combinational based feature dataset. Zhaoyu Wang and Shangfei Wang (2011) [53] proposed a feature level fusion for efficient expression recognition for thermal and visible face images. Their approach improves the recognition accuracy of negative expressions. Thiago et al. [54] presented a feature level fusion by utilizing Gabor filter and Local Binary Pattern (LBP) for efficient recognition of expressions, they got 96.2% of expression recognition rate, their work does not support for dimensional reduction of high level feature dataset.

• III.    Proposed Frame Work

In this work total Gabor filter space has been divided in to two separate spaces such as Gabor filter magnitude space and phase feature space [21]. These two feature vectors have been fused with extracted geometrical feature vectors. In this section a novel approach for fusion of feature extraction have been proposed. Geometrical feature extraction has been carried out with a new concept of limited regions of the face which is compatible with textures features during the fusion of extracted features. Geometrical features are essential for expression recognition and classification. These features changes whenever the face region gets deformed with different movements in the muscles of the face. Region of interested areas have been selected from different face templates and some fiducial points were located on face image. Basic architecture of entire expression recognition system based extraction of both geometrical and holistically features supports efficient recognition and classification of expressions after subspace projection. Both geometric and holistic features are key elements for final expression recognition.

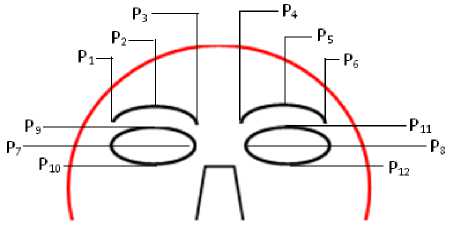
Fig.1. Locations of fiducial points on upper part of the face image

In this paper geometrical feature has been extracted which is related to AAM model feature extraction approach, points were marked on corner point of eyes, where the upper and lower eyelid meet called eye canthus.

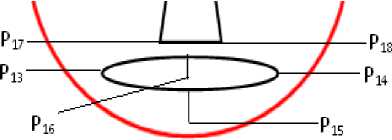
Fig.2. Locations of fiducial points on lower part of the face image

Pre marked points on upper face and lower face parts yields geometrical features, which supports texture information. Fig. 1 and Fig. 2 shows location of fiducial points on face. In this work 18 fiducial points has been located on face image and 16 dimensions eigen vectors has been computed as given in (4). In upper face part P 1 to P 12 points were marked by selecting eyes and eyebrows face templates as local points. In left eye brow P 1 , P 2 , P 3 points were marked and in right eye brow P₄, P₅, P₆ points were marked respectively as shown in Fig. 3. Some points like P₉ , P₁₀, P₁₁, P₁₂ are marked on upper and lower eyelids respectively on both the eyes. Corner points of eyes are P₇ and P₈. Variation of eye brow and eyelids movements makes the different values of eigen values. Points P 7 and P 8 are to be considered as inner canthi on reference points.

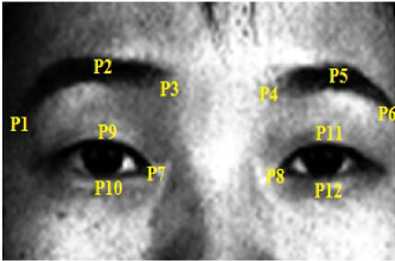
Fig.3. Upper part of the face and pre-marked fiducial points

In lower part of the face nose and mouth templates have been considered, two extreme ends of lip were marked by points P13 and P14 as shown in Fig. 4. Middle points of the lower and upper lip were marked as P15 and P16. Some of the expressions are exhibited based on compression and expansion of nostrils position. The magnitude of eigen vector and meaning of each geometry features are shown in Table 1. In this table, mi ( P1, . . . ,P18) is the abscissa of ith point and ni( P1, ....P18) is the ordinate of ith point ( a point where the pre-marking has been done).

Table 1. Eigen vectors of geometrical features

Magnitude of Eigen vector	Equivalent meaning			Magnitude of Eigen vector	Equivalent meaning
EG 1		nP - E		EG 9		nP 12 - P 11
EG 2		nP2 - E		EG 10		nP 13 - E
EG 3		n^ - E		EG 11		nP14 - E
EG 4		mP - mP		EG 12		nP 16 - E
EG 5		ПР4 - E		EG 13		nP 16 - ^P 15
EG 6		np5 - E		EG 14		mP 14 - P 13
EG 7		np6 - E		EG 15		nP 17 - E
EG 8		nP 10 - P 9		EG 16		nP 18 - E

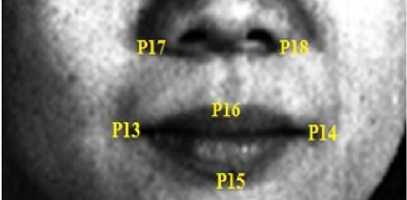
Fig.4. Lower part of the face and pre-marked fiducial points

E =

| mP^ - mP -y |

Where E is a reference value or base value is a constant in magnitude. Base E is the central point of the two inner canthi. In respect that the inner canthi (point P7 and P8) are constant in 18 feature points, these points are considered as the reference points, and then 16dimensional eigenvector {EG1, EG2, EG3 ....EG16} are obtained. During experiment validation {EG1, EG2, EG3 ....EG16} has been used as facial expression eigen value features feasibility analysis. For all the databases eigen feature based geometrical feature extraction procedure has been implemented. Geometrical Feature Eigen Vector (GFEV) is computed as follows.

GFEVupper =[EG1,EG 2, EG3......EG12 J

GFEVlower = \EG13’ EG14,.....EG16 J

The total dimension of geometrical feature vector (GFV) is 16 is given as

GFV = [EG1, EG2,.....EG16J

Magnitude part of the Gabor filter has been enhanced by combining Gabor filter magnitude feature vector with upper face part geometrical features. Similarly phase part of Gabor filter has been enhanced by combining Gabor filter with lower face part geometrical features. Gabor magnitude feature vector (GMFV) is fused with Upper face geometrical feature vector (GFEV_upper) and Combinational Gabor Magnitude Feature Vector (CGMFV) have been formed. Similarly Gabor phase feature vector (GPFV) is fused with lower face part geometrical    feature vector (GFEV lower )    and

Combinational Gabor Phase Feature Vector have been formed. Proposed expression recognition system using feature level fusion and discriminant based subspace methods presented in Fig. 5. Feature level fused dataset of both combinational Gabor magnitude and combinational Gabor phase has been projected using different linear and nonlinear subspace methods. Projected subspaces of both CGM and CGP were fused using score level fusion and Combinational Entire Gabor (CEG) subspace has been formed. This CEG subspace has been computed for both training dataset images and testing images respectively. Euclidean distance have been computed between final score matrix of both the train and testing CEG subspace. Based on the Euclidean distance metric expressions were recognized. All the expressions were classified using “Leave One Out “strategy of support vector machine classifier. Table 1 presents Eigen values of geometrical feature vectors for upper and lower face part.

structures of data by maximize the variance. It uses second order statistics by referring orthogonal space analysis. This method basically lies on eigenface concept. Consider a combinational Gabor dataset G, which consists of N measurements g^ (1 < i < N) in a high dimensional space R^m. This can also represented as

G - [ gV" g N ] ^e R m ^X N

.

The main scope of

Input face image dataset

Testing images

dimensional reduction strategy is to compute respective low dimensional space can be given

S - [ ^ 1 , .... ^ 2 ] e R d ^{x N}

.

Where d

the the by For

Face detection and pie-piocessmg

Face detection and pre-processing

Gabor maputude feature vector (GMFV)

Geometrical feature vector (GFV)

Gabor phase feature vector (GPFV)

Gabor magnitude feature vector (GMFV)

Geometrical feature vector (GFV)

Gabor phase feature vector (GPFV)

combinational Gabor PCA projection matrix can be represented as S=WTG. Where W is transformation matrix. The objective function of combinational entire Gabor PCA (CEGPCA) is given as

max N     2

W iS(gi - g)

Feature level fusion

Feature level fusion

Feature level fusion

Feature level fusion

1N g  Ni§ gi

Combinational Gabor magnitude feature vector (CGMFV)

Combinational Gabor phase feature vector (CGPFV)

Formation of combinational entire Gabor normalized low dimensional projected sibspace by matchiiig score leve 1 fusion

Combinational Gabor inaptitude feature vector (CGMFV)

Combinational Gabor phase feature vector (CGPFV)

Formation of combinational entire Gabor normalized low dimensional projected sib space by matchiiig score leve 1 fusion

Computation of similarity malm and Euclidean distance

Expression recognition and classification

Fig.5. Proposed feature level fusion and expression recognition system

• IV.    Dimension Reduction By Subspace Methods

Where g is the mean value of combinational Gabor feature dataset of G samples. FLDA algorithm was developed by Belhumeur et al. [7]. It surplus the performance of eigenfaces (PCA) approach, in some cases FLDA works well even if different illumination occurs with lower error rate. Also works well even if different facial expression takes place. FLDA maximizes the between-class scatter matrix variance and minimizes the within-class scatter matrix variance. FLDA finds vital role as a basic strategy in discriminant based approaches for expression recognition and classifications. When number of features in feature space becomes larger than the number of training samples, then within scatter matrix becomes more singular. Limitation of number of training samples causes this singularity problem. In this work high dimensional combinational Gabor dataset has been reduced by class discriminative subspace approaches by referring our earlier work mentioned in [12]. In FLDA between class matrix Sb can be given as

In this section brief overview of subspace methods have been discussed. Subspace methods finds vital role for dimensional reduction of higher dimensional data. Curse of dimensionality is a problem for subspace projection. Intermediate feature dimension reduction has been implemented on proposed feature level fused dataset for different values of dimensions of images with different values of Gabor filter scales and orientation values as parameters as given in Table 2, Table 3 and Table 4 for JAFFE, YALE and FD databases respectively.

• A. Subspace Formation

In this work PCA has been used for intermediate feature reduction for Fisher linear discriminant space. High dimensional data has been de-correlated by PCA method. In this method class variables are not used. Due to this reason PCA is unsupervised. It preserves global

Sb^-$ Ni⁽gi^{- g} I^gi^{- g} IT i-1

Within class scatter matrix Sw be defined as

Sw^-$⁽Ni^-1Si^-.$₁$₁^(gi, j - gi Igz, j - gi Г ⁽⁸⁾ i -1             i-1 j -1

Where gi,j is the n-dimensional pattern j from class Ci, and Ni is the number of training pattern from class Ci, and C is the total number of classes or expression groups. The total meanvector is given by g=N.C Ni               (9)

C Ni gi = N7iS£ aM           (10)

Vector a and matrix i are the unbiased sample mean and sample covariance of matrix of class. In above equation (9) and (10) where N is the total number of samples, that is N=N1+N2+N3 + - - - NC.

Locality Preserving Projection (LPP) approach presented by He et al. [43] preserves local features of input data obtained from affinity matrix (similarity graph information). The input data are projected as same as PCA manner ie S=W^TG. During the preservation of local contents LPP method minimizes the different object function by putting large penalty on neighboring points g_i and gj if both are mapped with larger difference in projected space.

approaches. Consider set of combinational Gabor feature dataset G. where

G = [g₁,-"gN] eRm'N          (14)

The objective function of combinational entire Gabor LFDA is given by arg max ZTSbZ

Z  ZTSwZ

Where Sb and Sw indicates the local inter class scatter matrix and local intra class scatter matrix respectively. Wb and Wiwj indicates the weight matrices of the local inter class adjacency graph and local intra class adjacency graph respectively. Ci is the class label of the data point gi and l e {1,2,- ■ -C} is the class label I this worl heat kernel weight has been used for constructing affinity graph such as Afij min                  2

W ,J₌ Jkgi -^WkSj\\ ^k=U-d (11)

Sb = 1, N WJ(g, -gj'(gi, -gj-f ²,, J =1

Where ^ij is the weight of the connected edge between neighboring points g_i and gj in the affinity graph. Two common methods like heat kernel and cosine model are implemented for computing the value of £у in the input space. If two points are not connected in a same neighborhood then £ij=G. Locality preserving uses affinity graph to compute an optimal projection in an effort to preserve the local structure of the data. The objective function can modified as

Sw = 1 N Wwg - gj Jgi— , 7

²,, J=1

Wb=]

Ary [ iN -117 r^/q=^cj=^l;

VC* CJ

min W_k

WkTGLGTWk

s.t. wfGDGTWk = 1

Ww=‘

.ANJ-• c=^cj=¹;

G,ifCi * Cj

Where L=D-^ is the Laplacian related graph, and D is a diagonal matrix with D,, = £j^y . Then computation of the required projection of subspace solution is obtained from following eigen value problem definition.

GLGTWk = XkGDGTWk (13)

Locality preserving projection based Fisher discriminant Analysis (LFDA) is explicitly preserves the local discriminative features by labeling the classes of different expressions. LFDA is a dimensional reduction method of multimodal data by preserving the local structure of within scatter matrix. By increasing between class scatter matrix variances. For larger variations of features of expressions occurs linear methods fails to give good strength for efficient recognition and classification of expressions. Following section illustrates briefly the three different discriminative based nonlinear subspace

Final eigen vectors corresponding to maximum eigenvalue of the generalized eigenvalue problem is obtained from (15) and given as

S^bZ = AS^wZ (2G)

Objective functions of KLFDA [50], KLSWFDA and KGLSWFDA are obtained by referring our earlier work as mentioned in [23]. All the subspace methods are used to reduce the dimensionality of combinational Gabor space. The reduced dimension space has been named as combinational entire Gabor (CEG) subspace. Expression recognition using all the subspace methods have been named as CEGPCA, CEGICA, CEGFLDA, CEGLPP, CEGLFDA, CEGKLFDA and CEGKGLSWFDA approaches respectively [please refer our earlier work given in open access article [23][24].

B. Creation of CEG Space

Similarity score matrix of combinational Gabor magnitude CGM(Subspace)S and similarity score matrix of combinational Gabor phase CGP(Subspace)S has been computed. Normalized score of combinational Gabor magnitude subspace can be given as

Fig.6. Cropped and preprocessed images JAFFE database

NSCGM (Subspace) =

CGM (Subspace )^ - ^(CGM (Subspace )^ )

Std(CGMSubspace )

Normalized score of combinational Gabor phase subspace can be given as

CGP(Subspace)o - g(CGP(Subspace)o ) SS

NSCGP (Subspace) =                                     ⁽²¹⁾

Std(CGPSubspace )

Final score subspace matrix (Jain, 2005) can be obtained by fusing both CGM and CGP normalized score matrices using maximum fusion rule.

• •    YALE database: This database contains 11 images per person for 15 individuals resulting into a total of 165 images. The images in this database reveal major variations of illumination changes, different facial expressions, and the persons wearing eyeglasses/no eyeglasses not considered. The original size of the images in this database is 243×320 pixels with 256 gray levels. For experiments, the size of these images was scaled down to 64×64 pixels size. Totally 90 (15 personsx6  expression per person images were

CEG(Weighted _ Subspace)

= MAX

[(

NS             + NS

CGM(Subspace)     CGP(Subspace)

)]

Fig.7. Cropped and preprocessed images JAFFE database

Euclidean distance between trained and test image dataset have been computed

^si = |WCEG(W_Subspace)Q^-WCEG(W_Subspace)r||   ⁽²³⁾

Where WC_EG(W_{_}Subspace)T and WCEG(W-Subspace)Q are projected vector final score weight matrices of training and testing combinational entire Gabor subspace images. The image set with lower Euclidean distance has been computed. Based on Euclidean distance metric and RBF kernel based SVM classifier [26] facial expressions were classified.

• •    FD database: This database (FD) consists of 13 subjects and each subject has 75 images with different expressions. In this work 500 images were used with 10 subjects, five expressions such as happy, surprise, angry, sad and neutral. Each class of expression has 100 images. For experiments, all the images are preprocessed and the size of these images is scaled down to 92x92 pixels size shown in Figure 8.

Fig.8. Sample images of FD expression database of size 92x92

• V.    Results and Discussions

• A.    Database Used

The databases used in this work are briefly illustrated below.

• • JAFFE database: In this work, Japanese Female Facial Expression (JAFFE) database was used for experiment [27]. Figure 6 shows cropped samples of JAFFE database. Total 210 images were cropped into 111x126 size. Only required areas like mouth nose, eyes and chin areas has been considered during face detection for extraction of texture features and rest of the part was removed.

Table 2. State of art approaches of JAFFE database