Субволновые линии передачи

Волноведущими структурами (волноводами) называется совокупность элементов, направляющих поток энергии электромагнитного поля. По физическим свойствам выделяются два основных типа волноводных структур: закрытые (экранированные) волноводы (энергия сосредоточена во внутренней полости волновода) и открытые волноводы (основная часть энергии сосредоточена в полости волновода, однако часть энергии распространяется в примыкающем к волноводу пространстве) [1-3]. К экранированным волноводам относятся: металлические прямоугольные, круглые и коаксиальные и др. К открытым волноводам относятся: диэлектрические волноводы, волоконные и интегральные линии различной модификации [3-6].

В волноводных структурах возможно распространение различных типов волн (например, Е -волны и Н -волны) и различных мод, характеризуемых набором целочисленных индексов m и n , которые определяют распределение поля в поперечном сечении волновода [1; 7]. Каждый тип волны и каждая мода характеризуются полосой прозрачности для электромагнитных волн и своей критической частотой, ниже которой волновод теряет свойства направляющей системы. На частотах ниже критической частоты в волноводе энергия не распространяется. Исключением является коаксиальная линия и ее модификации, для которой частота отсечки отсутствует (применяемая преимущественно в метровом и дециметровом диапазонах длин волн).

Широкое применение в микроволновом диапазоне длин волн нашлиэкранированные волноводы (за счет низкого уровня потерь энергии в стенках волноводов и отсутствия излучения). Проблемы широкого использования экранированных волноводов в различных частотных диапазонах связаны с их узкополосностью и большими размерами поперечного сечения. Известно, что поперечные линейные размеры волновода нельзя сделать меньше критических размеров, которые зависят от рабочего типа волны ( Е - и Н -волны), индекса моды ( m , n ) и конструкции самого волновода (прямоугольный, круглый и др.). Критические линейные размеры поперечного сечения волновода сопоставимы с длиной волны направляемого излучения. Это обстоятельство определяет физические ограничения на возможность уменьшения поперечных размеров волноводных структур, что приводит в свою очередь к сложности миниатюризации устройств на базе экранированных волноводов. В обычном режиме их работы (в полосе пропускания) экранированные волноводы не могут быть использованы, в частности, для исследования объектов, размеры которых существенно меньше длины волны используемого излучения. Уменьшение их сечения волноводов переводит работу волновода в запредельный режим с очень высоким коэффициентом затухания. На практике

волноводные структуры в запредельной области из-за большого коэффициента затухания и используются ограниченно (в качестве устройств развязки, отражателей, элементов слабой связи и др.). Для сокращения поперечных размеров экранированного волновода (что особенно актуально в низкочастотной части СВЧ диапазона) можно заполнить внутреннюю полость волновода диэлектриком с высокой диэлектрической проницаемостью ε . Это позволяет сократить поперечные размеры в ε раз на фиксированной частоте или при заданных размерах волноводной структуры уменьшить критическую частоту (максимум на порядок). Практическая реализация этого способа затруднительна из-за сложности стыковки отдельных элементов и температурной нестабильности параметров диэлектриков с высокой диэлектрической проницаемостью.

В статье показано, что введение в экранированные волноводы (с сечением, существенно меньше критического) сред с усилением (активными параметрами) позволяет в запредельных для данного волновода областях частот обеспечить возможность передачи энергии с большим коэффициентом усиления. При этом запредельные свойства волноводов могут быть связаны как с частотной дисперсией заполняющих их сред, так и с пространственной дисперсией самой структуры.

Особенности распространения электромагнитных волн в однородных волноводных структурах

В регулярной цилиндрической волноводной структуре, заполненной однородной изотропной средой, характеризуемой диэлектрической ε и магнитной μ проницаемостями, могут распространяться две группы взаимно независимых Е - и Н -волн. Волновое уравнение для компонент электромагнитного поля Е - и Н -волн может быть представлено в виде:

⊥

-

k z² +

k02εμ

E (x, y, z, t) _ H (x, y, z, t)

= 0 .

Решение ищется в виде распространяющихся вдоль оси z волн:

E (x,y,z,t)

H (x,y,z,t)

E (x,y) 1 . H (x,y)J

exp[i(^t - kz z)].

Подстановка в волновое уравнение дает соотношение: x j 2 + k z 2 = k 02^^:^ , где ^x ^ — поперечное

волновое число, определяемое поперечной структурой волновода.

Распределение поля в поперечном сечении волновода определяется решением двумерного уравнения Лапласа с соответствующими типу волновода граничными условиями на стенках. Решения этого уравнения для прямоугольного волновода соответствуют Emn -волнам и Hmn -волнам. Индексы m, n определяют число вариаций поля вдоль двух поперечных координатных осей структуры x, y. Распределение поля в поперечном сечении волновода для любого типа волн совпадает с распределением этого типа колебаний для стоячей вол- ны при поперечном резонансе, при котором поле вдоль оси волновода неизменно (kz = 0).

В отсутствие затухания для экранирован- ных волноводных структур частота отсечки в отсутствие затухания определяется уравнением kz (to) = 0 . В полосе пропускания выполняется соотношение: k0 εμ > χ ⊥ и продольное волновое число принимает действительные значения. В запредельной области частот к0 д/^й < х± .

Продольное волновое число становится мнимым k z = i (х 1 ) 2 - к 0 ЕМ и определяет уровень затухания, который растет с увеличением числовых значений индексов m , n для всех типов волн (высшие типы волн затухают быстрее, чем низшие типы волн).

При комплексном характере диэлектрической проницаемости среды е = е / + i e // продольное волновое число становится также комплексным и может быть представлено в виде функции:

/        //          2 /               2        2 // kz — kz + ikz — kno b ^  (x± ) + ik0 b ^ .

Действительная часть волнового числа ( к ^ ) определяет фазовую скорость распространения волны для каждой моды в волноводе υ _ф = ω k _z ^/ , мнимая часть волнового числа ( k Z / ) в зависимости от знака е // характеризует усиление или затухание волн. Для анализа физических свойств волновода с усиливающими или диссипативными средами представим волновое число в виде:

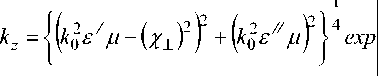
0 ⎫ π 1             k 0² ε ^// μ _⎟⎞

П 2 / 2 2    \._; / _д - ( х _± ) 2 J

при ε ^// <  0

при ε ^// >  0

В полосе пропускания е / ц - х ± >  0 и при малой величине параметра активности среды е // / ( е / м - х J 2 ) <<  1 действительную k Z и мни-¹ \ //               '                                                     "

мую k _z части волнового числа можно представить в виде:

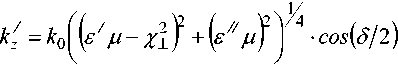
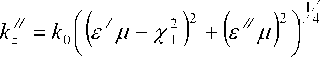
• sin ( 3 /2) ,

В запредельной полосе частот е / м ^- X I <  0 и при малой величине параметра активности среды |£ // / ( f / м ^- X LL ) <<  1 действительную k Z и мнимую k _z ^// части волнового числа можно представить в виде:

_{2               2} 1 ₄

k_z / = k 0 1 ( f / м - X ± ) + ( ^ // M ) I "  sin ( § /2 )

k z/ = ko ^(^/ H - X1)2 + (^ // M)2 ^ • cos(^/2), где δ = arctg

ε ^// μ _⎟⎞

^⎜⎝ε ^/ μ-χ ⊥ ^{2 ⎟}⎠

δ = arctg

⎜ εμ ⎟ ⎜^⎜_⎝ε ^/ μ-χ ⊥ ² ⎟^⎟_⎠

При малом параметре активности среды

При малом параметре активности среды

/            /        2         //         k0ε // μ k z ~ k 0 V^ ^ x 1 ’ k z ^   /—;------*

2 ε ^/ μ - χ ⊥ ²

Тогда относительный параметр затухания (или усиления):

^k z^/

k ₀ ε ^// μ

2 ε ^/ μ - χ _⊥ ²

^k z ^//

≈

k ₀ ε ^/ μ-χ _⊥ ²

Тогда относительный параметр затухания (или усиления):

// kz          ε // μ iz^" 2^-Xa <<1 *

^k z // _ 2 ⁽ g / M - X 1 ¹     1

_{k z}/          _ε // _μ

Из (1) следует, что в полосе пропускания коэффициент усиления kz// (или затухания) волны пропорционален величине параметра активности среды ε // . Из (2) следует, что в запредельной области коэффициент усиления kz// (или затухания) волны обратно пропорционален величине параметра активности среды ε // . При малом // по модулю параметре активности среды ε коэффициент усиления (или ослабления) волны kz// является большой величиной. Этот эффект объясняется малой величиной продольной ком- поненты волнового числа по отношению к поперечному волновому числу kZ << xL. Волна при распространении вдоль оси волновода испытывает многократные отражения от боковых поверхностей и многократно взаимодействует с активной средой на малом отрезке волновода (см. рис. 1). При этом усиление растет при увеличении длины волны (2 > 2cr), а также с увеличением индексов мод m, n. Волноводные моды с высокими индексами имеют более высокий коэффициент усиления.

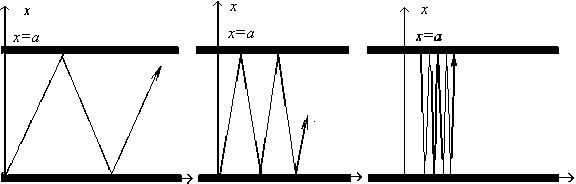
0                      z 0                 z 0                    z

а)                                Ь)                              с)

2 <<  2 cr            2 <  2 cr               2 ~ 2 cr

Рис. 1. Изменение волнового процесса с увеличением длины волны вплоть до критической λ _cr

Для всех мод Е - и Н -волн в экранированных структурах волноводов нет отсечки во всем диапазоне частот, где £ // >  0 . Этот эффект наблюдается независимо от типа волноводных экранированных структур с полным или частичным заполнением активной средой.

Дисперсионные характеристики прямоугольноговолноводасактивными и диссипативными средами

Рассмотрим распространение электромагнитных волн в прямоугольном металлическом волноводе с идеальными металлическими стенками, однородно заполненном изотропной средой с диэлектрической проницаемостью _g = _g / + ig // , ^ = 1 . Размер широкой стенки волновода равен a , размер узкой стенки – b . Направление распространения электромагнитных волн совпадает с осью z .

Из уравнений Максвелла следует, что в структуре возможно распространение взаимно независимых: E _0mn - и H _0mn -волн. Волновые уравнения для компонент поля Е - и Н -волн имеют вид:

Решение волнового уравнения с учетом граничных условий на стенках волновода:

E y , z ⁽ x = ^{0 )} = E y , z ^{( x} = a ⁾ = ⁰ ;

E x , z ( y = 0 ) = E x , z ( y = b ) = 0

ищется в виде:

f ^E zmn ⁽ r ,t ) 1 lH zmn ( Г , t )/

E 0 mn

H 0 mn

^{sin ( k} xm ^{x ) sin ( k} yn y ⁾

COs ( k xm X ) co^{s ( k} yn У 1

^ X

x exp\i(tot - kzmnz)], где E0mn,H0mn – постоянные, определяемые условиями возбуждения, kxm = тПaa , kym = ППbb .

Уравнение для продольного волнового числа k имеет вид: zmn

_⎜⎛ ∂ ² ∂ ²     ∂ ²

^⎜⎝∂ x ²    ∂ y ²    ∂ z ²

⎞ к02 (f / + i£ // ju

⎠

'E( r, t Л H( r , t J

= 0

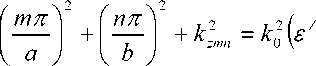
+ i £ ) p .

Критическая длина волны λcrmn и критическая частота f crmn для моды с индексами m, n оп- ределяются в виде

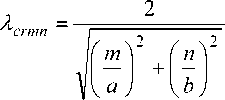
^f crmn

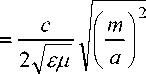
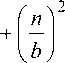
Волны с индексами m , n могут распространяться в диапазоне длин волн X <  X crmn . Область длин волн λ > λ _crmn является запредельной. Число распространяющихся в волноводе на заданной частоте волн (мод) определяется индексами m , n и зависит от поперечных размеров волновода и частоты. Например, для группы волн с индексом n = 0 число распространяющихся мод m = [ 2 a / X ] . Число распространяющихся мод увеличивается с ростом частоты.

Продольное волновое число к „ = к' „ + ik /' zmn zmn zmn определяется соотношением:

к zmn k02 ε / μ

-

-

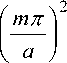
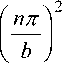
. .,2 //

+ ik ₀ ε μ

Введение в полость структуры среды с усилени-ем,характеризуемым параметром ε ^// > 0 , приводит к тому,что в запредельной области возникают условия распространения энергии с усилением волн.Из дисперсионного уравнения следует, что k zm k "_т >0 при 8 >  0 и направление распространения волны совпадает с направлением роста её интенсивности.

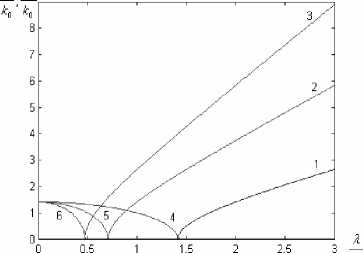
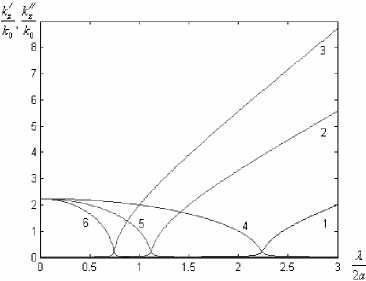
На рис. 2.показаны дисперсионные характеристики продольного волнового числа для активной среды для волн трех мод (Н10,Н20, Н30) при различных параметрах структуры. С ростом индекса моды уменьшается критическая длина волны и растет коэффициент усиления в запредельной области длин волн.Из графиков следует,что величина коэффици-// ента усиления среды £ в малой степени влияет на коэффициент усиления структуры.Более существенное влияние на волновое число оказывает изменение действительной части диэлектрической проницаемости среды в полосе пропускания (рис.2б.).

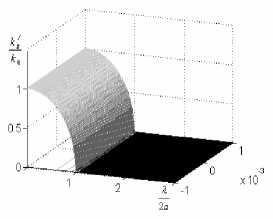
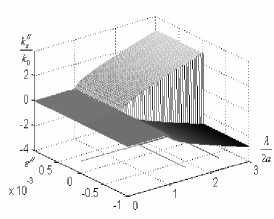
Из графиков рис. 2видно,что в области длин волн меньших критической длины волны, различной для разных мод (индекса m) и зависящей от диэ-/ лектрическойпроницаемости среды ε , расположены зоны пропускания kz/ >> kz// . В запредельной области выполняется соотношение kz// >> k Z > 0, волна распространяется в зависимости от знака ε // с высоким затуханием или усилением. На рис. 3а-б показана зависимость действительной и мнимой частей волнового числа от параметра активности среды,который меняется в пределах от –0,001 (диссипативная среда) до +0,001 (усиливающая среда) для моды m = 1.

к"

2a

a )

б )

Рис. 2. Дисперсионные характеристики структуры (коэффициент усиления – кривые 1- Н ₁₀ , 2- Н ₂₀, 3- Н ₃₀ , волновое число – кривые 4 - Н ₀, 5- Н ₂₀, 6- Н ₃₀ , a - £ ^/ = 2 , £ // = 0,01 , б - £ / = 5 , £ "  = 0 , 1 )

a )

б )

Рис. 3. Дисперсионные характеристики прямоугольного волновода с волной Н ₁₀

Изменение абсолютного значения параметра ε // в малой степени влияет на мнимую часть волнового числа, которая скачкообразно меняется при изменении знака параметра активности среды. Это позво- ляет получить хорошие параметры усиления при относительно малом параметре активности среды. На рис.4 показаны дисперсионные характеристики волн типа Н mn в волноводе.

Хорошо известно [1; 7-8],что распространение волнового пакета с плавно меняющейся огибающей

(то есть с узким спектром частот)в среде с дисперси-

, где k z ( ^ ) - волновое число,

ей,но без поглощения,происходит с групповой скоро- ⎛ dk _z ^{- 1}

стью υ _gr = ⎜

⎝ dω ⎠

ω – частота волны.В полосе пропускания среды или волноводной структуры групповая скорость электро-магнитнойволны всегда меньше скорости света и сов- падает со скоростью распространения энергии волны [1;,8]и скоростью распространения комплексной огибающей узкополосного сигнала.

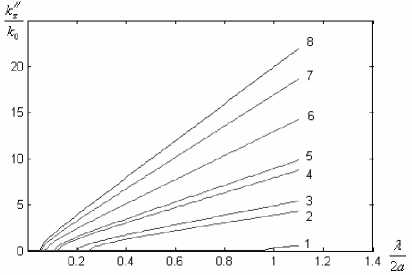
Рис. 4. Дисперсионные характеристики волн типа в прямоугольном волноводе ( а = 2 b , Н ₀-1, Н ₂₀-2, Н -3, Н ₃₀-4, Н ₂₁-5, Н ₃₁-6, Н ₁₂-7, Н ₂₂-8) ^{1 11}

В случае сред с поглощением (усилением) обычно считается [7], что понятие групповой скорости теряет смысл, так как групповая скорость, введенная обычным соотношением в неконсервативных средах, уже не является скоростью переноса энергии волны. Кроме того, она оказывается (как и фазовая скорость) комплексной, что приводит к вопросу о физическом смысле результатов, полученных из выражения для υ _gr . В [9] показано, что использование понятия комплексной групповой скорости сигнала (и комплексного времени его задержки) для сигналов, огибающая которых описывается аналитической функцией, не противоречит известным фактам.

Понятие комплексной групповой скорости при описании распространения импульсов в усиливающих средах позволяет повысить точность результатов. Комплексную групповую скорость можно считать обобщением понятия групповой скорости на случай поглощающих или усиливающих сред. Вещественная часть групповой скорости и Re = Re [ u _gr ] характеризует скорость движения сигнала в пространстве. Мнимая часть групповой скорости и gm = Im [ u _gr ] характеризует не перемещение сигнала, а изменение формы его комплексной огибающей. С учетом этого фазовую скорость будем определять в виде:

υф =

ω

/ zm

ω

ω

Re 2 ε /μ

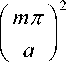
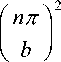
ω ²

+ i ₂ ε ^// μ c ²

Групповая скорость:

с ² Re ω ε ^/ μ

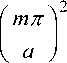
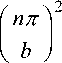
ω

+ i ₂ ε ^// μ c ²

ωε/μ

dk _zmn

υ _gr = Re ⎜         ⎟

⎝ d ω ⎠

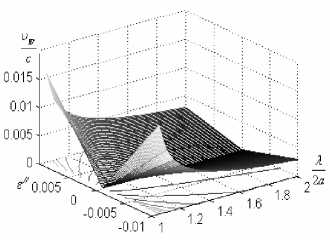
Рис. 5. Дисперсия групповой скорости

На рис.5 показана дисперсионная характеристика групповой скорости в запредельной области длин волн. Таким образом,для эффективности усиления поперечное сечение волновода с активной средой необходимо уменьшить до минимума,величина которого определяется технологическими требованиями, уровнем передаваемой мощности и др.

Необходимо иметь в виду, что наряду с рабочим типом волны усиливаются с большим коэффициентом усиления и высшие типы волн.

Круглый волновод с активной средой

Рассмотрим распространение электромагнитных волн в запредельной области частот круглого волновода с металлическими стенками радиусом r = a, однородно заполненного активной средой.

Для круглого металлического волновода с осью волновода z и радиусом r = a , волновые уравнения для E mn - и H _mn -волн имеют вид:

воде. В запредельной области частот (2 >  2 _cr ) усиление растет с увеличением индексов мод и увеличением длины волны (уменьшением радиуса волновода).

Рассмотрим открытую волноводную структуру в виде цилиндра, однородно заполненного средой с параметрами £ = £ / + i £ // , д , расположенного в среде с параметрами £ 1 , ^ 1 . Волновые числа в волноводе и во внешней среде удовлетворяют соотношениям:

-

⎜⎛ ∂2 + 1 ∂ + 1 ∂2 + ∂2

⎜⎝ ∂r2 r ∂r r2 ∂α 2 ∂z2

k ₀

ε

/

⎞

+ ie // ) u

⎠

E _z ( r , a , z , t ) H z ^{( r , a} , z , t )

= 0.

Решение ищется в виде

^k 2 = ^k o^£i A + p 2 ,

k2 = k2£/Ц - (x±)2 + ik02£//^ ,

где p –поперечноеволновое числововнешнейсре-де. Необходимым условием канализации энергии является соотношение: ε ^/ μ > ε ₁ μ ₁ . В этом случае

E z ( r , a , z , t ) H z ( r , a , z , t )

/     x fcos(na)!

= AJn (XnmrX . /   .[exlHin - kzz)]

[ sin(na )J где Jn (xr) — функции Бесселя. Для Hmn - волн поперечное волновое число χ nm = Bmn a является корнем уравнения JП (ха) = 0, которое соответствует граничному условию на электрических стенках круглого волновода радиусом r = a:

ET (r = a) = 0 ; Ea (r = a) = 0 .

Для E _mn – волн поперечное волновое число χ _nm = A _mn a является корнем уравнения: J n ( xa ) = 0 , которое соответствует граничному условию: E _T ( r = a ) = 0 , то есть E _a ( r = a ) = 0 .

Критические длины волн для E _mn - и H _mn -волн в круглом волноводе могут быть найдены в виде:

⎧2πa Bmn для Hmn-волн

^λ crmn ⁼ ⎨

⎩2πa Amn для Emn-волн

Продольное волновое число определяется в виде:

k02ε/μ-⎜ mn ⎟ + ik02ε //, Emn - волны;

к =< zmn

a

k02ε/μ-⎜ mn ⎟ + ik02ε //, Hmn - волны

a

В полосе пропускания выполняется соотношение k02 £ /ц > Xmmn, в запредельной области kо £ ц < Xmn. На рис. 6 показаны дисперсионные характеристики волн типа Еmn в круглом волно- числовые значения продольного волнового числа находятся в диапазоне k0 д/e / ^ > kz > k0 ^£1ц1 .

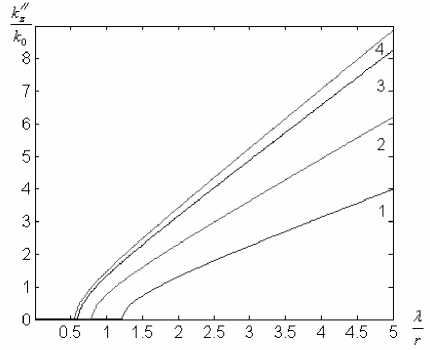
Рис. 6. Дисперсионные характеристики низших мод в круглом волноводе с активной средой в запредельной области частот (кривая 1 – Е ₀₁; кр. 2 – Е ₁₁; кр. 3 – Е ₂₁; кр. 4 – Е ₀₂). ^{1 11}

Открытый волновод теряет свойство канализации энергии при условии, что продольное волновое число становится равным волновому числу прилегающего к волноводу пространства: k _z = k 0 ^£ 1 ^ 1 . В этом случае энергия не концентрируется в области диэлектрического волновода, а излучается в соседние области пространства. Различие в структуре поля на критических частотах приводит к тому, что в открытых структурах коэффициент усиления является малой величиной и в области прозрачности, и в запредельной области частот при малых параметрах активности среды.

Заключение

Введение усиливающей среды в полость волновода с запредельными размерами позволяет получить существенно большее (на несколько порядков) усиление сигнала в запредельной области длин волн по сравнению с усилением в области пропускания волновода, заполненного такой же средой. Одновременно наблюдается увеличение фазовой скорости и уменьшение групповой скорости распространения волн. Анализ показывает, что коэффициент усиления остается высоким даже при малых значениях параметра усиления среды.

Усиление в запредельной области частот наблюдается для всех типов волн. Усиление возрастает при уменьшении поперечных размеров волноводной структуры (меньших критического значения a < a _mcr ). Усиление при заданном параметре a/X растет также с увеличением m и п, то есть моды с высокими индексами имеют больший коэффициент усиления.

Таким образом, для получения высокого коэффициента усиления целесообразно использовать волноводные структуры сверхмалых (субволновых) поперечных размеров m. Это показывает принципиально новую возможность сверхминиатюризации волноводных компонентов схем за счет использования активных сред. Это особенно актуально, например, в дециметровом диапазоне длин волн и в низкочастотной части СВЧ диапазона. Выбор минимальных размеров волноводов в этом случае ограничен только допустимым уровнем передаваемой мощности и проблема- ми технологии производства. При этом обеспечить возможность передачи достаточно высокого уровня мощности можно за счет накачки в волновод активного газа [2], пробивная напряженность поля в котором выше, чем у воздуха.