Super Resolution of PET Images using Hybrid Regularization

Published Online January 2017 in MECS DOI: 10.5815/ijigsp.2017.01.01

Positron Emission Tomography (PET) scanners provide quantitative imaging of physiological processes within the body. The analysis of these processes is helpful in diagnosing and monitoring of several diseases such as cancer, epilepsy, and many others [1][2].

For PET studies, a radiotracer is administered to a subject; since the radiotracer is a radioactive substance it emits positrons that produce a pair of photons during decay. Counts of pairs of photons are registered by the scanner to reconstruct the final image. The resulting PET images are a representation of the distribution the radiotracer in the body.

PET has found major uses in clinical practice and research. However, the images produced tend to be of low signal to noise ratios (SNR) and of limited spatial resolution, the former due to several phenomena such as scattering of photons and limited photon-count availability, and the later mainly due to positron range and sensor size [27][28]. These problems in the image could affect the estimation of physiological parameters causing variations in the quantitative and qualitative accuracy of the studies using PET [3].

The problem of poor resolution in PET images has been treated by improving instrumentation of the scanner [4], however, these solutions are expensive and sometimes made for a particular scanner. Another approach is to use super-resolution (SR) techniques from signal processing. Multiframe SR consist of processing several observed low resolution images (LR) to obtain a high resolution (HR) image, these methods work under the premise that each observed LR image have subpixel shifts different from the other LR images and thus providing new information to reconstruct a HR image.

There exist several works in the literature aiming to solve the problem of low resolution, we review some of the most relevant algorithms proposed in the literature. In [17] a robust approach is proposed by incorporating the use of a median estimator in order to reject outlayers in the data, this method report very good results and a low computational cost, however it lacks of a proper justification as pointed out by [22]. In [16] it is proposed a Bayesian methodology to account for the SR problem, the authors also apply a variational inference methodology to find the hyper-parameters associated with the model in addition they apply a total variation regularization term to stabilize the SR problem. The results are very promising however the time required to complete a reconstruction could be prohibitive in some applications such as PET.

There exists also literature of SR applied to the enhancement of PET images, in [5] it is described the use of super resolution applied to PET images, such study is based the approach of [6], where a high resolution (HR) image is estimated through back projecting the error between several observed low resolution (LR) images and the LR version of the estimated HR image, this study demonstrated the feasibility to apply SR techniques to PET imaging. The work in [7] introduced a scheme improving the resolution in the sinogram domain, in which data is obtained through wobbling motion. The described algorithm obtains a HR sinogram estimation using interpolation following by the reconstruction using expectation maximization. The authors in [8] introduced a modified expectation maximization (EM) algorithm to reconstruct HR images starting from LR sonograms, reporting high quality of the images at a reasonable processing time.

Some of the reviewed techniques used existing techniques without regularization or incorporate the SR model in to the reconstruction process which could be time consuming especially if only certain areas/volumes of the study need to be of high resolution. The problem of how the regularization terms affects the produced HR resolution PET image has not been widely explored nor the use of SR techniques on post reconstruction images.

In this paper we present a hybrid approach to regularize the problem of low SNR and poor spatial resolution. Our goal is to reduce the noise in the PET images especially at lower count rates and at the same time to increment the resolution of these images. We use a multi-frame SR technique aimed to work on post reconstruction data. This could be an advantage, in processing time, if only a small area needs an improvement in resolution, such as in classifying small lesions.

The rest of the paper is organized as follows. In Section 2, we review the PET and SR models, Section 3 present related works, Section 4, described the proposed algorithm, Section 5 presents experiments and results, and finally, conclusions are provided in Section 6.

• II.    Models

• A.    Positron Emission Tomography

A PET scanner consist of several rings. Each ring contains blocks of scintillation crystal sensors, see Fig. 1, which captures photons produced by the decay of the radiotracer. The most common form of decay of PET rediotracers is beta decay, where a positron is emitted and subsequently annihilated by an electron. At each annihilation point a pair of photons is emitted and the scanner ring must detect both photons in order to count for a valid event [23]. Counts of events are then stacked by angle and position from the center of the scanner to form sinograms, which are used by image reconstruction techniques, such as filtered back projection, to produce the final image. Reconstructed images from PET data are used in this work to test our proposed scheme.

The PET images suffer from low SNR caused by several factors that degrade the counting process, such as: scatter events, occurring when a photon scatter within the patient; random coincidences, in which two separate events result in the detection of only one because attenuation or scatter of the second photon; and the limited amount of radiotracer that can be administered to the patient [23]. Also, PET images have a limited spatial resolution which is caused by a large crystal width, scanner diameter, and positron range [8]. Other factors such as the positron range are limited by the physics of the medium and cannot be altered. Therefore, alternative techniques such as SR are developed, in order to improve the resolution of PET images.

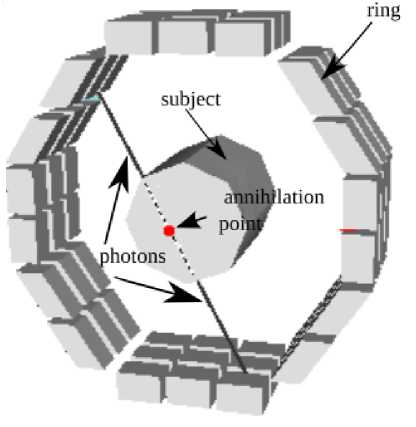
Fig.1. PET scanner, each ring is composed of a block of several sensors. The trayectory of each pair of photons emitted from the annihilation point is collinear and the event is detected with two sensors of the scanner.

• B.    Super Resolution Image Observation Model

The aim of multi-frame SR techniques is to produce a high resolution image from a set of multiple low resolution images. Each image of the set, is acquired with sub-pixel shifts relative to each other, they may also have additional degradations such as blur and noise.

In the SR formulation, it is assumed that the degradation of a HR image x, produces the set of L low resolution images Y_k and that the degradation process producing the LR images consists of the following phenomena: warping, which is caused by translation of the bed of the scanner or movement caused by patient breathing; blurring that appears as a result of the crystal width, random positron paths, non-collinearity, etc [5]; and down-sampling which is inherent to the number and position of the scanner sensors. Thus, following [9] the degradation process of a HR PET image x of N₁×N₂ is formulated as

Y_k = DB_kM_kx + n_k , k = 1,..., L , (1)

Where x is represented as a vector of N1N2×1, Yk is the L1N1L2N2×1 vector representation of the kth observed image. Mk, Bk, and D are matrices modeling warping, blur and downsampling, respectively, and nk is the noise in the kth observation. Numbers L1 and L2 are the downsampling factors in the vertical and horizontal directions respectively. In this work we assumed that the matrices Mk and Bk are known in advance and D is a downsample by two operator. We also suppose that the L observations, Yk, are given. For a description of the procedure of how to obtain such images we refer the interested reader to the works of [10][11][12][13] where are discussed several techniques, e.g., scanner wobbling, dichotomic motion, and bed shifting.

• III.    Related Work

The scheme proposed in this paper consists in the inclusion of a regularization term which is a combination of a total variation (TV) term and a Tikhonov regularization term.

The TV term has been widely used in image processing and related inverse problems, it was introduced by [24] in the context of image denoising, and assume that natural images can be well approximated by piece wise constant functions.

The TV scheme has been successfully employed to reduce heavy noise while at the same time preserve the edges in the image [25]. However, TV suffers from staircasing effects in homogenous regions [25][26] which is not desirable in the context of medical image. On the other hand, another technique, Tikhonov regularization, which effectively removes the noise in homogeneous regions without incurring in undesirable effects, has the problem of blurring the edges of the image severely. Thus, a regularization combining the two terms as been applied in the literature [14][15], in order to minimize the number of artifacts introduced to the image and simultaneously preserve the edges of the image, this regularization has been applied to solve several problems of image processing. The hybrid regularization term has the form

^ || x |k + (1 - 2 )P||2 (2)

where λ is a regularization parameter and ||∙|| TV is the TV seminorm. The model (2) has been employed in [14] to reduce noise in images denoising, while in the work of [15], is implemented a proximal point method for solve a hybrid model in image restoration. The model is applied to denoising, debluring and impainting.

• IV.    Proposed Scheme

In this work we suggest to include the hybrid regularization in the objective function to solve the problem of SR in PET images, we also proposed to balance both terms using anatomical information and thus minimize artifact in homogeneous zones while preserve edges and small structures in the high resolution result.

Since reconstructed PET images reflect the radiotracer distribution of the subject under study, images tend to be on most areas similar to a piecewise constant images and this depend on the type of tissue that absorbs the radiotracer. Thus the TV regularization in combination with the Tikhonov regularization are expected to perform well in the PET image, preserving the areas of constant radiotracer absorption and the edges of possible lesions.

For this reason, here we proposed to include (2) in the degradation model of SR, thus we modify the SR objective function as:

L

J ( x ) = £ I Y k - DB k M k xI I² + M | x | I TV k = 1

+ (1 - Я )|| х ||².                      (3)

The desire HR estimate is found by minimizing (3), that is x = arg min J(x)                (4)

x

To solve (4) a gradient descent scheme is used, the Euler-Lagrange equations are as follow:

L

J '( x ) = £ ( DB k M k ) t ( DB k M k ) x

K = 1

L

• - ^ ( DB _K M _K ) tY_K + z\-    - + (1 - 2 ) V x   (5)

K = 1                            ^{11 V} x ¹¹

Additionally, we proposed to balance the terms of the regularization by obtaining the parameter λ using anatomical information. For this end, we obtain an estimate of the HR image using bi-cubic interpolation with one LR image, I_LR .

If we expect to remove most of the noise without blurring the edges, then in homogeneous regions we need to put in the Tikhonov term more weight, while in zones with edges we need that the TV term to prevail, in this paper we attain this with an edge map. The generation of the edge map follows an approach similar to [16]. We use a smoothing filter based on a Gaussian by convolving the a LR image, I_LR , with a Gaussian kernel, G , and then, since changes in intensity occurs at extreme values in the first derivative, we use the magnitude of the gradient of the image to estimate an edge map.

EdgeMap = | V ( G * I lr )||²          (6)

The proposed algorithm to solve the SR problem for PET images is presented:

Algorithm 1 : Hybrid SR

Input: set of LR images

Result : HR image

(a)                                                     (b)                                                      (c)

Fig.3. High resolution images obtained with a) Zomet method, b) TV method, and c) proposed method.

(a)

(b)

(c)

Fig. 2. Phantom images a) original software phantom, b) reconstructed image from simulation, and c) edge map of the reconstructed image.

• V.    Results

In this section, we describe the results of the tests we conducted, in order to demonstrate the effectiveness of the proposed scheme. We also make comparisons with methods in the literature: a TV method proposed in [15], and the Zomet method, proposed in [16].

We also used the SimSet software [18] which is based on Monte Carlo simulation techniques to model the instrumentation and physical processes of the scanner, thus allowing to simulate accurately a PET studies through the use of phantoms which are physical or software models of diverse objects, human beings or animals.

In all the experiments conducted we used a scale factor of two and seven iterations ( IterMax=7 ) of the proposed algorithm and т=0.2 .

• A.    Phantom study

We used a phantom to study the effect of resolution on small structures. The phantom consisted of four rows of cylinders with radii of 5, 4, 3, and 2 mm . Each cylinder is filled with activity equivalent to ¹⁸F-fluorodoxiglucose. A simulation was carry out using SimSet and then four datasets were replicated adding degradations to the PET data: blur, rotation and translations. The phantom, the image resulting from a simulated scan, and the edge map are shown in Fig.2.

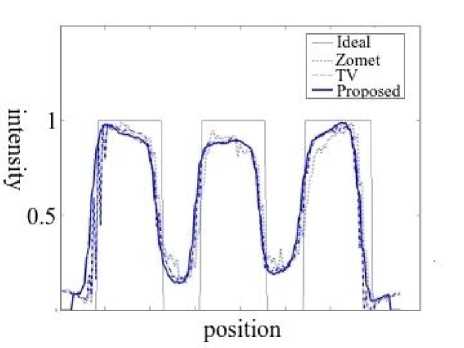
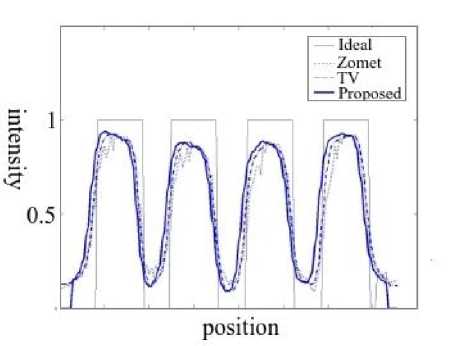
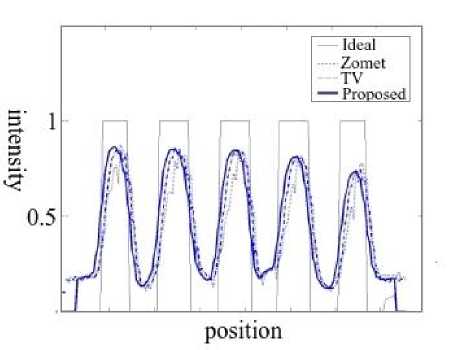
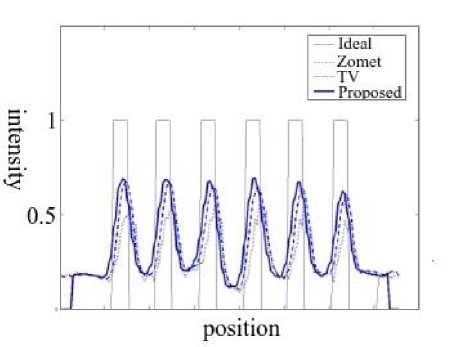
The simulated scans were processed with the different methods using a scale factor of two, the resulting HR images are show in Fig. 3. Profiles of pixel values across each row of cylinders were taken and its graphs are depicted in Fig. 4. From these graph the curves corresponding to the proposed method show less noise without degrading the peaks a valleys of the curves with respect to the other methods. For the graph of Fig. 4c corresponding to the cylinder of 2 mm diameter, it can be seen that the TV and proposed method achieve the higher difference between maximum and minimum value (contrast).

For a second experiment, we designed a PET phantom for SimSet based on the DigiMouse atlas which was generated from CT and cryosection images of a 28g male mouse [20]. Additionally, we place a small sphere inside the liver section of the phantom to simulate a lesion of 1 × 1 mm and contrast to background ratio of 7:1. Four PET scans were simulated with SimSet. Instead of the original vector of translations/rotations of the LR images, a vector contaminated with Gaussian noise of zero mean and variance of 0.5 pixels was used with the different methods. In this way, we simulated errors in the determination of the warping matrix and verify the robustness of the different methods to such errors.

The original and the edge map of the image obtained from a scan simulation are show in Fig. 5a and 5b respectively. The SR processed images are show in Fig. 6. Zooms of the region of the lesion are shown in Fig. 7. Because the error in the values of the warp matrix all methods generate artifacts, in the zooms of Fig.7 it can be seem that the proposed method has less artifacts than the other methods. We also evaluated the lesion preservation and as a figure of merit, we use the lesion to background defined in [21] as

= M L - M B             (7)

LB

LB    MB where ML denotes the mean value within the region of the lesion and MB indicates a 1.6 × 1.6 mm squared a region in the liver that does not contain the lesion. Results of the CLB for the different method are reported in Fig. 8. The values of CLB for the proposed and TV methods are very similar, this could be the result because the lesion have a very well defined edge and in that region the proposed method gives more emphasis to the TV term.

(a)

(b)

(c)

(d)

Fig.4. Graphs of profiles across each row of cylinders. a) 5 mm, b) 4 mm, c) 3 mm, and d) 2 mm.

(a)                                                    (b)                                                    (c)

(a)

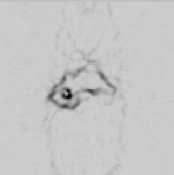
(b)

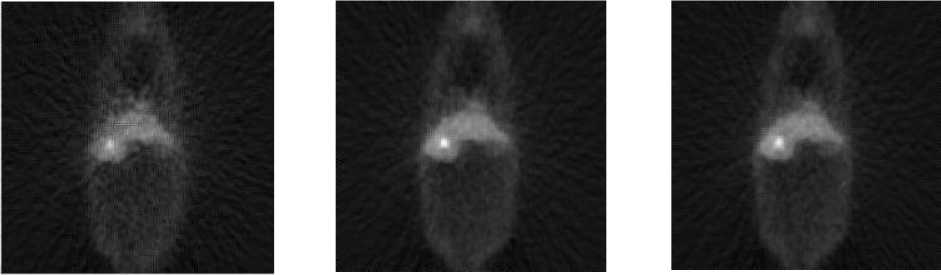
Fig.5. DigiMouse phantom. a) simulated scan, b) edge map.

Fig.6. High resolution DigiMouse a) Zomet method, b) TV method, and c) proposed method

(a)                           (b)                           (c)

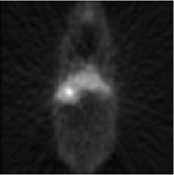
Fig.7. Zooms of the DigiMouse phantom. a) zomet method, b) TV method, and c) proposed method.

■ CNR

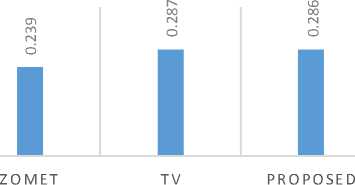
Fig.8. Graphic of the CNR attained for each method.

• B.    Acquired data study

We test our algorithm with data collected from a real scanner using a small a rat. Data was acquired with the stationary quad-HIDAC scanner, located at Wolfson Molecular Image Centre in Manchester, United Kingdom, the data acquisition time was 30-min and was reconstructed using the EM, 0.5-mm sided voxels, one iteration, and 50 subsets. No corrections for attenuation, random, and scatter events were applied.

From the original reconstructed image, we generate four LR images with the following settings: downsampling factor was set to two, a 1 mm FWHM Gaussian was used for the blur matrix; and two rotations, ±3 and ±5 degrees and translations of ±5 mm where set in the warping matrix. A LR image, obtained with the aforementioned settings is show in Fig. 9a. The calculated edge map of the rat image is displayed on Fig. 9b.

The HR images obtained after being processed with the different methods are depicted in Fig. 10. From these images, it can be seen that the resulting image processed with the zomet method presented more artifacts than the other two methods, also, it is observed that the proposed method preserves better the structures on the interior of the rat body, to better appreciate this, a zoom of a section on the inside of the rat body, the lower leg of the animal, is shown in Fig. 11. From image zoom, it can be observed, that the border of the activity zones (in black) in the image processed with the proposed method present less staircasing effects and structures are better preserved than the image processed with the TV method, this due to the combination of TV and Tikhonov regularization.

(a)

Fig.9. Rat from the quad-HIDAC scanner. a) Low resolution image, b) edge map.

(b)

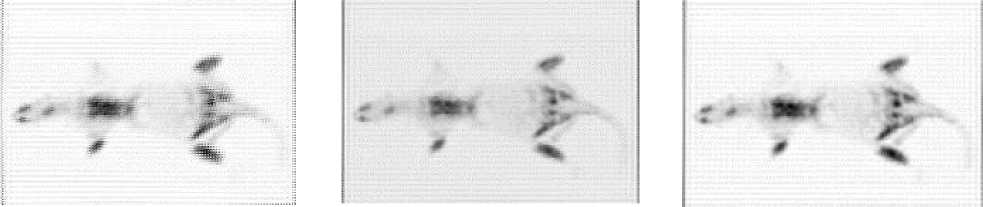
(a)                                                     (b)                                                      (c)

Fig.10. High resolution images from the rat scan, using: a) Zomet method, b) TV method, and c) proposed method. The vertical artifacts appearing on all images are due to lack of normalization in the reconstruction method used to process the original acquired data.

(a)                         (b)                         (c)

Fig.11. Zoom of the images shown in Fig. 4. a) Zomet method, b) TV method, and c) proposed method.

In Fig. 12, we show the Peak Signal to Noise Ratio (PSNR) and if Fig. 13, the structural similarity index (SSIM) [19, 29] for the results on the acquired data. It can be seen that the proposed method was the best of the evaluated methods, confirming quantitatively the observations for the rat image.

The time required to execute the different algorithms is show in Fig. 14. The experiments were tested in a computer with Pentium core i7 Dual-Core CPU T4400 @ 2.20GHz, with 5.8 GB of RAM and all methods were implemented on Matlab 16. The proposed method achieves the minimum processing time.

• VI. Conclusions

In this paper, we present a method for obtain a high resolution PET image through a multiframe superresolution scheme. In our proposed algorithm we stabilize the super resolution problem using a hybrid regularization scheme, consisting of a total variation term and a Tikhonov based term. We proposed to balance the two terms using anatomical data from an estimated of the HR image using the bicubic method, thereby, we enforce preservation of borders through the TV term and noise reduction with the Tikhonov term.

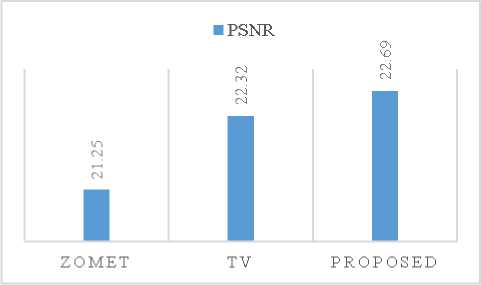
Fig.12. Graphic of PSNR attained for each method.

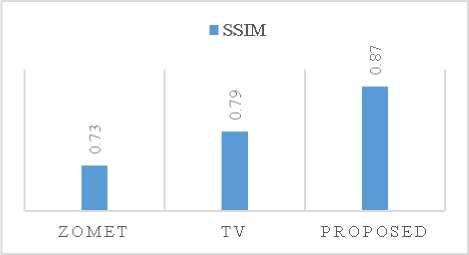
Fig.13. Graphic of SSIM attained for each method.

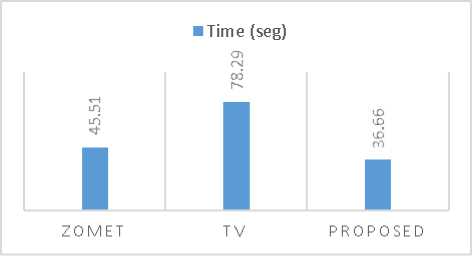
Fig.14. Graphic of the computation time attained for each method.

We have tested the proposed algorithm with simulated and acquired data. In the first experiment we evaluated graphically the contrast on small structures and in a second experiment we verify the performance under errors in the estimation of the warping of the LR images, in a third experiment the proposed method was tested on real data. On all experiments the performance of the proposed method was better or similar than other comparison methods, however our method took less time to run which can be an advantage for implementations on real scanners.

As a future work we plan to investigate more techniques to calculate the weights by adding a priori information from other modalities like computer tomography or magnetic resonance imaging. Also investigate the effect of pre-process the images with methods to reduce noise such as [30][31] before applying the SR method.

Acknowledgment

This research was supported by the program for teaching development PRODEP UACJ-PTC-333. The authors are grateful for this support.