Supercapacitor as a buffer electrical source for induction motor

Цитирование: Сайфулин, Р. Ф. Суперконденсатор как буферный источник электроэнергии для аcинхронного двигателя / Р. Ф. Сайфулин // Журн. Сиб. федер. ун-та. Техника и технологии, 2022, 15(8). С. 940–947. DOI: 10.17516/1999-494X-0431

various ways of calculating this model. [2,3,4,5,6,7] However, these methods use vector multiplication, Euler transformations, and the substitutions that are made when calculating differential equations lead to a large number of terms in the equation. Therefore, this article proposes the calculation of the asynchronous motor model in a rotating coordinate system during the transition from a three-phase system to a two-phase one.

Mathematical calculation of the induction drive model

Initially, the induction drive is a three-phase electric machine with an implicit-pole rotor, it is proposed to simplify this model to a two-phase one. To simplify the mathematical description of induction drive, the space vector method turned out to be suitable. The method allows linking the rotor flux linkage equations into a single system with vector state variables. The essence of the method is that the instantaneous values of symmetric three-phase state variables (voltage, currents, flux linkage) can be mathematically transformed so that they are represented by one space vector. We represent a system of equations with vector state variables for the case with an arbitrary orientation of the coordinate system.

VT^T»

^rsTs+dl S +jaA	(1.1)
и     dTR Vf R  R R    dt       k   m  R	(1.2)
Ts=xs i s+X m iR	(1.3)
^ = xR i R+xm i S	(1.4)
m = kMod ( ^ i I k )	(1.5)
dϑ m T m    =mm c	(1.6)

Here US, UR, iS, iR, ΨS and ΨR are two-element vectors of voltages, currents and flux linkages, presented in an arbitrarily oriented orthogonal (two-phase) coordinate system in the form of components along the coordinate axes. The variable ωk is used to set an arbitrary frequency of rotation of the coordinate system. The auxiliary matrix constant j serves to “flip” the components of vector variables and simplifies the form of writing the system of equations. rS, rR – Resistance of stator and rotor, m- torque.

Expanding the content of space vectors, the flux linkage equations 1.3, 1.4 are substituted into the stator and rotor voltage formulas, while equating 1.2 to zero, since the electric motor is short-circuited.

"~*      —*

U S =r S i S +

d(x_sTs +X m   :

dt

^+ak ⁽ xS^+x m^ R )

U R =r R i R +

d( x _R i R +x m i S )

dt

+j ( a k -p& m )( X R i R +X m Ts ) =0

The change in the rotor current vector is expressed from equation 3

diR^ Tr^ x_mX .    . xm^.   !TR dt =-xRiR-xR dt- jαkiR-jαkxRiS+jpϑmxR

The rotor current vector is expressed from equation 1.4 and then substituted into equation 4

—> iR =

"TFT* ^ Ψ_R-x_mi_S

— x_R

di R dt

rRXm^R Tr^S x2R   +  x2R

"> F^        FTP           TFT xm diS   xm ΨR      xm ΨR

-jαk      +jpϑm xR dt     xR         xR

Equations 5 and 6 are inserted into equation 2 to calculate the stator voltage vector

X s dTs _ r R X m У _R

S S S dt     x2R

rRx2miS xmdis xR dt +jpϑ

x2R

-

._m^X- X m ⁱl+a_kc _ST_S-^{jja k X m i S} x_R            x_R

The following replacements are introduced

2 r=r S +k R r R

(8.1)

x m k_R=

'

xR x2m

(8.2)

x S =x S -_xR

T R = ^{X R} r R

Let’s describe the vectors of stator and rotor voltages with introduced substitutions

(8.3)

(8.4)

x^' di ^⃗⃗             k ^⃗ Ψ ^{⃗⃗⃗⃗ ⃗}

^⃗ U ^{⃗ ⃗} S =r S i ^⃗ S ^⃗ +      + jα k x^'_Si ^⃗ S ^⃗ -      +jpϑ m k R ^⃗ Ψ ^⃗⃗⃗⃗ R ^⃗

⃗ Ψ ⃗⃗⃗ ⃗ ⃗    d ⃗ Ψ ⃗⃗⃗ ⃗ ⃗

⃗ U ⃗ ⃗ R =- k R r i ⃗ S ⃗ + ^R + ^R +j ( α k -p ϑ m ) ⃗ Ψ ⃗⃗⃗ ⃗ R ⃗ =0

^R     T_R     d t

In the case of coordinates orientation along the stator flux linkage, the moment can be expressed from equation 1.5 as m = ΨSαiSβ⃗ - ΨSβiSα⃗

In this case, the stator flux linkage vector from equation 1.3 is transformed by replacing the rotor current vector from equation 5

(⃗⃗⃗⃗⃗⃗-⃗

R m S)(12)

x _R

And this equation 12 of the stator flux linkage vector can now be written along the axes, taking into account the replacements 8.1–8.4

⃗Ψ⃗⃗⃗S⃗⃗α⃗=x'Si⃗⃗S⃗⃗α⃗+kR⃗Ψ⃗⃗⃗R⃗⃗α⃗(13)

⃗Ψ⃗⃗⃗S⃗⃗β⃗=xSi⃗⃗S⃗⃗β⃗+kR⃗Ψ⃗⃗⃗R⃗⃗β⃗(14)

Accordingly, in the equation of moment 11, it is possible to replace the vectors of the stator flux linkage along the axes

m  =kR(⃗Ψ⃗⃗⃗R⃗⃗α⃗i⃗⃗S⃗⃗β⃗-⃗Ψ⃗⃗⃗R⃗⃗β⃗i⃗⃗S⃗⃗α⃗) (15) Space vectors of stator voltage, stator current, rotor flux linkage can be described by these equations Us=USx+jUSy (16.1) i =i +ji S  Sx   Sy (16.2) 1R^Rjy (16.3) As a result of changes, substitutions and transformations, the system of equations 1.1– 1.6, which mathematically describes the work of the induction drive in a rotating coordinate system, will take the following new form fT =  х^„.- . k. x    x    dt      S y TR   x   m     y (17.1) x dT       . k ___,       ___, USy=riSy+  dt  -αkxSiSx- TR ΨRy +pϑmkR ΨRx (17.2) Urx 0 1 ^^ (17.3) U. =0=117 +^.,77+(a.„S 717 y     TR   y   dt        y        m   x (17.4) m =k8 (^-^) (17.5) d^m^m-mc Tm dt =m-mc (17.6) 1 Accepting TS=— the system of equations 17.1-17.6 transforms into operator form k Ux=r(1 +Tsp)isx-akXsisy-   TRx-p9mkR TRy (18.1) '--^)™4 -".'x (18.2) 1 U..=0=1R(1+r.p>1..-k.7.iSx-("k-p»m )1Ry (18.3) у U.y 0  7. (1 +TrP) 1Ry k.rRiSy+(ak p9m) 1rx (18.4) ^Ai^U (18.5) Xp9m =m-mc (18.6) From equations 18.1, 18.2 the stator current is expressed '      kR                        1 (19) iSx=(USx+αkxSiSy+   ΨRx-pϑmkR ΨRy) TR               r (1+TSp ) iSy=

'      ^{k R}

( ^USy - ^ak^xS i Sx ⁺ tp ^ Ry^-p ^ m^kR ^ Rx )

r ( ^{1 + T}S P )

And from equations 18.3, 18.4 the rotor flux linkage is expressed

T

Ψ R x = (k R r R i S x +(α k - pϑ m ) Ψ Ry   ^R                                            (21)

R x    R R S x    k m Ry _1+TRp

T

Ψ Ry = (k R r R i Sy - (α k - pϑ m ) Ψ R x     ^R                                                (22)

1+T _R p

The speed from equation 18.6 will be

ϑ m =    (m-m c )

Tmp

Thus, from the obtained final equations 19–23, a mathematical model of induction drive in a rotating coordinate system was created. At the same time, this model was transformed from a three-phase into a two-phase one – Fig. 1.

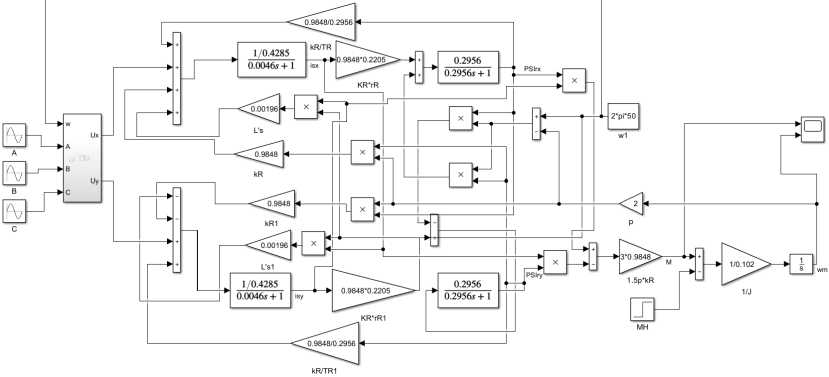
Fig. 1. Model assembled in Simulink

Imitation modeling

In this paper, a model of an AIR 160S 4 induction electric motor is considered with the following parameters presented in Table 1.

Table 1. AIR 160S 4 parameters

Motor	Power, kW	Speed, rpm	Voltage, V	Efficiency, %	Power factor	к In	M M n	max ——— M n	Moment of inertia, kgm2
AIR 160S 4	15	1450	400	89.5	0.86	7,7	2.2	2.6	0.075

To assess the adequacy and correctness of the assembled model, it was proposed to compare it with the induction motor model from the standard Simulink/Simscape library – Fig.2.

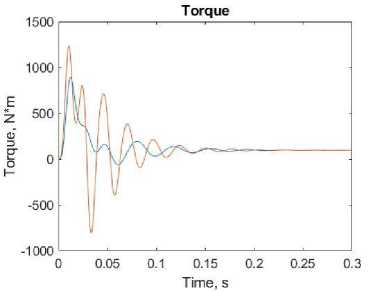
The rotor speed and the torque developed by the motors are shown in the Fig. 3 for the model in a rotating coordinate system – blue, and for the standard model – orange.

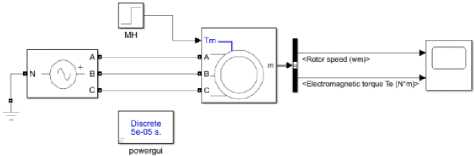
Fig. 2. Standard model of an induction motor in Simulink

Speed

о. 1000

о- 500 (Л

(a)

-500 L 0

0.05     0.1     0.15     0.2    0.25     0.3

Time, s

(b)

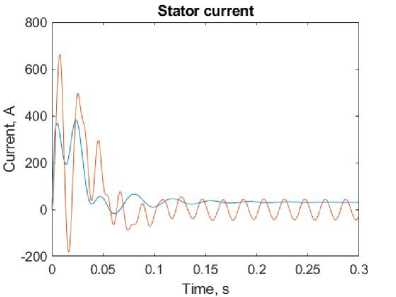
Fig. 3. Output characteristics of electric drives: a – speed, b – torque, c – stator current

(c)

From the obtained characteristics, it can be seen that the output values coincide, and the processes take place at the same time. However, the system from the standard library is more oscillatory, so the model in the rotating coordinate system has a better transient process. It is planned to compare these models with a real electric drive to obtain the most accurate results in further researches.

Conclusion

Mathematical substitutions in the equations and the used methods have shown the adequacy and correctness of their use. Analysis of the data, obtained from simulation modeling of the developed model, showed small discrepancies with the standard block from the Simulink library. The use of the obtained mathematical equations, as well as the model assembled in Matlab Simulink, will make it possible to qualitatively evaluate the operation of an induction drive in statics and dynamics. This model will be used in future research, including the creation of a buffer power source based on a supercapacitor for an induction electric drive.