Суперпозиция двух смещенных с оптической оси пучков Лагерра-Гаусса

Оптические вихревые пучки являются объектом пристального внимания ученых из-за того, что, хотя эти пучки известны уже более 40 лет, остается много нерешенных вопросов. Одной из важных характеристик вихревых пучков является топологический заряд (ТЗ), для расчета которого известны два альтернативных подхода. Для всего пучка ТЗ равен сумме ТЗ каждого отдельного оптического вихря, внедренного в пучок. А ТЗ отдельного вихря (винтовой дислокации) равен целому числу скачков фазы на 2π при обходе по замкнутому контуру вокруг центра винтовой дислокации (центра фазовой сингулярности) [1]. Это достаточно затруднительный подход, так как требует нахождения всех центров винтовых дислокаций или изолированных нулей интенсивности в пучке. Известен и другой, более конструктивный подход к расчету ТЗ всего вихревого пучка со множеством винтовых дислокаций [2]. Он заключается в определении целого числа скачков фазы на 2π при обходе по окружности бесконечного радиуса (чтобы учесть при расчете все винтовые дислокации, внедренные в пучок). В этой работе мы будем использовать второй подход.

Одна из проблем, связанная с ТЗ, заключается в том, что нет доказательства его сохранения при распространении вихревого пучка в свободном пространстве. Но есть работы, в которых показано, что ТЗ не сохраняется [3 –7]. Другая проблема связана с определением ТЗ суперпозиции нескольких оптических вихрей. Например, хорошо известно, что ТЗ пучка Ла-герра–Гаусса (ЛГ), амплитуда которого имеет сомножитель exp( in φ), где φ – полярный угол в плоскости сечения пучка, равен n . А чему равен ТЗ осевой суперпозиции нескольких ЛГ пучков с разными ТЗ? Оказывается, ТЗ такой суперпозиции равен большему ТЗ, который есть у отдельных пучков ЛГ [5]. А какой ТЗ будет у суперпозиции смещенных с оси пучков ЛГ до сих пор неизвестно. Еще вопрос, который требует своего решения. Если в Гауссов пучок внедрить в разных точках две одинаковые винтовые дислокации с ТЗ, равным n , то очевидно, что ТЗ всего пучка будет равен 2 n . А чему равен ТЗ суперпозиции двух одинаковых смещенных с оптической оси Гауссовых пучков, в которые внедрены винтовые дислокации с одинаковым ТЗ n ? Оказывается, как показано в данной работе, ТЗ такой суперпозиции равен n .

В данной работе мы найдем теоретически и численно ТЗ двух пучков ЛГ с номерами (0, n ) и (0, m ), симметрично смещенных с оптической оси. Мы покажем, что у суперпозиции из двух одинаковых пучков ЛГ ( n = m ), смещенных с оптической оси, ТЗ равен n . Будет также показано, что у суперпозиции двух смещенных пучков ЛГ с определенными наклонами к оптической оси (такими, чтобы суперпозиция являлась структурно-устойчивым пучком) ТЗ бесконечный, так как при сложении таких пучков на некоторой линии формируется бесконечное число винтовых дислокаций с ТЗ + 1. Вихревые пучки с бесконечным ТЗ исследовались в недавних работах [8, 9].

Структурно-устойчивая суперпозиция смещенных пучков ЛГ

Согласно теории спиральных пучков [10, 11], любая функция вида

Видно, что функция (3) имеет вид (1): Гауссова экспонента, умноженная на функцию, аргумент которой равен x +i y . Функцию (3) можно записать компактнее:

E ₁( x , y ) = exp

x ² + y ² 1

----— x w2 J

N (2(x + iy)(xn -iyn)) xY En exp —----Y------ x n=0                   w2

x ( x + iy - x_n - iy_n ) m n .

Чтобы определить ТЗ суперпозиции (4), рассмотрим для простоты комплексную амплитуду в начальной плоскости ( z =0) суперпозиции только двух структурно-устойчивых пучков (4), симметрично смещенных с оптической оси вдоль горизонтальной координаты на величину x 0 :

( x ² + V ² I /

E ( x , y ) = E o exp I--;— I f ( x ± iy ) ,

V w ² J

где E 0 - постоянная, / (x) - любая целая аналитическая функция, описывает структурно-устойчивый Гауссов пучок. У такого пучка конечная энергия, и при распространении он сохраняет структуру распределения интенсивности в своем сечении, изменяясь только масштабно и вращаясь. Самое существенное в (1) состоит в том, что знак у аргумента функции / ( x ) в (1) должен быть либо плюс, либо минус. Только в этом случае пучок будет сохранять структуру. В качестве примера рассмотрим суперпозицию смещенных однокольцевых пучков ЛГ, которая является структурно-устойчивой:

( ( x - x ₀)² + y ²   2 ix_oy 1

E i ( x , y ) = A exp | -      °²-+ Y Ix

V       w ²         w ² J

x ( x - x ₀ + iy ) m +                                     (5)

„ ( ( x + x ° ) ² + y ²   2 ix ° y Y        . _v

+ B exp l------— I ( x + x ° + iy ) ,

V       w ²         w ² J

где A и B – постоянные, n и m – топологический заряд каждого из пучков в суперпозиции (положительные целые числа), w – радиус перетяжки Гауссова пучка, ( x , y ) – поперечные декартовые координаты. Топологический заряд суперпозиции (5) будем искать по формуле Берри [2]:

N

E i ( x , V ) = Y E n exp n =0

( x - x n )² + ( y - V n )² w ²

1 r _T 2L) ^{d E} ( ^r , ^ф ) / ^дф TC = —limIm d ф--—— —,

2 n r ^~ J        E ( r , ф )

2 i ( x n y - y n x )Y

■--;------ ( x ^- x n w ²

m n

+ iy - iy n ) ,

где ( x n , y n ) – координаты смещения центра пучка в суперпозиции, w – радиус перетяжки Гауссова пучка, E n – весовые коэффициенты (постоянные комплексные числа), m n – топологический заряд каждого n -го пучка в суперпозиции. Если во втором слагаемом в экспоненте в (2) будут другие ( x n , y n ), то пучок (2) не будет структурно-устойчивым. Чтобы убедиться, что суперпозиция смещенных пучков ЛГ (2) является структурно-устойчивым пучком, вынесем из (2) общую для всех Гауссову экспоненту:

.       ( x ² + y ² 1

Ei( x, y) = exp--

V

VF ( xn2 + УпY2(x + iy)(xn - 1Уп )) x> En exp------■Ц n=0       V     w2              w2

x ( x + iy - x_n - iy n ) m .

где ( r , φ) – полярные координаты в поперечной плоскости, Im – мнимая часть числа. Подставим (5) в (6) и получим:

1            ^{2 n}

TC = —limIm f d ф { A Г imre^{i ф} ( re^{i ф} - x ₀) ^{m - 1} + r ^”

^П 0

+ 2 ix ₀ re^{i ф} ( re^{i ф} - x 0 ) ^m

w ²

+ B inre ^ф ( re ^ф+ x ₀) ^{n 1}

( 2 x ₀ re^{i ф} I exp II ⁺

V w ² J

2 ix ₀ re^{1 ф} ( re^ + x ₀) ⁿ

w ²

x (7)

( 2 x0 rei^Y I _        .      ( 2 x0 re^\ x exp--H- x < A(reiф - x0)m exp ------- +

V      w ² JI I                    V w ² J

-1

( 2 xre^{i ф} 11

+ B ( re^{i ф} + x ₀ ) ⁿ exp I---— I ^

V      w ² JI

Интеграл по φ в (7) разобьем на два интеграла:

n/2    3 t /2

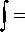
J + f

-n/2 n/2

В первом интеграле в (7) значения косинуса cos ф будут положительные. Поэтому в пределе r ^ да слагаемые в (7), у которых в качестве сомножителя имеется экспонента с минусом, будут стремиться к нулю. В (7) первый интеграл будет тогда иметь вид:

Анализировать (11) в общем виде затруднительно. Для простоты пусть m = n и | A | = | B |. Тогда вместо (5) получим, что на вертикальной оси ( x =0) амплитуда суперпозиции будет иметь вид:

1 п/2

—limIm J" d ф { A [ imre* ^ф ( re i ^ф 2 л ^r -» _^ ₂

- x о ) ^{m - 1} +

Г A \ П 2 , n /2 Г x о ² + У ² ) E 1 (x = о, y ) = 2 A ( x о + y ² ) exp I-- 2— |x

2 ix 0 re i ^ф ( re i ^ф- x 0 ) ^m 1     Г 2 x 0 re i ^ф VI

+---------2------- exPI---Г" V x w2        J I w2 V J

I 2 x о y x cos I---— - n arctan

I ww

y x0

x { A ( re i ^ф

x 0 ) ^m exp

Г 2 x 0 re i ^ф

I w ²

-1

= —Im [ d ф< A ( im - ² ix ⁰ re ) r m e n^ 2 n                    ww

-n/2     I L

Из (12) видно, что на вертикальной оси будут располагаться нули амплитуды или центры фазовых сингулярностей (винтовые дислокации) с ТЗ, равным + 1 каждая ( n – четное):

Г 2xоre^ YL          Г 2xоeY x exp I---------l ^{ A(reiф)m exp I---------l 1

V w2 J J               ( w2 J J m2x

= — +--lim r .

2   n w ^{2 r} ^”

2 x о y       . y I n

---— - n arctan I —l = —+ n p , p = о,1,2,...

w ²             I x _о J   2

Во втором интеграле в (7) значения косинуса cos ф будут отрицательные. Поэтому в пределе r ^да слагаемые в (7), у которых в качестве сомножителя имеется экспонента с плюсом, будут стремиться к нулю. В (7) второй интеграл тогда будет иметь вид:

—limIm [ dф{BГinreiф(re*ф+ x0)n-1 -r^»

2П

2 ix 0 re i ^ф ( re^ + x 0 ) n w ²

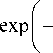
2 x 0 re^ I w     J.

2 x 0 re i ^ф

-1

x { B ( re i ^ф + x 0 ) n exp

-

w ²

Таким образом, бесконечный ТЗ суперпозиции (5) при условии, что m = n и | A | = | B |, объясняется бесконечным числом винтовых дислокаций, центры которых расположены на вертикальной оси в точках (13). В общем случае из (11) видно, что винтовые дислокации будут лежать на кривой, которая с ростом модуля y отклоняется в сторону положительных x (при n >  m ) и в сторону отрицательных x (при m >  n ). На вертикальной оси y будут только две точки сингулярности, которые следуют из уравнения (11) при x =0.

Так как суперпозиция (5) структурно-устойчивая, то при распространении распределение интенсивности будет вращаться, и прямая линия, на которой расположено бесконечное число сингулярностей, тоже будет вращаться. То есть бесконечный ТЗ суперпозиции (5) будет при любом z .

1 I           2 ix^re ф

= —Im Г d ф< B ( in --) r n e 'n ^ф

^{2 п} i I L       ^{w 2}

-1

Суперпозиция двух несмещенных пучков ЛГ

Положим в (5) x 0 =0, получим комплексную амплитуду двух соосных однокольцевых пучков ЛГ:

x exp

А Г x ² + y ² |

E ( x , y ) = exp--- — x

I      w ² J

n 2 x 0

= —+---lim r .

2 n w ^{2 r} ^”

Складывая вместе значения двух интегралов (8) и (9), получим, что топологический заряд (7) равен бесконечности:

n + m 4 x о

TC =--1-- lim r ^ да .

2      n w ^{2 r} ^^да

Найдем объяснение тому, что ТЗ суперпозиции (5) бесконечный. Приравняем модули обоих слагаемых в (5), так как именно в точках ( x , y ), в которых модули двух слагаемых равны, возникают фазовые сингулярности. Получим:

A

B

Г 4 xx 0 exp I -"V

I w ²

L ( x + x о )² + У ² J n /2

L ( x - x о )² + y ² J m /2

x

nm

( x + iy । _,[ x + iy I A Il + B I-------- l

w

w

.

В (14), по сравнению с (5), мы добавили для учета размерности радиус перетяжки w . Можно показать [5], что ТЗ суперпозиции (14) равен n (при n > m ) или m (при m >  n ). При этом на оптической оси находится оптический вихрь с меньшим ТЗ (пусть m ), а на радиусе окружности

r = w

B

A

1/( n - m )

разделенные одинаковыми расстояниями, лежат остальные ( n – m ) сингулярностей порядка +1. Итого ТЗ пучка (14) равен m +( n – m )= n .

Суперпозиция двух смещенных с оси пучков ЛГ

При смещении с оси двух однокольцевых пучков ЛГ не получится структурно-устойчивая суперпозиция (5), а получится суперпозиция структурно-устойчивых пучков. Хотя сама суперпозиция уже не будет структурно-устойчивой. В этом случае мы получим комплексную амплитуду вида:

Аналогично для второго интеграла в (16) получим выражение:

1              3n/2

—limIm [ d ’ { B Г inre i ’ ( re^z ’ + x ₀) ” ^{- 1} +

2nr^~    j i n/2

w ²

+ 2 x ₀ r sin ’ ( re i ’ + x ₀) ⁿ

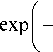
2 x ₀ r cos ’ w ²

E 2 ( X , y ) =

= A exp

( X - X 0 ) 2 + y ² Y x - X 0 + y 2                      11

w ²      JV w

+ B exp I -

( X + X 0 ) 2 + y ² V X + X 0 + iy 1 "

w ²

.

w

Подставив (15) в (6), получим:

1 2л,                                        i

TC = —lim Im J d ’ { A ^mire^ re i’ -x , ) ^{— 1}

2 x , r sin ’ re ’ - x 0 ) ^—

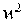
I2 x, r cos ’ exP I---2—

I     w ²

+ B

. . . . , 2xr sin’(rei’+ x )" i nre ’( re ’ + x,) "-1 + —---—----— w2

x { B ( re i ’ + x ₀) ⁿ exp

^{- 1}

2 x ₀ r cos ’ 11

w ²      JI

1         3л/2        I

= —Im Г d ’< B ( in + 2 n

3n/2

n/2

I 2 x o r cos ’ll x exp-- ^ x ^p I                            I

V w ² JI

² x 0 r ^sin ’ ) _rn_ezn ’ w ²

^{- 1}

I _x I 2 x ₀ r cos ’ 11 n x J B ( re i ’ ) ⁿ exp || J = — .

V       w ²     J 2

x

Складывая результаты (17) и (18), получим, что топологический заряд суперпозиции (15) равен

TC =

n + —

x exp l- 2 xr cos ’ IU A„ - x _Г exp l 2 x r "'” |+

+ B ( re i’ + x o ) "  exp

( 2 x , re ’

V    w ²

Интеграл по φ в (16), аналогично интегралу (7), разобьем на два интеграла

2n n/2 3n/2

J = J + J .

0 -t /2 t /2

В первом интеграле в (16) значения косинуса cos ’ будут положительные. Поэтому в пределе r — да слагаемые в (16), у которых в качестве сомножителя имеется экспонента с отрицательным показателем степени, будут стремиться к нулю. Поэтому для первого интеграла получим значение:

1             л/2

—limIm J d ’ { A [ i—re i ’ ( re i’ -x , ) ^{— - 1 2 n r} -П/2

2 x , r sin ф ( re ’ - x q)'

I 2x,rcos’ll exp --------- rx pI 2 I

V w JI

^{- 1}

x { Are • - x , ) — exp [ -c's ’ H

V w JI

Из (19) следует замечательное свойство смещенных с оси двух одинаковых однокольцевых пучков ЛГ: если m = n , то ТЗ всей суперпозиции равен ТЗ только одного пучка TC = n . Это означает, что две одинаковые винтовые дислокации, разнесенные в пространстве, имеют ТЗ, как одна дислокация. Наверное, это свойство можно распространить на несколько смещенных с оси одинаковых пучков ЛГ. Косвенным подтверждением этому является то, что орбитальный угловой момент (ОУМ) суперпозиции смещенных одинаковых пучков ЛГ равен ОУМ одного пучка, который равен топологическому заряду n [12].

Если смещение большое ( x 0 >>  w ), то пучки почти не будут интерферировать, и ТЗ, казалось бы, должен быть равен просто сумме ТЗ отдельных пучков TC = n + m . Но последнее утверждение неверное (хотя интуитивно кажется, что верное), так как ТЗ суперпозиции Гауссова оптического вихря с плоской волной (или широким Гауссовым пучком)

I r ² . 1

E2 (r, ’) = A + rn exp+ zn’ , (20) V w2 J где A – постоянная плоской волны, распространяющейся вдоль оптической оси, равен нулю:

1 _т^п/ 2      I           2 x o r sin’_x

= —Im   d ’J A ( z — --—) r^-e ’

^{2 п}    -П/2     I L          w ²

^{- 1}

( 2 x, rcos ’]1I.,           [ 2 x, rcos ’ll     — xexp|----------I^< A( re ’)— exp|----------I^ =—.

V w ² JI I V w ² JI       2

2n

TC = —limIm [ d ’x inr" exp 2 n r       J

A + r " exp

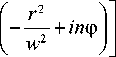
= 0.

r ²

- + zn ’ w ²

x

Причем равенство нулю в (21) будет при любой сколь угодно малой постоянной величине A. Это происходит потому, что вблизи оптической оси на окружности радиуса, примерно равном r=1A 1/n,

сформируются n оптических вихрей с ТC = 1, а на окружности большего радиуса, который удовлетворяет уравнению

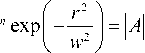
сформируются еще n оптических вихрей с TC =– 1. Таким образом, два смещенных на большое расстояние пучка ЛГ нельзя рассматривать независимо и складывать их ТЗ. При любой величине смещения ТЗ должен определяться уравнением (19).

Моделирование

Цель моделирования – подтвердить (или опровергнуть) выражение (19). Комплексная амплитуда суперпозиции двух смещенных однокольцевых пучков ЛГ имеет вид:

E ( x, y ,0 ) = A

x exp w2

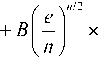
"1 m iy )

n

x --- ( x + x ₀ + iy ) exp w

^^^^ .

C0 ) 2 + y² w ²

где ( x , y ) – декартовы координаты в начальной плоскости, w – радиус перетяжки, x 0 – смещение обоих пучков относительно оптической оси (первый пучок смещён вправо, второй – влево), m и n – топологические заряды пучков ЛГ, A и B – весовые коэффициенты суперпозиции. Постоянные множители после весовых коэффициентов введены для выравнивания максимальной интенсивности на кольцах обоих пучков.

На рис. 1 показано распределение интенсивности и фазы суперпозиции (24) для следующих параметров: λ =532 нм, w 0 =500 мкм, m =2, n =5, A = B = 1, x 0 / w : 0 (рис. 1 а , б ), 0,3 (рис. 1 в , г ), 0,6 (рис. 1 д , е ), 0,8 (рис. 1 ж , з ). Расчётная область | x |, | y | ≤ R ( R =5 мм).

Из рис. 1 видно, что при отсутствии смещения ( x 0 =0) топологический заряд суперпозиции (24) равен 5. То есть ТЗ равен большему из двух ТЗ ( m =2, n =5). А при смещении две винтовые дислокации из 5 с ТЗ + 1 компенсируются двумя винтовыми дислокациями с ТЗ – 1, пришедшими из бесконечности. И ТЗ всей суперпозиции смещенных пучков ЛГ (24) равен 3. Эта цифра является средним арифметическим двух ТЗ m =2, n =5, взятым с недостатком:

TC =( n + m –1)/2=(2+5–1)/2=3.

Причем ТЗ, равный 3, будет сохраняться при любой величине смещения x 0 .

смещениях x 0 / w 0 : 0 (рис. 1а, б), 0,3 (рис. 1в, г), 0,6 (рис. 1д, е), 0,8 (рис. 1ж, з)

Далее зафиксируем m и будем варьировать n . На рис. 2 показано распределение интенсивности и фазы суперпозиции (24) для следующих параметров: λ =532 нм, w =500 мкм, m =2, n =3 (рис. 2 а , б ), n =4 (рис. 2 в , г ), n =5 (рис. 2 д , е ), n =6 (рис. 2 ж , з ), n =7 (рис. 2 и , к ), n =8 (рис. 2 л , м ), A = B = 1, x 0 / w =0,5 (рис. 2 а , м ). Расчётная область | x |, | y | ≤ R ( R =5 мм).

По распределениям фазы на рис. 2 были получены следующие значения ТЗ: 3 ( n =3), 4( n =4), 3 ( n =5), 4( n =6), 5 ( n =7), 6( n =8). Эти числа равны числу скачков фазы на 2π (прямые линии, с одной стороны которых черный цвет, а с другой стороны белый цвет), которые достигают до границ картины фазы на каждом кадре фазы на рис. 2.

Из рис. 2 видно, что для n =5, 6, 7, 8 ТЗ суперпозиции (24) (m =2) оказался равен TC = n –2, так как две винтовых дислокации с ТЗ + 1 были скомпенсированы двумя винтовыми дислокациями с ТЗ –1, пришедшими из бесконечности. А для n =3, 4 топологический заряд всей суперпозиции оказался равен TC= n. В этом случае все винтовые сингулярности остались у суперпозиции (24) такие же, как и при отсутствии смещения.

m = 2, n = 3 (рис. 2а, б), n = 4 (рис. 2в, г), n = 5 (рис. 2д, е), n = 6 (рис. 2ж, з), n = 7 (рис. 2и, к), n = 8 (рис. 2л, м), A = B = 1, x 0 / w = 0,5 (рис. 2а-м).

Расчётная область | x |, | y | ≤ R (R = 5 мм)

Результаты на рис. 2 можно интерпретировать и с помощью формулы (19). Тогда для m =2, n =3 получим TC =( n + m )/2+ 1/2=3, для m =2, n =4 получим TC =( n + m )/2+ 1 =4, для m =2, n =5 получим TC =( n + m )/2– 1/2=3, для m =2, n =6 получим

TC =( n + m )/2=4; для m =2, n =7 получим TC =( n + m )/2+ 1/2=5 и для m =2, n = 8 получим TC =( n + m )/2+ 1 =6. То есть если сумма m + n четная, то ТЗ суперпозиции равен полусумме плюс 0 или 1, а если сумма m + n нечетная, то ТЗ суперпозиции (24) равен полусумме (19) плюс 1/2 или минус 1/2. Осталось выяснить, когда надо к (19) добавлять указанные числа или отнимать их. Моделирование показало, что для любых номеров n и m (проверили до m <3, n < 10) ТЗ суперпозиции (24) может быть равен одному из 4 целых чисел, выражения для которых приведены в табл. 1.

Табл. 1. Варианты ТЗ суперпозиции двух смещенных с оптической оси пучков ЛГ, которые следуют из результатов моделирования (рис. 1, 2)

ТЗ всей суперпозиции TC 1 =( m + n )/2 TC 2 =( m + n +2)/ 2 TC 3 =( m + n + 1)/2 TC 4 =( m + n – 1)/2

То есть какой из вариантов ТЗ суперпозиции надо выбрать, зависит от четности или нечетности суммы двух ТЗ каждого пучка ЛГ. Физический смысл того, что к значению ТЗ (19) суперпозиции (15) следует добавить или отнять 1/2 (если сумма n + m нечетная), объясняется тем, что у светового поля не может быть дробного ТЗ. Топологический заряд светового поля должен быть целым, за исключением начальной плоскости, в которой ТЗ может быть задан дробным как граничное условие. Но при распространении пучка в пространстве его ТЗ становится целым. В нашем случае нет граничного начального поля, а есть сумма двух смещенных ЛГ-пучков в плоскости перетяжки. То есть в начальной плоскости ( z =0) пучки (24) уже распространяются, и их ТЗ должен быть целым.

Чтобы получить правила выбора вариантов ТЗ суперпозиции, приведенных в табл. 1, рассмотрим подробнее уравнение (11), при выполнении которого могут появиться дополнительные сингулярности (пусть для простоты A = B ). При большом положительном x вместо (11) можно записать:

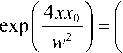
x ² + y¹ w ²

( n - m )/2

Из (25) видно, что решением может быть точка (x, y), у которой обе координаты большие, чтобы правая степень (n > m) сравнялась с левой экспонентой. Это означает, что в первом и четвертом квадрантах появится четное число 2p оптических вихрей с координатами (x>0, ±y) и с ТЗ -1, которые скомпенсируют 2p оптических вихрей с ТЗ + 1. Во втором и третьем квадрантах декартовой системы координат «компенсирующие» оптические вихри появиться не могут, так как при больших отрицательных x <0 уравнение (25) не будет иметь решений. Потому что левая часть (25) будет близка к нулю, а правая будет много больше 1 при любом y. Аналогично можно показать, что на декартовых осях также не могут возникнуть «компенсирующие» вихри. Действительно, при x =0 вместо (11) получим уравнение

/ ~      ~ х ( n - m )/2

1 J x 0 + y ² j

V w ² У

которое не имеет решения при больших y² . При y =0 (на горизонтальной оси) вместо (11) получим

( 4 xx 0

exP I

V w²

( x + x 0 ) n ( x - x 0 ) m

Решения (27) при больших положительных x нет, так как экспонента будет больше, чем степень. Решение может быть при небольших x > 0. Но «компенсирующие» вихри должны прийти из бесконечности, и поэтому они не могут появиться на горизонтальной оси. Таким образом, качественный анализ уравнения (11) показал, что «компенсирующие» вихри с ТЗ – 1 появляются при смещении x 0 только в первом и четвертом квадрантах ( x > 0, ± y ) и уменьшают топологический заряд суперпозиции на четное число 2 p , равное числу скачков фазы на 2π у суперпозиции (24) при отсутствии смещения ( x 0 = 0):

TC = n - 2 p = n - 2[ n - 1/4] - , n >  4, (28)

где знак «квадратные скобки с минусом» означает взятие целого числа с недостатком.

Теперь зафиксируем m =3 и снова будем варьировать n . На рис. 3 показано распределение интенсивности и фазы суперпозиции (24) для следующих параметров: λ =532 нм, w 0 =500 мкм, n = 1, 2, 5, 6, 7, 8, 9, C 1 = 1, C 2 = 1, x 0 / w 0 =0,5. Расчётная область | x |, | y | ≤ R ( R =5 мм).

По распределениям фазы на рис. 3 были получены следующие значения ТЗ : 3 ( n = 1), 2 ( n =2), 5 ( n =5), 4 ( n =6), 5 ( n =7), 6 ( n =8), 7( n = 9), 6( n = 10). Эти числа ТЗ равны числу скачков фазы на 2π (прямые линии, с одной стороны которых черный цвет, а с другой стороны белый цвет), которые достигают до границ картины фазы на каждом кадре фазы на рис. 3.

Рассчитанные численно по общей формуле (6) ТЗ суперпозиции двух смещенных пучков ЛГ, которые показаны на рис. 2 и 3, сведены вместе в табл. 2.

Из сравнения рис. 2 и 3 можно заметить, что при перестановке ТЗ у пучков ТЗ всей суперпозиции изменяется. Действительно, из рис. 2 видно, что при m =2 и n =3 получим TC =3, а из рис. 3 видно, что при m =3 и n =2 получим TC =2. Можно показать, что это свойство не инвариантности ТЗ к перестановке двух пучков в суперпозиции верно для любых двух в сумме нечетных номеров n и m .

n = 1

n = 2

n = 5

n = 6

n = 7

n = 8

n = 9

Рис. 3. Распределение интенсивности и фазы суперпозиции (24) для следующих параметров: λ = 532 нм, w 0 = 500 мкм, m = 1, 2, 5, 6, 7, 8, 9, C 1 = 1, C 2 = 1, x 0 / w 0 = 0,5.

Расчётная область | x |, | y | ≤ R (R = 5 мм)

Табл. 2. ТЗ суперпозиции (24) при разных n и m

	n = 0	n =1	n =2	n =3	n =4	n =5	n = 6	n = 7	n =8	n =9	n =10
m =2	2	1	2	3	4	3	4	5	6	5	6
m =3	2	3	2	3	4	5	4	5	6	7	6

На основе уравнений (19), (25–28) и на основе результатов численного моделирования (рис. 1 –3) правила определения ТЗ суперпозиции (24) можно сформулировать следующим образом. Пусть ТЗ двух пучков ЛГ в суперпозиции (24) равны m и n ( n >  m ). Тогда при отсутствии смещения ( x 0 =0) ТЗ суперпозиции равен n . При любом отличном от нуля смещении ТЗ суперпозиции будет равен TC p , p = 1, 2, 3, 4 из табл. 1. Причем, если m = n , то ТЗ равен TC 1 = n . Если m + n – четное число, то надо смотреть, на сколько изменился максимальный ТЗ n при смещении: n – ( n + m )/2=( n – m )/2. Так как согласно (25–27) ТЗ может уменьшаться только на четное число, то если ( n – m )/2 четное число, то к значению (19) ничего добавлять не надо и ТЗ суперпозиции равен TC 1 =( n + m) /2. Если больший ТЗ n при смещении пучков изменился на нечетное число (( n – m )/2 нечетное), то надо добавить к значению (19) 1, так как согласно (25–27) ТЗ может уменьшаться на четное

Табл. 3. Варианты ТЗ смещенной суперпозиции двух пучков ЛГ и правила выбора нужного варианта

Правила выбора ТЗ суперпозиции	ТЗ всей суперпозиции
n + m четное и ( n – m )/2 четное	TC 1 =( m + n )/ 2
n + m четное и ( n – m )/2 нечетное	TC 2 =( m + n+ 2)/2
n + m нечетное и ( n – m + 1)/2 нечетное	TC 3 =( m + n+ 1)/2
n + m нечетное и ( n – m + 1)/2 четное	TC 4 =( m + n – 1)/ 2

Заключение

В данной работе мы получили нетривиальные правила выбора ТЗ суперпозиции из двух симметрично смещенных пучков ЛГ с номерами (0, n) и (0, m). Прямое применение формулы Берри для расчета ТЗ такой суперпозиции приводит к тому, что ТЗ равен среднему арифметическому (n + m)/2. Понятно, что такой ТЗ может быть полуцелым, чего физически не может быть из-за непрерывности амплитуды светового поля. Поэтому возникает 4 физически возможных варианта ТЗ, которое может быть у суперпозиции: (n + m)/2, (n + m +2)/2, (n + m + 1)/2, (n + m – 1)/2. Чтобы выбрать один из четырех вариантов ТЗ, нужно принять во внимание, что ТЗ несмещенной суперпозиции равен большему ТЗ, например, равен n, если n > m. Численно и с помощью качественного решения трансцендентных уравнений показано, что при смещении двух пучков ЛГ, из бесконечности могут «приходить» четное число оптических вихрей с ТЗ –1, которые будут компенсировать столько же оптических вихрей в суперпозиции с ТЗ +1. То есть ТЗ смещенной суперпозиции по сравнению с ТЗ несмещенной суперпозиции может либо оставаться таким же, либо число. То есть если m + n – четное число, а (n – m)/2 нечетное, то ТЗ суперпозиции равен TC2 =(n + m + 2)/2. Если m + n нечетное число, то согласно (19) ТЗ суперпозиции получается полуцелым, а должен быть целым. Поэтому к ТЗ (19) TC1 = (n + m) /2 следует добавить 1/2 или отнять 1/2. Так как согласно (25 –27) ТЗ суперпозиции может уменьшиться при смещении только на четное число, то надо смотреть на разницу n – (n + m – 1) / 2 = (n – m + 1)/ 2. Если число (n – m + 1) /2, на которое уменьшился больший ТЗ n, четное, то отняли 1/2 правильно и ТЗ суперпозиции равен TC4 =(n + m – 1) /2. А если m + n – нечетное и (n – m + 1) /2 нечетное, то отняли 1/2 от (19) неправильно и надо прибавить к (19) 1/2, то есть ТЗ суперпозиции равен TC3 =(n + m + 1) / 2. Все четыре варианта ответа сведены в табл. 3.

Правильность табл. 3 можно проверить по полученным численно значениям из табл. 2.

уменьшаться на четное число. С учетом этого обстоятельства установлены правила выбора ТЗ из 4 вариантов (табл. 3). ТЗ симметрично смещенных двух пучков ЛГ найден впервые.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в частях «Структурно-устойчивая суперпозиция смещенных гауссовых вихрей», «Суперпозиция двух смещенных с оси пучков ЛГ», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Моделирование».