Суррогатные модели электрофизических характеристик стеклянных деталей высоковольтных изоляторов

V.I. Safonov, ,

V.A. Surin, ,

M.A. Cheskidova, , K.N. Belov, ,

Наличие дефектов в высоковольтных изоляционных конструкциях негативно отражается на их эксплуатационных характеристиках. В связи с этим на этапе производства возникает задача оценки допустимости наличия дефектов с теми или иными параметрами при заранее известных геометрических характеристиках изготавливаемых деталей. Например, для стеклянных деталей высоковольтных изоляторов такого рода оценка проводится на основе требований из [1, 2], не учитывающих точное местоположение дефекта. В то же время в [3] показано значительное различие электрофизических характеристик дефектов одного и того же размера при их различном расположении в стеклянной детали. В связи с этим актуальным является уточнение действующих нормативных требований к дефектам на основе изучения физических процессов, связанных с их появлением. Для этого необходимо получение зависимостей электрофизических характеристик деталей изоляционных конструкций от параметров присутствующих в них дефектов. Такие зависимости могут быть взяты за основу при разработке методик экспресс-оценки допустимости дефектов методами технического зрения, выявленных в процессе производства.

В ряде случаев может возникнуть необходимость изменения геометрических характеристик изоляционных деталей, в частности, при адаптации геометрии существующих изоляторов, работающих при напряжении с частотой 50 Гц, для работы на постоянном напряжении [4]. Зависимости электрофизических характеристик изоляционных деталей от параметров их геометрической формы при наличии дефектов будут полезны при поиске оптимальной формы изоляторов.

В настоящее время для изучения взаимосвязанных физических процессов широко применяется мультифизическое моделирование [5‒7]. Зачас- тую такого рода моделирование требует значительных затрат вычислительных ресурсов и связано с существенными затратами времени. Упрощение сложных моделей за счет включения в их состав готовых зависимостей, описывающих электрическую прочность образцов в зависимости от параметров дефектов, позволит оптимизировать процесс численного моделирования, что скажется на повышении его эффективности.

Детали изоляционных конструкций являются, с точки зрения геометрии, объектами сложной формы. В качестве объекта сложной формы в этом случае можно понимать объект, состоящий из конечного числа простых элементов, ограниченных цилиндрическими и тороидальными поверхностями. Для таких объектов электрофизические характеристики изделий определяются на основе расчета электрических полей методом конечных элементов [8‒10]. При наличии дефектов в изделиях задачу расчета электрического поля часто приходится решать для трехмерных моделей [11]. При этом каждое новое положение дефекта требует проведения повторного расчета, а составление таблиц в зависимости от положения дефекта громоздко и не всегда полноценно описывает ситуацию.

Эффективным инструментом аппроксимации опытных данных являются суррогатные модели [12‒14]. Суррогатные модели строятся либо на основе данных физических экспериментов или результатов численного моделирования на полноценных моделях. Преимуществом использования суррогатных моделей является высокая скорость расчета искомых величин, а недостатком ‒ наличие погрешности расчета по сравнению с расчетом в полных моделях.

Обзор литературы показал, что до настоящего времени суррогатные модели для анализа процессов в изоляторах фактически не применялись. Исключением является суррогатная модель на основе нейронных сетей для расчета электрического поля на поверхности фарфоровых изоляторов воздушных линий электропередачи [15].

Таким образом, целью исследования, описанного в публикации, является разработка подходов к построению суррогатных моделей, описывающих зависимости электрофизических характеристик изоляционных деталей от параметров их сложной геометрической формы, а также присутствующих в них дефектов.

Подходы и методы исследования

Для построения суррогатной модели [16] необходимо определить функциональные зависимости, характеризующие выбранное свойство системы и набор изменяемых характеристик системы, т. е. аргументов этих функциональных зависимостей. Для определяемых функций методом латинского гиперкуба [17, 18] в области изменения аргументов формируется набор значений параметров, для которых необходимо проведение численного или физического эксперимента.

Конечной целью суррогатной модели является определение потенциального изменения электрической прочности образца при наличии дефектов в образце [3]. Поэтому в качестве набора функций можно ограничиться максимальной и минимальной напряженностью электрического поля E_max, E_min^в области расположения дефекта. Также полезной является средняя напряженность электрического поля E_av в дефекте. Указанные функциональные зависимости E_max , E_min и E_av будут рассматриваться далее в рамках исследования.

Дефекты прозрачных объектов сложной формы достаточно разнообразны. Наличие дефекта может быть связано с нарушением формы внешней поверхности (царапины, сколы, кованность [1]). Если геометрические размеры дефекта сопоставимы с размерами элементов объекта, можно говорить о существенном изменении формы объекта. Такого рода дефекты слабо поддаются обобщению при помощи конечного числа параметров и требуют подробного изучения в каждом конкретном случае. В случае, когда наличие дефекта не приводит к нарушению целостности поверхности объекта, говорят о наличии внутренних дефектов (газовые включения, твердые включения, посечки). Поверхностные дефекты, уступающие по размерам элементам, могут быть рассмотрены как частный случай внутренних дефектов при соответствующем изменении их расположения. Однако при этом искомые электрофизические характеристики будут резко отличаться по отношению к случаю внутренних дефектов. В целях упрощения разрабатываемой модели целесообразно ограничиться рассмотрением внутренних дефектов.

Дефекты внутри изоляционной детали могут иметь различную геометрическую форму. С целью сокращения числа параметров, описывающих фор- му дефекта, целесообразно ограничиться дефектами в виде эллипсоидов с осями а, b и с. Такое допущение справедливо для случаев газовых и твердых включений. Физические свойства материалов изолятора и дефекта определяются диэлектрической проницаемостью £о и удельной проводимостью уо для изолятора и аналогичными величинами £д и уд - для дефекта.

Исходя из [3, 19] можно утверждать, что наличие дефектов оказывает влияние на картину электрического поля внутри ограниченной области пространства вокруг дефекта. Поэтому при составлении имитационной модели можно ограничиться областью объекта, непосредственно прилегающей к дефекту.

Для деталей с осевой симметрией будем рассматривать сегмент, показанный на рис. 1. Расстояние от оси до центра дефекта обозначено R. Внутренняя (слева) и внешняя (справа) границы области имеют сложную форму, образованную вращением вокруг оси соответствующих кривых. Внутреннюю и внешнюю границу можно описать в виде периодической функции одной переменной и задать рядом Фурье. Периоды функций, описывающих внешнюю и внутреннюю границы, равны Т и Т₂ соответственно. Постоянные составляющие этих функций - R i и R₂, амплитуды гармоник - А(_к) и В(_к), начальные фазы гармоник - у(_к) и ^(_к) . Дефект будем считать неподвижным, а изменение его расположения будет полностью описываться параметрами R, Т_ъ Т 2 , R_b R 2 , А₍ к) , В (к), ^(к) и ^ (к) .

Параметры, описывающие материалы £_о, у_о, £_д, у_д, форму дефекта а, b, с и его расположение и форму объекта R, Т, Т 2 , R i , R2, А(к), В (к), ^(к) и Ф(_к), будут аргументами в рассматриваемой суррогатной модели. В зависимости от конкретной задачи, на решение которой направлена суррогатная модель, количество параметров может быть сокращено. Например, при разработке методик экспресс-оценки допустимости дефектов при производстве конкретного изолятора можно не рассматривать параметры, описывающие границы объекта.

Картина электрического поля в модели на рис. 1 полностью определяется законами распределения потенциалов вдоль внутренней и внешней границ, а также законами изменения их во времени. На практике размеры внутренних дефектов уступают размерам элементов внешних границ изоляционной детали, что позволяет считать потенциалы на границе зависящими только от времени. В силу ярко выраженных диэлектрических свойств изоляционной детали можно пренебречь вихревыми составляющими электрического поля и проводить расчет картин поля при квазистационар-ной формулировке задачи в частотной области [20]. Потенциал внешней границы считаем равным нулю, потенциал внутренней границы – синусоидальной функцией с амплитудой U и частотой f.

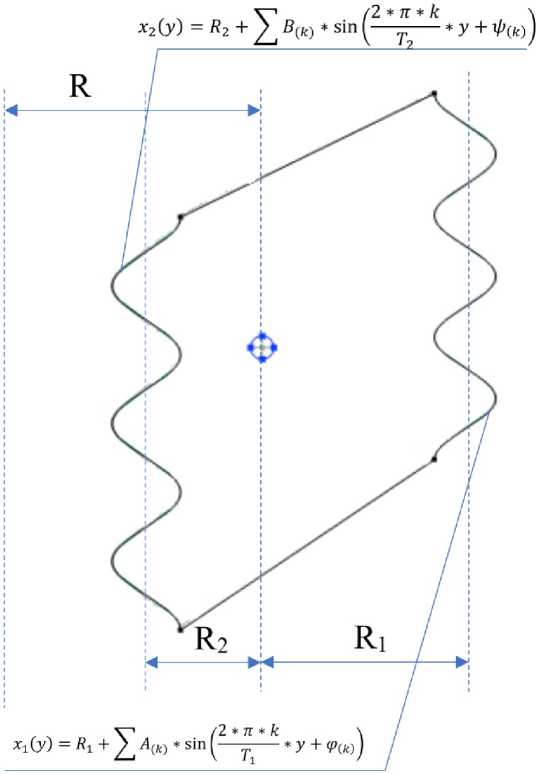
Рис. 1. Осевое сечение области объекта сложной формы с дефектом

Fig. 1. The axial section of the area of an object of complex shape with a defect

Суррогатные модели могут быть построены на основе нейронных сетей [21], процесса Гауссовой регрессии [22], радиальных базисных функций [23], полиномов нескольких переменных натуральной степени [24] и др. Выбор типа суррогатной модели определяется количеством независимых параметров и видом аппроксимирующих функций, наиболее подходящих для описания полученных опытных данных с минимальной погрешностью.

Далее рассмотрим особенности построения суррогатной модели для системы технического зрения, осуществляющей анализ дефектов в изоляторе ПС-70Е. На рис. 2 слева представлена внутренняя граница стеклянной детали со стороны стержня, справа ‒ внешняя граница со стороны шапки. В этом случае положение газового включения определяется параметрами d и г. Переменная d характеризует расположение центра включения над плоскостью 2 = 0, параметр г - удаленность центра дефекта от оси вращения. Параметр г меняется в пределах от 2 до 11,2 мм. Диапазон выбран таким образом, чтобы обеспечить расположение газового включения внутри стеклянной детали и учесть случаи максимального приближения газового включения к границам модели. Величина d изменяется от 0 до 10 мм, что укладывается в период повторяемости внутренней поверхности.

Геометрия газового включения описывается в виде эллипсоида с полуосями а, b и с, расположенными параллельно координатным осям X, Y и Z. Каждый из указанных параметров меняется в диапазоне от 0,1 до 1 мм, что соответствует допустимому диапазону размеров газового включения в головке стеклянной детали согласно [1]. Параметры материалов в модели аналогичны принятым в [3].

Таким образом, для экспресс-диагностики суррогатная модель содержит 5 независимых параметров и имеет вид:

Етах = f!(a,b,c,r,d);

Е_т[п= f₂⁽a,b,c,r,d) (1)

E_av = f₃(a,b,c,r,d').

В силу линейности свойств материалов рассматриваемой модели можно условно принять потенциал внутренней границы U = 1 В. При этом можно говорить об относительной напряженности электрического поля, измеряемой в 1/м. Частота приложенного напряжения f = 50 Гц.

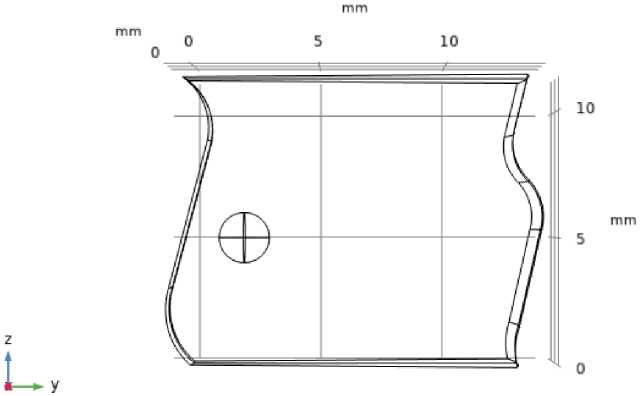
Рис. 2. Полная модель элемента стеклянной детали изолятора ПС-70Е Fig. 2. Full model of the element of the glass part of the insulator PS-70E (U70)

Результаты расчета погрешностей суррогатных моделей в виде полиномов Results of error estimation for surrogate models in the form of polynomials

Степень полинома	Максимальная погрешность, %			Модальная погрешность, %
	max	min	av	max	min	Eav
3	44,1	24,0	35,3	2,2	1,7	0,6
4	26,8	14,1	15,1	1,6	1,4	0,2
5	18,5	12,0	8,3	0,4	1,6	0,2
6	14,7	9,3	5,2	0,4	1,0	0,1
7	9,1	9,3	4,7	0,5	0,7	0,0

На основании известных законов электротехники можно утверждать, что напряженности электрического поля будут непрерывными функциями аргументов, перечисленных в (1). Это позволило для их аппроксимации выбрать полиноминальную зависимость:

E(a,b,c,r,d) =

= ^=oT^₊t₊u+v+w=i^            . (2)

Здесь n - степень полинома; P_stuvw - коэффициенты, вычисляемые методом наименьших квадратов. Во внутренней сумме участвуют слагаемые со всеми возможными комбинациями показателей степеней, подчиняющихся условию s + t + u + v + w = i. Выбор зависимости (2) существенно упростил построение суррогатной модели.

Для построения модели с необходимой относительной погрешностью не более 10 % необходимо было выбрать оптимальную степень полинома. Для этого был организован следующий итерационный процесс по увеличению степени полинома и количества экспериментальных точек. Для заданной степени полинома количество экспериментальных точек увеличивалось до тех пор, пока наблюдалось существенное снижение погрешности. Методом латинского гиперкуба вычислялся набор параметров, имитационное моделирование для которых необходимо для определения всех коэффициентов полинома. Полученные точки оптимизи- ровались согласно метрике Centered discrepancy. Коэффициенты при слагаемых полинома рассчитывались методом наименьших квадратов. Проверка погрешности модели выполнялась для каждой точки гиперкуба путем сравнения напряженности поля согласно результатам численного эксперимента и напряженности поля по суррогатной модели.

Результаты расчета максимальной и модальной погрешностей для полиномов представлены в таблице. Во всех случаях минимальная погрешность примерно равна нулю.

Результаты, представленные в таблице, получены для гиперкуба с 10 000 точками. Установлено, что при данном количестве точек погрешности полинома 7-й степени достигают приемлемой инженерной точности менее 10 %. Для полиномов низшего порядка и для полинома 7-го порядка, но с меньшим количеством экспериментальных точек, достичь требуемой точности не удалось.

Результаты и их обсуждение

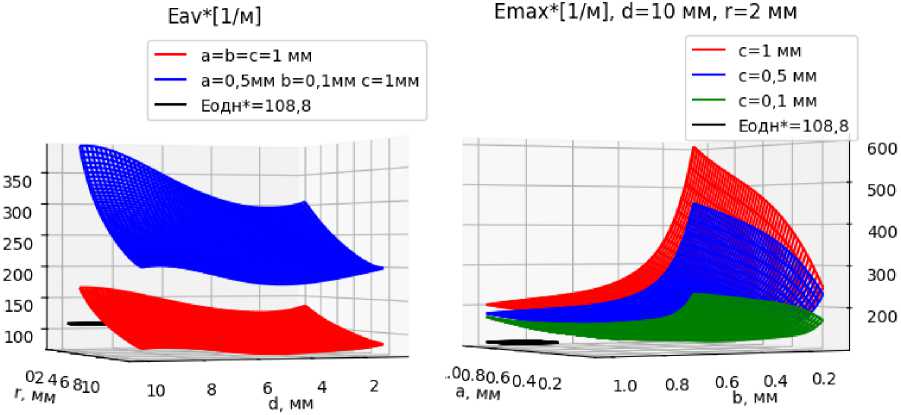
С использованием полученной суррогатной модели построены зависимости напряженностей электрического поля внутри газового включения. На рис. 3а показаны зависимости средней напряженности при изменении параметров d и г.

На рис. 3а рассмотрено два случая: сферическое включение диаметром 2 мм (а = b = c = 1 мм ) и

а)

b)

Рис. 3. Зависимости напряженности электрического поля от параметров суррогатной модели

Fig. 3. Dependences of the electric field strength on the defect parameters obtained on the basis of a surrogate model

включение в виде эллипсоида, вытянутое вдоль оси, перпендикулярной градиенту потенциала поля (а = 0,5 мм; b = 0,1 мм; с = 1 мм ). Для обоих случаев видно, что наибольшие значения напряженности поля ожидаются при значениях параметров d = 10 мм; г = 2 мм. Для указанных параметров на рис. 3b построены зависимости максимальной напряженности поля при различных размерах полуосей эллиптического газового включения. Из рис. 3b видно, что наибольшее значение напряженности ожидается при сочетании параметров а = 1 мм; b = 0,1 мм; с = 1 мм, что соответствует газовому включению, сжатому вдоль градиента поля и вытянутому по остальным осям.

Среднее расстояние между внешней и внутренней границами модели на рис. 2 составляет 12,87 мм. При этом в случае нахождения дефекта во внешнем плоскопараллельном поле напряженность однородного поля внутри сферического включения E_ogHt = 108,8 м^-1 [19]. На рис. 3 это показано в виде участка плоскости. Сравнение данного значения с полученными результатами показывает, что отклонение максимальной напряженности поля от данного значения не более 1 % наблюдается для сферического включения в диапазоне изменения параметра г от 6 до 9 мм, что соответствует удалению газового включения от внутренней границы большему, чем на половину толщины стеклянной детали. Для средней и минимальной напряженности данные диапазоны составляют от 4 до 7 мм и от 3,5 до 6 мм.

Рассмотренный выше метод получения суррогатных моделей можно применять для экспресс-оценки с помощью технического зрения допустимости дефектов в изоляционных деталях сложной формы. Анализ, выполняемый при помощи суррогатных моделей, позволяет определять области с наибольшими значениями напряженности поля, что позволит системе технического зрения выявлять наиболее опасные дефекты.

Описанные полиномиальные модели могут быть применены в составе мульфизических моделей в случаях, когда не требуется изучения влияния геометрии изоляционной детали. В рамках задач по проектированию изоляционных деталей с измененной геометрией полиномиальные модели могут быть применены, если будут зафиксированы параметры дефекта и будет рассматриваться изменение параметров поверхности детали.

Использование полиномиальной суррогатной модели обладает определенными преимуществами. Прежде всего это детерминированный характер алгоритма создания модели. Это позволяет избежать сложностей [25] с выбором оптимального количества слоев нейронной сети и количества элементов в каждом слое.

Основными факторами, определившими предпочтительное использование полиномиальной модели в рассматриваемом случае, были скорость определения имитационных данных и близость изучаемой зависимости к полиному достаточно низкой степени.

Полиномиальные суррогатные модели содержат относительно небольшое число слагаемых при малом числе свободных параметров. Например, рассмотренные полиномы 5 переменных 7-й степени содержат 792 слагаемых. Увеличение числа свободных параметров или степени полинома приведет к соответствующему увеличению числа слагаемых. Применение метода наименьших квадратов для определения коэффициентов таких полиномов требует соответствующего увеличения числа опытных точек, что снижает скорость обучения моделей и скорость их вычислений.

Для ряда моделей ресурсы, затрачиваемые на получение результата путем имитационного и (или) физического моделирования, могут быть достаточно большими. В рассмотренном случае моделирования дефектов в изоляционной детали удалось составить достаточно простую физическую модель с высокой скоростью сходимости, в которой рассчитывалось электрическое поле только вблизи дефекта. В этом случае время расчета одной точки составляло несколько секунд, что позволило рассчитать необходимое количество опытных точек для обучения полиноминальной суррогатной модели.

В общем случае вопрос об определении границ целесообразного применения полиноминальных суррогатных моделей по отношению к моделям других видов – нейронным сетям, Гауссовой регрессии и т. д. – остается открытым. Однако сформулированные выше оценочные критерии помогают выбрать более оптимальный вариант суррогатной модели.

Заключение

Рассмотрен один из возможных подходов получения суррогатных моделей для расчета электрофизических характеристик изоляционных дета- лей сложной формы от параметров их геометрии, а также присутствующих дефектов. Определены способы формирования наиболее оптимальной физической модели для получения имитационных данных, необходимых при обучении суррогатной модели. Также определены наиболее целесообразные функциональные зависимости для оценки электрической прочности образца и принципы подбора аргументов этих функциональных зависимостей.

На примере стеклянной детали изолятора ПС-70Е с газовым включением показано получение суррогатных моделей в виде полиномов 5 переменных 7-й степени. Полученную суррогатную модель можно использовать в системе технического зрения для экспресс-диагностики допустимости дефектов и определения характерных областей, в которых могут быть дефекты с наибольшей напряженностью электрического поля. Использование суррогатной модели в системе технического зрения обеспечивает большую скорость принятия решений. На основании того, что относительная погрешность полученной суррогатной модели не более 10 %, сделан вывод о возможности решения задач экспресс-диагностики с использованием полиномиальных суррогатных моделей.