Survey of Sparse Adaptive Filters for Acoustic Echo Cancellation

• I.    Introduction

  Echo cancellation in telecommunication network requires identification of unknown echo path impulse response. The length of network echo path is typically in the range between 32 and 128 milliseconds, which is characterized by bulk delay depending on network loading, encoding and jitter delay [1]. Because of this, “active” region of echo path is in the range between 8 and 12 milliseconds, so it contains mainly “inactive” components where the coefficient magnitudes are close to zero, making the impulse response more sparse. In general, adaptive filters have been used to estimate the unknown echo path by using algorithm such as normalized least-mean-square NLMS. But, as the length of echo paths are more, NLMS requires more number of taps (up to 1024 taps) which will make the convergence of NLMS becomes poor.

Several approaches have been proposed over recent years to get better performance than NLMS for Network echo cancellation (NEC). These include Variable step size (VSS) algorithms,[2] [3] [4] partial update adaptive filtering techniques[5][6] and sub-band adaptive filtering (SAF) techniques.[7] These approaches aim to address the issues in echo cancellation including the performance with colored input signals and time varying echo paths and a computational complexity to name but a few. In contrast to these algorithms, sparse adaptive algorithms have been developed to address the performance of adaptive filters sparse system identification.

The first sparse adaptive algorithm for (NEC) is proportionate normalized least-mean-square (PNLMS)[8] in which each filter coefficient is updated independently of others, by adjusting the adaptation step size in proportion to the estimated filter coefficient. It is known that PNLMS has fast initial convergence rate.

This paper is organized as follows, in section II explains about the echo cancellation process by using recent algorithms. Section III explains about the acoustic impulse response and section IV gives about adaptive echo cancellation methods, Section V and VI gives the information about Sparse Adaptive filters and their algorithms respectively, Sections VII,VIII, IX explains about existing sparse adaptive filters, sparseness measure and sparse impulse response generator and the section X gives the comparative analysis and their performance of sparse adaptive filter algorithms and this paper is summarized and concluded in section X.

• II.    ECHO CANCELLATION

Among the wide range of adaptive filtering applications, echo cancellation is likely the most interesting and challenging one. The original idea of this application appeared in the sixties [9], and it can be considered as a real milestone in telecommunication systems. A general scheme for echo cancellation is depicted in Figure.1. In both network and acoustic echo cancellation contexts [10] it is interesting to notice that the scheme from Figure.1 can be interpreted as a combination of two classes of adaptive system configurations, according to the adaptive filter theory [11]. First, it represents a “system identification” configuration because the goal is to identify an unknown system (i.e., the echo path) with its output corrupted by an apparently “undesired” signal (i.e., the near-end signal). But it also can be viewed as an “interference cancelling” configuration, aiming to recover a “useful” signal (i.e., the near-end signal) corrupted by an undesired perturbation (i.e., the echo signal); consequently, the “useful” signal should be recovered from the error signal of the adaptive filter.

Each of the previously addressed problems implies some special requirements for the adaptive algorithms used for echo cancellation. Summarizing, the “ideal” algorithms should have a high convergence rate and good tracking capabilities (in order to deal with the high length and time varying nature of the echo path impulse responses) but achieving low mis adjustment.

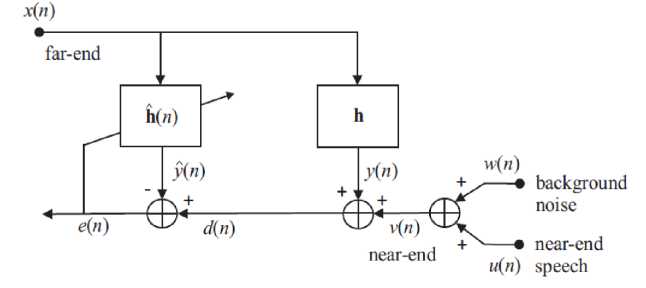
Figure 1 : General Configuration of Echo Cancellation

These issues should be obtained despite the non-stationary character of the input signal (i.e.,speech). Also, these algorithms should be robust against the near-end signal variations, e.g., background noise variations and double talk. Finally, its computational complexity should be moderate, providing both efficient and low cost realtime implementation. Even if the literature of adaptive filters contains a lot of very interesting and useful algorithms [12], there is not an adaptive algorithm that satisfies all the previous requirements.

Different types of adaptive filters have been involved in the context of echo cancellation. One of the most popular is the normalized least-mean-square (NLMS) algorithm. Also, the affine projection algorithm (APA) [originally proposed in (12)] and some of its versions, e.g., [13], [14], were found to be very attractive choices for echo cancellation. However, there is still a need to improve the performance of these algorithms for echo cancellation. More importantly, it is necessary to find some way to increase the convergence rate and tracking of the algorithms since it is known that the performance of both NLMS and APA are limited for high length adaptive filters.

• III.    ACOUSTIC IMPULSE RESPONSE (AIR)

When a sound is generated in a room, the listener will first hear the sound via the direct path from the source. Shortly after, the listener will hear the reflections of the sound off the walls which will be attenuated, as shown in Figure 2.

Each reflection will then in turn be further delayed and attenuated as the sound is reflected again and again off the walls. Further examination of the impulse response of a room yields the observation that the sound decays at an exponential rate. Therefore, the impulse response of the room shown above may be similar to Figure 3.

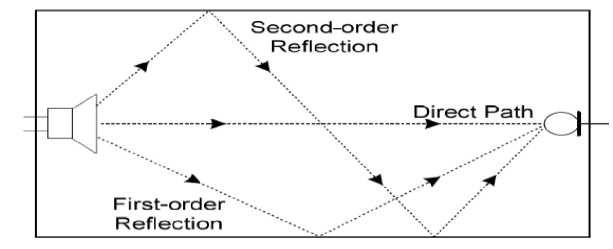
Figure 2 : A Visual Example of how sound propagates through room

The echoes effects can be reduced by having absorbers around the wall. In the case, the impulse response has less active coefficients, as depicted in Figure 4. The latter impulse response is said to be more sparse system than the former, due to the majority of its filter taps are inactive.

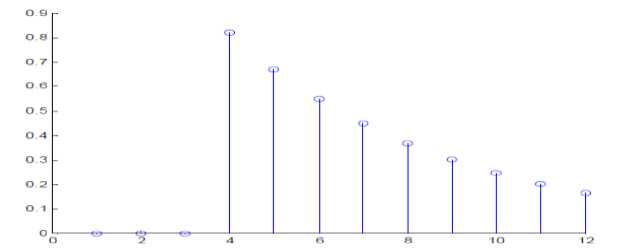
Figure 3 : Impulse response of the room shown in Figure 2

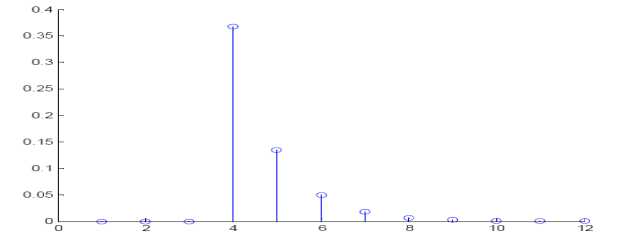
Figure 4 : Sparse impulse response of the room in the presence of echo absorbers

• IV.    THE ADAPTIVE ECHO CANCELLATION PROCESS

Figure 5: shows an acoustic echo canceller set-up by employing an adaptive filter.

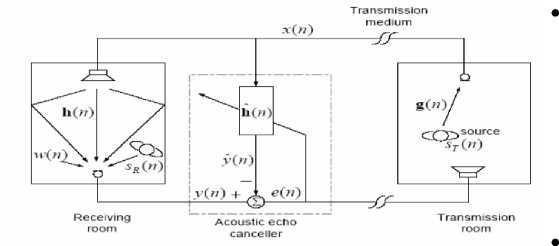
Figure 5 : Single Channel Echo Cancellation

In this paper, [ ]T denotes matrix transpose and E[ ] signifies mathematical expectation operator. Scalars are also indicated in plain lowercase, vectors in bold lowercase and matrices in bold uppercase.

The length of h (n), L r is same as the length of h (n), L. In a reality, the length of the adaptive filter is less than the receiving room impulse responses. This is due to the fact that the computational complexity of an adaptive algorithm increases monotonically with the length of the adaptive filter. Therefore, L must be long enough to achieve a low system mismatch and computational complexity.

There is no noise signal in the receiving room, w (n) = 0

There is no source signal in the receiving room, S R (n) = 0, i.e., no doubletalk is present.

A transversal finite impulse response (FIR) filter configuration is used, as shown in figure 6, due to its stability characteristics.

Notations and definitions:

• g (n) = impulse response of transmission room

= [g 0 (n) g 1 (n) g 2 (n) ……g Lt-1 (n)]^T Where L t is the length of g (n)

h (n) = impulse response of receiving room

= [h 0 (n) h 1 (n) h 2 (n) ……h Lr-1 (n)]^T Where L r is the length of h (n)

h (n)= impulse response of adaptive filter

= [h^{^} 0 (n) h^{^} 1 (n) h^{^} 2 (n) …… h^{^} L-1 (n)]^T Where L is the length of h (n)

x (n) = input signal to the adaptive filter and the receiving room system

= [x(n) x(n-1) ... x(n-L+1)]T

S T (n) = transmission room source signal

S R (n) = Receiving room source signal

w (n) = Noise signal in Receiving room

The receiver attached in the transmission room (right hand side in figure (2) picks up the a time varying signal x (n) from a speech source S_T(n) (far-end speaker) via impulse response of the transmission room g(n). The input signal x (n) is then transmitted to the loudspeaker in the near-end receiving room. The receiving room's microphone receives the desired signal y(n) which is the convoluted sum of the input signal and the impulse response of the receiving room h (n) along with near-end speech signal and some additive noise. Therefore,

y(n) = h ^T(n) x (n) + w(n) + S r (h)                       (1)

In absence of echo canceller, the received signal y(n) will be transmitted back to the origin with some delay. In the presence of an adaptive echo canceller, its objective is to estimate h(n) by taking into account the error signal e(n) at each iteration, where the e(n) is defined as e (n) = Output from the receiver room system- output from the adaptive filter

=y(n)-y^(n)                                   (2)

= [ h ^T (n)- h ¹ (n)] x (n)+w(n)+S R (n)

• • For effective echo cancellation, e(n) must be significantly smaller in each iteration, as the filter coefficients converges to the unknown true impulse response h(n). Several adaptive algorithms are available for the weighs update and they generally exchange increased complexity for improved performance.

Therefore Echo cancellers can be potentially employed in telecommunication systems so that the undesired echoes, both acoustic and hybrid, can be diminished.

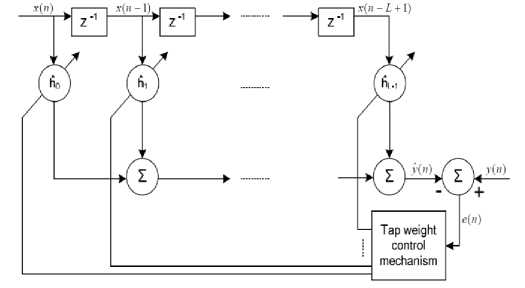
Figure 6 : Adaptive transversal FIR Filter

• V.    SPARSE ADAPTIVE FILTERS

The main goal in echo cancellation is to identify an unknown system, i.e., the echo path, providing at the output of the adaptive filter a replica of the echo. Nevertheless, the echo paths (for both network and acoustic echo cancellation scenarios) have a specific property, which can be used in order to help the adaptation process. The sparseness of an acoustic impulse response[15] is more problematic because it depends on many factors, e.g., reverberation time, the distance between loudspeaker and microphone, different changes in the environment (e.g., temperature or pressure), however, the acoustic echo paths are in general less sparse as compared to their network counterparts, but their sparseness can also be exploited.

Even if the idea of exploiting the sparseness character of the systems has appeared in the nineties, e.g.,[16],[17], [18], the proportionate NLMS (PNLMS) algorithm[19] proposed by Duttweiler a decade ago, was one of the first“true”proportionate-type algorithms and maybe the most referred one. As compared to its predecessors, the update rule of the PNLMS algorithm is based only on the current adaptive filter estimate, requiring no a priori information about the echo path. However, the PNLMS algorithm was developed in an “intuitively” manner, because the equations used to calculate the step-size control factors are not based on any optimization criteria but are designed in an ad-hoc way. For this reason, after an initial fast convergence phase, the convergence rate of the PNLMS algorithm significantly slows down. Besides, it is sensitive to the sparseness degree of the system, i.e., the convergence rate is reduced when the echo paths are not very sparse. In order to deal with these problems, many proportionate-type algorithms were developed in the last decade. The overall goal of this paper is to present and analyse the most important sparse adaptive filters, in order to outline their capabilities and performances in the context of echo cancellation. In view of this paper reviews the basic proportionate-type NLMS adaptive filters, the classical PNLMS [19], the improved PNLMS [20], and other related algorithms are discussed. The exponentiated gradient (EG) algorithms [21] and their connections with the basic sparse adaptive filters are presented. Some of the most recent developments in the field, including the mu-law [22], [23] and other new PNLMS-type algorithms are also included. A variable step-size PNLMS-type algorithm is also analysed for aiming to better compromise between the conflicting requirements of fast convergence and low maladjustments encountered in the classical versions. Which further improve the performance of the PNLMS-type algorithms.

An impulse response can be considered “sparse” if a large fraction of its energy is concentrated in a small fraction of its duration. Adaptive system identification is a particularly challenging problem for sparse systems. [36] An application of sparse system identification which is of current interest is packet-switched network echo cancellation. The increasing popularity of packet-switched telephony has led to a need for the integration of older analog systems with, for example, IP or ATM networks. Network gateways enable the interconnection of such networks and provide echo cancellation. In such systems, the hybrid echo response is delayed by an unknown bulk delay due to propagation through the network. The overall effect is therefore that an “active” region associated with the true hybrid echo response occurs with an unknown delay within an overall response window that has to be sufficiently long to accommodate the worst case bulk delay.

In the context of Networking and acoustic echo cancellation the convergence performance, computational complexity of the existing sparse adaptive filters and the performance of sparseness measure of improvement is analysed .Finally the recent algorithms of sparse adaptive filters which were mentioned in the comparison table.1 are discussed. It has been observed that the proposed algorithms Sparseness controlled µ-Law Proportionate NLMS (SC-MPNLMS) and Sparseness controlled-Improved Proportionate NLMS (SC-IPNLMS)[32]are robust to variations in the level of sparseness in AIR with only a modest increase in computational complexity.

• VI.    SPARSE ADAPTIVE FILTER ALGORITHMS

A sparse impulse response has most of its components with small or zero magnitude and can be found in telephone networks. Due to the presence of bulk delays in the path only 8-10% exhibits an active region. Figure.7 shows a typical sparse impulse response, which can be realized in reality.

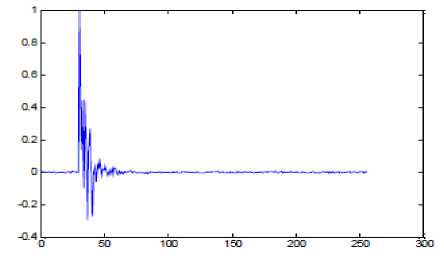
Figure 7 : An example of a sparse impulse response exists in telephone networks.

The NLMS algorithm does not take into account this feature when it presents in a system and therefore performs inadequately. This is because [24].

• •    The need to adapt a relatively long filter

• •    The unavoidable adaptation noise occur at the inactive region of the tap weights

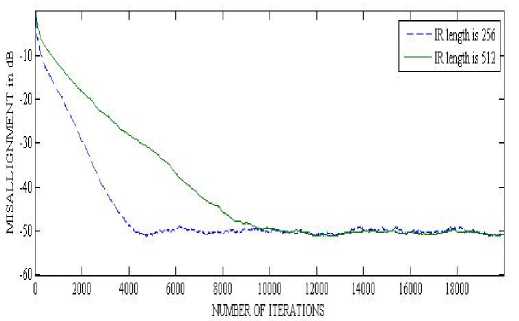
Figure 8 : Convergence of NLMS when Filter Length changes from 256 to 512.

While in the NLMS, the adaptation step is same for all components of the filter, in the sparse algorithms, such as PNLMS, IPNLMS and MPNLMS, adaptive step sizes are calculated from the last estimate of the filter coefficients in an efficient way that the step size is proportional to the size of the filter coefficients. This is resulted to adjust the active coefficients faster than the non-active ones. Therefore, the overall convergence time is reduced.

• VII.    EXISTING SPARSE ADAPTIVE FILTER ALGORITHMS

The method of steepest descent avoids the direct matrix inversion inherent in the Wiener [15].This paper gives the in detailed information by studying the most common approach to adaptive filtering, the stochastic gradient based algorithms. And several modifications to this algorithm, are made in order to cope with practical constraints, and are discussed in. Since a wide variety of algorithms are available in the survey, this paper defines and analyses the existing sparse adaptive filter and their performances using simulation results [36] of their different subjective measures and computational requirements. Stochastic gradient based algorithms do not provide an exact solution to the problem of minimizing the MSE as the steepest descent approach, rather approximates the solution. However, the requirement for stationary input or knowledge of autocorrelation matrix, and the cross-correlation vector, in steepest descent approach are circumvented in the algorithms [15].

This type of algorithms are widely used in various applications of adaptive filtering due to its low computational simplicity, proof of convergence in the stationary environment, unbiased convergence in the mean to the Wiener solution and stable behavior in the finite-precision arithmetic implementations .

While in the NLMS, the adaptation step is same for all components of the filter, in the sparse algorithms, such as PNLMS, IPNLMS and MPNLMS, adaptive step sizes are calculated from the last estimate of the filter coefficients in an efficient way that the step size is proportional to the size of the filter coefficients. This is resulted to adjust the active coefficients faster than the non-active ones. Therefore, the overall convergence time is reduced.

• VIII.    SPARSNESS MEASURE

Degree of sparseness can be qualitatively referred as a range of strongly dispersive to strongly sparse. Quantitatively, the sparseness of an impulse response can be measured by the following sparseness measure.

Where

^(h )=_L_ [i -  I'(n)L

L - VZ [   ZT^h (n )|2

Ih (n *=zi h (n )i l=0

II h ( n ) =л/у L=1 h 2( n)

2 V Z -01 = 0 '

• IX.    SPARSE IMPULSE RESPONSE GENERATOR

Sparseness of impulse responses for Network and acoustic echo cancellation can be studied by generating synthetic impulses using random sequences. This can be achieved by first defining an L×1 vector uixi =kxi   1  e-1/"   e—2 "...... e^Lu —1) " ]"  (4)

Where the leading zeros with length Lp models the length of the bulk delay and Lu = L – Lp is the length of the decaying window which can be controlled by ψ. Smaller the ψ value yields more sparse system.

Defining a Lu × 1 vector b as a zero mean white Gaussian noise (WGN) sequence with variance σ b ², the L × 1 synthetic impulse response can then be expressed as

BL„ - Z = diag{b},

h ( n )

^LP ^{x L}P

L u ^{X L}p

⁰ L p - L u

B

Lu -Lpu u + p

Where the L × 1 vector p ensures elements in the ‘inactive’ region are small but non-zero and is an independent zero means WGN sequence with variance σ p ²

Figure 2.shows two impulse responses that can be attained using this approach, by setting the impulse length L =512, the bulk delay length L p =32 and ψ to 8(more sparse), 20, 50 and 100(more sparse).

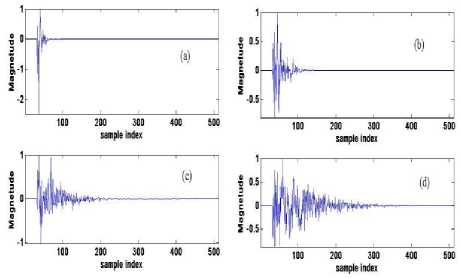
Figure 9 : Impulse responses controlled using (a) ψ = 8, (b) ψ = 20, (c) ψ =50 and (d) ψ =80 giving sparseness measure (a) ξ = 0.905,(b) ξ = 0.809, (c) ξ = 0.667 and (d) ξ = 0.

• X.    Comparison of sparse adaptive filter methods

The details of the sparse adaptive filters models are given in the Table I.

TABLE I: Analysis of different sparse adaptive filter methods

Sl. No	Paper Title	Proposed Models	Performance	Remarks
1	Adaptive Filtering Algorithms for promoting Sparsity [25]	A steepest descent algorithm (SDA) Is developed to minimize the regularized cost function. Then extended the algorithm to the adaptive environment and developed a class of algorithms such as - pLMS, pLLMS and pNLMS.	The algorithms are based on minimizing the mean squared error regularized by a ^fp diversity measure with the developed both SDA-type algorithms and adaptive algorithms. In this paper mathematical framework is quite general since it encompasses a broad range of adaptive algorithms- PNLMS, LMS, LLMS and NLMS.	This paper mainly focused on the pLMS, pLLMS and pNLMS acoustic model exploring the advantages of these algorithms.
2	Sparseness Controlled Adaptive Tap Algorithms for Partial Update Adaptive Filters[26]	Here in this paper the authors proposed a partial update strategy which adapts not only the filter coefficients but also the number of taps to be updated. A novel adaptive tap partial update algorithm, Sparseness-Controlled Adaptive Tap IPNLMS-MMAX (SCAT IPNLMS-MMAX), is proposed which incorporates a new measure for sparseness.	With the proposed method for adaptively changing the number of partially updated taps using a new sparseness measure of an adaptive filter. The convergence process has been analysed and the method of having two convergence stages with different partial update criteria has been used to construct a novel adaptive tap partial update algorithm, SC-AT IPNLMS-MMAX. The simulation results show that that for SC-AT IPNLMS-MMAX, faster convergence speed is obtained with less computation than with the fully updated IPNLMS and SC-IPNLMS.	This paper focused on computationally efficient sparseness representations as well as on the development of low power architectures for the proposed algorithm.
3	Adaptive Combination of Proportionate Filters for Sparse Echo Cancellation[27]	In this paper, it has given on observed that how combination schemes, where the outputs of two independent adaptive filters are adaptively mixed together, can be used to increase IPNLMS robustness to channels with different degrees of scarcity, as well as to alleviate the rate of convergence vs steady-state misadjustment tradeoff imposed by the selection of the step size.	This paper it has shown how combination schemes can help to improve the performance of proportionate filters, by alleviating the speed vs precision tradeoff, as well as by increasing robustness to channels with different degrees of sparsity.
4	Adaptive algorithms for sparse echo cancellation[28]	In this paper An efficient low cost implementation of our new algorithm using partial update adaptation is presented and evaluated.	This algorithm exploits both sparseness of the echo response and also sparseness of the input signal in order to achieve high performance without high computational cost.	Determining an optimal function for this relationship is an interesting topic of ongoing work.
5	Adaptive algorithms for acoustic echo cancellation in speech processing[29]	This paper focuses on the use of LMS and NLMS algorithms to reduce this unwanted echo, thus increasing communication quality.	The performance of NLMS algorithm is having the advantage over the LMS algorithm in case of Mean square error and Average attenuation.	By distinguishing LMS and NLMS the computational complexity more for NLMS.
6	Sparse Signal Processing Using iterative Method with Adaptive Thresholding (IMA T)[30]	In this paper it is presented that random sampling performs as good as or better than compressive sampling. In addition, we show that greedy methods such as Orthogonal Matching Pursuit (OMP) are   too   complex   with   inferior performance compared to IMAT and other iterative methods. Furthermore, we shall compare IMAT to OMP and other reconstruction methods in term of complexity and show the advantages of IMAT.	A parameter selection rule for optimal steadystate performance is proposed. And The steadystate MSD gain is obtained theoretically of ^) -LMS over the tradition algorithm, with this optimal parameter.
7	Performance Analysis of Ɩ 0 Norm Constraint Least Mean Square Algorithm[31]	This paper presents comprehensive theoretical performance analysis of -MS for white Gaussian input data.	The proposed algorithms ( SC-PNLMS and SC-MPNLMS) achieve the improvement with only a modest increase in computational complexity. Authors presented a class of sparseness-controlled algorithms which achieves improved convergence compared to classical NLMS and typical sparse adaptive filtering algorithms.	All the three transient items in MSD convergence of^) -LMS has faster attenuation rate than LMS, leading to acceleration of the convergence rate.

8	A Class of Sparseness-controlled Algorithms for Echo Cancellation[32]	Here it is represented that to propose a class of AEC algorithms that can not only work well in both sparse and dispersive circumstances, but also adapt dynamically to the level of sparseness using a new sparseness-controlled approach.	this proposed algorithm had the least steady state maladjustment, and also could converged the most quickly.	These proposed algorithms have same or faster convergence in NEC. and shows improved Performance over existing methods in the context of computational complexity.
9	A New Variable Step Size LMS Adaptive Filtering Algorithm[33]	Focus on the inconsistency between the convergence rate and the steady state error in LMS algorithm, this paper proposed a new variable step size LMS (VSS-LMS) algorithm, by constructing a nonlinear function between the step factor µ and the error signal e (n).	The proposed algorithm achieves faster convergence, outperforming the IAF-PNLMS and other well-known PNLMS-type algorithms. Convergence speed is significantly improved the MPNLMS and EIAF-PNLMS algorithms exhibit similar performance for weakly correlated input signals.	This     algorithm    took advantage both in convergence rate and steady state maladjustment with other variable size step LMS algorithms.
10	An Enhanced IAF-PNLMS Adaptive Algorithm for Sparse Impulse Response Identification[34]	This paper presents an individualactivation-factor proportionate normalized least-mean-square (IAF-PNLMS) algorithm that (during the adaptive process) uses a new gain distribution strategy for updating the filter coefficients.	The proposed SC-PNLMS algorithm takes into account the sparseness measure via the coefficient update function.	The proposed algorithm slightly outperforms the AMPNLMS for highly correlated input data.
11	A sparseness controlled proportionate algorithm for acoustic Echo cancellation[35]	The proposed sparseness-controlled PNLMS (SC-PNLMS) algorithm inherits the beneficial properties of both PNLMS and NLMS by employing the sparseness measure into the PNLMS algorithm.	Analysed the existing developments in partial update and sparse adaptive filter algorithms.	SC-PNLMS     algorithm exhibits robustness to sparse and dispersive AIRs than PNLMS and NLMS for a modest increase in computational complexity.
12	Recent advances in partial update and sparse adaptive filters[36]	This paper discusses recently proposed techniques for sparse system identification, as well as the concept of joint partial and sparse updating for adaptive identification of sparse systems.		The paper illustrated the potential performance improvement that can be achieved by selective partial updates and sparse updates.

• XI.    Conclusions and prospects

In this paper we have presented the state of the art approaches for sparse adaptive filter methods for sparseness measure and echo cancellation for the last decade. From this survey, it is observed that the sparseness measure performance of the sparse adaptive filters have improved much compared to the using of conventional adaptive filters for network and acoustic echo cancellation and also we observed SC-PNLMS, SC-IPNLMS algorithms shown better performance than the conventional methods.