Существование апериодической траектории для внешних биллиардов вне правильных многоугольников

Для любой гладкой выпуклой кривой на. плоскости можно определить отображение внешности этой кривой в себя, называемое внешним биллиардом. А именно, обозначим кривую у, и пусть х — точка вне ее. Существуют две касательные к у прямые, проходящие через х; выберем одну из них, например правую относительно х, и, отразив х относительно точки касания, получим новую точку Тх.

Отображение Т называется внешним биллиардом; кривая у называется столом внешнего биллиарда.

Точку х вне фигуры назовем периодической, если существует такое натуральное п. что Т^пх = х, а периодом этой точки - минимальное такое п.

В случае, когда стол есть многоугольник, точки вне стола можно разбить на следующие три типа:

• 1)    точки с конечной траекторией (случай, когда Т^пх не определено для некоторого п);

• 2)    точки с периодической траекторией;

• 3)    точки с апериодической траекторией; в дальнейшем будем называть такие точки апериодическими.

В данной статье нас будут интересовать внешние биллиарды вне правильных многоугольников. Открытым в общем случае вопросом остается существование апериодической точки для внешнего биллиарда, вне правильных многоугольников. Внешние биллиарды вне правильных тре-, четырех- и шестиугольника, являются наиболее простыми случаями; несложно показать (см., например, [1-4]), что в этих случаях апериодической точки нет.

«Московский физико-технический институт (национальный исследовательский университет)», 2019

Табачникову в своей прорывной работе [1] удалосв показать, что существует апериодическая точка для внешнего биллиарда вне правильного пятиугольника; сделано это было с помощью впервые появившегося метода ренормализационной схемы.

Основным результатом настоящей статьи являются следующие теоремы, доказанные на основе ренормализационной схемы по Табачникову.

Теорема 1. Для внешних биллиардов вне правильных восьми- и двенадцатиугольника существуют апериодические точки.

Теорема 2. В случае внешних биллиардов вне правильных восьми- и двенадцатиугольника, периодические точки образуют вне столов мномсества полной меры.

Теорема 3 (случай восьмиугольника). В случае правильного восьмиугольника, все-возмомсные периоды периодических точек образуют мномсество

{- 4 * ( — 3) ^k + 12 * 9^k , 4 * 9^k , 4 * ( — 3) ^k + 12 * 9^k , 8Z + 8, — 4( — 3) ^k + (36 + 24Z) * 9^k , (8Z + 12) * 9 ^k , +4( - 3) ^k + (36 + 24Z) * 9 ^k | k,Z E Z> o}.

Теорема 3 (случай десятиугольника). Пусть В ₂ = { 7 (6^l+ 2 — ( — 1)) , 7(9 * 6 ^l+1 +2 * ( — 1) ^z ), 20 * 6^l, 30, 90 * 6^l, 10, 5, 20((78 + 120k) * 6^l — (k + 1) * ( — 1) ^z ), 7((276+240k) * 6 ^l — (2k+3) * ( — 1)), 7((234+180k) * 6 ^l +(2k+4) * ( — 1)), 7((34+40k) * 6 ^l +(2k+1) * ( — 1)), 10((20+40k) * 6 ^l +(2k+2) * ( — 1)), 40k+70, 7((306+180k) * 6 ^l +(2k+2) * ( — 1)), 40k+50, 60k+40, 30k+35, 20k + 30, 20k + 20,10k + 15, 10(6 ^l+ 2 — ( — 1)), 10((276 + 240k) * 6^l — (2k + 3) * ( — 1)), 10((34 + 40k) * 6 ^l + (2k + 1) * ( — 1) ¹ ), 60k + 70,20k + 30 | k,Z E Z> o}.

Тогда В ₂ есть множество всевозмозюных периодов периодических точек для внешнего биллиарда вне правильного десятиугольника.

Теорема 3 (случай двенадцатиугольника)

Введем следующие матрицы:

1	0	0	0	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0	0	0	0
Мб8 := 0	0	0	1	8	18	13	24	, М66 := 0	0	0	0	0	0
0	0	0	0	2	7	14	29	5	4	3	2	1	0
0	0	0	0	0	0	0	0	1	1	1	1	1	1

	2 2	2 2	2 2	2 2	20 20	50 50	26 26	50 50
	4	4	4	4	42	107	74	145
	2	2	2	2	20	50	48	94
М88 : =	0	1	0	0	0	0	0	0
	1	0	0	0	0	0	0	0
	0	0	0	1	8	18	13	24
	0	0	1	0	0	0	0	0

,

⎜0⎟

⎜1⎟

⎜2⎟

,

⎜0⎟

⎜1⎟

⎜1⎟

,

⎜0⎟

⎜2⎟

⎜1⎟

,

⎜0⎟

⎜1⎟

⎜3⎟

}■

Пусть

Н : =

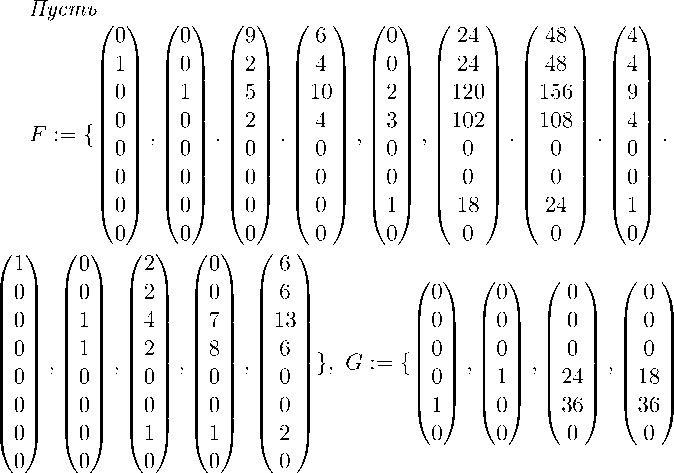
В := { 12

{М ^M^f | /

1 1 1 1 1)һ

€

ІІОЛ(12, (1 2 3 4 5 6) h)

Ғ,к,п € Z >o} U { М б₆ д | д € G,k € Z >o}, и пусть | һ € Н }. Множество всевозможных периодов

точек для внешнего биллиарда вне правильного двенадцатиугольника есть объединение В2 = В U { 2 * b\b € В, b пешшшор

Также в статье установлена в общем виде связь между внешними биллиардами вне правильных п- и ^-угольника, если п четно, а ^ нечетно. А именно, доказана

Теорема 4. Пусть п € Z >6; п чет но, а ^ нечетно. Пусть Т_п и Т л — внешние биллиарды вне правильных п- и 2-угольника, соответственно. Тогда:

• •    Апериодическая точка существует для Т_п, если и только если для Т л существует апериодическая точка;

• •    Периодические относительно Т_п точки образуют вне правильного п-уголъника-стола множество полной меры, если и только если периодические относительно Тл точки образуют вне правильного 2-угольника-стола множество полной меры.

Другими словами, проблемы периодичности для внешних биллиардов вне правильных п- 11 ^-угольника эквивалентны, если п нетію. а ^ нечетно.

Еще одним важным результатом оказывается

Теорема 5. Пусть п € Z >₄, п четно, у — правильный п-угольник, аТ_п - внешний биллиард вис у. Тогда сунщствуст ограиичсииая область Z С R 2\ y. т.ч. Т_п(Z ) С Z. и для Т_п выполнены следующие утверждения:

• •    Апериодическая точка р € R 2\ y существует, если и только если существует апе риодическая точка р € Z:

Автор выражает благодарность А. Я. Канелю-Белову за постаноку задачи и всестороннюю поддержку, а также А. Л. Семенова за плодотворные беседы и неоценимую помощь.

Работа была выполнена при поддержке гранта РИФ №17-11-01337.