Существует бесконечное количество пар простых чисел
Автор: Петров П.В.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Физико-математические науки
Статья в выпуске: 1-2 (76), 2023 года.
Бесплатный доступ
В статье рассматривается одна из старейших математических задач, существование пар простых чисел вида , , , у данной проблемы существует длительная история поиска решений. Один из таких результатов, является результат доказанный Бруном в 1919 г: «Ряд из величин, обратный простым близнецам, обрывается или сходиться», также таким результатом является достижение Джана Итена который в 2013 доказала что: «что существует бесконечно много пар последовательных простых чисел с разностью не более 70 миллионов». Далее данный результат был улучшен 2014 Пэйсом Нильсеном из унивирситета Брайгама Янга в Юте - 246. Моё решение не является продолжением работы Джана Итена, а является альтернативным способом решения, данной задачи. Данное решение будет изложено ниже и подразумевает под собой, решение данной задачи в более широком смысле, где проблема простых близнецов, является лишь частным случаем, более подробно об этом будет изложено в другой статье, а в данной же стать речь пойдёт именно о проблеме простых близнецов.
Построения последовательностей, симметричные остатки, полные комбинации остатков, эпициклоиды, нумерация комбинаций
Короткий адрес: https://sciup.org/170197655
IDR: 170197655 | DOI: 10.24412/2500-1000-2023-1-2-182-199
Текст научной статьи Существует бесконечное количество пар простых чисел
Таблица 1. n(N)- Количество простых чисел на промежутке [1: N].7г(N)-функция про- стых чисел.
|
1 |
2 |
3 |
4 |
,…, |
P- 1 |
P |
|
1/2 |
2/2 |
,…, |
||||
|
1/3 |
2/3 |
3/3 |
,…, |
|||
|
1/5 |
2/5 |
3/5 |
4/5 |
,…, |
||
|
,…, |
,…, |
,…, |
,…, |
,…, |
,…, |
,…, |
|
1/P |
2/P |
3/P |
4/P |
,…, |
(P — 1)/P |
P/P |
Согласно правилам:
-
1) Берётся один период каждой последовательности (1).
-
2) В данных периодах последовательностей, берётся каждый остаток каждой последовательности (1).
-
3) Для одной комбинации V берётся один остаток каждой последовательности (1).
-
4) Нумерация комбинаций начинается сверху вниз, согласно росту периодов последовательностей (1).
будет соответствовать, какое-либо целое число на промежутке [1: +^] .
Представим натуральный ряд в виде долей, согласно Теореме №1:
-
1) Если во множестве натуральных чисел 2,3,4,…,N зачеркнуть числа, кратным первым г простым числам 2,3,4,..., Рг , то первое (наименьшее) не зачёркнутое число будет простым.
-
2) Если вычеркнуть все чис л а, кратные всем простым числам до VN, т.е. выбрать г так, что Рг< VN < Рг+1 , то оставшиеся числа будут совпадать с множеством всех простых чисел Р , таких что 4N < Р < N .
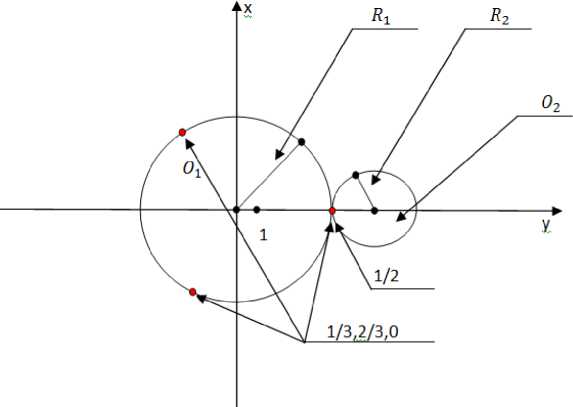
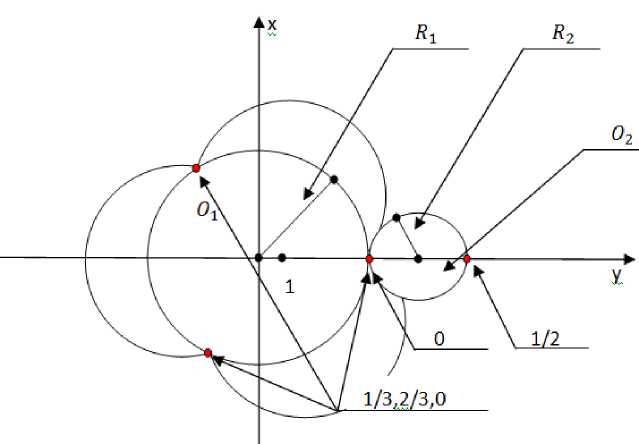
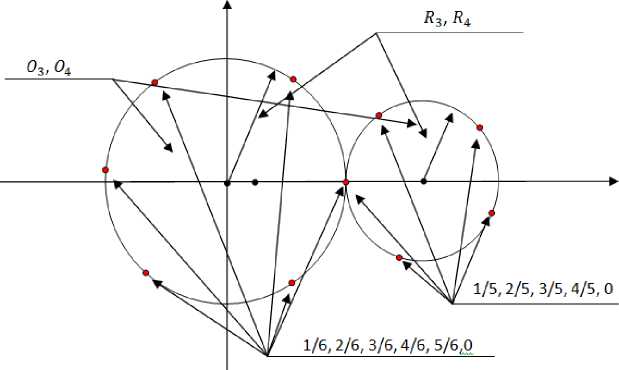
Разделим каждое число ряда {1,2,3,..., N2}, на числа 2,3,5,.,Р. P При этом будут браться, только простые числа из промежутка [1;М]. L = п(М) L — количество последовательностей. и(х) — функция простых чисел на промежутке [1; М] .Таблица №2 Таблица 2. Ряд ввиде долей представленный согласно Теореме №1 1 2 3 4 ,• •, М2 — 1 М2 1/2 2/2 3/2 4/2 ,• •, (М2 — 1)/2 М2/2 1/3 2/3 3/3 4/3 ,• •, (М2 — 1)/3 М2/3 1/5 2/5 3/5 4/5 ,• •, (М2 — 1)/5 М2/5 ,• • •, ,• • •, ,• • •, ,• • •, ,• •, ,-", ,-", 1/P 2/P 3/P 4/P ,• •, (М2 — 1)/P М2/Р Зададим данные последовательности с помощью формулы: S(n) = Gn n G [1,2,3, ...,М2] G = 1/T T G (1; М], T — простое число, G — коэффиценты последовательностей. Таким же образом будут получены последовательности (1): S(n) = 0,5n,S(n) = 0,33n,S(n) = 0,2n, ,„,S(n) = — n(1) nG [1,2,3,..., М2] Рассмотрим Таблицу 2: Таблица 2. Ряд ввиде долей, представленных согласно Теореме №1 1 2 3 4 ,-", М2 — 1 М2 1/2 2/2 3/2 4/2 ,-", (М2 — 1)/2 М2/2 1/3 2/3 3/3 4/3 ,-", (М2 — 1)/3 М2/3 1/5 2/5 3/5 4/5 ,-", (М2 — 1)/5 М2/5 ,• ^, ,• ^, ,• ^, ,• ^, ,-", ,-", ,-", 1/P 2/P 3/P 4/P ,-", (М2 — 1)/P М2/P Данная Таблица №2 получена путём подстановки в последовательности (1), целых чисел n, n G [1,2,3, ...,М2]. Данную подстановку назовём естественным ходом, заполнение Таблицы №2. Данную Таблицу №2, можно разделить на комбинации остатков. Одной комбинацией остатков называется значение последовательно- стей (1) при n = d, где d- некоторое целое число, принадлежащее промежутку [1;М2]. Общее количество комбинаций будет определяться числом М2, так как данное число является наибольшем в промежутке [1; М2]. S(n) = 0,2n,-,S(n) = (~)n, S(n) = (~)n, n = d S(d) = 0,2d,-,S(d) = 0-) d, S(d) = (1) d, n = d 0,2d = Ц1 + t1 (^1)d = ap1 + tp1 (pz)d ap2+tp2 (t1,..., tp , tp) — комбинация остатков при числе d. dG[1;N2]. Количество остатков будет соответствовать количеству простых чисел на промежутке [1; N] то есть функции n(N) х = N. Отсюда получим правило получения комбинаций: «Для любого целого числа d, d G [1; N2] берётся один остаток в каждой последовательности (1)». Теперь рассмотрим другой способ получения комбинаций: Так как последовательности (1) имеют периоды, 2,3, .,Р. То количество различных остатков, каждой последовательности, будет определяться одним периодом каждой последовательности (1), отсюда правило: Для составления комбинаций берётся один период каждой последовательности (1). Это следует из Теоремы №1 так как на основе данной теоремы получены последовательности (1). Составим Таблицу 3: Таблица 3 Значения остатков последовательностей (1), равные одному периоду каждой последовательности (1), периоды простые числа 1 2 3 4 ,• •, P — 1 P 1/2 2/2 ,• • •, 1/3 2/3 3/3 ,• • •, 1/5 2/5 3/5 4/5 ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• •, ,• •, 1/Р 2/Р 3/Р 4/Р ,• •, (P — 1)/P P/P Данные комбинации могут получаться методом перебора, согласно правилу, полученному из выше сформулированного правила (из естественного хода заполнения Таблицы №2): «Для любого числа d, d G [1; N2] берётся один остаток в каждой последовательности». Из данного правила получим формулировку: «Для любой одной комбинации «V» берётся один остаток в одном периоде каждой последовательности (2)». Теперь рассмотрим получения комбинаций естественным ходом, количество их условно ограниченно промежутком [1; N2], но при необходимости подстановку значений в последовательности (1), можно продолжать не ограниченно. n G [1,2,3, ., N2, N2 + 1, N2 + 2, .,+ю]. Теперь необходимо доказать, что при получении комбинаций естественным ходом, при неограниченном заполнении, используются все остатки 1-го периода, каждой последовательности (1): Доказательство: Рассмотрим Таблицу №3: Таблица 3. Значения остатков последовательностей (1), равные одному периоду каждой последовательности (1), периоды простые числа 1 2 3 4 ,• •, P — 1 P 1/2 2/2 ,• • •, 1/3 2/3 3/3 ,• • •, 1/5 2/5 3/5 4/5 ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• •, ,• •, 1/P 2/P 3/P 4/P ,• •, (P — 1)/P P/P Так как данные последовательности(1) имеют периоды то они периодические, то рассмотрим две 1-ые последовательности: S(n) = 0,5n, S(n) = 0,33(3)n, и их периоды Т1 = 2, Т2 = 3, представим естественный ход заполнения при не ограниченном росте n G [1,2,3, .,N2,N2 + 1,N2 + 2, ., +^], в виде движения двух окружностей, O1 — не подвижная, 02 — подвижная, то есть если R1 = 3, R2 = 2. Эпициклоида – плоская кривая, образуемая фиксирован- ной точкой окружности, катящейся по скольжения. Рисунок 1. внешней стороне другой окружности без Рис. 1 01 — не подвижная окружность (направляющая), 02 — подвижная окружность (производящая), R1 — радиус не подвижной окружности, R2 — радиус подвижной окружности Мы имеем право так представлять, так как последовательности S (п) = 0,5п, S (п) = 0,33(3)п-периодические. То по свойствам эпициклоид имеем: Количество точек невозврата на неподвижной окружности 01, от подвижной окружности 02, будет определяться радиусом не подвижной окружности R1 (I = 3), i —количество точек невозврата. Это следует из того, что R1 не кратно R2, а это следует из определения простого числа: «Натуральное число Р называется простым, если Р > 1 и Р не имеет положительных делителей, отличных от 1 и Р». То есть если периоды последовательностей(1) простые числа, то радиусы их не могут быть кратны друг другу. А это значит, что остаток 1/2, последовательности S(n) = 0,5п, п G [1,2, „.,+го], будет иметь три различные точки на окружности 01. То есть комбинации остатков: {1;|}, {|;|}, {1; о}. С последовательностью S(n) = 0,33(3)п, п G [1,2, ™,+ю]. Рисунок №2 Если на окружности 02 взять точку 0, (остаток 0), то есть совершить поворот окружности 02 на 180-градусов, остаток 0 будет иметь три различные точки на окружности 01. То есть комбинации остатков: {о; |}, {о; |}, {0; 0}. Это следует из того, что при повороте окружности 02, отношения радиусов окружностей не меняется. Рисунок 3. Рис. 2. Точки невозврата, полученные путём построения эпициклоиды, полученные с помощью двух окружностей 01, 02. Рис. 3 Точки невозврата, полученные путём построения эпициклоиды, с помощью двух окружностей 01, 02. Окружность 02 совершила поворот на 180 градусов. Если построить эпициклоиду, при этом использовать обе точки 0 и 1/2, то получиться 6 точек, на окружности 01, то есть определить общее количество комбина-ций:{2:9- О Ы- Й- К}{0:0} Теперь к двум первым последовательностям S(n) = 0,5n, S(n) = 0,33(3)n n е [1,2, „.,+го], прибавим третью последовательность S(n) = 0,2n n е [1,2, .„,+ю]. Общий период первых двух последовательностей, будет определяться как Т1-2 = 6, то возьмём радиус окружности 03, R3 = 6, а радиус окружности 04, R3 = 5, То по свойствам эпициклоид имеем: Количество точек не возврата на неподвижной окружности 03, от подвижной окружности 04, будет определяться радиусом не подвижной окружности R3(i = 6), i —количество точек не возврата. Это следует из того, что R1 не кратно R2, а это следует из определения простого числа: «Натуральное число Р называется простым, если Р > 1 и Р не имеет положительных делителей, отличных от 1 и Р». То есть число 6 взаимно-простое с числом 5, так как множители 2 и 3 не кратны 5. Рисунок 4. Рис. 4. Точки невозврата, полученные путём построения эпициклоиды, с помощью двух окружностей 03, 04. А это значит, что остаток 1/5 последовательности S(n) = 0,2n, n e [1,2, .„, +^], будет иметь 6 различных точек на окружности 03. То есть комбинации остатков: {i;i}-(1;S-{1=3}-{1=4}-{1;|}-{1;0), с b ОУ kb ОУ kb ОУ kb ОУ kb ОУ kb последовательностью S(n) = 0,166(6)n, n€[1,2,^,+ro]. Или остаток 1/5, будет иметь комбинации остатков с комбинациями остатков, полученных от последовательностей S(n) = 0,5n, S(n) = 0,33(3)n n e [1,2, ^,+^], {1;1;1}, {1;2;1}, {1; 0;1}, {0;1; 1}, {o;2;1}, {0; 0; 1} 12 3 bJ 12 3 bJ (2 bl I 3 bJ I 3 bJ ( bJ . Так как количество различных комбинаций первых двух последовательностей будет определяться как общий знаменатель периодов двух последовательностей: 2x3 = 6. Если на окружности O3 взять точки |, |, 4 -, 0, и совершать повороты окружности О3, на определённый градус соответствующим точкам, то каждой такой точке будет соответствовать, комбинации остатков: 112 122 1 2 12 222 {2;3 ;5Г {2; 3 ;5Г{2 ;0;5),{0;3; 5У {0;3;5Г {0; 0 5} 113 123 1 3 13 233 {2;3;5},{2;3;5},{2;0;5},{0;3;5},{0;3;5],10;0;5] (1 1 4) (1 2 4) (1 4) ( 1 4) ( 2 4) Г4) {2; 3; 5}, {2; 3; 5}, {2; 0; 5}, {0; 3; 5}, {0; 3; 5}, {0; 0; 5} {2:1:0}-{|;1:0}'{|;0:0}'{0;|;0}'{0;|;0}-{0;0:0} Это следует из того, что при повороте окружности О3, отношения радиусов не меняется. При этом количество, различных комбинаций можно посчитать, как общий знаменатель трёх последовательностей: 2 X 3 X 5 = 30. Соответственно, добавляя по очереди, следующие последовательности к последовательностям: S(n) = 0,5n, S(n) = 0,33(3)n, S(n) = 0,2n, n e [1,2, ^,+^], периоды, которых простые числа, лежа- щие на промежутке [1;^]: S(n) = 0,142n, S(n) = 0,09(09)n,_, S(n) = - x n, S(n) = " ' Pi P2Xn’ e [1,2.....+^j, будем получать, комбинации остатков, при этом каждая комбинация уже полученных комбинации остатков, будет иметь комбинации, со всеми остатками, следующей последова- тельности, это следует из того что, все периоды последовательностей простые числа, а это значит, что общий период уже полученных комбинаций остатков, будет состоять из простых чисел, то есть 2x3x5 = 30, взаимно-простое с 7, соответственно 30x7 = 210 взаимно-простое с 11, 210x11 взаимно-простое с 13,..., 210 X 11 X 13, .„,Р1, взаимно-простое с Р2. «Натуральное число Р называется простым, если Р > 1 и Р не имеет положительных делителей, отличных от 1 и Р», то есть: период 2 не имеет общих множителей с периодами {3,5,7,^,Р1,Р2}, кроме 1-цы также 3 не имеет общих множителей с периодами {2,5,7,^,Р1, Р2}, кроме 1-цы, также 5 не имеет общих множителей с периодами {2,3,7,^,Р1, Р2}, кроме 1-цы, также 7 не имеет общих множителей с периодами {2,3,5,^,Р1, Р2}, кроме 1-цы, также Р1 не имеет общих множителей с периодами {2,3,5,..., Р2}, кроме 1-цы, также Р2 не имеет общих множителей с периодами {2,3,5,^, Р1} кроме 1-цы, {2,3,5,7,^,Р1, Р2} e[1;^j, 2 < 3 < 5 < 7 <, .„,< Р1 < Р2 А это значит, что при получении комбинаций естественным ходом, при неограниченном заполнении, используются все остатки 1-го периода, каждой последовательности (1). Отсюда правило для получения комбинаций методом перебора: «В данных периодах последовательностей, берётся каждый остаток каждой последовательности (1) на одном периоде.» (3) Что и требовалось доказать. Выпишем все правила, и добавим 4-ое: 1) Для составления комбинаций берётся один период каждой последовательности. 2) «Для любой комбинации «V» берётся один остаток в одном периоде каждой последовательности. 3) В данных периодах последовательностей, берётся каждый остаток каж- 4) Нумерация комбинаций начинается сверху вниз, согласно росту периодов последовательностей (1). Это следует из Теоремы №1, так как согласно работы данной Теоремы в промежуток [1; N], как добавляются простые числа. Таблица-дополнение. Одна комбинация выделенная красным маркером, полученная методом перебора, согласно выше описанным правилам, количество остатков, равно ко- Составим Таблицу №4, методом перебора согласно выше описанным правилам: Таблица 4. Комбинации остатков, полученные методом перебора, из Таблицы-дополнение, по выше изложенным правилам. При этом верхняя строчка является номером комбинации, а не числом п, п Е [1; +от] 1 2 3 4 , ”, F-2 F- 1 F Я11 Я21 Я31 Я41 , ”, Ян-21 Ян-11 Ян1 <712 Я22 Я32 Я42 , ”, Ян-22 Ян-12 Ян2 <713 Я23 Я33 Я43 , ”, Ян-23 Ян-13 Ян3 , ■ ”, , ”, , ”, , ”, , ”, , ”, , ”, , ”, Я1Р Я2Р Я3Р Я4Р , ”, Ян-2Р Ян-1Р ЯнР Так как комбинации остатков, полученные методом перебора из Таблицы – дополнение, содержащиеся в Таблице №4 получены согласно правилам, при этом данные правила вытекают из выше доказанного, то есть из заполнения Таблицы №3 естественным ходом, при неограниченном росте п Е [1; +^], а это правила: 1) Для составления комбинаций берётся один период каждой последовательности. 2) «Для любой комбинации «V» берётся один остаток в одном периоде каждой последовательности. 3) В данных периодах последовательностей, берётся каждый остаток каждой последовательности (1) на одном периоде. 4) Нумерация комбинаций начинается сверху вниз, согласно росту периодов последовательностей (1). То каждая комбинация, полученная методом перебора, будет соответствовать, какому-либо целому числу на промежутке [1; +^], но при этом при составлении комбинаций методом перебора нельзя сказать какому именно целому числу (п) на промежутке [1; +^], будет принадлежать, какая-либо комбинация остатков. Комбинации остатков, полученные методом перебора из Таблицы – дополнение, разделим на полные и не полные комбинации. Полные комбинации остатков – это комбинации, полученные методом перебора, и соответствующие какому-либо целому числу на промежутке [TV; TV2], то есть количество остатков у данной комбинации будет равно, количеству последовательностей (1), то есть количеству простых чисел на промежутке [1; W]. h(N). Не полные комбинации остатков - это комбинации, полученные методом перебора, не соответствующие какому-либо числу на промежутке [1; TV2], то есть количество остатков у данной комбинации будет не равно, количеству последовательно- стей (1), то есть количеству простых чисел на промежутке [1; V]. h(N) Для того чтобы данную комбинацию сделать полной, необходимо увеличить промежуток [1; N + О]. h(N + О), то есть увеличить количество простых чисел, соответственно и последовательностей (1). Что и требовалось доказать. Теорема №4. Существует бесконечное количество пар простых чисел Р1 и Р2, где Р2 — Р1 = 2. Таблица 1. один период каждой последовательности (1) 1 2 3 4 5 ,• •, Р 2 1/2 2/2 ,• •, 3 1/3 2/3 3/3 ,• •, 5 1/5 2/5 3/5 4/5 5/5 ,• •, ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• •, ,• •, Р 1/Р 2/Р 3/Р 4/Р 5/Р ,…, Р/Р Рассмотрим, Таблицу №1 выделив остатки 1-го и 3-его столбца, соответствующие числам 1 и 3. 1 и 3 столбцы содержат остатки: 1111 (2'3'5' (1 3 {2'°'5' -й Докажем, что существует бесконечное количество чётных чисел имеющие не симметричные остатки с остатками чисел 1 и 3 то есть такие чётные числа что в сумме с остатками чисел 1 и 3 дают остатки удовлетворяющие условию (1): Числа 1, 3, чётное число F: ij1'1'!' ^'Ц и 3{~■|■|■ ^'Ц, F{ai'а2, аз, а4, ».,aw}- остатки чисел 1,3, F. V2 3 5 Р J V2 3 5 Р V 1 + F = С, С —некоторое простое число. — + а, = с + (1 - + а2 = с + (2 — + а4 = с + (4 ' " •' — + ар = с + (р При этом остатки числа С будут удовлетворять условию: ° < (1 <1 ° < (2 <1 ° < (4 <1 0 < tp < 1 3 + F — D, D -некоторое простое число. — + «i — d + k 2 1 1 - + «2— d + k2 — + «4 — d + k4 , ., ~ + Up — d + kp При этом остатки числа D будут удовлетворять условию: 0 < k1 < 1 0 < k2 < 1 0 < k4 < 1 ,, 0 < kp < 1 Данные условия получены с помощью Теоремы №2: Любое составное число С С G [N;N2] можно представить в виде суммы двух целых чисел С — А + В, при этом А и В, будут иметь симметричные остатки. Любое простое число D D G [N;N2] можно представить в виде суммы двух целых чисел D — F + К, при этом F и К, будут иметь не симметричные остатки. Остатки целого числа А принадлежащего промежутку [1;N2], есть остатки полученные путём деления числа А на числа из промежутка [1; N], А («1, и2, «3,..., aw}. Остатки целого числа В принадлежащего промежутку [1;N2], есть остатки полученные путём деления числа В на числа из промежутка [1; N], В (Ь1, b2, b3,..., bN}. Остатки чисел А и В, являются не симметричными друг относительно друга, если целое число D, полученное с помощью суммы чисел А + В — D, где D имеет остатки удовлетворяющие условию: D(0 < d1 < 1,0 < d2< 1,0 < d3< 1,.,0 Остатки чисел А и В, являются симметричными друг относительно друга, если целое число D, полученное с помощью суммы чисел А + В — D, где D имеет остатки удовлетворяющие условию: D(0 < d1 < 1,0 < d2< 1,d3 — 0, .„, 0 < dN< 1}, D принадлежит промежутку [1; N2], то есть остатки целого числа D (так как А и В - целые то D - целое) могут быть также получены путём деления целого числа D на числа из промежутка [1;N]. То есть D — будет составным числом, так как делиться на цело на какое-либо из промежутка [1; N]. Доказательство: Рассмотрим Таблицу 1. Таблица 1. 1 2 3 4 5 ,…, Р 2 1/2 2/2 ,…, 3 1/3 2/3 3/3 ,…, 5 1/5 2/5 3/5 4/5 5/5 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/р 2/Р 3/Р 4/Р 5/Р ,…, Р/Р Так как из Теоремы №3 следует, что любая комбинация остатков, полученная по правилам: 1) Берётся один период каждой последовательности (1). 2) В данных периодах последовательностей, берётся каждый остаток каждой последовательности (1) 3) Для каждой комбинации V берётся один остаток одного периода каждой последовательности (1) 4) Нумерация комбинаций начинается сверху вниз, согласно росту периодов последовательностей (1) Будет соответствовать, какому-либо целому числу, которых бесконечное количество, то уберём в каждой последователь- ности (1) Таблицы №1 остатки симметричные остаткам чисел 1 и 3. Рассмотрим последовательности (1), в Таблице №1, все данные последовательности формируются по одному ниже изложенному принципу: Разделим каждое число ряда {1,2,3, .,N2}, на числа 2,3,5,., Р. P L = tt(N) L — количество последовательностей. •п(х) — функция простых чисел на промежутке [1; N]. Таблица 2. 1 2 3 4 ,• • •, N2 — 1 N2 1/2 2/2 3/2 4/2 ,• • •, (N2 — 1)/2 N2/2 1/3 2/3 3/3 4/3 ,• • •, (N2 — 1)/3 N2/3 1/5 2/5 3/5 4/5 ,• • •, (N2 — 1)/5 N2/5 ,• • •, ,• • •, ,• • •, ,• • •, ,• • •, ,• ^, ,• ^, 1/Р 2/Р 3/Р 4/Р ,• •, (N2 — 1)/Р N2/P Зададим данные последовательности с помощью формулы: S(n) = Gn n E (1,2,3, ., N2] G = 1/Т Т E (1; N], Т — простое число, G — коэффиценты последовательностей. Таким же образом будут получены последовательности: S(n) = 0,5n,S(n) = 0,33n,S(n) = 0,2n, .„,S(n) = — n(1) ne[1,2,3,m,N2] Рассмотрим последовательность №1 Таблица №2: S(n) = 0,5n, n E [1,2,3, ., N2], данная последовательность имеет период 2, а это будет означать, что количество различных значений остатков, в последовательности S(n) = 0,5n будет рано 2-ум {1; о}. Теперь рассмотрим остатки чисел 1 и 3 в последовательности S(n) = 0,5n, n E [1,2, ^,N2] (Также и при не ограниченном росте n, n E [1,2,...,+^]) , числам 1 и 3 будет соответствовать остаток 1/2, так как 0,5n = 0,5 х 1 = 0,5, 0,5n = 0,5 х 3 = 1,5 = 1 + 0,5. Остаток «0» будет не симметричен остаткам чисел 1 и 3, так как 1 + 0=1 , 0 < 1 < 0 — по Теореме №2 (оста-ток1/2 не симметричен остатку 0), данный остаток удовлетворяет условию (1): 0 < ^ < 1 0 < ^ < 1 Так как остаток «0», в последовательности S (п) = 0,5п, будет соответствовать числу п = 2, и при этом период данной последовательности S(n) = 0,5п Г = 2, то зададим формулой (1), все значения на промежутке пЕ [1,2, .,N2](Также и при не ограниченном росте п, п Е [1,2, .,+^]) при которых последовательность S (п) = 0,5п, будет иметь остаток «0»: /(к) = 2 + 2к(1) Где к Е [0,1,2, ... N21 у]’ При этом N-, при не чётном N , будет округляться в большую сторону. (Также и при не ограниченном росте п, п Е [1,2,..., +“]), 2— значение последовательности S(n) = 0,5п, при п = 2, коэффициент «2», в выражении 2k, есть период последовательности S(n) = 0,5п При этом все значения формулы №1, будут принадлежать значениям промежутка п Е [1,2, .,N2], так как в данный промежуток входят, чётные и не чётные числа, так как разница между любыми соседними числами будет равна 1-цы, △= 2 — 1 = 1, задано условиями последовательности S(п) = 0,5п. п Е [1,2, .,N2](Также и при не ограниченном росте п, п Е [1,2,.,+^]) Так как в формуле (1), всегда можно вынести двойку за скобку, то это будет значить, что при любом к Е [0,1,2, .,“], (Также и при не ограниченном росте п, п Е [1,2, ..., +^]), число /(к) — чётное. /(к) = 2 + 2к(1) /(к) = 2 + 2к = 2 х (1 + к)(1) А это значит, что все возможные комбинации остатков, удовлетворяющие условию (1) в последовательности S(п) = 0,5п, будут чётными числами. Теперь рассмотрим последовательно-сти(1), так как данные последовательности имеют периоды Г Е (1; N], Г — простое число, то данные последовательности пе- риодические, то все возможные остатки каждой последовательности(1), при любом п Е [1,2, ., N2], (Также и при не ограниченном росте п, п Е [1,2, ..., +“]), будут определены на одном периоде каждой последовательности (1), составим Таблицу №3: Таблица 3,1-н период каждой последовательности (1) 1 2 3 4 5 ,…, Р 2 1/2 2/2 ,…, 3 1/3 2/3 3/3 ,…, 5 1/5 2/5 3/5 4/5 5/5 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/Р 2/Р 3/Р 4/Р 5/Р ,…, Р/Р Выпишем одного периода каждой по- следовательности (1) получим следующие: гласно одному периоду последовательности. {2-2} — значения последовательности S(п) = 0,5п , п Е п Е {1,2}, согласно од- ному периоду последовательности. {Н’3} — значения последовательности S(п) = 0,33(3)п при п Е {1,2,3}, согласно одному периоду последовательности. { '1 2 3 4 5 5 ’ 5 ’ 5 ’ 5 ’ 5. }— значения последователь- ности S(п) = 0,2п при п Е {1,2,3,4,5} со- (1 2 3 4 5 Iр’р’р’р’р вательности 3- значения последо- S (п) = 1 х п п Е {1,2,3,4,5, ., Р} согласно одному периоду последовательности. Строчки каждой последовательности(1), длиной в один период. Так как данные строчки получены, по одному и тому же принципу, вытекающего из построения последовательностей (1). (То есть из Теоремы №1 См. ниже). То не будим рассматривать каждую строчку, а рассмотрим некую общую строчку, назо- вём данную строчку P". Pi -есть некое простое число, Pi е [1; V]. Рассмотрим, некое простое число Pi данное число принадлежит некоему промежутку [1; V], Pi< V . 1 2 3 4 5 PpPpPpPpPp Р"} Pi} Тогда количество различных элементов в строчке P", будет определяться согласно периоду последовательности Т = P", S(n) = рп. п е {1,2,3, .„,P"}. Обозначим элементы множества {г,р,р,^,]7, -„’P1}, буквой U. Так как мы берём только остатки, то остатком ■ ,о} е последнего элемента во множестве U , будет 0. Так как р + 0 = р. (]1,р,р,р,р, U. Теперь необходимо доказать, что если из Pi вычесть любой элемент из множества U, то мы получим элементы из множества U. То есть: Pi —0 Pi =-- Pi Pi Pi 1 _ Pi-1 — Pi Pi Pi Pi _ Pir- -— Pi Pi Pi Pi 3 _ Pi-3 — Pi Pi Pi Pi Pi-- -— Pi Pi Pi Pi 5 Pi-5 — Pi Pi Pi Pi Pi-1 _ 1 Pi "р?" - Pi будет принадлежать множеству U —будет принадлежать множеству U — будет принадлежать множеству — будет принадлежать множеству — будет принадлежать множеству — будет принадлежать множеству — будет принадлежать множеству U При этом каждое выражение, можно представить виде произведения: р11 — = — х (P") где (P") е {1,2,3, .’P"}, так как разница между любыми соседними эле ментами будет 1-ца, △= 1, это следует из условий, с помощью которых были заданы последовательности (1). — = р х (Pi — 1) где (Pi — 1) е {1,2,3P -ir- = - х (Pi — 2) где (Pi — 2) е {1,2,3P Pi -ir- = г х (Pi — 3) где (Pi — 3) е {1’2,3P -i "ir5 = - х (Pi — 4) где (V — 4) е {1,2,3P -i ,…, 1 -х(Pi —(Pi —1)) где 1е {1,2,3P -i То есть элементы {P", (P" — 1), (P" — 2), (P" — 3), (P" — 4), (P" — 5), .„,1} будут соответствовать множеству {1,2,3, „,P"}, то есть P" = P", (P" — 1) = (P" — 1), (P" — 2) = (P" — 2), (Pi — 3) = (P" — 3), (P" — 4) = (P" — 4), (P" — 5) = (P" — 5),_,1=1. А это будет означать, что подставив значения {(P" — 1), (P" — 2), (P" — 3), (P" — 4), (P" — 5), .„,1} мы получим 1 значения последовательностей S(n)= — п при {1,2,3, .,P"} или {P", (P" — 1), (P" — 2), (Pi — 3), (Pi — 4), (Pi — 5), .„,1), то есть множество значений U. А это значит, что если из у вычисть любой элемент из множества U,to мы получим элементы из множества U. Рассмотрим выражения: Pi — ' - 0 = -,, где eU Pi P Pi Pi 1 Pi-1 P-1 „ — = n ,где Ar- e U Pi Pi Pi Pi Pi 2 Pi-2 P-2 „ — = n ,где Ar~ e U Pi Pi Pi Pi Pi 3 Pi-3 P-3 „ — = —-—, где Ar- e U Pi Pi Pi Pi Pi 4 Pi -4 P - 4 — = n ,где Ar- e U Pi Pi Pi Pi Pi 5 Pi-5 P-5 — = —-—, где Ar- e U Pi Pi Pi Pi , Pi P, - 1 1 1 — ----= —, где — e U Pi Pi Pi Pi Каждое данное выражения, можно представить в виде уравнения: %4 Pi р;-х = у • 1 2 3 4 5 Р^СР^СР^^^,- Pi-1 Pi ,о} Так как данное уравнение представляет собой уравнение 1-ой степени, то это будет означать, что данное уравнение имеет один корень, а это значит, что одному из возможных значений %, будет соответствовать только одно значение у. А это будет означать, что любому остатку из множества U, будет соответствовать один симметричный остаток, из множества U. Pi - Pi Pi Pi - Pi Pi Так как изначально рассматриваются, два не чётных числа 1 и 3 то в строчке Pi им будут соответствовать остатки: 1/Pi и 3/Pi. То определим количество не симметричных остатков обоим остаткам в строчке Pi или во множестве U. Так как каждому остатку во множестве U, будет всегда соответствовать один симметричный остаток, из множества U, то найдём для остатков 1/Pi и 3/Pi симметричные остатки: Pi-1 Pi Pi-3 Pi А это будет означать, для двух остатков, количество не симметричных остатков во множестве U, будет определяться по формуле: ^ = Pi-2 Где ц- количество не симметричных остатков остаткам 1/Pz и 3/Pz, Pz - количество остатков во множестве U, 2-это симметричные остатки, остаткам 1/Pz и 3/Pz во множестве U. Теперь рассмотрим строчку 1 в Таблице №1: 1/2 2/2 Так как у последовательности S(n) = 0,5п, соответствующих 1-ой строчке будет период 2, то количество различных остатков будет равно двум: 1/2 0. То в числах 1 и 3 данные последовательности имеют значения 1/2, а это значит, что числу 1 и 3 будет соответствовать один не симметричный остаток 0, соответствующий чётному числу: Z = P-1(1) Где ц- количество не симметричных остатков остаткам 1/2. P- количество остатков во множестве U, 1- не симметричный остаток остатку 1/2. Z = P Где P — количество остатков в строчке, 2- количество симметричных остатков остаткам чисел 1 и 3, в любой строчке. Это следует из того, что все строчки получены, по одному и тому же принципу, вытекаю- Для всех остальных строчек в Таблице №1, количество не симметричных остатков для остатков чисел 1 и 3 будет определяться по формуле(2), так как числа 1 и 3 будут иметь различные остатки, в одном периоде каждой последовательности(1): 2(2) щего из построения последовательностей (1). (То есть из Теоремы №1) Составим Таблицу №4, из Таблицы №1 исключив все симметричные остатки остаткам чисел 1 и 3: Таблица 1. 1 2 3 4 5 ,…, P 2 1/2 2/2 ,…, 3 1/3 2/3 3/3 ,…, 5 1/5 2/5 3/5 4/5 5/5 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, P 1/P 2/P 3/P 4/P 5/P ,…, P/P Таблица 4. Не симметричные остатки, остаткам чисел 1 и 3. 1 2 3 4 5 ,…, P 2 2/2 ,…, 3 1/3 ,…, 5 1/5 3/5 5/5 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, P 1/P 2/P 3/P 4/P 5/P ,…, P/P Таблица 4. Не симметричные остатки, остаткам чисел 1 и 3. 1 2 3 4 5 ,…, Р 2 2/2 ,…, 3 1/3 ,…, 5 1/5 3/5 5/5 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/Р 2/Р 3/Р 4/Р 5/Р ,…, Р/Р 2 х 3 х 5 х 7 х,_,хР = Q(2) Тогда получим некое целое чётное чис- жение №1 всегда можно вынести 2-ку за ло Q (Q — будет всегда четным, сколько скобку): множителей мы не взяли, так как в выра- 2 х (3 х 5 х 7 х, ,„,х Р) Теперь представим данное число в виде тельных последовательностей, для лучшей Таблицы№5 последовательностей (1) (до- визуализации): бавим в Таблицу №5 несколько дополни- Таблица 5. Число Q-представленное в виде Таблицы. Q 2 1/2 0 3 1/3 2/3 0 5 1/5 2/5 3/5 4/5 0 7 1/7 2/7 3/7 4/7 5/7 6/7 0 11 1/11 2/11 3/11 4/11 5/11 6/11 7/11 8/11 9/11 10/11 0 13 1/13 2/13 3/13 4/13 5/13 6/13 7/13 8/13 9/13 10/13 11/13 12/13 0 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/Р 2/Р 3/Р 4/Р 5/Р 6/Р ,…, (Р -6)/Р (Р — 5)/Р (Р — 4)/Р (Р -3)/Р (Р -2)/Р (Р — 1)/Р 0 Таблица 6. Число Q-представленное в виде Таблицы, с добавленными периодами, для лучшей визуализации Q 2 1/2 0 1/2 0 3 1/3 2/3 0 5 1/5 2/5 3/5 4/5 0 7 1/7 2/7 3/7 4/7 5/7 6/7 0 11 1/11 2/11 3/11 4/11 5/11 6/11 7/11 8/11 9/11 10/11 0 13 1/13 2/13 3/13 4/13 5/13 6/13 7/13 8/13 9/13 10/13 11/13 12/13 0 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/Р 2/Р 3/Р 4/Р 5/Р 6/Р ,…, (Р - 6) /Р (Р -5) /Р (Р — 4) /Р (Р — 3) /Р (Р — 2) /Р (Р — 1) /Р 0 Теперь в Таблице №6, уберём симметричные остатки остаткам чисел 1 и 3 Таблица №7: Таблица 7. Число, Q-представленное в виде Таблицы, в котором в каждой последова- тельности (1), вычеркнули симметричные остатки, остаткам чисел 1 и 3 Q 2 — 0 — 0 3 1/3 — — 5 1/5 — 3/5 — 0 7 1/7 2/7 3/7 — 5/7 — 0 11 1/11 2/11 3/11 4/11 5/11 6/11 7/11 — 9/11 — 0 13 1/13 2/13 3/13 4/13 5/13 6/13 7/13 8/13 9/13 — 11/13 — 0 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/Р 2/Р 3/Р 4/Р 5/Р 6/Р ,…, (Р —6) /Р (Р — 5) /Р (Р — 4) /Р — (Р — 2) /Р — 0 Теперь вычтем из целого чётного числа Q, число 2 и получим чётное число Q — 2. Данное число будет также чётным, так как Q -чётное. Таблица 8. Число, Q-2-представленное в виде Таблицы Q-2 Q 2 — 0 0 3 1/3 — — 5 1/5 — 3/5 0 7 1/7 2/7 3/7 — 5/7 0 11 1/11 2/11 3/11 4/11 5/11 6/11 7/11 — 9/11 — 0 13 1/13 2/13 3/13 4/13 5/13 6/13 7/13 8/13 9/13 — 11/13 — 0 ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, ,…, Р 1/Р 2/Р 3/Р 4/Р 5/Р 6/Р ,…, (Р — 6)/Р (Р — 5)/Р (Р — ^)/Р — (Р — 2)/Р — 0 Количество не симметричных остатков в 1-ой строчке будет рассчитываться по формуле №2: ц = P — 1(1) —для первой строчке Где ц — количество не симметричных остатков, P — количество остатков в строчке. 1- не симметричный остаток остатку 1/2. Количество не симметричных остатков для остальных строчек будет рассчитываться по формуле №3: ц = P — 2(2) —для остальных строчек Где / — количество не симметричных остатков, Р — количество остатков в строчке. 2- количество симметричных остатков остаткам чисел 1 и 3, в любой строчке. Теперь необходимо доказать, что из Таблицы №4, можно получить бесконеч- ное количество комбинаций, имеющих не симметричные остатки, с соответствующими остатками чисел 1 и 3. И каждой такой комбинации соответствует какое-либо чётное число. Доказательство: Рассмотрим Таблицу №4: Так как множество комбинаций остатков полученных из Таблицы №1, будет включать в себя, всё множество комбинаций полученных из Таблицы №4, так как соответствующая строчка Таблицы №1 включает в себя все остатки соответствующей строчки Таблицы №4, то из Теоремы №3, будет следовать, что каждой такой комбинации остатков, полученных по правилам Теоремы №3, из Таблице №4, будет соответствовать некое целое число на промежутке [1; +^). Из доказанного выше также следует, что каждое такое целое число, будет чётным. Тогда возьмём и перемножим последовательности в таблице №4, соответственно выражение (1) может состоять из сколько угодно множителей: Данное расположение последовательностей (1) в числе Q будет обусловлено тем, что данное число делиться на любой множитель из множителей: 2,3,5,7,..., Р. Теперь добавим к первой последовательности (1), дополнительные периоды. (для лучшей визуализации) получим Таблицу №6: Число Q — 2 есть число F удовлетворяющие условию(1), так как все симметричные остатки остаткам чисел 1и 3 в после-довательностях(1), будут отстоять от значения 0-то есть нулевого остатка в после-довательностях(1), на 1-цу и 3-ку. Число Q — 2 удовлетворяющие условию (1), существует пока существует число Q данное же число существует пока существуют простые числа. Это следует из выражения (1), так как число Q получено путём постоянного перемножения всех простых чисел. А так как простых чисел бесконечно много, то существование числа Q, а вследствие числа Q — 2-будет вечным. А если существует бесконечное (вечное) число Q — 2 то существуют и бесконечные пары простых чисел Р1 и Р2 ДР = 2. А это и есть эквивалент существование бесконечного количества пар простых близнецов. Что и требовалось доказать. То есть чтобы не существовало число Q — 2 необходимо чтобы не существовало число Q, а это не возможно, так как число Q получено путём перемножения всех простых чисел, тогда чтобы его не существовала необходимо не существование простых чисел, или чтобы их было конечное количество, но их существует бесконечное количество, а это значит что число Q существует а значит и существует число Q —2. То есть если рассмотреть выражение (2): 2 х 3 х 5 х 7 х,_,хР = Q(2) Если действие умножение на каждый множитель обозначить за 1-ну секунду то данное число будет существовать вечно, так как простых чисел бесконечное количество. Q-2 Q 2 — 0 — 0 3 1/3 — — 5 1 5 — 3/5 — 0 7 1Л 2 ' 3/7 — 5/7 — 0 И 1/11 2/11 3/11 4/11 5/11 6/11 7/11 — 9/11 — 0 13 1/13 2/13 3/13 4/13 5/13 6/13 7/13 8/13 9/13 — 11/13 — 0 Р 1/Р 2/Р 3/Р ^/р 5/Р 6/Р (Р -6) /Р (Р -5) /Р (Р -4) /Р — (Р -2) /Р — 0 ТаблицаJ №7 Рис. 5. В таблице №7 будет такая ситуация она существует, пока существует умножение на новые простые числа, а их бесконечно. 2 х 3 х 5 х 7 х,... ,х Р х Р1 х Р2 х Р3 х Р4 х, ... ,х Pr = Q А если Q не существует, тогда значит, нет числа Q + 1, так как получить Q + 1 без числа Q нельзя, но если это так тогда получается разрыв в натуральном ряду в целых числах. То есть это будет противоречить аксиоме индукции: Аксиома индукции. Если некоторое множество натуральных чисел содержит единицу и вместе с каждым натуральным числом, входящим в него, содержит следующее за ним, то оно содержит все натуральные числа. Рис. 6. И натуральный ряд не содержит все натуральные числа, так как не содержит числа Q. Бухштаб стр. 16.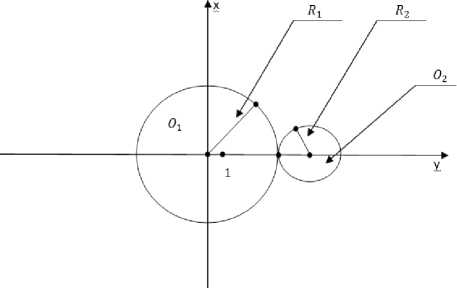

Список литературы Существует бесконечное количество пар простых чисел
- Бухштаб А.А. Теория чисел. 1966. С. 7-48.
- Иен Стюарт. Величайшие математические задачи 2015. С. 225-255.
- Берман Г.Н. Циклоида. 1980.
- Эрнст Трост Простые числа 1959. С. 103.


