Существующие методы расчета резерва запасных элементов

Рассмотрим способы создания резерва.

Нормативное планирование резерва ЗИП к электродвигателям опирается на систему ППРЭсх, по которой годовой ре-

n зерв i запасных частей i - ой номенкла-

туры рассчитывается через годовую норму

H i

расхода запасных частей

i

ой но-

менклатуры на сто изделий и общее количество N изделий данного типа, имею

щихся в эксплуатации:

Методика расчета величины

H i

для

электрооборудования, в сельском хозяй-

стве и в ряде других отраслей промыш-

ленности в технической литературе отсутствует [1, 2]. Существуют методики расче-

та

H

i для отдельных типов сельскохозяй-

ственной техники, разработанные ГОС-

НИТИ [3, 4], также методики расчета

H i

в

Минусами нормативного подхода резервирования запасных элементов считается также его неспособность учитывать конкретные условия эксплуатации электрооборудования для отдельных хозяйств, который выражается в разном спросе на запасные части.

Когда мы создаем резерв запасных элементов, исходя из условия достаточности, принимаем вероятностью того, что в течение всего цикла поставок количество запасных деталей окажется достаточным для замены пришедших в негодность.

При начале расчета указанной вероятности необходимо знать, какой вид имеет плотность распределения времени наработки деталей до отказа и плотность распределения времени вышедшего из строя элемента, в том случае если он после ремонта пополняет резерв.

В большинстве работ [7, 8, 9] предполагается, что наработка до отказа имеет показательное распределение

системах ППР хозяйств промышленных предприятий [5, 6].

f ( t ) = Я ехр ( - Я / )

где

f (t)

плотность распределения

времени наработки деталей до отказа;

Я -

интенсивность отказов, т. е. среднее число отказов в единицу времени ( ^Я = const ); t - время работы до отказа.

В отраслевой методике энергетической промышленности [10] рассмотрены две ситуации:

– Неисправная единица оборудования выводится в ремонт, и вместо нее устанавливается взятая из резерва. Неисправная единица после ремонта пополняет резерв.

– Резерв изделий рассчитывается на определенный промежуток времени, к концу которого желательно иметь минимум этих изделий. Пополнение запаса на фиксированном промежутке времени не предусматривается.

В случае один задаются вероятностью

P(Nn)

^р задержки в удовлетворении требований на изделия резерва. Указанная вероятность выражается через среднюю интенсивность требований на изделия из резерва - ^Я , среднюю интенсивность пополнения резерва отремонтированными изделиями – A                    ^N

, количеством изделий резерва – ^р по формуле

P ( N p ) = 1

^

У 1 <  я

2^J Np! IA J

exp

^

я )

A J

.

Зная ^р и с помощью приведенной в [10] номограммы определяют N р

.

В случае два

P (N,)

^р нехватки

задаются вероятностью

ется через среднее ожидаемое количество требований на фиксированном отрезке N времени – ср , количество изделий в ре-

N зерве – р по формуле

запаса, которая выража-

^{P ( N}p )

N р _N ^{N р}

= ^{1 -} Е 7 7 7 ^ex p^(- N ср ) 0 N Р ^!

.

Зная P ⁽ N P )

N и ср ,по приведенным

NP / N=p таблицам находим     р ср , арифметическим путем выражаем откуда

N р

.

Обратим внимание, что хотя в [10] и отсутствуют прямые указания на то, что выражения (2) и (3) были получены исходя из показательного распределения времени наработки деталей до отказа, но вид формул совпадает с видом аналогичных выражений, показанными другими авторами [8, 9] которые использовали именно распределение.

Cотсков в [9] предлагает методику расчета резерва для изделий, состоящих из однотипных элементов, каждый из которых имеет интенсивность отказов, равную Я i . В этом случае результирующая интенсивность будет

Я рез = N Я i .

Предположим, что отказавший элемент не восстанавливается, а вместо него каждый раз будет вводиться в систему новый элемент, взятый из запаса. В этом случае для замены отказавших элементов необходимо число запасных элементов z = n = Л t ср            рез

.

Этому среднему числу будет соответствовать    гарантийная    вероятность

P = 0,5 того, что за время t не понадобится большее число запасных элементов. Для случая P > 0,5, когда количество z п > zrn запасных деталей в резерве р ср , приводятся номограмма, из которой можно определить требуемое zР , в зависимости от гарантийной вероятности безотказной работы P и величины ср .

Все вышеизложенные методы расчета вероятности безотказной работы основаны на том, что наработка элемента на отказ, описывается показательным законом (1). Согласно [8] показательное распределение применяется чаще других при исследовании надежности изделий.

В настоящее время, все большее распространяется создание резерва запасных элементов, основываясь на междисциплинарной области знаний – теорию управления запасами [11, 12, 13].

В реальных условиях рыночных отношений главное значение имеет экономический фактор. Теория управления запасами начинается с экономической оптимальности организации системы закупок, хранения запасных частей, доставки и постоянное обеспечение потребителей.

При этом мы имеем два аспекта проблемы. Закупка чрезмерного количества запасных частей связана с необоснованно большими затратами на их покупку, хра- нение, возможным омертвлением денежных средств, вложенных в не требуемые за время между поставками запасные части, а недостаток запаса может привести к простою и необеспеченности потребителя. Задача усложняется тем, что спрос на запасные детали случайная величина, зависящая от множества случайных факторов.

Нахождение оптимального компромисса в финансовом плане, между указанными противоборствующими требованиями в каждом конкретном случае и является одной из основных задач в теории управления запасами.

Рассмотрим самую простую модель, в которой пополнение склада продуктом производится до фиксированного объема через фиксированные промежутки времени, и приняв, что спрос на продукт является определенным, и интенсивность спроса – постоянна, Уилсон получил выражения для идеального периода T , оптимального уровня пополнения склада n , и для затрат на запасы в единицу времени L .

T =

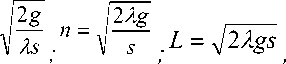
где ^ - интенсивность спроса, g -цена поставки, s – цена хранения продукта в единицу времени.

Следует обратить внимание, что несмотря на большое количество публикаций теория управления запасами еще не сложилась как самостоятельная дисциплина. Разработкой ее основ занимались специалисты самых различных профилей: экономисты, инженеры, математики. Этим обусловлено различие стилей подходов и даже терминологии.

Для оптимизации резерва запасных элементов необходимо выполнение работ по следующей методике [6]. Статистическим путем установить P ( i ) , ^Т и t ^в ; по данным электротехнической службы птицеводческого хозяйства установить ^ и ^ А С„ ^j ; по данным бухучета установить ⁿ ,

C

, ⁰ ; на основе выражений, произвести расчет параметров m и n резерва запасных элементов основной и смежной номенклатур. При практическом определении оптимальных m и n можно пользоваться разработанной и представленной в [14] номограммой.

Таким образом, для реализации разработанной методики оптимизации запасных частей электрооборудования, необходимо выполнение следующего: статистическим путем оценить распределение требований на запасные части; в зависимости от конкретных условий выбрать функцию общих издержек на запасы и на основании данных электротехнической службы и бухгалтерского учета определить её параметры; затем используя программное обеспечение, расчетные формулы или номограмму, определить оптимальное количество за- пасных частей [14].