Связанная модель флюидонасыщенных пористых материалов, основанная на совмещении дискретного и континуального подходов

Многие природные и техногенные материалы и среды, такие как проницаемые горные породы (в том числе угольные и нефтеносные пласты) [1, 2], костная ткань [3], фильтрующие материалы, эндопротезы и т.д., представляют собой пористые или трещиновато-пористые флюидонасыщенные среды. Механический отклик проницаемых флюидонасыщенных материалов характеризуется рядом особенностей, которые отличают его от твердофазных композиционных материалов, в которых фазы также имеют весьма различные упругие и реологические характеристики. Эти особенности связаны со способностью жидкой фазы перераспределяться в трещинно-поровом пространстве вме- щающего материала (макроскопический модуль сдвига жидкости традиционно полагается равным нулю). В результате такого перераспределения могут иметь место выравнивание среднего напряжения в различных областях материала, а также его значительные колебания, связанные с дилатансией и заполнением новых несплошностей, а также с обменом жидкостью с окружающей средой (в случае проницаемых границ).

Общим теоретическим подходом к изучению проницаемых флюидонасыщенных материалов является использование связанных моделей, учитывающих три важнейших аспекта функционирования таких систем: 1) взаимосвязь деформации твердофазного скелета с изменением объема и просветности трещинно-порового пространства; 2) взаимосвязь порового давления и напряжений во вмещающем объеме твердого тела; 3) процессы перераспределения флюида в трещиннопоровом пространстве. Наиболее известными представителями этого подхода являются аналитические макроскопические модели пороупру-гости, теоретические основы которых были заложены в работах Био [4–6]. Дальнейшее их развитие связано с учетом многомасштабности реальных материалов, процессов накопления повреждений, дилатансии и их влияния на упругие свойства каркаса и поровое давление флюида [7–10]. Возможности указанных и аналогичных макроскопических связанных моделей, как правило, ограничены проведением оценок напряженно-деформированного состояния проницаемых материалов (в первую очередь геологических) в стационарных условиях. При этом «за кадром» остается важный класс проблем, связанных с нестационарными и переходными процессами при динамическом нагружении, динамическом изменении граничных условий или разрушении. Основным инструментом теоретического решения подобных задач является численное моделирование с привлечением различных связанных моделей на основе концепции пороупругости.

В настоящее время численное моделирование флюидонасыщенных проницаемых материалов осуществляется преимущественно с использованием методов механики сплошных сред (методов конечных элементов и конечных разностей) [11–22]. Это связано в первую очередь с возможностью реализации в рамках этих методов различных реологических (в том числе связанных и многоуровневых) моделей твердых тел и изучения механического отклика материалов на различ- ных масштабных уровнях. Несмотря на очевидные и известные достоинства подхода сплошной среды, в его рамках затруднено изучение процессов во флюидонасыщенных материалах и средах, сопровождающихся множественным разрушением твердого каркаса и контактным взаимодействием образующихся поверхностей.

Указанные ограничения при моделировании разрушения не присущи вычислительным методам, относящимся к дискретной концепции представления среды [23–28]. Известным представителем данного класса методов является метод дискретных элементов (МДЭ), в рамках которого моделируемый материал представляется ансамблем взаимодействующих частиц конечного размера [29–34]. Основные его преимущества связаны со способностью дискретных элементов изменять окружение, что является принципиально важным при моделировании сложных явлений контактного взаимодействия, трещинообразования и разделения тел на фрагменты и т.д.

Несмотря на это, область применения традиционных реализаций МДЭ для численного решения задач механики флюидонасыщенных материалов, как правило, ограничивается микроскопическим масштабным уровнем, на котором поры, трещины и каналы учитываются явным образом. При этом широко используются комбинированные схемы, в которых МДЭ применяется для моделирования механического отклика твердофазного каркаса, а метод решеточных уравнений Больцмана, или метод сеток, – для моделирования течения слабосжи-маемых жидкостей [35–39]. В то же время возможности использования МДЭ для моделирования отклика проницаемых материалов на более высоких масштабных уровнях являются весьма ограниченными ввиду недостаточного развития математического формализма данного метода для адекватного описания многомасштабных систем. В частности, одним из широко распространенных недостатков существующих реализаций МДЭ является применение парного приближения при описании взаимодействия дискретных элементов, что затрудняет моделирование сред со сложной реологией, в том числе упруго-пластических.

Авторами предложен подход к описанию механического отклика многомасштабных флюидонасыщенных упруго-пластических сред в рамках МДЭ, основанный на использовании многочастичного приближения при построении соотношений для сил межэлементного взаимодействия [40, 41].

Ранее на примере изотропных материалов было показано, что использование предложенных соотношений делает возможным реализацию в рамках МДЭ различных моделей и критериев упругости, пластичности и прочности (в том числе макроскопических моделей пластичности горных пород). Дальнейшее развитие предложенного формализма позволило расширить область применения МДЭ на широкий спектр пространственных и структурных масштабов, а также предложить комбинированный численный метод для изучения проницаемых сред на мезо- и макроскопическом масштабных уровнях. Данный метод получил название гибридного метода клеточных автоматов (ГКА). В методе ГКА механический отклик вмещающего твердого тела описывается методом дискретных элементов, а процессы фильтрации и диффузии флюида в трещинно-поровом пространстве (учитываемом неявно) - методом конечных разностей. Отметим, что ранее в рамках метода ГКА была развита связанная модель газоносных материалов [42-44].

В настоящей работе предложена и реализована в рамках метода ГКА связанная макроскопическая модель трещиновато-пористого хрупкого материала, насыщенного жидкостью. Данная модель учитывает взаимовлияние процессов деформирования твердофазного скелета и перераспределения жидкости в поровом пространстве. Возможности метода продемонстрированы на примере параметрического исследования зависимостей прочности упруго-хрупких флюидонасыщенных материалов от размеров пор, геометрии образца и скорости деформирования.

1.    Формализм метода гибридных клеточных автоматов

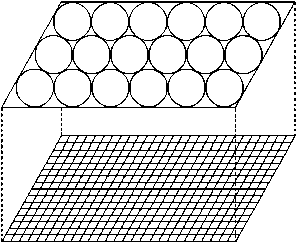
Основу метода ГКА составляет декомпозиция решаемой задачи на две подзадачи: 1) описание механического поведения вмещающего твердого тела (каркаса) и 2) описание переноса жидкости в фильтрационном объеме, представленном системой взаимосвязанных каналов, пор, трещин и т.д. Для описания механического поведения вмещающего тела используется метод подвижных клеточных автоматов (ПКА), развиваемый авторами и являющийся одной из реализаций метода дискретных элементов [40, 41]. В рамках метода ПКА размеры и форма дискретных элементов могут изменяться в процессе деформирования. В зависимости от особенностей структуры рассматриваемого про- ницаемого материала и моделируемого масштабного уровня размеры дискретных элементов могут значительно превышать линейные размеры несплошностей, быть сопоставимыми с ними или меньшими. Влияние «микропор» твердого каркаса (т.е. пор, каналов и других несплош-ностей, характерный размер которых меньше размера частицы) на механические свойства и отклик дискретного элемента учитывается неявно. Также в рамках метода ПКА решается задача фильтрационного переноса жидкости в связанной сети «микропор» вмещающего твердого тела. В то же время вычисление массопереноса жидкости между «микропорами» и «макропорами» (которые рассматриваются как области между пространственно разнесенными и невзаимодействующими частицами) осуществляется на более мелкой сетке, «вмороженной» в лабораторную систему координат (рис. 1, а). Эта же сетка используется и для расчета объемов «макропор».

Модель механического отклика флюидонасыщенного твердого каркаса

Метод ПКА, использующийся для моделирования деформирования и разрушения твердофазного каркаса, относится к группе методов однородно деформируемых дискретных элементов (в английской терминологии – simply deformable discrete element method) [30, 45–47], в рамках которых используется приближение однородного распределения напряжений и деформаций в объеме элемента. Для моделирования отклика трещиновато-пористых хрупких материалов в рамках метода ПКА реализована модель пластичности горных пород с неассоциированным законом течения и критерием Мизеса–Шлейхера достижения предела упругости (модель Николаевского) [48, 49]. Выбор данной модели связан с тем, что она адекватно описывает отклик широкого класса хрупких материалов (геоматериалов, керамик) на различных масштабных уровнях с учетом вкладов «нижележащих» структурных масштабов. Особенностью модели Николаевского является постулируемая линейная связь между скоростями объемной и сдвиговой составляющих пластической деформации с коэффициентом пропорциональности Λ , называемым коэффициентом дилатансии.

Адаптация модели Николаевского к методу ПКА осуществлена с использованием алгоритма Уилкинса [50]. В рамках этого алгоритма решение упруго-пластической задачи сводится к решению упругой за- дачи в приращениях и последующей корректировке потенциальных сил взаимодействия частиц с соблюдением необходимых требований модели Николаевского, предъявляемых к величинам локального давления и девиатора напряжений [49].

Подвижные клеточные автоматы

Конечно-разностная сетка

а

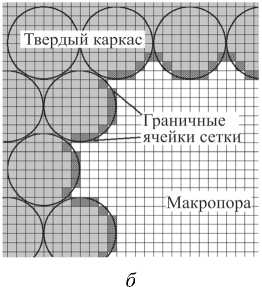
Рис. 1. Слои, образованные дискретными элементами (подвижными клеточными автоматами) и конечно-разностной сеткой ( а ); ячейки сетки на границе твердого каркаса и макропоры ( б )

Решение упругой задачи на ансамбле частиц сводится к определению приращений центральной и тангенциальной компонент силы упругого отклика подвижного клеточного автомата i на воздействие со стороны соседнего автомата j . Соответствующие выражения записываются на основе обобщенного закона Гука в гипоупругой форме [41]:

Ao, . = AF^ t Ss„ = 2 G Ae, . + 1 - ^{1 (} j )               i ⁽ j ) / ^ij i       i ⁽ j )

V

At., = A F ;ang / S.. = 2 G, Ay., i ⁽ j )             i ⁽ j ) / i i i ⁽ j ) ^,

2G )Ki J

mean

^Ao i ,

где символ A означает приращение величины соответствующего параметра за шаг по времени At численной схемы интегрирования; oi(j■) и тi(j■) -удельные значения центральной ( F.centr) и тангенциальной (Fitang ) составляющих потенциальной силы реакции дискретного элемента i на воздействие со стороны соседа j; Sij – площадь поверхности контакта пары; Gi и Ki – модули сдвига и всестороннего сжатия материала элемента i; Aei(j) и Ayi(j) - приращения нормальной и сдвиговой деформации элемента i в паре i-j; О mean - среднее напряжение в объеме эле- мента i. Среднее напряжение о mean вычисляется с использованием соотношения Лява, связывающего компоненты тензора усредненных напряжений (о“в) в объеме дискретного элемента i с силами, действующими на поверхность данного объема [40, 41].

Напряженное состояние проницаемого твердого тела, содержащего связанную систему пор, каналов и трещин, является сложным и обусловлено не только величиной удельного объема несплошностей, но и особенностями их геометрии и пространственного распределения [51]. При отсутствии выраженной геометрии и ориентации (текстуры) трещинно-порового пространства адекватным является приближение, в соответствии с которым на мезо- и макроскопическом масштабных уровнях учитывается только вклад давления внутрипорового флюида в величину гидростатического напряжения в скелете (гидростатическое растяжение). В этом приближении влияние флюида, содержащегося в «микропорах», на механический отклик дискретного элемента может быть учтено посредством следующей модификации соотношения (1) для силы центрального взаимодействия:

Д<5 , л i ( j )

= ДРС™,Г /S„ = 2G Де.м i (j) / j i          i (j)

Д p fluud

< эсЛ

+ 1 - --^ До m

mean

V

М

i

,

где Pi fluid – вклад порового давления флюида в «микропорах» в вели- чину среднего напряжения в объеме дискретного элемента i. Отметим, что выражение (2) аналогично записи закона Гука в линейной модели пороупругости [6].

Величина Pi fluid линейно связана со средним поровым давлением флюида Pi pore в «микропорах» дискретного элемента i:

P i

fluid

= a i P' ⁰ " ,

где a i – безразмерный коэффициент (0< a i ≤1), величина которого связана с характеристиками «микропор» (пористостью, топологией порового пространства, размерами пор и т.д.).

После решения упругой задачи для элемента i на текущем временном шаге проверяется условие достижения предельного состояния (критерий Мизеса–Шлейхера), учитывающее вклад порового давления флюида:

ф,=Р,(»,“ + ърт )+а 'V V3 = Y,

где Y i - предел упругости материала элемента i при сдвиге; P i - коэффициент внутреннего трения; о eq - интенсивность усредненных напряжений в объеме элемента i ; b i – безразмерный коэффициент. Ввиду конечной величины шага интегрирования уравнений движения A t фактически проверяется условие Ф i >  Y i . При его выполнении осуществляется приведение тензора усредненных напряжений о “^в в объеме дискретного элемента i к предельной поверхности. Как показано в [41], такое приведение реализуется путем корректировки удельных значений сил центрального и тангенциального взаимодействия элемента i с соседями j :

т‘ = т, Mf

*⁽ j )           *⁽ j ) ¹

N't ,

где ( o’ ( j ) , т‘ ( j ) ) - приведенные значения удельных сил реакции автомата; M i = 1 - ( V3/ о^ ) ( 3 G i ( Ф i - Y )/( K i Л i в i + 3 G i ) ) - коэффициент приведения девиаторов напряжений; N i = K .. Л . ( Ф . - Y i )/( K i. ЛД + G i ) -поправка к величине среднего напряжения, вычисленного в упругом приближении; Л i - коэффициент дилатансии материала автомата i .

Под влиянием напряжений в твердом каркасе изменяется объем вмещающего твердого тела и, соответственно, объем связанной системы несплошностей (именуемой также открытой пористостью или фильтрационным объемом). Удельный объем связанной системы «микропор» характеризуется величиной «микропористости» ф . В рамках предложенной модели связь между открытой микропористостью дискретного элемента i и его объемной деформацией устанавливается следующим образом:

ф . =ф 0 ( 1 + c i ^ elast ) +^ Plast ,

где ф0 и ф. - начальное (при нулевом давлении в каркасе) и текущее значения открытой микропористости; c – безразмерный коэффициент пропорциональности (ci>1); Qfast и Q"la's — упругая и пластическая составляющие объемной деформации элемента, определяемые следующим образом:

<

elast

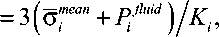
q plast

= ( e xx + E yy + e ^zz ) -Q ^e1 ^ast .

Здесь E ““ - диагональные компоненты тензора усредненных деформаций в объеме дискретного элемента I [40, 41].

Уравнения (2)-(7) составляют математическую формулировку модели взаимодействия твердого каркаса и жидкого флюида в «микро-поровом» пространстве, реализованной в рамках метода гибридных клеточных автоматов. Важным вопросом при использовании этой модели является определение значений безразмерных коэффициентов ai, bi и ci для изучаемого материала. Одним из вариантов такого определения для коэффициентов ai и ci является использование линейной модели пороупругости Био [6]. В этом случае коэффициент ai соответствует экспериментально определяемой константе а скорости изменения удельного объема жидкости при деформировании вмещающего твердого тела, а коэффициент ci - константе а для частично заполненных жидкостью пор либо произведению (B/Ku/Kf), где B - коэффициент Скемптона, Ku и Kfl - модули всестороннего сжатия флюидонасыщенного материала и флюида. Следует отметить, что такое определение коэффициентов ai и ci может рассматриваться как оценка сверху. Оценкой снизу является приближение ai = фi и ci =1, которое становится адекватным в случае малых значений «микропористости» и «микропор» наноскопического масштаба [52]. Величина коэффициента bi традиционно полагается равной 1 [53, 54]. Однако необходимо отметить, что такое приближение справедливо для материалов, проницаемость и конфигурация порового пространства которых обеспечивают возможность равномерного распределения гидростатического давления в твердофазном каркасе (здесь также действует условие химически нейтральной жидкости) [55, 56]. Неявно здесь используется предположение о том, что образование новых повреждений (с которыми и связана макроскопическая квазипластичность хрупких материалов) привязано непосредственно к сети существующих микропор. В то же время особенности порового пространства и микроскопической структуры твердофазного каркаса могут определять более сложную связь между поровым давлением и накоплением повреждений, в которой величина bi меньше 1 и является функцией параметров пористости и соотношения приложенного и порового давлений [52, 53, 56, 57–59]. В качестве нижней границы параметра bi может рассматриваться величина пористости φi [53].

Развитый подход к построению многочастичного взаимодействия дает возможность использовать многопараметрические критерии разрушения (Кулона–Мора, Друккера–Прагера и т.д.) в качестве критерия разрыва химической связи (потери сцепления) в парах взаимодействующих дискретных элементов [41]. В представленных далее результатах численного моделирования применяется модифицированный критерий разрушения Друккера–Прагера, учитывающий вклад локального порового давления флюида аналогично (4):

о DP = 0,5 ( 1 + 1 ) о eq + 1,5 ( X- 1 ) ( о mean + bP p" ) = о c , (8) где 1 = о c /о t - отношение прочностей сцепления пары элементов при одноосном сжатии ( о _c ) и растяжении ( о t ), коэффициент b соответствует тому же в соотношении (4). Детальное описание расчета критерия прочности для пар связанных дискретных элементов приведено в работах [40, 41]. Отметим, что, хотя критерии наступления неупругой деформации (4) и разрушения (8) имеют одинаковую структурную форму, смысл коэффициентов при слагаемом о mean в них различный. Так, величина коэффициента в в (4) определяет степень влияния давления на зарождение и развитие сети микроскопических повреждений и трещин в объеме материала. В то же время коэффициент 1,5 ( 1- 1 ) определяет влияние давления на условие локализованного объединения отдельных микроповреждений в единый мезо- или макроразрыв. Сказанное свидетельствует о том, что значения этих двух коэффициентов не обязательно являются согласованными, поскольку роль локального давления в эволюции повреждения, как правило, существенно возрастает с ростом пространственного масштаба повреждения.

Уравнение состояния и модель фильтрационного переноса жидкости

В рамках развитой модели переноса жидкости используются следующие приближения: 1) жидкость может занимать объем поры как полностью, так и частично; 2) жидкость считается сжимаемой; 3) адсорбция жидкости на стенках пор, капиллярные эффекты и эффект адсорбционного понижения прочности проницаемого твердого тела не учитываются; 4) распределение «микропор» (то есть связанных между собой несплошностей в объеме дискретных элементов) по размерам не учитывается. Отметим, что в рамках последнего приближения трещинно-поровое пространство дискретного элемента описывается двумя параметрами: величиной открытой «микропористости» ф и характерным диаметром фильтрационного канала d ch . Важно отметить, что величина d ch в общем случае равна не среднему поперечному размеру несплош-ностей, но размеру наименьших сужений в поровом пространстве, определяющих скорость фильтрации жидкости через проницаемый объем дискретного элемента. При корректном определении параметра d ch описанное упрощение при описании трещинно-порового пространства является адекватным для широкого класса проницаемых материалов, включая геоматериалы [60].

В развитой модели сжимаемая жидкость описывается следующим уравнением состояния [61]:

р ( P ) = Р о ( 1 + ( P - P ) / K , ) ,                     (9)

где р и P - текущие значения плотности и давления жидкости; р ₀ и P 0 -значения плотности и давления жидкости при атмосферных условиях; K fl – модуль всестороннего сжатия жидкости. Важной особенностью жидкости является ее способность частично занимать объем предоставленного порового пространства (в то время как газ занимает предоставленный объем целиком). Когда жидкость заполняет объем поры лишь частично, ее давление на твердый каркас может полагаться равным нулю (фактически давление определяется в этом случае весом жидкости, которым в рамках данной модели пренебрегаем). Соответственно, если отношение массы жидкости в поре к объему занимаемой поры меньше р ₀, ее давление полагается равным значению P 0 .

Соотношение (9) определяет связь между плотностью и давлением жидкости как в «макропорах» (учитываемых явным образом как области между поверхностями несвязанных дискретных элементов), так и «микропорах» в объеме дискретных элементов. В последнем случае предполагается, что проницаемость и конфигурация «микропоро-вого» пространства дискретного элемента обеспечивают возможность равномерного распределения гидростатического давления в его твердофазном каркасе. Это позволяет оперировать для каждого дискретного элемента i усредненными по его объему значениями плотности ρ i и порового давления P_i ^pore содержащегося флюида (данное приближение отвечает формализму метода однородно деформируемого дискретного элемента).

При моделировании фильтрации используется предположение об определяющей роли градиента давления жидкости как движущей силы этого процесса. В пренебрежении гравитационными эффектами уравнение фильтрации (переноса плотности жидкости) в «микропоровом» пространстве твердого тела может быть записано следующим образом [61]:

∂ρ

»l⁼K« ^v I n ^v p ,

∂ t

где η – вязкость жидкости; k – коэффициент проницаемости твердого каркаса, который может быть определен следующим образом [62]:

k =ϕ d c ² h . (11)

Уравнение (10) численно решается на сетке дискретных элементов методом Эйлера. Отметим, что с учетом используемых приближений массоперенос между узлами сетки, в которых ρ ≤ ρ 0 , отсутствует.

Используемые в предложенной модели приближения подразумевают пренебрежение массопереносом жидкости между дискретными элементами за счет капиллярных сил. Для большинства горных пород это является справедливым в случае «микропор», характерный размер которых d ch не превышает первых микрометров. При больших значениях d ch «капиллярный» вклад в фильтрацию может учитываться отдельным соотношением.

Моделирование массопереноса между микро-и макропорами

При описании твердого каркаса как ансамбля частиц возникает задача определения объемов макроскопических пор и полостей в твердом каркасе, а также вычисление протяженности границ раздела между твердым каркасом, содержащим микропоры, и макропорами. Как отмечалось выше, под макропорой (полостью) в данной модели понимается пора, размер которой больше размера подвижного клеточного автомата (дискретного элемента твердого каркаса). Для определения расположения и размеров макропор система дискретных элементов проецируется на конечно-разностную сетку (см. рис. 1, б ). Далее, для расчета переноса жидкости на границе «твердофазный скелет– макропора» определяются узлы сетки, принадлежащие подвижным клеточным автоматам и граничащие с узлами, принадлежащими макропорам. Количество таких узлов для каждого подвижного автомата определяет протяженность границы его контакта с макропорой (либо с несколькими макропорами). Расчет переноса жидкости между макропорами и граничащими с ними подвижными клеточными автоматами, содержащими в своем объеме микропоры, осуществляется на основе уравнения (10).

Для описания перераспределения жидкости в объеме одной макропоры или между соединяющимися макропорами в работе используется приближение равного давления. В рамках данного приближения полагается, что в замкнутом макрообъеме на каждом шаге интегрирования плотность и давление жидкости распределены однородно. Такое упрощение является адекватным при низких скоростях процессов и в случае частично заполненных жидкостью макрообъемов. Отметим, что в более общем случае моделирование процессов массопереноса жидкости в системе соединяющихся макропор может осуществляться, например, с использованием метода решеточных уравнений Больцмана.

Верификация построенной модели проводилась на основе следующих тестов: 1) просачивание жидкости через тонкий слой и 2) выдавливание жидкости из образца при медленном нагружении (без разрушения). Результаты, получаемые в численных расчетах, отличались от соответствующих аналитических оценок для профилей давления, времени установления стационарного режима фильтрации и остаточного количества жидкости в образце не более чем на 1 %.

2.    Изучение прочности пористых флюидонасыщенных образцов упруго-хрупкого материала при одноосном сжатии

Развитая модель была применена для моделирования одноосного сжатия пористых образцов, фильтрационный объем которых заполнен водой. Образцы были закреплены между неподвижной матрицей (снизу) и пуансоном (сверху), который двигался вниз, сжимая образец с постоянной скоростью V y . Направление сжатия совпадало с вертикальной осью образца (рис. 2, а ).

а

Деформация

б

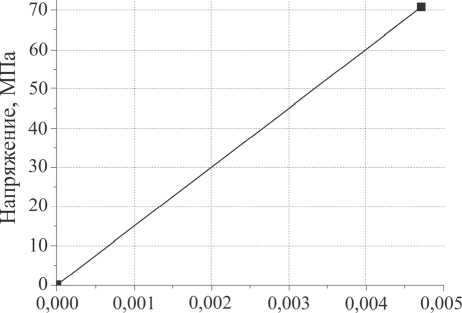
Рис. 2. Схема нагружения моделируемого образца ( а ), диаграмма одноосного сжатия модельного упруго-хрупкого материала образца ( б) (точкой на рис. ( б) отмечено значение о c )

Задача решалась в двумерной постановке в приближении плосконапряженного состояния. Структура образца полагалась однородной, макроскопические поры и включения отсутствовали. Свойства модельного материала образца соответствовали свойствам песчаника, диаграмма одноосного сжатия модельного материала приведена на рис. 2, б . В проведенных численных экспериментах были использованы следующие значения параметров модельного материала: К = 37,5 ГПа, G = 5,77 ГПа, р = 2000 кг/м³, о _c = 70 МПа, X = 7, a = ф = 0,1, с = 1, К = 2,2 ГПа, значение параметра b варьировалось в пределах от b = ф = 0,1 до b = 1. Высота образца H = 0,1 м, ширина образца W = 0,05 м.

Результаты моделирования выявили существенное влияние порового давления жидкости на механический отклик хрупких пористых образцов, при этом имеющее более сложный характер, чем влияние давления газа в порах [44]. Помимо порового давления, на прочность образцов оказывают влияние такие факторы, как скорость нагружения, характерный диаметр фильтрационного канала (величина, совместно со значением открытой пористости характеризующая проницаемость материала) и геометрические размеры образца.

В условиях одноосного сжатия давление жидкости в порах твердого тела определяется конкуренцией двух процессов: 1) деформированием твердого каркаса, сопровождающимся уменьшением объема порового пространства в соответствии с (6)–(7), и ростом порового давления (и, следовательно, усилением влияния жидкости на величину напряжений в каркасе); 2) фильтрацией жидкости во внешнее пространство через боковые поверхности образца, приводящей к уменьшению порового давления и влияния жидкости на напряженное состояние каркаса.

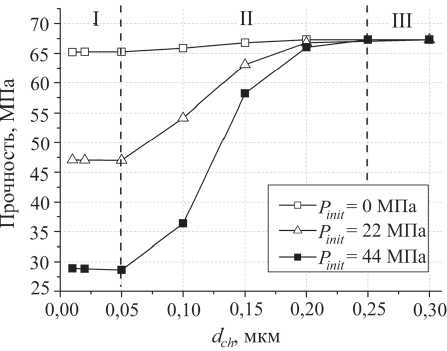
Рис. 3. Зависимости прочности образцов модельного упруго-хрупкого материала при их одноосном сжатии от среднего диаметра фильтрационного канала при различных давлениях жидкости. Переменная P init в легенде обозначает начальное давление жидкости в порах твердого каркаса. Скорость нагружения во всех случаях составляла

V_y = 0,1 м/с

Баланс этих двух процессов связан, в частности, с величиной коэффициента проницаемости материала, определяемого характерным диаметром фильтрационных каналов dch . Так, на рис. 3 приведены полученные путем компьютерного моделирования зависимости прочно- сти образцов модельного материала от величины dch для различных начальных значений порового давления жидкости Pinit. Можно видеть, что приведенные зависимости характеризуются наличием трех участков. На участке I (при достаточно низкой проницаемости образцов) отток жидкости из образца не компенсирует увеличение ее плотности в процессе деформирования пор. Вследствие этого по мере деформирования давление содержащейся в фильтрационном объеме жидкости постоянно возрастает, что приводит к снижению эффективной прочности образца (4). При больших значениях dch (участок III) обеспечивается скорость оттока жидкости из образца, достаточная для падения порового давления до атмосферного. Влияние жидкости на напряженное состояние таких образцов практически отсутствует, а их прочность стремится к прочности «сухого» образца. На переходном участке II скорость истечения жидкости из образца сопоставима со скоростью увеличения ее плотности.

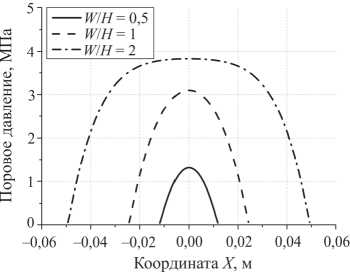
Очевидно, что прочность образцов определяется, в том числе, распределением давления жидкости в поровом пространстве по сечению образца, которое, в свою очередь, зависит от отношения ширины образца W к его высоте H . Зависимость прочности образцов от d_ch при различных соотношениях W / H наглядно иллюстрируется результатами, приведенными на рис. 4, а . Как видно из данного рисунка, с увеличением ширины образца зависимость прочности от среднего диаметра фильтрационного канала становится более пологой. Иными словами, с увеличением соотношения W / H влияние внутрипоровой жидкости на величину прочности образца усиливается. Данный эффект объясняется следующим образом. С увеличением ширины образца доля материала, примыкающего к боковой поверхности и, соответственно, более подверженного оттоку жидкости во внешнее пространство, снижается, как видно из распределений порового давления в горизонтальном сечении образца (рис. 4, б ). Соответственно, удельное количество и давление жидкости, остающееся в порах к началу разрушения, возрастает с увеличением соотношения W / H . Как следует из рис. 4, начиная с некоторого критического (достаточно большого) значения отношения W / H влияние проницаемости на прочность образцов становится несущественным, а значение прочности стремится к нижнему пределу (т.е. к прочности насыщенного жидкостью образца в отсутствие фильтрационного перераспределения жидкости при d_ch → 0).

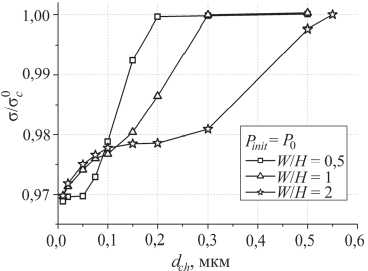
а

Рис. 4. Зависимости прочности образцов модельного упруго-хрупкого материала при их одноосном сжатии от среднего диаметра фильтрационного канала при различных значениях ширины W образца ( а ) и распределения порового давления в горизонтальном сечении образцов различной ширины к началу разрушения ( б ). Во всех случаях

V y = 0,1 м/с, P init = P 0

б

Обобщенное выражение для прочности образца упруго-хрупкого флюидонасыщенного материала при одноосном сжатии

Как было отмечено выше, прочность флюидонасыщенных образцов при их одноосном сжатии определяется конкуренцией процессов механического деформирования образца под действием приложенной внешней нагрузки и оттока жидкости из порового пространства во внешнюю среду. Для выявления общих закономерностей такой конкуренции проведено детальное изучение влияния скорости нагружения на прочность образцов, насыщенных жидкостью. Моделировалось одноосное сжатие насыщенных жидкостью образцов, характеризующихся различными значениями d_ch , с различными скоростями нагружения V y . Начальное поровое давление жидкости P init полагалось равным атмосферному давлению (поровое пространство образцов полностью заполнено жидкостью). Рассматривались два приближения при учете влияния порового давления на прочность твердофазного каркаса.

• 1.    Микропоры распределены однородно, размер их много меньше характерного размера формирующихся в процессе разрушения повреждений. В таком случае при относительно небольших значениях пористости можно полагать, что возникновение повреждений жестко не привязано к местам расположения микропор и в большей степени определяется наличием в твердом каркасе других дефектов большего (в сравнении с микропорами) масштаба. При этом влияние поровой

• 2.    Микропоры распределены неоднородно, повреждения в материале формируются путем соединения трещиной нескольких микропор. В этом случае влияние поровой жидкости на прочность каркаса определяется непосредственно величиной порового давления: b = 1.

жидкости на прочность каркаса определяется величиной пористости и учитывается посредством следующего определения коэффициента b в (8): b = φ.

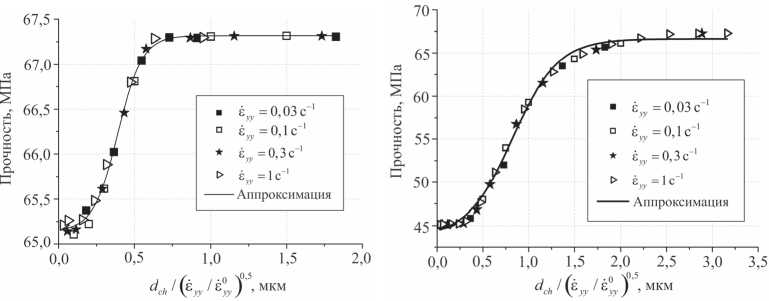
На рис. 5 приведены зависимости прочности образцов от характерного диаметра фильтрационного канала при различных скоростях деформации. Можно видеть, что значение параметра b , определяющего вклад порового давления в критерии пластичности (4) и разрушения (8), оказывает значительное влияние на прочность флюидонасыщенных образцов. Так, в случае использования приближения однородного распределения микроскопических пор ( b = φ = 0,1, рис. 5, а ) в твердом каркасе вклад порового давления оказывается достаточно слабым (максимальное снижение прочности образцов не превышает 3 %). В рамках второго приближения ( b = 1, рис. 5, б ) вклад порового давления в прочность образцов возрастает на порядок величины, а величина предельной деформации снижается. При этом имеет место «выполажи-вание» зависимостей прочности от диаметра фильтрационного канала, обусловленное более сильным влиянием остаточной жидкости в поровом пространстве на прочность образцов.

а б

Рис. 5. Обобщенная зависимость прочности водонасыщенных образцов от диаметра фильтрационного канала при различных скоростях нагружения: а – приближение однородного распределения микроскопических пор ( b = φ = 0,1); б – приближение относительно крупных микропор, развитие которых определяет формирование макротрещин ( b = 1). Начальное давление жидкости в порах твердого каркаса P_init = P ₀

Анализ полученных зависимостей прочности образцов от эффективного диаметра фильтрационных каналов dch при различных скоростях нагружения показал возможность сведения их в единую кривую зависимости прочности от приведенного диаметра фильтрационного канала doh/£,„/60, , (12)

где £ _yy = V_y / H - скорость деформации; £ 0 y - масштабный множитель, имеющий размерность скорости деформации. Кривые, показанные на рис. 5, построены в указанных переменных.

Зависимости прочности от приведенного диаметра (см. рис. 5) могут быть аппроксимированы аналитическим выражением следующего вида:

min 0

O c ( d_ch , ^£ yy ) = О 0 c " c , (13) 1 ⁺ exp ( ( d ch - d 0 ) / d c yy /^£ yy )

где О С - прочность образца при одноосном сжатии в отсутствие жидкости в поровом пространстве; О min - прочность водонасыщенного образца в условиях «запирания» жидкости в порах (т.е. при отсутствии фильтрационного движения жидкости в твердом каркасе); d ₀ и d_c – параметры аппроксимирующей зависимости, имеющие размерность расстояния и характеризующие соответственно положение и ширину переходного участка зависимости прочности от характерного диаметра фильтрационных каналов. Величина О min может быть оценена на основе соотношений (6)–(8) следующим образом:

О min

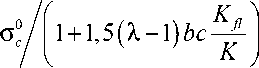
Как следует из выражения (14), на прочность флюидонасыщенных образцов оказывают влияние не только прочностные свойства твердого каркаса, но и свойства жидкости, находящейся в поровом пространстве, а также характер пористости и удельный вклад порового давления в напряженное состояние каркаса. Для использованных в на- стоящих расчетах параметров материала твердого каркаса и жидкости оценка σcmin составляет 63,92 МПа для b = 0,1 и 44 МПа для b = 1, что хорошо согласуется с результатами моделирования для dch →0 (см. рис. 5). Заметим, что оценка (14) дает немного заниженные значения прочности в связи с тем, что в ней не учитывается влияние порового давления жидкости на изменение объема пор.

В целом сложный характер взаимосвязей между параметрами, характеризующими механический отклик твердого каркаса, физикомеханические свойства жидкости и динамику ее фильтрационного перераспределения в системе пор, определяет нелинейную зависимость прочности образцов от совокупности данных параметров и обусловливает необходимость применения численных методов для изучения отклика пористых флюидонасыщенных образцов и материалов.

Заключение

В работе рассмотрен подход к моделированию пористого материала, насыщенного жидкостью. В рамках данного подхода, названного методом гибридных клеточных автоматов, рассматриваемая среда моделируется как суперпозиция двух взаимосвязанных слоев, один из которых представлен ансамблем частиц (подвижных клеточных автоматов), а другой – конечно-разностной сеткой. Развитый подход позволяет явным образом учитывать как деформацию и разрушение твердого каркаса, так и перераспределение жидкости в поровом пространстве и в макроскопических полостях.

Развитый в работе формализм применен для параметрического исследования зависимостей прочности упруго-хрупких флюидонасыщенных материалов от размеров пор, геометрии образца и скорости деформирования. Показано, что прочность упруго-хрупких образцов, насыщенных водой, при одноосном сжатии существенным образом зависит не только от свойств материала и давления жидкости в поровом пространстве, но и от размера пор, физико-механических свойств жидкости и геометрических размеров образца. Построена аналитическая зависимость прочности флюидонасыщенного образца при одноосном сжатии от указанных параметров, обобщающая результаты численного моделирования.

Приведенные результаты демонстрируют возможности построенной модели, а также показывают важность применения численного моделирования для изучения механических свойств (включая прочность) флюидонасыщенных материалов при динамическом нагружении.

Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук на 2013–2020 годы.