Свободная энергия активации текучести и энергия делокализации атома в силикатных стеклах

А F + RT да

exp

^ А £

( RT

e

- 1

где Δε e – энергия делокализации атома, R – газовая постоянная, Δ F ∞ – потенциал перескока атома (кинетической единицы) в новое положение. Второе слагаемое представляет собой потенциал локального изменения структуры Δ F s ( T ). Можно показать, что эта формула с помощью двух подгоночных параметров Δ F ∞ и Δε e вполне удовлетворительно описывает температурную зависимость свободной энергии активации вязкого течения стеклообразующих расплавов в широком интервале температур [6, 7].

При выводе уравнения (2) предполагается, что вероятность перехода кинетической единицы W из одного равновесного положения в другое определяется, во-первых, вероятностью локального изменения структуры W 1 у данной кинетической единицы и, во-вторых, вероятностью W 2 того, что она обладает достаточной энергией Δ F ∞ для перехода в новое положение: W = W 1 W 2 . Вероятность локального изменения структуры при активации вязкого течения стеклообразующего расплава описывается как вероятность делокализации атома, связанной с перемещениями соседних частиц [5].

Под “делокализацией атома” в неорганических стеклах и их расплавах подразумевается смещение мостикового атома (типа атома кислорода в мостике Si-O-Si), связанное с локальной низкоактивационной вязкоупругой деформацией сетки валентных связей. Необходимым условием делокализации активного атома – его смещения из равновесного положения – является образование вблизи него элементарного флуктуационного объема Δve [8, 9].

Настоящая работа посвящена расчету энергии делокализации атомов при активации вязкого течения в неорганических стеклах (на примерах многокомпонентного листового и свинцовосиликатного стекол).

В уравнении (2) энергия делокализации атома Δε e выступает как константа в тех областях температур, где это соотношение успешно описывает температурную зависимость Δ F η ( T ) [5, 6]. Чтобы убедиться в этом, выразим Δε e из формулы (2)

( А F - А F

А £ = RT ln I --- ^п -------- + 1 e           I RT

и проведем расчет в широком интервале температур. Тем самым мы проверяем справедливость зависимости (2).

Вязкость измерена в Институте химии силикатов (ИХС) РАН, состав листового стекла по анализу (вес.%) [11]: SiO 2 – 72.7; CaO – 8.6; MgO – 3.4; Al 2 O 3 – 1.3; Na 2 O – 13.6; K 2 O – 0.4.

Для расчета Δεe по этой формуле необходимо знать величины ΔFη(T) и ΔF∞. Свободную энергию активации вязкого течения листового стекла определили из известного уравнения Эйринга по экспериментальным данным о вязкости η(T) [10, 11]

∆Fη = RT [lnη(T) – lnη 0 ]              (4)

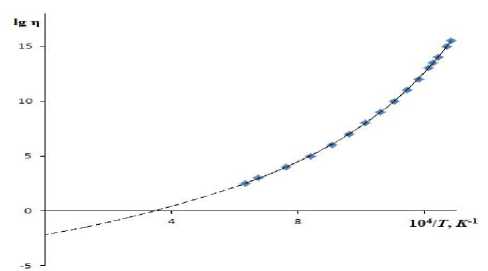
Рис. 1. Температурная зависимость вязкости листового силикатного стекла в координатах lg η – 1/ T . Точки – экспериментальные данные [11], кривая – расчет по уравнению вязкости [5], пунктирные линии – экстраполяция с помощью полинома Лагранжа.

Логарифм предэкспоненциального множителя lg(η 0 , П) = -2.26 находили путем экстраполяции кривой вязкости lg η – 1/ T к повышенным температурам T → ∞ с помощью полинома Лагранжа [12] (рис. 1). Зависимость y = lg η от x = 10⁴/ T описывается полиномом:

Y = - 0.01x3 + 0.04 x2 + 0.55x – 2.26

Величина достоверности аппроксимации: K² = 1.

Потенциал перескока атома ΔF∞    представляет собой высокотемпературный предел свободной энергии активации текучести ΔF∞ = ΔFη (T→∞) и не зависит от температуры. Его можно рассчитать по данным о параметрах C1 и C2 уравнения ВЛФ (Вильямса–Ландела–Ферри) [13], описывающего температурную зависимость вязкости η(T) в области стеклования [10],

ΔF∞= RC1C2

Для проверки применимости соотношения ВЛФ ( a T = η( T )/η( T g ))

T - T lg aT = — C1            „(6)

T — T + C g2

к данному стеклу можно представить его в виде уравнения прямой

— (T-T^J = T — T )+ C^ lg aT C1

и построить график в координатах: –(T – Tg)/lgaT – (T – Tg). Логарифм вязкости lg(ηg, П) = 13.82, соответствующий температуре стеклования Tg = 807 K, получили аппроксимацией кривой lgη – T выражением lgη = 357347002.63 T-2.55

Как видно из рис. 2, зависимость –( T – T g )/lg a T от ( T – T g ) оказывается линейной, что подтверждает справедливость уравнения ВЛФ применительно к листовому силикатному стеклу в достаточно широком интервале температур. Для этого стекла значения параметров уравнения ВЛФ, определенные из рис. 2, равны: C 1 = 36.2, C 2 = 304.6 K , откуда потенциал перескока атома (5) составляет

Δ F ∞ = 91.7 кДж/моль (7)

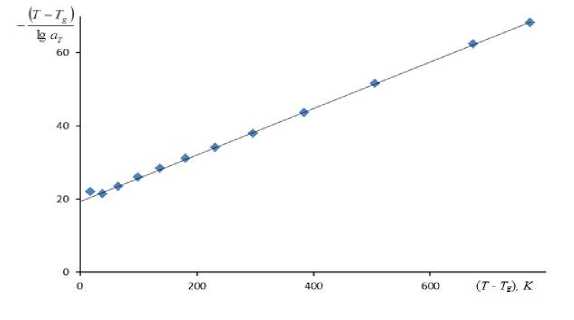
Рис. 2. Температурная зависимость вязкости листового силикатного стекла в координатах уравнения Вильямса-Ландела-Ферри: -( T - T g )/lg a T – ( T - T g ).

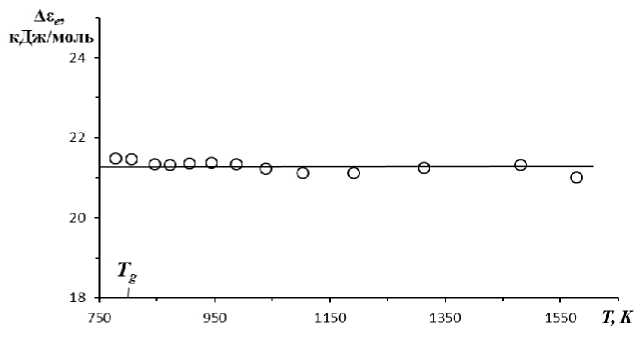
Рис. 3. Энергия делокализации атома в листовом силикатном стекле как функция температуры.

Подставив в формулу (3) Δ F η ( T ) и Δ F ∞ , соответственно, из соотношений (4) и (7), для данного стекла мы рассчитали энергию делокализации атома Δε e ( T ) в интервале температур 778–1578 K . Как видно из рис. 3, в области стеклования в достаточно широкой области температур энергия Δε e , необходимая для делокализации атома, оказывается практически постоянной и равной около Δε e = 21 кДж/моль.

В модели делокализованных атомов [8, 9] величина Δε e рассчитывается по формуле

∆ε е = RT g ln(1/f g )                   (8)

где f g = (∆V e /V) T=Tg – доля флуктуационного объема, замороженная при температуре стеклования T g . Флуктуационный объем аморфного вещества Δ V e возникает в результате тепловых смещений атомов из положения равновесия ( N e – число делокализованных атомов)

∆V e = N e ∆V e

Величина f g рассчитывается по данным о параметре уравнения ВЛФ C 1 и слабо зависит от природы стеклообразующих веществ [8]

f =   ≈ const ≈ 0.020 - 0.030

^{g C} 1

У стекол одного класса f g оказывается практически универсальной постоянной. Для щелочно-силикатных стекол можно принять f g ≈ 0.025 и T g ≈ 700 K , откуда по формуле (8) получаем оценку [8]

∆εе ≈ 21 кДж∙моль, что находится в согласии с приведенным выше расчетом Δεe для листового силикатного стекла по формуле (6) на основе данных о свободной энергии активации вязкого течения.

Таблица

Свободная энергия активации вязкого течения Δ F η ( T ) и энергия делокализации атома Δε e свинцовосиликатного стекла SiO 2 -PbO (49.54 мол.% PbO)

T , K	Ip g (η, )	g(η η 0 )	Δ F η ( T )	Δε e
			кДж/моль
1276,0	1,0	4,22	103,0	19,0
1111,8	2,0	5,22	111,0	18,7
1004,8	3,0	6,22	119,5	18,6
929,5	4,0	7,22	128,3	18,6
873,7	5,0	8,22	137,3	18,6
830,7	6,0	9,22	146,5	18,7
796,5	7,0	10,22	155,7	18,7
768,6	8,0	11,22	164,9	18,8
745,5	9,0	12,22	174,2	18,9
726,0	10,0	13,22	183,6	18,9
709,4	11,0	14,22	192,9	19,0
695,0	12,0	15,22	202,3	19,1
682,5	13,0	16,22	211,7	19,2

Примечание: использованы данные [14]. T g = 676 K , lg (η 0 , П) = -3.22, lg(η g , П) = 13.82, ΔF ∞ = 50.2 кДж/моль, C 1 = 36.9, C 2 = 163.4 K .

Аналогичные результаты нами получены для свинцовосиликатного стекла PbO-SiO 2 с содержанием PbO 49.54 мол.% [14]. Для него энергия делокализации атома остается постоянной и равной около Δε e ≈ 19 кДж/моль в широком интервале температур 682-1276 K (табл.). Характеристики данного стекла принимают следующие значения: T g = 676 K , lg (η g , П) = 13.82, Δ F ∞ = 50.2 кДж/моль, lg (η 0 , П) = –3.2, C 1 = 36.9, C 2 = 163.4 K .

Таким образом, энергия делокализации атома Δε e в силикатных стеклах практически не зависит от температуры в широком интервале в области стеклования. Полученные значения Δε e совпадают с результатом расчета по формуле (8), следующей из модели делокализованных атомов. Отсюда следует, что данная формула справедлива не только при температуре стеклования, она применима и при других температурах в области стеклования.