Свободные колебания многослойной некруговой цилиндрической оболочки, состоящей из вязкоупругих слоев

Постановка задачи. Рассматривается тонкая некруговая цилиндрическая оболочка постоянной длины L, состоящая из N изотропных вязкоупругих слоев, характеризующихся толщиной hk, модулем Юнга Ek, плотностью рk и коэффициентом Пуассона v k .

В качестве исходных могут быть использованы уравнения [1], основанные на гипотезах, сформулированных Э.И. Григолюком и Г.М. Куликовым [2], которые отличаются от классических уравнений полубезмоментной теории тонких оболочек наличием дополнительных слагаемых, учитывающих поперечные сдвиги слоев. Отбрасывание последних приводит к уравнениям для изотропной оболочки с физическими характеристиками, равными осредненным по толщине параметрам слоистой исходной оболочки и может давать существенные погрешности при расчетах:

Eh3     (, 9h2 л-L-v •      1    52F'

-р h П² W = 0,

—7---гл п 3 1--А А А х +--—

12(1 - V2) I b J           R2 (a2) da2

Eh d ² W .

А А F---— = 0,

R2(a 2) da 2

W

'1 - у А^X.

V b у

Здесь ^А — оператор Лапласа в криволинейной системе координат ^{а 1} , ^{а 2} , E, ^v , ^р - осредненные модуль Юнга, коэффициент Пуассона и плотность материала

* V*

соответственно, h - толщина оболочки, F , ^х - функции напряжений и

ТТЛ *

перемещений, W - нормальный прогиб, ^ - частота собственных колебаний, f ° ( ^а з ) , fk ^{( а} 3 ) , g ^{( а} 3 ) - функции, зависящие от поперечной координаты ^а 3 ,

,

G k ^,

параметры , , ,     ,                   ,       ,       ,            ,                     ,

~ q44, к, ck’ ck определяются по формулам [1,2]:

N

h = Z hk v = Z

N Eh k ~

А

- 1

k = 1

,

V

k = 1 1

2 νk

J

N ^vk^Ekhk~k

Z 1   2

^k = 1 ^{1 - v} k

E =1

2 ( v

h

,

V

ZE h ~' k=1 1 - v2 J

,

Yk =

E k h k c k

i - v2 V

NF hr

Ek hk ck

Z /   2

k=11 - vk J

A ^{- 1}

P =

,

N

Zpksk k=1

9 = 1

П 2

b = 12(1 - v 2 )q 44

,

П 1 n 3 ^,

Ehn 1

,

N - 1

П 1 = Z ^z k ⁿ 1 k Y k k = 1

2 3c 12,

N - 1

n2 = Z Zk П2k Yk - 3c 13 c 12,

k = 1

_N                                 1             " k

П3 = 4Zfe + 3Zk-1ZkYk -3c23 йк n1 k =) g (a3d“3, k=1                                                      "k-1

¹ i 3_        "k„                 ¹ 1 2

— h ⁿ 2 k = J ^a 3 g ^(a 3 ) d ^a 3 h^{h 12}           " k - 1                 ²

,

δ k

n3 k = J g (a3 )da3,

" k - 1             h^ k = h k ,

k ),

h^Z n    " n ( n =0,

c 13 =Z(Z k-1 + Z k )y k ,  c 12 =Z Z k П 3 k Y k , k=1

δ k

^X kn = J f k ^(a 3 ) f n ^(a 3 ) ^{d a} 3 , ⁽ n = °, ^k )

" k - 1

"k ,2/_.

^-5 ° ^)(S N ^-a 3 )

^ k    J f ° ^(a 3 ^^{d a} 3 -> f₀ (a₃) = —(a₃

"k-1                    ° a3

g(a 3) = J f°(a 3) da 3 °

fk(a3) = 4-(“3 -6k-1 )(8k -“3) hi

Gt = Et /[2(1 + vt)] Gk = Gkck

,,

q 44 =

N (

Z kk k=1V

2 ^ko. ^kk J

N

Z 4

k = 1

V

2 ^ 4 0 ^ kk J

G k

n ;² + z ^ k ° k = 1 ^ kk

G k

+^

~к = ¹ - c k ,   c k = / R k ( ^s e - i ^м s ^ds

⁰                     .                               (2)

В формулах (2) R k (s) – ядро релаксации напряжений материала для k -ого слоя, а Q = to + i а , где i = V - 1 , _ш — фундаментальная частота свободных колебаний, а – декремент колебаний.

Перепишем уравнения (1) в безразмерном виде:

где

£ 8

4/      3    \ 2         , дд²F „ (

£ (1 -£ тА)А X + k(ф) —у -Х(х-д s

£ ⁴ А ² F - к ( ф)— ( х-£ ² кАх ) = 0,

I                   д s ²

h ² n₃/[12 R ² ( 1 -v ² )]            -

³                  – малый параметр,

тонкостенность оболочки, ^А

–

координат ф а 2 /R безразмерные функции

и

оператор s = а 1 /R

,

напряжений

£2 кА/)= 0, характеризующий

Лапласа в криволинейной системе

F = F */(£ ⁴ EhR ² )    x = X* / R

, и перемещений   соответственно,

X = (pR2 )/(e£4 )q2   _ _ _    ~ __              а _ р Я \   -   - искомый частотный параметр, '^- переменная кривизна.

Здесь ^т , ^к - параметры, характеризующие поперечные сдвиги:

K л ² = ^{£ 2 к} K е/к ² = ^{£ 3} т к , т^     е ^ 0 _Гд _e K = ^п h Я ^bR )

,                               ,                    р ,д                                        .

Граничные условия имеют вид:

^F = ^{А F} = Х = ^аХ = ^а2Х = ⁰ , при s=0,l, l = LR .        (4)

Задача состоит в определении параметра ^ , для которого краевая задача (3), (4) имеет ненулевое решение.

Построение решения. Считаем, что локализация собственных колебаний происходит в окрестности некоторой “слабой” образующей ф ф0. Введем растяжение масштаба в окрестности этой образующей:

^ = ⁽Ф ^- Ф 0 ^)f

Согласно [3] решение будем искать в виде:

Х = Х m (ф) sin (mпs/l) F = Ф m (ф) sin (mns/l) m = 1,2,

где

^{ X m , ^Ф m ^} = :i ^{£ j /2} { X mj ⁽^ ) , f_mj И} exp | i f ^£ "^V2 q ^ ⁺ 1 a ^ 2

j = 0 ^L                     Ц ² JJ , Im a >  0 , (₆)

X = X ₀ +£X 1 +£ ² X ₂ + ...,

k (ф) = k (ф0 ) + £12 k '(ф0 )^ +1 £k Чф0 К +...

2                              (8)

В выражении (6) параметр q характеризует изменяемость решения в окружном направлении, а мнимая часть числа a, характеризующего скорость затухания амплитуды волн при удалении от линии ф ф0, должна быть положительной. Функции Хmj, fmj являются полиномами по £.

Подставляя (5) - (8) в (3), (4), получим последовательность уравнений:

j

Z A k X j — k = 0 ^k = 0                  , j 0,1,2,

X =(х_т ,-, f™ JT относительно вектор - функции    j ^х mj mj'

A

Матрица 0 имеет вид:

.

A о =

4          1

q — X 11 + Kq I k (^0 \лт( l )2 (1 + Kq2

- к (^o X^m/l )2 q4

а элементы матрицы ^ j при j ~ ¹ выражаются через производные по q и ^ 0 j A

- го порядка элементов матрицы 0 [3].

Из условия существования нетривиального решения системы (9) при находим формулу для частотного параметра нулевого приближения:

Xo (q ,Фо, m )= q4 /(1 + Kq2 )+(k 2 (^о )(nm/l)4)/ q4

j = о

,

.

^Aq, Фо m)

Минимизируя ^{04 о} , ' по q и ф ₀, из условий дк ₀ /а q дбк ₀ /дф ₀ = о ^,

0 находим число q ⁰ и “наиболее слабую” образующую ^{ф 0} .

Однородная задача в нулевом приближении имеет решение в виде:

X о (§) = Ро (§)Y 0

, где Р0 (^ - неизвестный полином, а Y = (1,   A0111A012)

.

При ^{j 1} система уравнений (9) является неоднородной. Но при (10), (11) она обращается в систему тождеств.

условиях

Условие совместности системы (9) при ^{j 2} приводит к соотношению для вычисления параметра а:

a = i

,

Pn fe)

а также к уравнению относительно P^{0 (} ^ ) :

d ² P 0

d^2

+ ia 2^^ + Ро + 2^ Ро +

~ d^    ^{0         0}

2 X 1

X

1Т^\ Р о = 0 ,  (12)

qq

^о       ^о где фф и qq - вторые производные частотного параметра нулевого приближения по соответствующим параметрам при ф ф0 и q q

.

При

х,=X”)=(12+n )VXqqx^ + тq6 /(i+Kq2)

решение в виде полинома Эрмита степени n:

уравнение

имеет

P0 [^) = Hn [^] 3 = Vc^ с = — ia

,,

Пример. В качестве примера рассмотрим тонкую некруговую трехслойную цилиндрическую оболочку эллиптического сечения с полуосями b =0,03 м, a =0,015 м ( a), постоянной длины L=0,45 м. В данном случае “наиболее слабыми” будут две образующие, проходящие через точки, где радиус кривизны поперечного сечения наименьший. Первый и третий слои имеют одинаковую толщину h1=h3 и 12

изготовлены из керамики с модулем Юнга E 1 =E 3 = ,5   0 Па, плотностью

= o, =2510 , ч                       =03          „

P1 p3         кг/м3 и числом Пуассона V1    3    , . Межслойный заполнитель изготовлен из фторопласта с E2=2,34'10 Па, р2 = 2150 кг/м3, V2 = 0,3 .

Будем считать здесь, что керамические слои подчиняются закону упругих деформаций, а межслойный заполнитель – закону вязкоупругих деформаций.

R, = R, = 0

Тогда ^{1    3}     , а ядро скорости релаксации напряжений для фторопласта [4]

R2 = 0,02366 e-3,33'10"4t t-0,95

Выполняя преобразование Лапласа функции R 2 , находим:

_    0,02366 Г(0,05)

^{С 2} = Z              ш-4 А^0,05

(iго — а + 3,33'10 )

, где Г(x) – Гамма- функция.

На рисунках 1,2 представлены графики параметров ω, α, как функций Mh    h, = h. = 0,0001

относительной толщины заполнителя 2 при 1    3    , м и различных значениях m. Цифрами 1, 2, 3 отмечены кривые, отвечающие волновым числам m=1, 2, 7 соответственно.

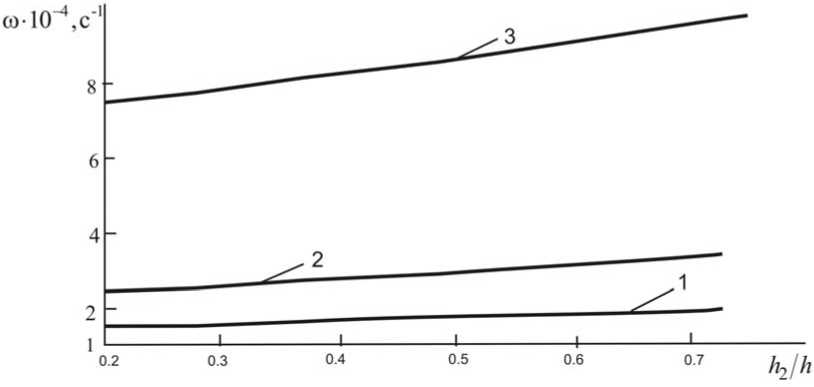
Рисунок 1 - Собственная частота колебаний

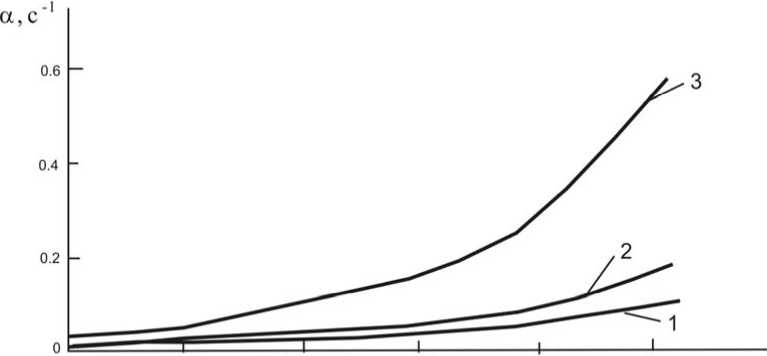
0.2             0.3              0.4               0.5              0.6               0.7

Рисунок 2 - Декремент колебаний h J h n c

В рассмотренном диапазоне изменения 0,2< 2   ≤ 0,73 собственная частота ω возрастает с ростом h2. Как и ожидалось, увеличение толщины заполнителя также приводит к росту декремента колебаний α.

Результаты работы могут быть использованы при проектировании тонкостенных элементов машин, а также габаритных тонкостенных инженерных сооружений в промышленном строительстве, летательных аппаратов и подводных тонкостенных объектов.