Свойства диффузионных импедансов Варбурга и Геришера в области низких частот

Одним из наиболее доступных методов исследования электрохимических и электрофизических процессов в ионопроводящих материалах является импеданс-спектроскопия (ИС) [1], что связано с относительно низкой стоимостью оборудования и достаточно высокой чувствительностью метода. Вместе с тем существует проблема интерпретации получаемых результатов. Это связано со сложностью процессов в материалах с ионной или смешанной электронно-ионной проводимостью. Такие объекты по своим свойствам имеют много общего с низкотемпературной плазмой. Для теоретического описания таких систем, строго говоря, необходимо привлекать магнитную гидродинамику [2].

Развитие теории ИС направлено на построение электрических эквивалентных схем (ЭС) образцов, что оказалось достаточно сложной задачей. Накопленный экспериментальный опыт показывает, что электрические свойства образцов часто не соответствуют резисторно-конденсаторным моделям. Для повышения точности часто требуется в ЭС вводить индуктивность или отрицательную емкость [3].

Таким образом, существуют процессы, приводящие к отставанию тока по фазе, природа которых неясна.

Вторая проблема связана с присутствием неустойчивых электрохимических процессов. Такие системы невозможно моделировать пассивными двухполюсниками. Однако при построении ЭС активные двухполюсники, имеющие внутренние источники энергии, в настоящее время не используют. Примером неустойчивости является коррозия электродов, что проявляется в регистрации отрицательной емкости при измерении электрических свойств методом ИС [4].

Третья проблема, которой и посвящена настоящая работа, связана с тем, что электрохимические ячейки являются системами с распределенными параметрами. При теоретическом описании таких объектов возникают функции от координат и времени, для нахождения которых требуется интегрировать дифференциальное уравнение в частных производных. Этот подход приводит к решениям в виде трансцендентных или иррациональных функций, что заставило расширить элементную базу электрохимической схемотехники особыми элементами, среди которых наиболее известен диффузионный импе- данс Варбурга (Warburg) [4]. Таким образом, построение ЭС, адекватно описывающее электрические свойства образца, требует серьезных экспериментальных и теоретических исследований.

Диффузионные импедансы Варбурга и Геришера

Как в радиотехнических системах, так и в электрохимии наиболее простые элементы с распределенными параметрами моделируют в виде полубесконечных лестничных схем (рис.1а).

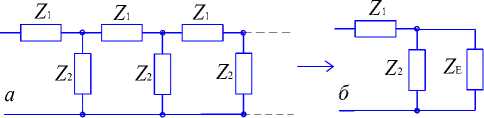
Рис. 1. Бесконечная лестничная схема ( а ) и её представление в виде двухполюсника конечных размеров ( б ).

Обычно полагают, что Z 1 и Z 2 – импедансы бесконечно малого отрезка объекта. Отсюда следует, что Z 1 – бесконечно малая величина, а Z 2 – бесконечно большая. Входной импеданс Z E можно легко определить, поскольку благодаря бесконечности цепи его величина не изменяется при удалении конечного числа звеньев. Это позволяет свести лестничную схему к простому двухполюснику (рис. 1б), из которого получаем в приближении Z 1 <<  Z E формулу для входног о имп еданса:

Z e = _V ZZ .. . (1)

В электрохимии известны два элемента, моделируемые лестничными схемами, – это импеданс Варбурга ( W ) [1, 4] и импеданс Геришера ( G ) [5]. На рис. 2 приведены схемы этих элементов.

lim a =—^= = k ; lim в = 0 ,             (7)

® ^ 0     Tp       to ^ 0

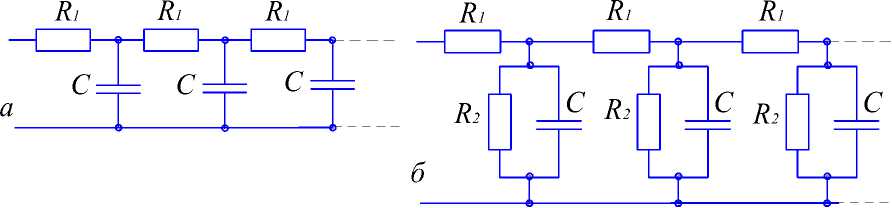
Рис. 2. Эквивалентные схемы импеданса Варбурга ( а ) и Геришера ( б ).

Импеданс Варбурга Zw имеет Z, = R1 - актив ное сопротивление и Z2 = —1--импеданс емкости jωC

С ( j' - мнимая единица; ю - частота). После подстановки в (1) получаем известное выражение для импеданса Варбурга [1]:

Z

w

R 1 jωC

Из соотношения (2) следует основное свойство W . Независимо от частоты ток опережает напряжение по фазе на 45 ° . Однако такое поведение в экспериментах никогда не наблюдалось [5]. Импеданс

Геришера (рис. 2б) в некоторых случаях точнее описывал экспериментальные результаты, что привело к его использованию в эквивалентных схемах в качест- ве отдельного электрохимического элемента [5]. С помощью соотношения (1) из схемы на рис. 2б находим выражение для импеданса Геришера:

^Z G =

R 1 R 2

j®R ₂ C + 1

Соотношения (2) и (3) можно записать в виде одной формулы, если использовать переменную Лапласа p , которую также называют комплексной частотой [4]:

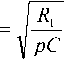
где p = J® для W и p = J® +1 для G; T = R2C - постоянная времени.

Поскольку в выражении для импеданса присутствует p , то для расчета электрических характеристик потребуется ряд формул. Преобразуем p к алгебраическому виду:

pP = ^ J® + T ⁼ a + je ’        (5)

где α и β – соответственно, реальная и мнимая части, которые можно определить по следующим формулам:

a = -1= W ® ² T ² + 1 + 1 , в =         ®² T ² + 1 - 1 . (6)

2 T                    2 T

Эти величины на низких частотах равны:

где k – параметр, пропорциональный проводимости на постоянном токе.

Низкочастотную асимптоту для функции β можно получить из (6):

T 1 в = ®   = ®  .

2     2 k

Соотношения (6) – (8) потребуются для дальнейших вычислений.

Кратко рассмотрим физические процессы, которые моделирует импеданс Варбурга [6, 7]. Под действием подаваемого на электрохимическую ячейку синусоидального напряжения при одной полярности происходит растворение электрода с об- разованием избыточных ионов, а при другой полярности – восстановление ионов и их осаждение на электрод. В рассматриваемой модели полагают, что макроскопическое поле в электролите ничтожно мало благодаря его высокой проводимости. Вслед- ствие этого перемещение ионов по электролиту возможно только за счет диффузии. Для получения зависимости диффузионного импеданса от частоты необходимо решить уравнение диффузии (второй закон Фика):

д c _ д ² c

-D    П , д t      дx2

где с – концентрация ионов; D – коэффициент диффузии; t – время; x – координата в направлении диффузионного потока.

По условию задачи входное напряжение меняет потенциал электрода по гармоническому закону: U = U ₀ e^jmt ( U 0 - амплитуда потенциала). Кроме этого предполагается, что избыточные ионы образуются только на электроде ( x =0 ), а их концентрация с пропорциональна подаваемому напряжению. Отсюда получаем первое граничное условие: с (0) = с ₀ e^jmt , где с _о - константа. В рассматриваемой модели ионы не способны достигать противоположного электрода ввиду значительной толщины ячейки. Таким образом, второе граничное условие равно: с ( да ) = 0 .

Установившееся решение уравнения (9) имеет вид произведения функции времени на функцию координаты:

c ( x , t ) = c ( x ) exp( jtot ) , (10)

где c(x ) - комплексная амплитуда колебаний концентрации частиц. После подстановки (10) в (9) и сокращения временной функции, получим линейное дифференциальное уравнение второго порядка одной переменной x :

.               d2 c (x)....

jtoc (x) = D ——2— .

dx ²

Решение уравнения (11) с учетом граничных условий позволяет определить адмиттанс ячейки [1, 6]:

Yw = Bj = B,[P ,(12)

где

9 9_ n 2 F 2 cVD

RT

– константа для электрохимиче- ской ячейки с жидким электролитом, с – средняя концентрация ионов в растворе, n – валентность ионов, F - число Фарадея, T- температура в К, R – газовая постоянная.

Распределение заряда по конденсаторам на рис. 2а соответствует распределению избыточных ионов по ячейке. Резисторы R2, шунтирующие емкости в модели Геришера (рис. 2б), приводят к разряду конденсаторов. Поэтому существует предположение о том, что G моделирует диффузионный процесс нестабильных частиц [5]. Распад частицы означает выбывание её из диффузионного процесса за счет, например, потери подвижности. При этом непонятно, куда исчезает заряд. Для его нейтрализации необходимо вводить в модель носители заряда противоположного знака, что также по- влияло бы на импеданс образца. Однако этот фактор в рассматриваемой модели не учтен.

В теории обоих диффузионных импедансов игнорируется накопление объемных зарядов. В импеданс спектроскопии на образцы подают потенциал с частотой от 0,001 Гц до 1 МГц. На сверхнизких частотах полубесконечная ячейка способна аккуму- лировать значительные заряды даже при минимальных токах. При этом поле объемных зарядов должно оказывать тормозящее действие на диффузионный поток. Учесть влияние объемных заря- дов можно за счет введения дополнительного слагаемого в (9):

д с _ д2 сс

D ■)

д t дx2

где τ – константа с размерностью времени.

Решение уравнения (13) также следует искать в виде (10). После подстановки (10) в (13) получаем следующее уравнение:

.           _n d ² c ( x ) c ( x )            ....

jtoc ( x ) = D Д - -^.       (14)

dx ² т

Уравнения (11) и (14) по своей структуре одинаковы. Если использовать переменную Лапласа p , то оба уравнения приобретают следующий вид:

_n d ² c: ( x )

pc ( x ) = D —-₄— ,           ⁽¹⁵⁾

dx ²

где p = jto для классического импеданса Варбурга и p = jto +1 для импеданса Варбурга, в который τ введена поправка на объемные заряды.

Значения переменной Лапласа в соотношениях (4) и (15) одинаковы. Следовательно, учет объемных зарядов преобразует импеданс Варбурга в импеданс Геришера. Таким образом, G моделирует диффузионный процесс, сдерживаемый объемными зарядами. В этом подходе отсутствуют сформулированное выше противоречие модели нестабильных частиц.

Адмиттанс Геришера получаем из (12) после

1 замены p = jto + — :

τ

Y g = B 71 + jtoT .            (16)

τ

Из (16) с помощью формул (6) получим измеряемые величины: проводимость cG = ReYG и ем кость Cr = —ImYr:

GG ω oG = -B= VV to 2т2 +1 +1, CG = -B- V7 to 2т2 +1 -1 .

V2 т                    V2 rto

Проводимость и емкость W находим из (17) при т ^ да :

^ W = B_A^to ,      C w = B_A 1- .         (18)

V 2                  v 2 to

При перемножении обоих выражений (17) частота сокращается, что позволяет получить зави- симость емкости от проводимости (Сс-диаграмму [8]), которая выражается гиперболой:

R ²

C g = — .             (19)

^{2 c} g

ет из схемы на рис. 2а. Если число звеньев равно n , то R ₀ = nR 1 .

Поскольку в (19) т не входит, то и для W Сс- диаграмма будет также гиперболой, что было ранее показано в работе [7]. Вместе с тем между эти-

Во втором случае полагают, что ионы не способны к адсорбции и восстановлению на противо-электроде. Соответствующая эквивалентная схема (рис.2а) не должна иметь какую-либо нагрузку на выходе. Для этого случая входной адмиттанс равен [4]:

ми двумя кривыми имеется существенное различие, которое заключается в положении на С с -плоскости начальной точки диаграммы (для нулевой частоты). Координаты этой точки ( C G , с G ) можно определить из (17) с помощью соотношений (7). Для импеданса Геришера положение начальной

YbW (p) =   B^   , ch(R 0 BVp )

точки

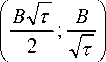
а для импеданса Варбурга –

где ch - гиперболический косинус.

Электрохимический процесс, как правило, идет по первому способу. В работе [9] был проведен подробный анализ соотношения (21). Показано, что при больших значениях p : Y_BW = Bjj . Это оз-

( да ; 0 ). Следовательно, при уменьшении т С с -диа-грамма с низкочастотной стороны начинает укорачиваться.

Из соотношения (17) вытекает алгебраический критерий, позволяющий отличить импеданс Варбурга от импеданса Геришера. Существует следующая независящая от частоты величина:

(Re Y g )² - (Im Y g )² = — . (20) τ

Таким образом, если разность квадратов реальной и мнимой частей адмиттанса не зависит от частоты и больше нуля, то это указывает на диффузионный процесс Геришера. Если указанная разность равна нулю, то имеет место диффузия по Варбургу.

начает, что на высоких частотах конечный диффузионный импеданс совпадает с импедансом Варбурга.

В литературе конечный импеданс Геришера ранее не рассматривался. Вместе с тем соотношение (21) можно обобщить и на этот элемент, который можно было бы обозначить через BG (Bounded Gerischer). Если выразить гиперболический тангенс через экспоненты, то соотношение (21) приобретает следующий вид:

_Y       ^B4p ^[exP⁽² R 0 ^B^ ) + ^1]      ,007

YBG ⁽ p )                    I—          .       ( ²³⁾

exp(2 R 0 Bjp ) - 1

Конечные диффузионные импедансы Варбурга и Геришера

Подставим (5) в (22), что даст следующую формулу:

αν jβν ybg = B(a + )P)-v^ ,       (24)

e e — 1

где v = 2 R ₀ B - константа. Далее в (24) убираем

Рассмотренные выше импедансы W и G относятся к полубесконечным электрохимическим ячейкам. Это означает, что образовавшиеся ионы не способны в процессе диффузии переместиться через всю ячейку. Однако при низких частотах влияние противоположного электрода необходимо учитывать. Для этого случая в теорию электрохимического импеданса было введено понятие конечного диффузионного импеданса BW (Bounded Warburg) [1, 4]. Этот элемент моделируют лестничной схемой (рис. 2а), состоящей из конечного числа звеньев. Таким образом, необходимо ввести до-

мнимую единицу из знаменателя. Это достигается

умножением числителя и знаменателя на комплексно сопряженный знаменатель. В результате

получаем следующее выражение:

² av    av tfv    ^— j ?,^]

Y_bg = B (a + jp )         (—.

^BG                - ^{2 v} — - ^av ( -^jPv + - ^— j ^ev ) + 1

Теперь необходимо воспользоваться известными из теории комплексных чисел формулами:

1                                    1

cos ф = —( e^{J< p} + e ^{) ф} ); sin ф = —( e^{J< p} — e ^{) ф} ).

полнительное граничное условие, связанное с противоположным электродом ячейки. Известны два различных случая [4]. Во-первых, полагают, что выход лестничной схемы соединен с резистором. Это означает, что при низких частотах большая

Соотношение для адмиттанса (25) приобретает следующий вид:

Y = B (a + )в )( e^{2 v} ~ 2 je ^av sin( pv ) — 1)

^BG          e^{2 v} - 2 e ^av cos( pv ) + 1

.

часть ионов, достигших противоположного электрода, осаждается на нем с передачей заряда во внешнюю цепь. Адмиттанс BW для этого случая равен [1, 4]:

Из (26) можно получить измеряемые величины (проводимость σ BG и емкость С BG для параллельной схемы замещения). Для этого в числителе (26) необходимо перемножить скобки и разделить

мнимую и вещественную части:

Y „ ( Р ) = -B V , ^{th( R} 0 Bjp )

σBG

= Re Y BG

B - ( з^{2 av} + 2 pe ^av sin( pv ) — a e ^{2 v} _ 2 - ^av cos( py ) + 1

где B - константа, входящая в выражение (12); th -гиперболический тангенс; R ₀ - активное сопротивление BW при нулевой частоте. Толщина электрохимической ячейки пропорциональна R o , что следу-

r

C BG

Im Y BG

ω

B в-^{2 av} — 2ae ^av sin( pv ) — p _ю - ^{2 v} _ 2 - ^av cos( pv ) + 1

При использовании функций гиперболического синуса ( sh ) и гиперболического косинуса ( ch ) соотношениям (27) и (28) можно придать более ком-

пактный вид:
α sh( αν ) + β sin( βν ) σ = B                  , ch( αν ) - cos( βν )	(29)
C = B β sh( αν ) - α sin( βν ) BG ω ch( αν ) - cos( βν ) .	(30)

Соотношения (27) – (30) позволяют построить любые частотные зависимости как для конечного импеданса Геришера ( BG ), так и для конечного импеданса Варбурга ( BW ).

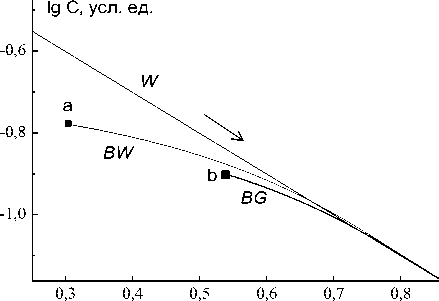
На рис. 3 приведены в логарифмическом масштабе Cσ -диаграммы диффузионных импедансов W , BW и BG . Кривые построены с использованием соотношений (6), (19), (29) и (30), в которых приняты значения: B = ν = 1 усл. ед. и τ = 0,1 усл. ед.

lg σ , усл. ед.

Рис.3. С σ -диаграмм W , BW и BG . Точками a и b обозначены низкочастотные пределы. Стрелка указывает направление роста частоты.

Из рис. 3 следует, что основные отличия между BW и BG наблюдаются на низких частотах. При этом положение точки b зависит от постоянной k. С помощью соотношений (7), (8), (27) и (28) можно получить зависимость координат начальной точки Сσ-диаграммы от k:

exp( kν ) + 1

lim σ_BG = Bk           ,

^{ω → 0}         exp( kν ) - 1

lim С_BG ω → 0

B exp(2 kν ) - 2 kν exp kν - 1 2 k       [exp( kν ) - 1]²

Координаты точки a (рис. 3) находим с помо- щью следующих пределов:

lim σ = ¹ , lim С (0) = ^{B R 0} .       (33)

BG       ,            BG k→0       R0       k→0 BG        3

Полученные значения (33) совпадают с данными из работы [9].

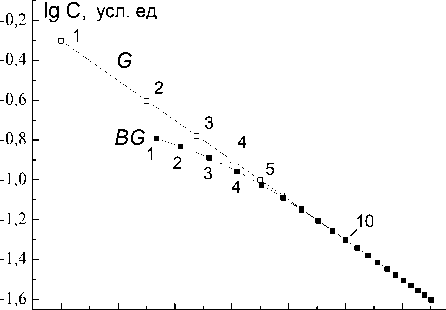
На рис.4 приведены положения на С σ -плоскости начальных точек С σ -диаграмм обоих им-педансов Геришера. Из рис. 4 следует, что при увеличении параметра k различие между G и BG уменьшается. При k > 5 оба импеданса совпадают. Наиболее сильные различия между BW и BG проявляются на фазочастотных характеристиках (рис. 5). Возникновение небольшого экстремума на фазочастотной характеристике BW (рис. 5) объясняет-

0,0     0,2     0,4     0,6     0,8     1,0     1,2

lg σ , усл. ед

Рис. 4. Положение начальной (для нулевой частоты) точки на С σ –плоскости в зависимости от константы k : G – импеданс Геришера; BG – конечный импеданс Геришера. Цифры, расположенные около точек, равны значениям k .

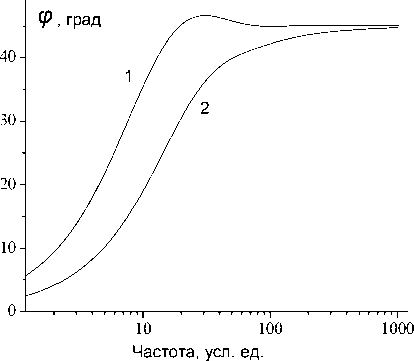
Рис. 5. Зависимости сдвига фазы от частоты для конечных импедансов Варбурга (1) и Геришера (2). Графики построены для B = ν = 1 усл. ед и τ = 0,1 усл. ед.

ся интерференцией падающей волны и волны, отраженной от противоположного электрода. Этот экстремум не наблюдается для BG , так как объемные заряды в значительной степени гасят волну.

Заключение

Проведенный анализ показал, что различия между четырьмя диффузионными импедансами проявляются только на низких частотах. При повышении частоты все модели сводятся к импедансу Варбурга. По данным импеданс-спектроскопии достаточно легко установить, какая из четырех моделей наилучшим образом описывает экспериментальные результаты. Различить диффузию по Ге-ришеру и Варбургу следует с помощью критерия (20), который позволяет также определить постоянную времени τ (для модели G ). Влияние противо-электрода на диффузионный процесс можно установить по C σ -диаграмме, построенной в логарифмическом масштабе. Диффузия по Варбургу от диффузии по Геришеру отличается также по фазочастотной характеристике в области низких частот.