Свойства фрактального трафика при прохождении системы массового обслуживания с очередью

Введение. В последние годы для математического моделирования трафика пакетных сетей передачи данных все чаще используются фрактальные стохастические процессы [1–4]. Фрактальные потоки, являясь развитием классических моделей теории телетрафика, учитывают такие свойства нагрузки, выявленные в современных высокоскоростных сетях, как склонность к всплескам, наличие внутренней корреляции и последействия, медленное сглаживание характеристик при рассмотрении в укрупненном временном масштабе.

В настоящей статье рассматриваются статистические характеристики фрактального потока после обработки в системе массового обслуживания с очередью, т. е. в общем случае, на произвольном участке сети массового обслуживания. Показано, что после прохождения системы с очередью фрактальные свойства сохраняются, причем степень выраженности этих свойств зависит от степени загрузки системы.

Основные понятия фрактальных моделей трафика. Понятие фрактальных (fractal), или самоподобных (self-similar), случайных процессов опирается на геометрическое понятие фрактала – объекта, в котором часть некоторым образом подобна целому. Аналогичным образом, случайный процесс X ( t ) является самоподобным с параметром Херста H , если X ( t ) и a^–HX ( at ) имеют идентичные конечномерные распределения вероятностей для всех a >  0, т. е. процесс существенно не меняет вида при масштабировании по шкале времени – часть траектории процесса, как во фрактале, подобна целому, но не геометрически, а статистически. Параметр Херста Н может принимать значения из интервала [0,5; 1), значение 0,5 означает полное отсутствие фрактальных свойств, рост Н в сторону 1 – усиление выраженности самоподобного характера. Исчерпывающий обзор подходов к определению фрактальных моделей приведен в работе [4].

В зависимости от особенностей предметной области и целей моделирования, для описания трафика используются различные классы случайных процессов, в том или ином отношении обладающие фрактальными свойствами. Так, в качестве модели трафика магистральных каналов, агрегирующих потоки от значительного числа источников, могут применяться модели фрактального броуновского движения [5] или α-устойчивые процессы [6], общей характеристикой которых является определение процесса как последовательности отсчетов {xi }, соответствующих количеству пакетов или байтов в потоке на последовательных единичных интервалах времени. Для описания поведения сети на уровне пропуска отдельных пакетов разработан класс точечных фрактальных процессов, траектория которых представляет собой последовательность {ti } моментов поступления очередного пакета. Хорошо проработан аппарат фрактальных On–Off процессов, рассматриваемых как чередование периодов активности и пауз, длительности которых обладают самоподобными свойствами, либо как суперпозиция нескольких таких последовательностей. Также предложены модели, опирающиеся не на кон- кретные модели потоков, а на их универсальные статистические характеристики [7].

Модель трафика на основе фрактального дробового процесса (FSNDP). В результате исследования реальных срезов Ethernet-трафика в действующих информационных системах автоматизации бизнес-процессов оператора связи авторами ранее было показано [8], что в качестве адекватной модели потока пакетов в распределенной системе обработки данных с вынесенными рабочими местами может использоваться один из фрактальных точечных процессов, а именно, фрактальный дробовой процесс, также называемый процессом FSNDP (Fractal Shot Noise Driven Poisson) [6; 7]. Для этого процесса существуют подходы к статистической оценке параметров по полученным дампам реального трафика, он также поддается корректной и вычислительно умеренно трудоемкой генерации по заданным параметрам [4–15].

Переменная во времени интенсивность процесса FSNDP задается непрерывным случайным процессом – фрактальным дробовым шумом, который получается путем фильтрации классического пуассоновского процесса.

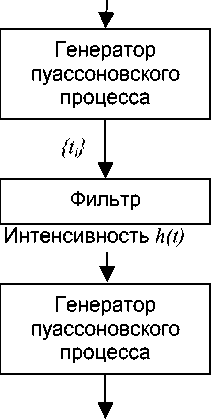
Процесс FSNDP полностью определяется набором из пяти параметров (ц, в , K, A, B), имеющих сле- дующий смысл.

Первичный пуассоновский поток { t_i } с постоянной интенсивностью μ служит входом для линейного фильтра с импульсной функцией

Kt ^-р , t е ( A , B ) 0, 1£ ( A , B ),

где в определяется степенью самоподобия процесса;

А , В – неотрицательные ограничивающие параметры; K – положительная константа, определяющая амплитуду результирующего процесса. Фильтр порождает фрактальный дробовой шум

X

I ⁽ t ) = z h ⁽ t ^- t i ) i =-x

рассматриваемый как переменная интенсивность для второго пуассоновского точечного процесса, выходом которого является поток FSNDP (рис. 1).

Параметр в определяется степенью самоподобия процесса и связан с параметром Херста Н :

H = 3/2 -р . (3)

Процесс обладает устойчиво самоподобными свойствами при условии А << B и А , достаточно близком к нулю . В практических моделях обычно принимается, что А = 0 или А = 10 ^{- 7}.

Поток на выходе системы FSNDP/D/1. Результаты имитационного моделирования показывают, что последовательность событий, соответствующая моментам завершения обработки заявок в однолинейной системе массового обслуживания (СМО) с очередью и потоком FSNDP на входе, т. е. поток на выходе СМО после обработки, сохраняет фрактальные свойства.

На рис. 2 приведена зависимость средней длины очереди q (ρ) в зависимости от загрузки системы ρ для искусственно сгенерированных срезов потока FSNDP, параметры которых отражены в таблице. Параметры срезов потока выбраны, исходя из роста параметра Херста Н: 0,55 соответствует незначительному проявлению фрактальных свойств, при Н = 0,6 и далее 0,7 фрактальные свойства уже более сущест- венно выражены. Соотношение (3) позволяет предусмотреть значение Н при генерировании среза потока, задавая показатель β. Однако так как данный показатель влияет также на итоговую интенсивность λ (соотношения для статистических характеристик фрактального дробового процесса приведены в [7]), для получения сопоставимых по интенсивности срезов помимо β варьировался коэффициент K.

Интенсивность µ

FSNDP

Рис. 1. Составляющие процесса FSNDP

A

t

t

A mu in mi i.

t

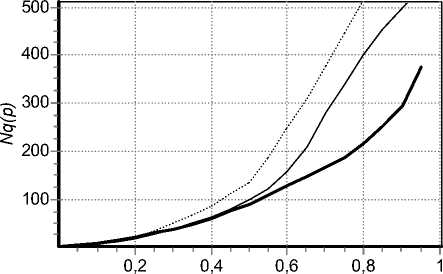
Рис. 2. Оценка длины очереди в СМО FSNDP/D/1 в зависимости от загрузки системы при возрастании степени самоподобия: H = 0,55, 0,6 и 0,7

Параметры срезов потока

	1	2	3
Длительность, с	1000	1000	1000
μ	0,025	0,025	0,025
K	10	20	40
β	0,95	0,9	0,8
A	0	0	0
B	100	100	100
Параметр Херста Н	0,55	0,6	0,7
Средний объем пакета, байт	100	100	100

Ранее было установлено [8], что реальному сетевому трафику в моделях FSNDP наиболее соответствует модель с постоянным временем обслуживания (что в терминах предметной области означает постоянный объем пакета). По аналогии с классической теорией массового обслуживания, основанной на марковских потоках, исследуемую СМО можно обозначить как FSNDP/D/1.

Оценка параметра Херста в потоке на выходе системы FSNDP/D/1 (рис. 3) показывает, что степень самоподобия зависит как от степени самоподобия в исходном потоке, так и от загрузки системы. На основании проведенных имитационных экспериментов можно сформулировать следующие выводы.

• 1.    Значение параметра Херста Н возрастает с ростом загрузки СМО. Н существенно растет при ρ до 0,4–0,5, далее рост замедляется, для высоконагру-женных систем Н превышает 0,9, что означает поток с крайне высокой степенью фрактальности, и дальнейшее увеличение ρ на фрактальность выходного потока существенного влияния не оказывает. Такое поведение характерно для исходных потоков как с маловыраженным самоподобием, так и с ярко выраженным.

• 2.    Для слабонагруженных систем значение параметра Херста в выходном потоке несколько выше входного, но сопоставимо со входным. Это может использоваться как приближение при имитационном моделировании и при численных расчетах. Статистические характеристики входного и выходного потоков слабонагруженной СМО FSNDP/D/1 в части фрактальных характеристик могут условно считаться одинаковыми.

Для систем с высокой загрузкой влияние степени самоподобия входного потока нивелируется, значения на выходе оказываются одинаковыми, приближенны- ми к 1, даже для входных потоков с крайне слабо выраженными фрактальными свойствами (H < 0,6). Это, однако, имеет малое практическое значение, так как для фрактального трафика очередь в СМО растет крайне быстро с ростом ρ за счет высокой пачечности и сильной корреляционной структуры; область ρ > 0,5–0,6 на практике означает систему, режим которой близок к выходу за пределы стационарного.

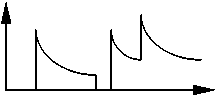
На прикладном уровне явление роста самоподобных свойств с ростом загрузки СМО может быть объяснено «эффектом полки», когда в пиковых интервалах за счет ограниченной пропускной способности независимо от поступления исходной нагрузки на выходе формируется постоянное или близкое к постоянному значение, соответствующее ограничению полосы (на рис. 4 профиль трафика для искусственно сгенерированного среза 3 с Н = 0,7). В предельном случае, для высоконагруженных систем с ρ, стремящимся к 1, можно получить постоянный профиль трафика без случайных флуктуаций, «срезанный» по ширине полосы и полностью заполняющий канал. При этом в теории фрактальных процессов известно [4], что детерминированный процесс без случайной компоненты является абсолютно самоподобным с параметром Н = 1. Рост Н в сторону 1 при увеличении выраженных постоянных фрагментов выглядит объяснимым.

Заключение. Полученные результаты позволяют говорить о том, что поток на выходе СМО с фрактальным поступлением не только сохраняет общие фрактальные свойства, но и демонстрирует устойчивые зависимости как от параметров входного потока, так и от параметров СМО. В настоящее время ведется работа над исследованием характера этих зависимостей с целью получения соотношений, которые позволили бы численно оценить характеристики потоков.

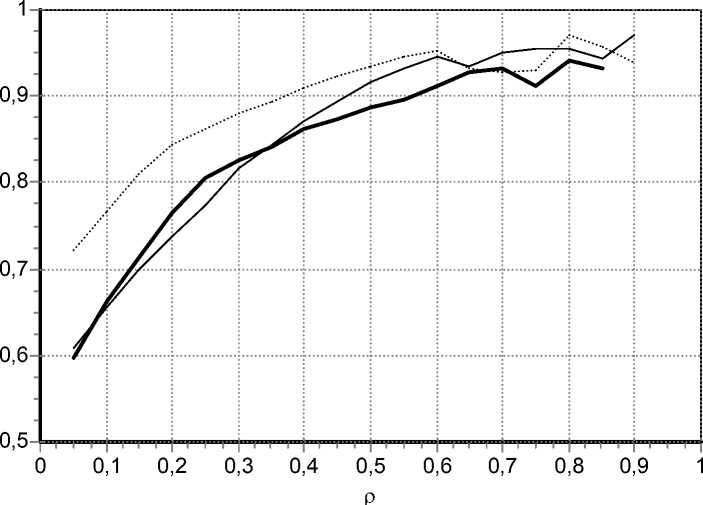
Рис. 3. Зависимость Н от загрузки системы в выходном потоке для моделей таблицы

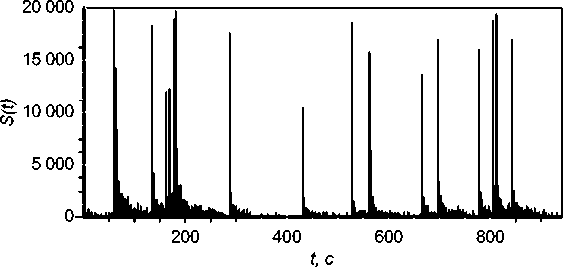
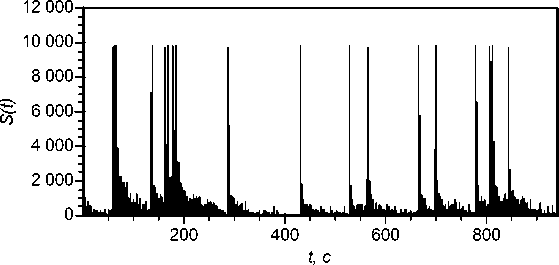
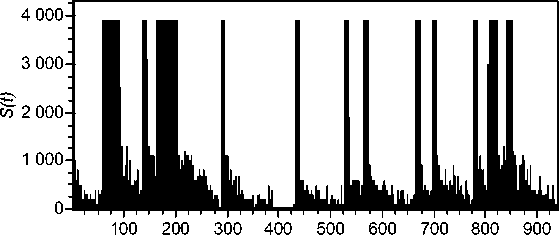
t, c

Рис. 4. Профиль трафика модели: входной, выходной с загрузкой 0,05 и 0,25

Также выявленный эффект, следствием которого является общность качественных характеристик фрактальных потоков до и после прохождения системы массового обслуживания с очередью, открывает широкое поле для исследований в области сетей массового обслуживания, в частности, на основе тензорных методов.

Актуальность темы статьи подтверждается исследованиями в работах [16; 17].