Свойства медианы с учетом дрейфа одного из группы измерителей (на примере равномерного распределения)

Применение медианы необходимо повсеместно, в частности и при разработке приборов радиационного контроля. Современным тенденциям развития интеллектуальных систем такого назначения характерно размещение измерительных приборов на борту беспилотных летательных аппаратов (БПЛА) [1]. Имеется возможность выбирать различные типы БПЛА, не ограничиваясь легким классом с грузоподъемностью до 3 кг. Например, БПЛА "Чирок" [2] поднимает 275 кг полезной нагрузки. Это означает, что на БПЛА может быть установлен и измеритель мощности дозы [3–5], имеющий вес 17 кг, разработанный для наземных транспортных средств. А также можно не ограничиваться 24 счетчиками Гейгера—Мюллера (в существующей разработанной модификации); открыт путь к разработке более сложных вариантов.

Наращивание количества чувствительных элементов для повышения точности измерения мощности дозы (и угла направления на источник излучения) производится принципиально в связи со случайной природой радиоактивного излучения. Такая необходимость обусловлена и ограниченностью интервала времени измерения (движущегося окна) в условиях движения БПЛА или иного транспортного средства с заданной скоростью.

Параметры различных производимых счетчиков регистрации излучения представлены в [6]. При этом в графе "Чувствительность" указано, например, 60–75 имп/мкР для счетчика Гамма-7;

285–385 имп/мкР для счетчика Гамма-8; 31– 39 имп/мкР для счетчика Гамма-10. Как видно, каждая модель допускает изначальный разброс около 25 %. В связи с этим требуется настройка параметров программного обеспечения (коэффициентов чувствительности) в устройствах радиационного контроля прежде всего на этапе изготовления, а также и периодически на этапе эксплуатации.

Актуальность статьи обусловлена возрастанием требований по точности и надежности измерений в экстремальных условиях эксплуатации, когда замена неисправных чувствительных элементов (датчиков) затруднительна или невозможна и возникает необходимость защищаться от их неисправностей и дрейфов чувствительности.

Дрейфу подвержены все чувствительные элементы, но в промежутке времени между сеансами пересчета коэффициентов чувствительности чрезмерный дрейф наиболее вероятен только у одного чувствительного элемента (измерителя). Поэтому в данной статье поставлена цель получить формулы, позволяющие анализировать (оценивать) влияние дрейфа одного измерителя на математическое ожидание и дисперсию медианы.

Решение поставленной задачи зависит от вида функции плотности вероятности распределения значений, получаемых от датчиков. В рамках данной статьи выбрано равномерное (прямоугольное) распределение, являющееся наиболее простым, допускающим получение удобных аналитических формул.

ИСХОДНЫЕ УСЛОВИЯ

Пусть задана функция p ( a , x ) — плотность вероятности распределения измеряемой величины x в области значений, ширина которой характеризуется параметром a .

Запишем и интегральную функцию вероятности распределения:

X

P ( a , X ) = j p ( a , x ) d x .

-to

Пусть L — величина дрейфа одного измерителя в сторону занижения. Это значит, что функция плотности вероятности приобретает вид p ( a , x + L ) .

Предположим, что применяется исходное нечетное количество одинаковых датчиков (измерителей) N , которое связано с целочисленной половиной n по формуле N = 2 n + 1.

Например, ИМД-24 [3, 4, 5] содержит 24 чувствительных элемента. При этом в [5] cообщается, что в случае наличия точечного источника радиации 17 чувствительных элементов полностью принимают его излучение, а 5 чувствительных элементов, оставаясь в тени цилиндра, принимают только фон. Понятно, что за счет анализа таких данных можно вычислить угол направления на источник. Но главным требованием является надежное вычисление мощности дозы, поэтому уместно игнорировать 7 наименьших значений, независимо от причины их вытеснения в край списка сортированных значений, а для вычисления мощности дозы рассматривать оставшиеся 17 значений.

Будем считать, что размер серединного интервала равен единице. В качестве итогового измеренного значения будем брать значение, оказавшееся в середине сортированного списка.

ИСХОДНОЕ СОСТОЯНИЕ ДАТЧИКОВ (БЕЗ ДРЕЙФА)

В качестве серединного в сортированном списке может оказаться любой из N датчиков, а в каждой из двух групп по n датчиков со значениями x <  X или x >  X все варианты последовательности их размещения в сортированном списке равнозначны. Имеем "перестановки с повторениями" [7, с. 48], количество которых определяется мультиномиальным коэффициентом

, _x (2 n + 1)!

W ⁽ n ^{) =} ^T^

Вероятность получения значения медианы в интервале от X до X + dX:

Q (a, X, n) dX = W (n) P (a, X) n (1 - P (a, X)) n x x p (a, X) dX. (1)

В [8, с. 96] коэффициент W ( n ) представлен через биномиальный коэффициент, а в [9, с. 17, 18] — с помощью бета-функции.

Далее, чтобы брать интегралы, будем пользоваться свойством вероятности полного набора событий to

J Q ( a , X , n ) d X = 1.          (2)

-to

Математическое ожидание медианы (момент первого порядка) имеет вид to

M ( 1, a , n ) = J Q ( a , X , n ) X d X .      (3)

-to

Момент второго порядка медианы (для вычисления среднеквадратического отклонения):

to

M ( 2, a , n ) = J Q ( a , X , n ) X ² d X .     (4)

-to

Рассмотрим вариант равномерного распределения на заданном интервале. При этом без ограничения общности для удобства вычислений можно считать, что среднее значение равно нулю. Интервал случайного разброса значений, получаемых от каждого датчика, обозначим [-a,a]. Плотность вероятности распределения имеет вид:

p ( a , x ) = У ( 2 a ) при - a <  x <  a ;

p ( a , x ) = 0      при x <- a или x >  a .

Интегралы пропорциональны интервалам ин- тегрирования:

P ( a , X ) = ( a + X )/( 2 a ) ;             (6)

1 - P ( a , X ) = ( a - X )/( 2 a ) .          (7)

Подставляя (6) и (7) в (1), затем в (2), с учетом симметричности (четности) подынтегрального выражения получаем a

n ) J ( a ² - x ² ) d x 0

( 2 a ) ² n ^{+ 1} = 1.     (8)

В дальнейшем этот интеграл потребуется также и в виде a

J ( a ² - x ² ) n d x = ( 2 a ) ² n ⁺ 1 /( 2W ( n ) ) .      (9)

Считаем, что все датчики одинаковы, поэтому для вычисления математического ожидания интегрирование нечетной функции происходит очевидным образом:

M ( 1, a , n ) = 0.

ДИСПЕРСИЯ МЕДИАНЫ ПРИ ОДИНАКОВЫХ ДАТЧИКАХ

Симметричность (четность) подынтегрального выражения позволяет ограничиваться рассмотрением положительной области:

a

, a , n ) = 2W ( n ) J x ² ( a ² - x ² ) d x

( 2 a ) ’ n ^{+ 1} .    (10)

Смещая индекс n , запишем (9) в виде

a

J ( a ² - x ² ) n ^{+ 1} d x = ( 2 a ) ’ n ⁺ 3 /(2 W ( n + 1 )).         (11)

Этот интеграл можно записать и как два интеграла:

Г / 7       7 \ n +1

I I a - x ) d x = 0 aa

= a ² J ( a ² - x ² ) d x - J ( a ² - x ² ) x ² d x .       (12)

Приравнивая правые части равенств (11) и (12), получаем a

J ( a ² - x ² ) x ² d x = 0

a

= a ² J ( a ² - x ² ) d x - ( 2 a ) ’ n ⁺ 3 /(2 W ( n + 1 ) ) .    (13)

Подставляя (9) в (13), получаем

J ( a ² - x ² ) n x ’d x =

= a ² ( 2 a ) ’ n * ' /( 2 ( 2 n + 3 ) W ( n ) ) .

Подставляя (14) в (10) получаем

M ( 2, a , n ) =

.

2 n + 3

Заметим, что в [8, с. 101] формула (15) представлена без доказательства и без ссылки на источник. Поэтому выполненный здесь вывод формулы (15) имеет смысл учебного примера применения формулы (9). Далее аналогично будут получены и другие формулы.

Для сравнения вычислим дисперсию среднего арифметического:

m

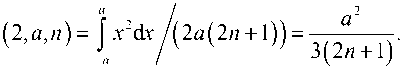
Сравнивая (15) и (16), видим, что за наше желание защититься от чрезмерных выбросов результирующего значения, получаемого от набора датчиков, природа обязывает нас платить либо избыточным количеством датчиков (но не более чем в 3 раза), либо увеличенным разбросом значений. Это при том, что для получения формулы (15) было поставлено условие: статистический разброс измеряемых значений происходит пока одинаково для всех датчиков, без смещений.

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ В УСЛОВИЯХ ДРЕЙФА

Для равномерного распределения смещенная плотность вероятности имеет вид p (a, x + L ) = У (2a)   при (-a - L) < x < (a - L);

p ( a , x + L ) = 0

[ x <  ( - a - L ), при <

[ x >  ( a - L ).

В этих условиях, учитывая известные свойства математического ожидания [10, c. 100], для сравнения запишем математическое ожидание среднего арифметического:

m ( 1, a , n , L ) =---—.             (18)

^{V 7}     2 n + 1

Учитывая известные свойства дисперсии [10, с. 103–105], нетрудно убедиться, что дисперсия среднего арифметического не зависит от L , остается постоянной в виде (16).

БАЗОВЫЕ ФОРМУЛЫ МЕДИАНЫ В УСЛОВИЯХ ДРЕЙФА

Обозначим K — порядок вычисляемого момента: 1 — для математического ожидания, 2 — для дисперсии.

В отличие от формул (1)–(4), теперь интеграл состоит из трех слагаемых, соответствующих трем вариантам получения значения от дрейфующего датчика в сравнении с медианой:

M ( K , a , n , L ) = R₁ ( K , a , n , L ) + R ₂ ( K , a , n , L ) +

+ R з ( K , a , n , L ) . (19)

• 1)    Значение от дрейфующего датчика оказалось медианой :

( 2 n ) !

R (K, a, n, L ) = ^-2- x n!

x J P ( a , X ) ⁿ ( 1 - P ( a , X ) ) n p ( a , X + L ) X K dX . (20)

-to

• 2)    Значение от дрейфующего датчика оказалось больше медианы :

, x       (2 n)!

R 2 (K , a, n , L ) =      \x,X n!(n -1)!

to

X J [P(a,X)n (1 - P(a,X))n—1 (1 - P(a,X + L)) x x p (a, X) XK ] dX.                         (21)

• 3)    Зна чение от дрейфующего датчика оказалось меньше медианы :

Rз(K,a,n,L) = (2n)! j [P(a,X)n-1 x n!(n -1)! -toL x 7

x ( 1 - P ( a , X ) ) n P ( a , X + L ) p ( a , X ) X K ] d X . (22)

Формулы (19)–(22) справедливы для любой формы плотности распределения.

ФОРМУЛЫ МОМЕНТОВ

Обозначим:

V ( n ) =------- ^{( 2} n ^{) !}       .           (23)

² n ^{+ 1}

n ! ( n - 1 ) ! ( 2 a )

С учетом смещения, указанного в (17), формулы (20)–(22) приобретают вид:

R 1 ( K , a , n , L ) = V i n i - ( a ² - X ² ) n X K d X ,   (24)

n -- a

R 2 ( K , a , n , L ) =

= V ( n ) J ( a ² - X ² ) n - 1 ( a + X )( a - L - X ) X K d X , ⁽²⁵⁾ - a

R 3 ( K , a , n , L ) =

= V ( n ) J ( a ² - X ² ) n - 1 ( a - X )( a + L + X ) X K d X +

- a

a

+ 2 aV ( n ) J ( a ² - X ² ) n ^-( a - X ) X K d X .     (26)

a - L

Подставляя (24)–(26) в формулу (19), получаем:

a - L

M ( K , a , n , L ) = V ( n ) J ( a ² - X ² ) n - 1 x

- a x a-----+ 2(a2 - X2 - LX\ IXKdX + к n                      7

a

+ 2 aV ( n ) J ( a ² - X ² ) n ^-( a - X ) X K d X .         (27)

a - L

Рассмотрим и другой вид этого выражения:

M (K, a, n, L ) = a - L

= ^{V ( n} ) J ( a a

- a

n

- X2) I - + 2 I XK dX - к n 7

a - L

- 2 LV ( n ) J ( a ² - X ² ) n - 1 X K ^{+ 1} d X + - a

a

+ 2aV(n) J (a2 -X2)n-(a -X)XKdX.(28)

a - L

Для математического ожидания, т. е. при K= 1, формула (28) имеет вид:

a - L               f 1\

M ( 1, a , n , L ) = V ( n ) J ( a ² - X ²) n I ¹ + 2 I X d X -

--a               кn7

a - L

- 2 LV ( n ) J ( a ² - X ² ) n - 1 X ² d X + - a

a

+ 2 a 2V (n) J (a2 - X2) n-1 XdX - a - L

a

• - 2 aV ( n ) J ( a ² - X ² ) n - 1 X ²d X .   (29)

a - L

Как и следовало ожидать, при L=0  получа- ется

M ( 1, a , n ,0 ) = 0.              (30)

Детально расписывать формулу (29) в общем виде здесь не будем, ограничимся рассмотрением двух частных случаев, при которых оказывается возможным применить формулу (14).

При L=a получаем

M ( 1, a , n , a ) =

a ( G ( n ) - 1 )

2 n + 1

Здесь обозначена поправка, являющаяся отличием формулы (31) от формулы (18):

( 2 n + 1 ) !

2 ^{2 n + 2} n ! ( n + 1 ) !"

Нетрудно получить рекуррентную формулу

• G ( n ) = G ( n - 1 )( 2 n + 1 )/( 2 n + 2 ) .      (32)

Для примера запишем несколько уменьшающихся значений:

1            3             5             35

G ^{( 0 )}- 4. G ⁽ i ) - 16; G ^{( 2 )}- 32; G ^{( 3 )}- 256"

Как видно, математическое ожидание медианы всегда лучше, чем математическое ожидание среднего арифметического. Но при небольшом дрейфе (в пределах полуширины статистического разброса) получаемое улучшение является незначительным, уменьшающимся по мере роста количества используемых датчиков.

При L - 2 a формула (29) c применением формулы (14) приобретает вид

M ( 1, a , n ,2 a ) -- a) ( 2 n + 1 ) .       (33)

Сравнивая (33) и (18), мы видим, что, когда измерения от дрейфующего датчика дошли до границы диапазона статистического разброса, математическое ожидание медианы в 2 раза лучше, чем математическое ожидание среднего арифметического. Очевидно, что при дальнейшем дрейфе медиана не ухудшается (в отличие от среднего арифметического).

Также понятно, что это значение математического ожидания медианы совпадает со значением математического ожидания среднего арифметического для случая L - a , поэтому ниже в разделе "Результаты вычислений…" в таблице соответствующие две колонки представлены как одна общая колонка.

ПРОИЗВОДНЫЕ МОМЕНТОВ

Рассмотрим производную выражения (28) по смещению L . По правилам вычисления производной по пределам интеграла получаем:

M l ( K , a , n , L ) -

- - V ( n )( a - L ) K ( a ² - ( a - L ) ² ) |— + 2 '                  ’ I n

+ 2 LV ( n )( a - L ) K ^{+ 1} ( a ² - ( a - L ) ² ) n - 1 +

+ 2 aV ( n )( a - L ) K ( a ² - ( a - L ) ² ) ( a - ( a - L ) ) "

При L= 0:

M _L ( K , a , n ,0 ) - - 2 V ( n ) j ( a ² - X ² ) n - 1 X K ^{+ 1} d X . - a

При L=a :

M _L ( K , a , n , a ) - M _L ( K , a , n ,0 ) /2"

При L=2a :

ML (K,a,n,2a)- 0"(34)

Для математического ожидания медианы (при K= 1), применяя формулу (14), получаем:

Ml (1, a, n ,0)- -----,(35)

2 n + 1

- 1

M, (1,a,n,a)- —-------"(36)

^{LV !} 2 ( 2 n + 1 )

В дополнение к непосредственным вычислениям графика функции по формуле (29), рассматривая простые формулы (30)–(36) вычисления значения функции и ее производных в трех точках, имеем возможность лучше понять ее характер.

ДИСПЕРСИЯ МЕДИАНЫ

Полное множество событий дает нам возможность на основе формулы (27), задавая индекс n + 1, записать следующее уравнение при K - 0:

M ( 0, a , n + 1, L ) - 2 aV ( n + 1 ) x

a x j (a2 -X2)(a2 -X2)n-1 (a -X)dX + a - L a - L

+ V ( n + 1 ) j ( a ² - X ² )( a ² - X ² ) n - 1 x

- a

x

f 0 2^ X 2

I n + 1

+ 2 ( a ²

- X ² - LX ) I d X - 1"

В этом выражении просматриваются моменты (при K - 0 и при K - 2), задаваемые той же формулой (27):

a - L

- 2 V ( n ) j ( a ² - X ² ) n ^{- 1} X K ^{+ 1} d X +

- a

V ( n + 1 )

11 — n + 1 n

a - L j ( a ’

- a

-s \ n +1

- X ² )   d X +

+

a ² M ( 0, a , n , L ) - M ( 2, a , n , L )

лы (38) аналогично получаем

V (n)

.

Учитывая, что полное множество событий дает нам M ( 0, a , n , L ) = 1, в следующем шаге преобразования получаем:

a 2( 2 n + 2)

M ( 2, a , n , a ) = ----- Ц.       (39)

v 7 (2 n +1)( 2 n + 3)

Подставляя (31) и (39) в формулу вычисления дисперсии [10, с. 103], получаем:

4< n L+ V     a - L ( a 2 - , 2 ) n -d r =

V (n +1) n (n +1) -a            '

= a ² - M ( 2, a , n , L ) .

Формулу (23) перепишем со смещенным индексом:

M ( 2, a , n , a ) - M ( 1, a , n , a ) ² =

2 n + —2(G (n)-1)2

2       2 n + 3 ^{v 7}

C a                                                              .

(2 n +1)

, _x        (2 n + 2)!

V (n +1) =------------- . ^ .

^{2 n} + 3 n ! ( n + 1 ) ! ( 2 a )

Имеющееся в (37) отношение приобретает вид

Для случая L= 2 a , т. е. когда функция плотности вероятности значений дрейфующего измерителя сместилась за пределы диапазона разброса значений всех других измерителей группы, из формулы (38) получаем

M ( 2, a , n ,2 a ) = a ² /( 2 n + 1 ) . (41)

V ( n ) _ 2 naa

V ( n + 1 ) 2 n + 1

Окончательно из (37) получаем:

Подставляя (33) и (41) в формулу вычисления дисперсии [10, с. 103], получаем

M ( 2, a , n , L ) = a ² V ( n )

M ( 2, a , n ,2 a ) - M ( 1, a , n ,2 a ) 2 = 2 na ₂ .      (42)

( 2 n + 1 ) 2

2 n + 1 n ( n + 1 )

a - L j (a2 - X2) n+1dX.

- a

Для случая L= 0 с учетом симметричности (четности) подынтегрального выражения, переписывая формулу (9) со смещенным индексом и подставляя в (38), нетрудно убедиться, что, как и следовало ожидать, получается формула (15).

Для случая L=a , т. е. когда функция плотности вероятности значений дрейфующего измерителя сместилась на половину своей ширины, из форму-

Разность между (42) и (15) составляет

₂      2 n - 1

a ²

( 2 n + 1 ) 2 ( 2 n + 3 )

и позволяет нам заметить, что по мере дрейфа одного из датчиков дисперсия медианы увеличивается.

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ ПО ПОЛУЧЕННЫМ ФОРМУЛАМ

В таблице представлены значения математического ожидания (МО) и среднеквадратического отклонения (СКО) медианы и среднего арифметического (СА) для нормированного диапазона случайных чисел равномерного закона распределения (считаем, что a = 1).

Параметры медианы и среднего арифметического для равномерного закона распределения

+ ГЯ II	МО			СКО
	Медиана	Медиана, СА	СА	Медиана			СА
	a	2 a (медиана), a (СА)	2 a
				0	a	2 a
3	0.27083	0.33333	0.66667	0.44721	0.43968	0.47140	0.33333
5	0.16875	0.,20000	0.40000	0.37796	0.37809	0.40000	0.25820
7	0.12333	0.14286	0.28571	0.33333	0.33433	0.34993	0.21822
9	0.09744	0.11111	0.22222	0.30151	0.30252	0.31427	0.19245
11	0.08066	0.09091	0.18182	0.27735	0.27823	0.28748	0.17408
13	0.06887	0.07692	0.15385	0.25820	0.25894	0.26647	0.16013
15	0.06012	0.06667	0.13333	0.24254	0.24317	0.24944	0.14907
17	0.05337	0.05882	0.11765	0.22942	0.22996	0.23529	0.14003
19	0.04799	0.05263	0.10526	0.21822	0.21868	0.22330	0.13245
21	0.04361	0.04762	0.09524	0.20851	0.20892	0.21296	0.12599

ВЫВОДЫ

• 1.    Отношение математического ожидания медианы МО мед к математическому ожиданию среднего арифметического МО СА достигает уровня 1/2, когда функция распределения дрейфующего датчика выходит за пределы функций распределения других датчиков.

• 2.    При этом суммы МО мед + СКО мед и МО_СА + СКО_СА оказываются приблизительно одинаковыми, отличающимися в пределах 15 %. Это означает, что в условиях существования дрейфа использование медианы с ее свойством более широкой дисперсии не только оправдано, но и не создает для пользователя ощущения снижения качества получаемой информации.

• 3.    На основе полученных формул и результатов вычислений предоставляется возможность формировать экспертное мнение о необходимом количестве датчиков.