Свойства медианы с учетом дрейфа одного из группы измерителей при нормальном распределении

Настоящая статья является продолжением и развитием темы нашей предыдущей статьи [1]. Предметом изучения, как и там, является ситуация с некоторым нечетным количеством одинаковых датчиков, регистрирующих радиацию, и дрейфом чувствительности одного из них. Анализируются способы оценки измерений. В [1] рассмотрены свойства медианы для равномерного (прямоугольного) распределения плотности вероятности значений, получаемых от каждого измерителя (датчика), в условиях дрейфа чувствительности одного из группы измерителей. Равномерное распределение позволило вычислить требуемые интегралы аналитически точно. Но на практике мы имеем дело с данными, которым свойственно распределение Пуассона. Как известно, оно мало отличается от нормального распределения, являющегося более удобным для математических выкладок. В данной статье для нормального распределения получены формулы математического ожидания и дисперсии медианы в условиях дрейфа одного из группы измерителей. Однако эти формулы являются приближенными, поэтому для их уточнения введены поправочные функции, полученные сравнением с результатами численного интегрирования.

БАЗОВЫЕ ФОРМУЛЫ

Пусть задана функция p(a,x) — плотность вероятности распределения измеряемой величины x в области значений, ширина которой характеризуется параметром a.

Запишем и интегральную функцию вероятности распределения:

X

P ( a,X ) = J p ( a,x ) d x .

-to

Обозначим N количество чувствительных элементов (датчиков). Ограничимся вариантом нечетного набора: N = 2 n + 1.

Обозначим L величину дрейфа в сторону занижения. Это значит, что плотность вероятности приобретает вид p ( a , x + L ).

Начнем с рассмотрения исходного состояния, когда L = 0. Формулы для этого случая известны из [2, с. 17–18], [3, c. 96].

Вероятность получения значения медианы в интервале от X до X + d X

Q ( a , n , X ) d X =

= W ( n ) P ( a , X ) n ( 1 - P ( a , X ) ) n p ( a , X ) dX .    (1)

Здесь мы имеем "перестановки с повторениями" [4, с. 48], количество которых определяется мультиномиальным коэффициентом

, x (2n +1)! W (n ) = ("nT)" ■

Формула моментов порядка K (для вычисления математического ожидания и дисперсии) имеет вид:

M ( K , a , n ,0 ) = j Q ( a , n , X ) X K dX .     (2)

-to

При наличии дрейфа формула вычисления моментов порядка K имеет вид суммы трех слагаемых, соответствующих трем вариантам получения значения от дрейфующего датчика в сравнении с медианой

M ( K , a , n , L ) = R 1 ( K , a , n , L ) +

+ R ₂ ( K , a , n , L ) + R з ( K , a , n , L ) .    (3)

• 1)    Значение от дрейфующего датчика оказалось медианой :

R i ( K , a , n , L ) =

= -—2^ j P ( a , x ) n ( 1 - P ( a , x ) ) n p ( a , x + L ) x K d x . (4) ⁿ * -to

• 2)    Значение от дрейфующего датчика оказалось больше медианы :

R 2(K, a, n, L) = —(—)— j [ P (a, x) n x n!(n-1)!-toL

x(1 -P(a,x))n i (1 -P(a,x + L))p(a,x)xK Jdx.(5)

• 3)    Значение от дрейфующего датчика оказалось меньше медианы :

R з (K, a, n, L h^2^ П P (a, x) n-1 x n!(n-1)!-toL 7'

x(1 - P (a, x))n P (a, x + L) p (a, x) xK J dx.

ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ

Для начала проанализируем производные по параметру L . Они пригодятся в дальнейшем для повышения точности формул:

-d- R (K, a, n, L ) = dL

= -—2^ j P ( a , x ) n ( 1 - P ( a , x ) ) n —p ( a , x + L ) x K d x .

n !                             d x

-to

Имея в подынтегральном выражении производную по параметру x , совпадающую с производной по параметру L , выполним интегрирование "по частям". Множитель x^K не мешает обнулению в бесконечности, поэтому получаем:

-d- R1 (К, a, n, L ) = dL

• =---- J [ nP ( a , x ) n 1 p ( a , x ) x n ,      -to-

• x ( 1 - P ( a , x ) ) n p ( a , x + L ) x K J d x +

+-—J Г P (a, x) n n x n!2

-to

• x ( 1 - P ( a , x ) ) n 1 p ( a , x ) p ( a , x + L ) x^K J d x -

• - -—2^ j P ( a , x ) n ( 1 - P ( a , x ) ) n p ( a , x + L ) Kx K ^-1 d x . ^{n !} -to

В полученном выражении первые два интеграла, рассматриваемые с обратными знаками, полностью совпадают с производными выражений (5) и (6) по параметру L . Поэтому после сокращений остается только один интеграл

2 n !

—M (K, a, n, L ) = - K ^)-x dL ( , , , )          n !2

to x j P(a, x)n (1 - P(a,x))n p (a,x + L)xK-1dx.    (7)

-to

В частности, при L = 0 и K = 1 полученная формула (7) похожа на формулу (2) при K = 0, которая при этом тождественно равна единице. Поэтому, учитывая отличие коэффициентов, получаем d                 -1

— M ( K , a , n ,0 ) =  --- -.            (8)

d L              2 n + 1

Это означает, что при малых значениях дрейфа математическое ожидание медианы совпадает с математическим ожиданием среднего арифметического

Mmean (K, a, n, L ) = ——.(9)

2 n + 1

На основе формулы (7) далее запишем и вторую производную:

M (K, a, n, L ) = - K ^-x dL2

to x j P(a,x)n (1 - P(a,x))” —p (a,x + L)xK-1dx.

В частности, при K = 2 для нормального распределения в Приложении обосновывается получение формулы (10):

— M ( 2, a , n ,0 ) =  --- -^M ( 2, a , n ,0 ) .   (10)

d L                ( 2 n + 1 ) a

НАЧАЛЬНОЕ ПРЕОБРАЗОВАНИЕ ФОРМУЛ ДЛЯ ИНТЕГРИРОВАНИЯ

Далее нам будет удобнее пользоваться следующими обозначениями:

P ( a , x ) = 2 ( 1 + Ф ( a , x ) ) ,            (11)

Заметим, что R 4 не зависит от L и может быть выражено как

R ₄ ( K - a - n ) = ( 2 n - 1 ) R 1 ( K - a - n - 1-0 ) .    (19)

При K = 1 нечетность подынтегрального выражения порождает тождество

R ₄ ( 1, a , n ) = 0.

p ( a , x ) = 2Ф * ( a , x ) .                (12)

Предельные значения пригодятся при интегрировании: Ф ( a , -да ) = - 1- Ф ( a , r ) = 1.

Формула (2) приобретает вид:

M ( K , a , n ,0 ) =

= (2^+^! j (1 — Ф2 (a-x))"p(a-x)xKdx•

Формулы (4)–(6) приобретают вид:

R ( K , a , n , L ) =

(2")! Г Л 2л /      " i

= 4" ,- j (1 — Ф (a-x)) P(a-x + L)x dx,(14)

" -Г

Приступим к преобразованию интеграла R5. Учитываем, что p (a - x ) = 2Ф*( a - x) -

Ф * ( a - x + L ) = 2 p ( a - x + L ) .

Интегрируя по частям, получаем

2 n !

R ( K - a - n - L ) =--- ⁽_z ) x

^{5 (}            ) 4 " n !( n - 1)!

X<

2 " [^{( 1} - Ф 2 ⁽ a - x

I Ф ( a - x + L ) x^K

1Г

-Г

—

^R 2 ^{( K} , " ¹ " , ^L ) = ₄ "^^{П )}_-i_{) !} Ш' — Ф ⁽ a , x Я " -^X

x ( 1 + Ф ( a , x ) )( 1 - Ф ( a , x + L ) ) p ( a , x ) x K J d x , (15)

- ¹ j ( 1 - Ф ² ( a - x ) ) " p ( a - x + L ) x^K d x -

" -„

Г

-— j ( 1 - Ф ² ( a - x ) ) Ф ( a - x + L ) x^K 1 d x > .

^R 3 ^{( K} - a - " - ^L ) = 4 " 2 " ^ )■ Ш^{1 -} Ф ^{2 (} a - ^x» " - ^{1 X}

x ( 1 - Ф ( a , x ) )( 1 + Ф ( a , x + L ) ) p ( a , x ) x^K J d x . ⁽¹⁶⁾

При сложении величин R 2 и R 3 , раскрывая скобки, обнаруживаем возможность сокращения слагаемых, поэтому получаем

В этом выражении при подстановке пределов интегрирования получается ноль, а первый из двух интегралов по абсолютной величине совпадает с интегралом R 1 ( K , a , n , L ) и сокращается с ним. Поэтому получаем

M ( K - a - n - L ) = R 4 ( K - a - n ) - R ₆ ( K - a - n - L ) .   (22)

Здесь обозначено

R ₂ ( K , a , n , L ) + R ₃ ( K , a , n , L ) = = R ₄ ( K , a , n , L ) + R ₅ ( K , a , n , L ) .

Здесь обозначены:

R 4 ( K , a , n , L ) =

2 ( 2 n ) !    Г/               .x n -1

----——— [ (1 - Ф² ( a , x )) p ( a , x ) x^K d x , 4 " n ! ( n - 1 ) !-/        ^{v - v - }       -}

R 6 ( K - a - n - L ) =

= ^K 2 2 2 + " ^! 2 j ( 1 ^- Ф ² ( a ^{- x} ) ) " ^Ф ( a ^{- x + L} ) x^K - ^{1 d x} .

" -Г

Заметим, что dR K,a,n,L

^{6 ( - - -} ) = KR ( K - 1- a - n - L ) .

d L            ¹

R(K - a - ” - L ) = 4 "~п2( 2-1)! Й(1 - Ф2 (a,x»n -X x Ф (a, x) Ф (a, x + L) p (a, x) xK J dx. (18)

ФОРМУЛЫ ДЛЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

В полученных формулах (22)–(24) может быть произвольная гладкая функция плотности распределения. Теперь возьмем нормальное распределение:

Р (a, x)

a 2π exp

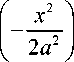
2 , I , v I ux + vx = u I x + — I к     2 u )

-

v ²

4 u

.

Ф ( a , x ) = erf I - x - I . к \- a )

Для нашего случая обозначим:

u =

4 n + n

Используемая функция Лапласа (функция ошибок) имеет вид

2 πa ²

L v = 2". a2

Тогда

erf ( x ) = -2= f exp ( - t ² ) d t .

π 0

Известна приближенная формула [5]:

v

πL

2 u 4 n + n ’

v ²

n L²

v ²

_2 Г 2

П L

erf ( x )

1 - exp

"     4

- + yx

-x2 ПГ

1 + yx ²

к)

Здесь обозначено:

_Y = 8 ( 3 - * ) .

3 п ( n - 4 )

Столь громоздкая формула нам никак не поможет брать интегралы аналитически. Поэтому воспользуемся менее точным, но вполне приемлемым вариантом у = 0 •

По аналогии, как в [3, с. 103–104] записана приближенная формула плотности вероятности медианы, здесь мы получим приближенные формулы математического ожидания и дисперсии медианы в условиях дрейфа одного из группы измерителей.

Формула (26) с учетом (27) приобретает вид

Ф ( a , x )

- 1 - exp

l v '¹

2 I . к na )

При этом появляется возможность записать весьма удобную формулу:

1 - Ф ² ( a , x ) = exp

f-I

2 I . к ^{n a} )

Формула (14) с учетом (25) и (28) приобретает вид:

R , ( K , a , n , L ) =

( 2 n )!

4 ⁿ n ! ² a 2 π

exp

- I к 2 a ² )

d             -.2

r x f 2 n 1 I xL I z™\

X exp —- — + - —- x K d x . ⁽²⁹⁾

-к к a к n 2 ) a )

Чтобы взять этот интеграл, надо сначала записать полином в удобном виде по формуле

4 u   2 a ² ( 4 n + n ) ’ 4 u ²    ( 4 _n + л ) ²

Воспользуемся также свойствами функции вероятности нормального распределения:

x f exp

—

к

Cd f exp

-d

Cd

,2

-

к 2 a

f x- I 2 exp--- x d x = a

, к ^{2 a} )

,2

³ 2 π .

,

Выполняя замену переменной x путем смещения на величину (31), используя (30), (32) и (34), перепишем формулу (29) при K = 0 в следующем виде:

2 n !

R (0, a , n , L) = J -------exp ^{1 (}        ) 4 n n^4n + n  ^p

2 nL²

a ² ( 4 n + n )_v

По формуле (19) сразу же запишем:

R ₄ ( 0, a , n ) = ( 2 n - 1 ) R 1 ( 0, a , n - 1,0 ) =

= ( 2 n - 1 ) !           n

= 4 n -¹ ( n - 1 ) !²\4 ( n - 1 ) + n"

На основе формулы (24) при K = 1 выполняем интегрирование по формуле (33) :

R 6 ( 1, a , n , L ) =

( ² n ) ^! na ^f L I 2 n

2 + n ! v2 n ^erfl a 41+ . )

+ c 1 .

Для формулы (29) при K = 1, выполняя замену переменной путем смещения на величину (31), обнаруживаем, что смещение приобретает роль множителя:

- nL

R 1 ( 1, a , n , L ) =  ------- R 1 ( 0, a , n , L ) =

4 n + n

( 2 n ) ! L ( n ) 2     Г      2 nL²    )

= -    1 4 П 7 П J ^exp V- O^n J

По формуле (19) сразу же запишем:

R ₄ ( 1, a , n ) = ( 2 n - 1 ) R 1 ( 1, a , n - 1,0 ) = 0.

На основе формулы (24) при K = 2 выполняем интегрирование, получаем

, _x 2 ( 2 n - 1 ) !

R ₆ ( 2, a , n , L ) = na ²  ----- x

⁶                           4 ⁿ n ! ²

x

π

4 n + n

exp

V V

2 nL²

a ² ( 4 n + n )_y

^

^{1 +} c 2 .

J

Константу c 2 определим на основе исходного значения дисперсии по формуле (22) при K = 2, L = 0. Заметим, что R 6 (2, a , n , 0) = c 2 , поэтому получаем уравнение

M ( 2, a , n ,0 ) = R ₄ ( 2, a , n ) - c ₂.

Это означает, что можно взять c 2 = 0, но при этом надо вместо R 4 (2, a , n ) брать M(2, a , n , 0), вычисляемое на основе формулы (2).

Формула (3) при L = 0 полностью совпадает с формулой (2), однако при использовании приближенных выражений вероятности совпадение этих формул неизбежно получается также приближенным.

Подставляя (25) и (28) в (1) и (2), применяя (35), получаем

Для формулы (29) при K = 2, выполняя замену переменной путем смещения на величину (31), обнаруживаем два ненулевых слагаемых, вычисляемых по формулам (34) и (35). При этом квадрат смещения приобретает роль множителя

M ( 2, a , n ,0 ) =

( 2 n + 1 ) !

a 2 π 4 ⁿ n ! ²

x

R , ( 2, a , n , L ) =

( ² n ) ^!

4 ⁿ n ! ² a 2 π

x

to x J exp

-to

Г x ² Г, 4 n )) ₂,     ₂

--- 1 + — x d x = a

V 2 a V n J J

( 2 n + 1 ) ! Г n   ^ 3

4 n n ! ² V 4 n + n J

x exp

Г   L²

_v 2 a ^{2 +}

πL ²

2 a ² ( 4 n + n )_v

_x2 na ³ Г       ) 2

V 4 n + n J

+

( 2 n ) ! I П

+

4 nn ! ² v 4 n + n

exp

2 nL²    ) n ² L²

a ² ( 4 n + n ) J ( 4 n + n ) 2"

Полному множеству событий соответствует тождество M(0, a , n , 0) = 1. Однако при использовании приближенных выражений вероятности это равенство соблюдается также приближенно.

Подставляя (25) и (28) в (1) и (2), применяя (35), получаем

Эти слагаемые можно объединить:

R 1 ( 2, a , n , L ) =

( 2 n ) ! Г n ^ 2 4 n n ! ² V 4 n + n J

M ( 0, a , n ,0 ) =

( 2 n + 1 ) ! ^to _r

=  ,—  — exp a^2П4nn!2 -to

V

x ² Г, 4 n )V --т 1 + — d x =

2 a ²      π

x exp

V

x

2 nL²   "

a ² ( 4 n + n )_y

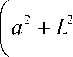
π

4 n + n

= ( 2 n + 1 ) ! ГП

4 n n ! ² \4 n + n

.

Однако полученное выражение нам требуется только при L = 0:

R 4 ( 2, a , n ) = ( 2 n - 1 ) R ( 2, a , n - 1,0 ) =

= a

( 2 n - 1 ) ! Г n ) 4 " - ¹ ( n - 1 ) ! ² V 4 ( n - 1 ) + n ,

Каждый из интегралов, вычисленных здесь приближенно, имеет ошибку, близкую к ошибке вычисления интеграла M(0, a , n , 0). Поэтому для повышения точности формул выражение (38) можно использовать в качестве поправочного коэффициента-делителя. В [3] использование этого коэффициента называется нормировкой. При этом получаются выражения более удобные (без факториалов).

Запишем только три требуемых выражения:

Приступим к вычислению констант, появившихся при интегрировании.

Константу c ₁ определим на основе исходного значения математического ожидания по формуле (22) при K = 1, L = 0:

R 6 ( 1, a , n , L ) =

Taa    1 4 n + n

2 ( 2 n + 1 )\ 2 n

Г erf L

V a

2 n

4 n + n

, (39)

J

M ( 1, a , n ,0 ) = 0 = R 4 ( 1, a , n ) - R 6 ( 1, a , n ,0 ) .

Учитывая (36), получаем c 1 = 0.

R 6 ( 2, a , n , L ) =

πa ²

2 n ( 2 n + 1 )

exp

V

—

V

2 nL ²

a ² ( 4 n + n )

—

J

1 , (40)

J

M ( 2, a , n ,0 ) =

πa ²

4 n + n

M 2 n ( 1, a , n ) =

^- ( ² n ) '    _x

2 2* n ! ( n - 1 ) !

ВЫЧИСЛЕНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

В соответствии с формулой (22) выражение (39), взятое со знаком минус, определяет математическое ожидание медианы M(1, a , n , L ).

В частности, при малых значениях L , разлагая (39) в ряд по известной формуле [6, с. 119], обнаруживаем, что первый член ряда совпадает с (9).

Рассмотрим также асимптотику математического ожидания

- ^na /4 n + n

^M ( 1, a , n , ^{да )} =                 ---- .        (42)

2 ( 2 n + 1 ) V 2 n

Очевидно, что при L ^ да мы имеем право полностью игнорировать дрейфующий датчик. Поэтому асимптотическую величину (42) уместно сравнить с математическим ожиданием центральной (с индексом n –1 или n ) порядковой статистики на множестве 2 n датчиков. Для этого воспользуемся формулой из [7, с. 96], запишем формулу момента K -го порядка в следующем виде:

, X (2 n )!

M2n (K, a, n ) = z L X n!(n -1)!

да x j P(a, x)n 1 (1 - P(a,x))n p (a,x)xKdx.(43)

-да

С учетом формулы (11) имеем

2 n !

M2„ (K, a, n) = 7    /--- x

² n ⁽          ) 2 2 ^{n - 1} n ! ( n - 1 ) !

да xj(1 - Ф2 (a, x)) (1 - Ф (a, x)) p (a, x) xK dx.

-да

Множитель (1 – Ф( a , x )) дает возможность выбирать из него только одно слагаемое (в зависимости от K ), при котором подынтегральное выражение будет четным.

В частности, сравнивая (13) и (44), нетрудно убедиться, что справедливо тождество

M 2 n ( 2, a , n ) = M ( 2, a , n - 1,0 )           (45)

и имеем дисперсию нормального распределения

M₂ n ( 2, a ,1 ) = M ( 2, a ,0,0 ) = a ² .         (46)

Учитывая (12), для математического ожидания (при K = 1) получаем выражение, интегрируемое по частям:

да                                          i x j (1 -Ф2(a,x))   Ф(a,x)Ф*(a,x)xdx =

-да

- ( 2 n ) ! г /       ~ ,      ₄\«

=        ₂ [ (1 - Ф² ( a , x )) d x .

2^{2 n + 1} _n !² J ^v '

-да

Пользуясь приближенной формулой (28) и точной формулой (34), получаем

M 2 n ( 1, a , n ) =

- ( 2 n ) ! na

2 ² n ^{+ 1} n ! ²

.

2 n

На основе (44) запишем выражение, соответствующее полной вероятности (при K = 0):

M 2 n ( 0, a , n ) =

( ² n ) '          _x

2 ² " ^{- 1} n ! ( n - 1 ) ! a 42П

да x j (1 - Ф2 (a, x)) exp

-да

к

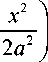
Пользуясь приближенной формулой (28) и точной формулой (34), получаем:

M₂„ (0, a , n ) = ₂ ,⁽² n ^)! , ---П .   (48)

² n ⁽        ) 2 ^{2 n - 1} n ! ( n - 1 )Ц| 4 ( n - 1 ) + n     ^V ’

Формулу (47) перепишем с учетом нормировки, т. е. выполняя деление на (48):

M 2 n ( 1, a , n ) =

V na /4 ( n - 1) + n 4 n       2 n

Разницу между приближенными выражениями (42) и (49) можно считать оценкой их точности. А чтобы найти ответ на вопрос о том, какое из них предпочтительнее, целесообразно выполнить численное интегрирование формулы (43) при K = 1 с использованием (25) и (26).

Между тем, при наличии результатов численного интегрирования необходимость использования формул (42) и (49) отпадает. Принимая во внимание их вид, теперь уместно вместо формулы (39) записать похожую формулу с поправочной функцией ф ( n ) , обеспечивающей совпадение с асимптотическими значениями, которые получены численным интегрированием. При этом соблюдаем требование: при малых значениях параметра L формула должна совпадать с (9)

R 6 ( 1, a , n , L ) =

Паа I 4 n - ф ( n ) 4 n      2 n

erf

I

2 nL       2 n

( 2 n + 1 ) a у 4 n - ф ( n ) ^

В табл. 1 представлены значения поправочной функции ф ( n ) , а в табл. 2 — набор значений функции R 6 (1, a , n , L ), вычисленных по формуле (50). Для сравнения под каждым значением указан результат численного интегрирования.

В нижней строке табл. 2 для каждого значения L указан результат вычисления интеграла полной

вероятности, который должен быть равен единице. По мере увеличения L происходит занижение результата численного интегрирования, т. к. в численном эксперименте "хвост" распределения дрейфующего датчика постепенно уходил за границы интервала интегрирования. Очевидно, что и другие результаты численного интегрирования, представленные в соответствующих колонках, занижены в той же мере. Тем не менее из табл. 2 видно, что формула (50) вполне удовлетворительна.

Табл. 1. Поправочная функция φ ( n ) для формулы математического ожидания медианы

Функция	Число N датчиков
	3	5	7	9	11	13	15
φ	0.75772	0.81160	0.82804	0.83729	0.84038	0.84398	0.84578

Табл. 2. Математическое ожидание медианы в зависимости от дрейфа одного датчика. (Формат данных: R ₆ согласно (50), R ₆ по численному интегрированию)

Число N датчиков	L/a
	0.5	1.0	1.5	2.0	2.5	3.0	1000.0
3	0.16294, 0.16291	0.30522, 0.30508	0.41373, 0.41332	0.48598, 0.48490	0.52800, 0.52451	0.54934, 0.53759	0.56419
5	0.09711, 0.09711	0.17859, 0.17856	0.23596, 0.23586	0.26985, 0.26946	0.28665, 0.28500	0.29364, 0.28761	0.29701
7	0.06915, 0.06915	0.12610, 0.12609	0.16473, 0.16468	0.18631, 0.18606	0.19624, 0.19514	0.20000, 0.19592	0.20155
9	0.05368, 0.05368	0.09743, 0.09742	0.12646, 0.12643	0.14217, 0.14199	0.14909, 0.14826	0.15157, 0.14849	0.15251
11	0.04387, 0.04387	0.07937, 0.07936	0.10261, 0.10258	0.11491, 0.11477	0.12019, 0.11952	0.12202, 0.11954	0.12267
13	0.03709, 0.03709	0.06696, 0.06695	0.08631, 0.08629	0.09642, 0.09630	0.10066, 0.10011	0.10210, 0.10002	0.10259
15	0.03213, 0.03213	0.05790, 0.05790	0.07448, 0.07447	0.08304, 0.08294	0.08659, 0.08611	0.08777, 0.08599	0.08816
Теор. значение P	Вычисленное значение полной вероятности P
P = 1	0.99999	0.99997	0.9998	0.9988	0.9946	0.9798	–

Табл. 3. Условная граница существенного преимущества медианы

Функция	Число N датчиков
	3	5	7	9	11	13	15
f L ) V a J 0.5	3.3398	2.9303	2.7839	2.7084	2.6626	2.6316	2.6094

Чтобы представить ход изменения математического ожидания медианы, найдем значение дрейфа, при котором математическое ожидание медианы становится равным половине математического ожидания среднего арифметического. Иначе говоря, запишем уравнение

0.5

L

2 n + 1

erf

4 n 2 n

2 nL

2 n )

( 2 n + 1 ) a 4 n - ф ( n )

. (51)

Удобно применить обозначение

2 nL       2 n

( 2 n + 1 ) a у 4 n - ^ ( n )

Уравнение (51) приобретает вид t = Пе erf ( t ) .

Решение этого уравнения является константой

1 0.5 = 1.748709.

Соответственно имеем erf ( 1 0 ₅ ) = 0.98660.

Это означает, что в данной точке математическое ожидание близко к своему асимптотическому значению (42). С учетом (52) получаем решение уравнения (51):

L ) = , fl + —) 2- ^n a J_{0 5}    . V    2 n Jv      2 n

Результаты вычислений по формуле (53) представлены в табл. 3. Когда величина дрейфа превышает указанные значения, медиана приобретает существенное преимущество в сравнении со средним арифметическим. При n ^ да получается предельное значение 2.4730.

УТОЧНЕНИЕ МОМЕНТОВ ВТОРОГО ПОРЯДКА

Формула (44) при K = 2 имеет вид

2 n !

M₂„ (2, a , n ) =             _x x

^{2 n (}         ) 2 2 ⁿn ! ( n - 1 ) !

x j ( 1 - Ф 2 ( a , x ) ) ⁿ '^Ч a , x ) x 2 d x .

-да

С учетом (25) и (28) можно выполнить интегрирование по формуле (35):

,       ,       a ² ( 2 n ) !     f n       ) 2 _{z x}

M ² n ⁽ 2, a , n ) = 2 2n ^{- 1} n ! ( n - 1 ) ! V 4 ( n - 1 ) + n J . ⁽⁵⁴⁾

Выполним нормировку, т. е. разделим (54) на (48), получаем

M 2 n ( 2, a , n ) = — ---- .           (55)

4 ( n - 1 ) + n

Как видно, тождества (45) и (46) справедливы и для полученных приближенных формул (41) и (55).

Выполнив численное интегрирование формулы (13) или (44) при K = 2, имеем возможность в приближенные формулы (41) и (55) добавить поправочную функцию v ( n ) . При этом удобно сделать обозначение

<у( n) =------1—.

4 n + п - v ( n )

Формулы (41) и (55) приобретают вид:

M (2, a, n ,0 ) = na 2ro( n),(56)

M2n (2,a,n) = na2ro(n -1).(57)

Значения поправочной функции v ( n ) представлены в табл. 4.

Заметим, что v ( 0 ) = 0 в соответствии с тождеством (46).

Тем самым получаем возможность в формуле (40) применить более точный коэффициент, записываемый на основе разности между значениями (57) и (56). Формула (40) приобретает вид

Табл. 4. Поправочная функция ψ для формулы момента второго порядка

Функция	Число N датчиков
	1	3	5	7	9	11	13	15
ψ	0	0.13958	0.18879	0.21362	0.22773	0.23701	0.24440	0.24777

Табл. 5. Граница предпочтительности использования медианы

Функция	Число N датчиков
	3	5	7	9	11	13	15
Г L ) V a ^ PREF	2.0119	2.0224	2.0861	2.1553	2.2228	2.2870	2.3480

z ( a , n , L )

Семейство кривых нормированной дисперсии

R 6 ( 2, a , n , L ) = na ² ( ю ( n - 1 ) - ю ( n ) ) x

= na ² x

(    ( x exp

V V

L * ( n ) )

^

1v

x

( re(n) + (®(n -1)- ю(n)) 1 - exp V

(

—

L^

V

В показателе экспоненты требуемый множитель Л ( n ) можно брать на основе приближенных формул (37) или (40). Но лучше воспользоваться уравнением (10), в которое можно подставить (56) и вторую производную от (58), т. к. именно она определяет вторую производную момента второго порядка. В итоге нетрудно получить

-

4 n - ф ( n ) 32 n ³

( erf

V

2 nL __ 2 n

( 2 n + 1 ) a 4 n n - ф ( n ) ^

Для сравнения запишем дисперсию среднего арифметического:

Л( n) =

re( n)

( 2 n + 1 ) ( ® ( n - 1 ) - ® ( n ) )

^D MEAN ⁽ a , n , ^L ) =     Г

2 n + 1

.

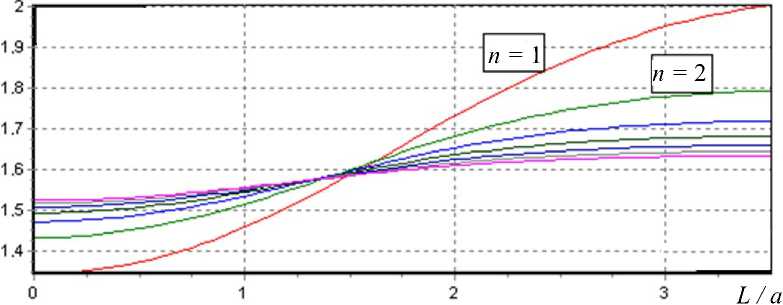
На рисунке представлено семейство кривых дисперсии медианы, деленной на дисперсию среднего арифметического

ВЫЧИСЛЕНИЕ ДИСПЕРСИИ

Пользуясь известной формулой вычисления дисперсии [7, с. 103], учитывая (22), подставляя (50), (56) и (58), получаем

D ( a , n , L ) = M ( 2, a , n , L ) - M ( 1, a , n , L ) ² = = M ( 2, a , n ,0 ) - R 6 ( 2, a , n , L ) - ( R 6 ( 1, a , n , L ) ) 2 =

z ( a , n , L ) =

D ( a , n , L ) D MEAN ⁽ a , n , ^L )

При n = 1 кривая идет наиболее круто, а по мере увеличения количества измерителей кривая становится более пологой, стремящейся к горизонтальной линии на уровне π 2 . Как видно, все кривые связаны своими точками перегиба в единый узел с координатами приблизительно (1.4, 1.6).

Улучшение математического ожидания медианы в сравнении со средним арифметическим природа дает нам ценой ухудшения дисперсии. Для ответа на вопрос о том, в какой мере оправдана такая цена, границу предпочтительности использования медианы предлагается определить как решение следующего уравнения, содержащего среднеквадратические отклонения, приравнивающего границы статистического разброса:

^M MEAN ⁽¹, a , n , ^L ) + 4 ^D MEAN ( a , n , ^L ) =

= M(1, a , n , L ) + D ( a , n , L ) .

Решение этого уравнения, полученное программированием, представлено в табл. 5.

В сравнении с табл. 3 мы видим более широкую область предпочтительности медианы.

ВЫВОДЫ

Полученные формулы и результаты вычислений предоставляют возможность оценивать параметры медианы в сравнении с параметрами среднего арифметического в зависимости от количества датчиков и от дрейфа одного датчика. Тем самым обеспечена возможность выбора количества датчиков в соответствии с задаваемыми требованиями по точности измерений случайной величины (мощности дозы).

ПРИЛОЖЕНИЕ

При K = 2 для нормального распределения, используя (25) и сравнивая с (2), получаем:

d ²                      2

■M ( 2, a , n ,0 ) = —----, , - M ( 2, a , n ,0 ) .

d L                ( 2 n + 1 ) a