Свойства пористых термостойких композиционных материалов. Часть 1

T his article is a continuation of our series of articles devoted to the production of porous composite nanomaterials. In our previous work [1], the analysis of the main types of porous heat-resistant materials was carried out. Comparison of various chemicals with the highest thermal stability and refractoriness was carried out, which made it possible to choose the objects that are most suitable for creating the corresponding composite materials. In [2, 3], an analysis was made of the structure of pores in solid porous solids. In this work, we tried to illuminate the properties of the main porous heat-resistant materials manufactured industrially. The first review devoted to such materials was released a long time ago and was devoted only to porous structural ceramics [4]. In this paper, we examined not only structural ceramics, but also functional porous materials.

Advanced porous ceramics is widely used to solve several environmental, biological and technical problems facing modern industrial technology. Ceramic materials have many advantages over other materials such as polymers or metals. They have such unique properties as hardness, wear resistance, chemical inertness, resistance to thermal shock and corrosion. The low density of such materials is a quality that is necessary for many practical applications.

To date, many different types of porous refractory materials have been developed. Industrial heat-shielding materials [4, 6–8] are classified by volume weight (kg/m3) per brand (15÷700). The coefficient of thermal conductivity for high-performance materials is in the range 0,01÷0,15 W/m•K, for low-efficiency materials up to 0,25 W/m•K.

A large group of them is occupied by foam-like materials obtained by introducing into the initial charge poreformers [9–11] or by burning out one of the components of the charge [8, 12, 13]. All these materials are characterized by a sufficiently high density from 0.5 to 1.5 g/cm3 and, correspondingly, low porosity and high thermal conductivity. A wide class of materials is known which is obtained by burning spherical powders of refractory oxides in which the porosity is achieved by adjusting the nature of the contacts and the packing density of the particles in the material. However, in this way, dense compositions with a specific gravity of 1÷2 g/cm3 are obtained [5]. At the same time, the production of spherical powders is a complex problem requiring the use of low-temperature plasma.

Higher values, in comparison with these materials, are based on various inorganic microspheres and mineral fibers. For compositions based on microspheres, a sufficiently high strength is characteristic, up to 10 MPa at a density of 0.35÷0.4 g/cm3 [7, 14, 15]. However, the technique of obtaining hollow microspheres is complicated, requiring the use of the process of blowing the melt of the formed oxide in strictly defined hydrodynamic parameters.

The most promising in terms of production are fibrous materials, since high-porosity compositions are created on their basis. A method for manufacturing refractory insulation from fibers is known. The fibers in this method are treated with aqueous solutions of chromium salts Cr(OH)SO4 and CrCl3 using NaOH and KOH precipitators [16]. The disadvantages of this material include the presence in its structure of ions of alkali metals, leading to a significant reduction in heat resistance as a result of the formation of fusible eutectics.

For example, in a number of refractory industries in Russia such types of lightweight heat-insulating refractory products as SHL-1,3, SHL-1,0 and SHL-0,4 are manufactured. In addition to these products, the refractory heat-insulating glass-fiber mullite-siliceous material of the MKRR-130 brand is produced [17]. Based on it, mullite-siliceous slabs are produced on an organic binder of the brand MKRP-340 and grade MKR1M-500 on a clay binder [17]. But these materials have a drawback – the presence of an organic binder leads to a significant decrease in their heat resistance and the appearance of a large volume of decomposition products of organic matter during operation.

The greatest successes in obtaining lightweight refractory materials were achieved in the United States as a result of the development of production and flight tests of the thermal protection system of the reusable space shuttle “Space shuttle”. Firm Rockwell International produced tiles from ceramic fiber of two types LI-900 with a density of 0.144 g/cm3 [18]. Lockheed for the Apollo spacecraft developed the LI-1500 heat-shielding material with a density of 240 kg/m3. In the future, as a result of studies to improve the characteristics of the LI-1500 material, the focus was on the chemical composition of the fiber, which led to the creation of silica fibers of high purity and an increase in the thermal stability of the LI-1500 material. Thanks to new fibers and improved processing methods, which changed their orientation, placing the binder component in the composite structure, a new heat-protective material LI-900 was created.

Based on the alumina-borosilicate fibers of Nickel 312 and the micro-quartz by the Research Center Ames has developed a new FRCI material with a few new properties [33].

1.    Physico-chemical characteristics of porous refractory materials

The physicochemical characteristics of highly porous refractory materials have been studied in detail for the FRC1 material developed by Lockheed and its laboratory. Ames [19] FRC1 is built from two types of fibers.

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

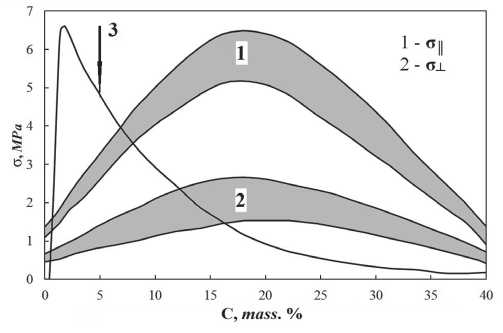
Fig. 1. Dependence of the ultimate strength on the FRCI bend (ρ = 0.32 g/cm3). 3 – content of cristobalite (%). C – Content of the ABC fiber Nextel-312 (Thick Fiber), wt. %

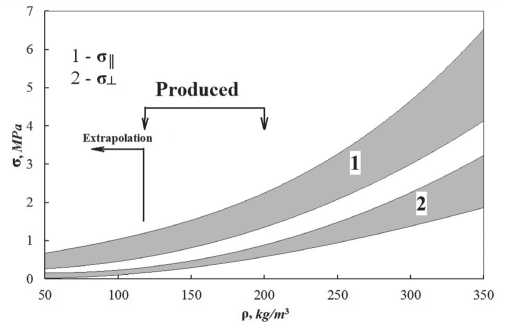
Fig. 2. Dependence of the FRCI-20 tensile strength on the break from the density

The first type of fiber is Alumina-borosilicate Nickel 312 from Manning, 11 microns in diameter and 0.31 cm long. The second type of fiber is a microsquartz of Johns Manville, 1÷3 µm in diameter. The relative strength of FRC1 material, characterized by the bending strength in directions parallel or perpendicular to the orientation of the fibers, is shown in Fig. 1. The maximum strength is achieved at 20% of the Alumina-borosilicate fiber content of Nickel Steel 312. Figure 9 also shows the stability of the morphology of the resulting material structure, characterized by the content of cristobalite after aging at 1370oC for 4 hours.

Fig. 2 shows the dependence of the tensile strength on the density value for the FRCI-20 material. At a density of 0.19 g/cm3, the tensile strength in the direction of greatest strength or orientation of the fibers is 18.5÷17.6 kg/cm2 and when stretched in the direction of the least strength or perpendicular to the orientation of the fibers, 5.0÷9.8 kg/cm2 (see Fig. 3). The elongation at failure is 0.38–0.53%, respectively, when stretched parallel to the orientation of the fibers and 0.7 to 0.9% when stretched perpendicular to the orientation of the fibers (Fig. 3) [19].

The FRCI-20 material was investigated at the Institute of Strength Problems [20]. The stress-strain-strain diagrams, the strength and elastic characteristics of the material were obtained in a wide temperature range from 20 to 1000oC for various types of loading. Figure 4 shows examples of loading diagrams.

It can be seen from these examples that when loads of samples are observed, disruption of loads with a further increase in the load is observed. Apparently during the test, the material is destroyed not simultaneously, but consistently, by breaking the individual bonds between the individual bonds. That is, the external load applied to the entire section of the sample is compensated by the resistance not of the entire cross section at the same time, but of individual bonds, individual fibers, separate

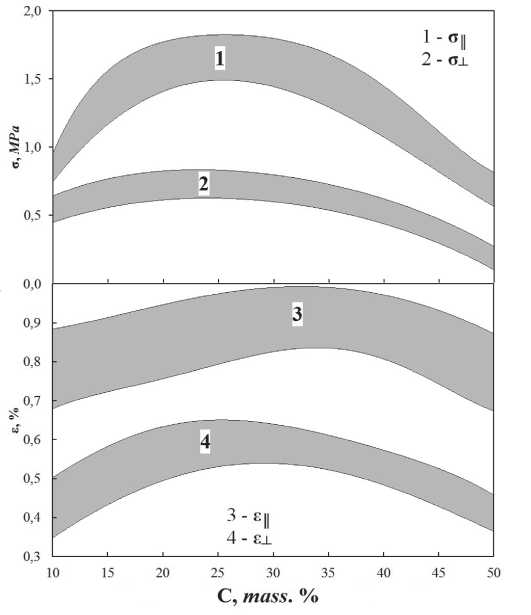
Fig. 3. Dependence of the ultimate strength and minimum elongation at tension (ρ = 0.19 g/cm3)

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

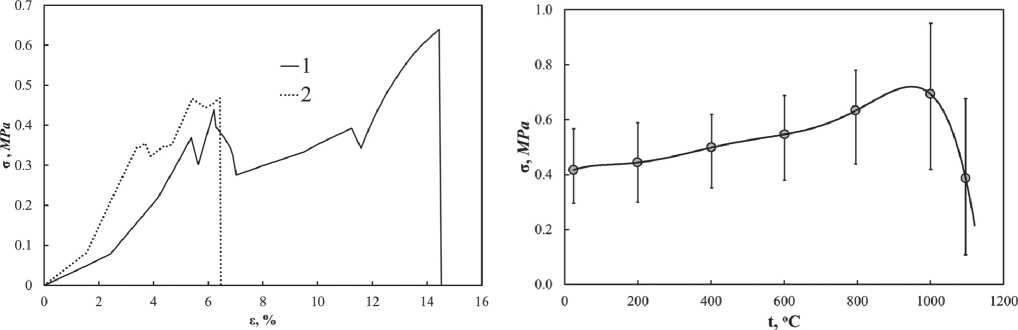
Fig. 4. Diagrams σ–ε when testing the material for tension.

1 – Test temperature of 800oC;

2 – Test temperature of 1000oC

Fig. 5. Dependence of FRCI tensile strength on test temperature

layers of material. And so, it continues until all fibers of communication are dragged down in a pattern.

Fig. 5 is a graph of the strength of the FRCI material versus the temperature of the tensile test [20]. It shows that as the test temperature rises, there is a tendency to increase the strength of the material. With increasing temperature, the reaction of welding fibers at the points of contact increases, and the number of such strong bonds increases. Besides, self-healing of the defects of the fibers themselves occurs, which also increases their strength properties.

When testing the material for compression, the deformation diagram had the form of Fig. 6. By the form of the diagram, it can be concluded that under the influence of stresses, the block of fibers is overloaded, they are destroyed – the load falls off in the diagram. Then the load continues to grow and the cycle repeats until destroyed. The selection of heat-shielding materials is usually performed according to their thermal conductivity.

Variable thermal conductivity is a function of parameters such as temperature, bulk density, porosity, pore size, radiation properties of the material, composition of the solid phase, composition of the gas phase, etc.

The dependence on the bulk mass passes, as we know, through a minimum [21]. Its relative value increases with increasing temperature. This is true for all kinds of materials, both cellular and fibrous.

Dependence of the thermal conductivity on the magnitude and type of pores with decreasing pore size also reduces the variable thermal conductivity. Thermophysical properties of materials are affected by the nature of scattering and absorption by particles within the structure of the material. Radiation properties of materials depend on the chemical and mineralogical composition, the structure of the material, on the nature of the contact of the particles, and their morphology. For example, a high SiO2 content has a positive effect on the decrease in thermal conductivity in SiO2–Al2O3 systems at elevated temperatures.

Thermophysical characteristics of reusable heatshielding materials developed within the framework of the “Space shuttle” program are presented in Table [7, 22].

With increasing thermal stresses, the safety of the heat-shielding material can be ensured by an appropriate coefficient of thermal expansion. In this respect, materials based on mullite can be subjected to much higher loads than materials based on SiO2.

The most critical parameter of heat-shielding material is thermal conductivity. The values of the thermal conductivity coefficients of FRCI thermal protection materials range from 0.2 to 1.5 W/m•deg. And with a decrease in fiber diameter, the coefficient of thermal conductivity decreases. Fibers of smaller diameter promote the formation of substantially smaller pores in the material, which leads to a decrease in convective and radiant heat transfer.

2.    Materials with a regular and quasiregular porous structure.

Materials with a regular or quasi-regular structure are the so-called cellular, cellular or «lattice» materials.

An example of such materials is a foam ceramic – a sintered material on a mineral basis with a foam-like structure. The structure of the material consists of air bubbles (or another gas), surrounded by thin shells, forming a kind of skeleton. Foam ceramic is usually obtained based on highly disperse mineral powders and liquid foams. Such foams are colloidal systems with a liquid

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

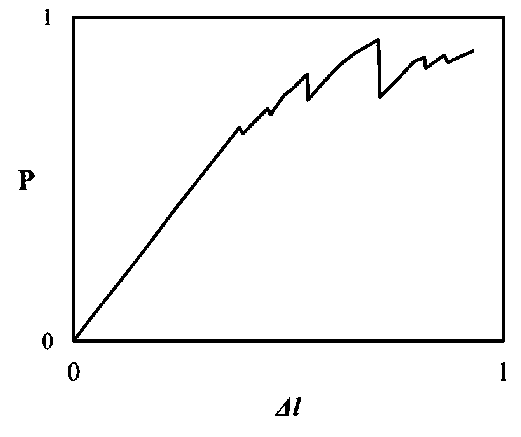
Fig. 6. Typical FRCI material deformation diagram for compression interface, the dispersion medium is a liquid, and the dispersed phase is a gas in the form of bubbles separated from each other by fluid films.

The structure of these materials is a lattice of a coherent network of racks. In the language of construction equipment, a lattice truss or a spatial frame means an array of racks articulated and rigidly connected, usually from one of the traditional building materials: wood, steel, or aluminum. Their purpose is to create a rigid, sturdy load-bearing structure, using as little material as possible, while ensuring its minimum weight. The word “lattice” is also used in other contexts: in the language of crystallography, for example, the lattice is a hypothetical grid of connected lines with three-dimensional translational symmetry. The intersections of lines determine atomic objects in a crystal; the elementary cell and the symmetry elements of the lattice characterize the class of crystals.

Here we deal with lattice, cellular or cellular materials. As engineering farms and frames, they consist of a bounded array of struts or plates, and, as in the crystal lattice, they are characterized by a typical cell with certain symmetry elements; some of which, but not all, have translational symmetry. But lattice materials differ from engineering grids in one important respect, namely on a scale. Elementary cells of lattice materials are measured in millimeters or micrometers, and this is what allows them to be considered both as a structure and as a material. On the one hand, they can be analyzed using classical methods of mechanics, just as any spatial frame is analyzed. On the other hand, it is necessary to think about the lattice not only as a set of connected racks, but also as a «material» in itself, with its own set of specific properties. This allows it to be directly compared with the same, but monolithic materials.

Historically, foams represent a certain subset of lattice-structured materials, and they were studied long before, but attention was focused on gratings of other types. Early studies assumed that the foam properties linearly depend on the relative density p/ρs (ie, the volume fraction of the solid in the material), but for most foams this is not the case. A clear understanding of their mechanical properties of foams began to appear after 1970, the ambassadors of the appearance from the works [23, 24]. Since then, a complete understanding of the mechanical, thermal and electrical properties of foams has been achieved. These ideas have been successfully applied to ceramic foam [25–34]. Recent achievements in this field were reflected in the generalized monograph [35].

Table

Thermophysical characteristics of heat-resistant materials of repeated use of FRCI type [22]

Characteristics	Thermal protection material
	based on SiO2	based on mullite
Coefficient of thermal expansion, K –1 – heat-protection tiles – protective coatings	0.5•10–6 0.7•10–6	5.0•10–6 5.0•10–6
Specific mass heat capacity cal/g•deg	0.24	0.25
Coefficient of total reflection of the protective coating	0.9	0.7÷0.85
Temperature limit at which zero strength is achieved, oC – heat-protection tiles – protective coatings	1260 1100	1260 750÷1240

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

One of the key facts is that deformations in most foams, whether with open or closed pores, flexural-dominant – a term that is explained in more detail below. The consequence of this is that their rigidity and strength (at a given relative density) falls well below the levels that would be expected for structures with a predominance of tensile stresses, of which the fully triangulated lattices are a typical representative. To give an idea of what is the difference, let us compare the grids with a low level of connectivity, a typical example of which are foams, with a relative density of 0.1 (this means that the solid walls of the cells occupy 10% of the volume).

Such structures are less rigid than structures with a predominance of tensile stresses, which are triangulated lattices, with the same relative density. In this section, we consider the essential features of both structures, with both the prevalence of bending stresses and tensile stresses, using dimensional methods to arrive at simple approximate similarity laws for mechanical, thermal, and electrical properties.

Fig. 7 shows an image of ceramic foam with open pores. It represents one of the classes of lattice-structured materials. It consists of pillars connected in knots. For this class is characteristic low connectivity of nodes (the average number of racks that connect in one node).

Fig. 8 shows the idealization of a unit cell of a similar structure. It consists of solid bridges surrounding an empty space containing gas or liquid.

The lattice-structured materials are often called cellular solid substances. They are characterized by relative density, which (for t <<  L ) for the structure shown here has the form:

p_o   7 /t\²   /t\³    /t\²

— = - -  — - oc - ps   4\LJ   \LJ    XL;

Where p_o is the density of the foam, ρ_s is the density of the solid from which it was made, L is the cell size, and t is the thickness of the cell edges. The role of the cubic term in expression (1) becomes significant for t / L > 0.15. Yes, and this model itself has strict limitations, and has a physical meaning only in the range t / L < 0.5. That is, when the thickness of the bridge is less than one-half the length of the cubic part of the cell. The dependence of the relative density p_o/ρ_s on the ratio t / L is shown in Fig. 9. For comparison, the graph of the quadratic term of equation (1) is given in this figure (curve 2).

Materials with a lattice structure in which there is a low connectivity of the posts, as depicted in Fig. 7 and 8, have low rigidity, since the configuration of the edges of their cells allows them to bend. There may be other configurations in which the edges of the cell are made in such a way that, instead of bending, a stretching is observed in their structure. This assumption leads to the idea of lattice constructions built from micro-truss.

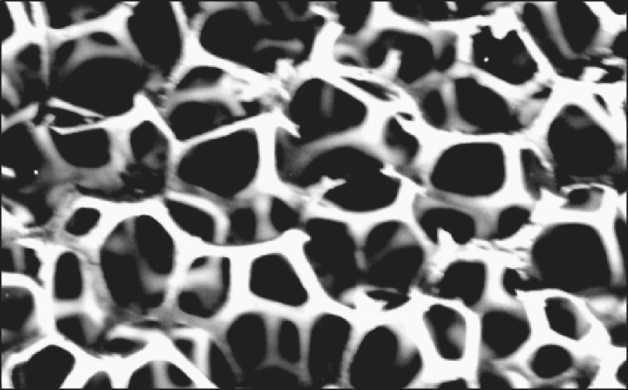
Fig. 7. An enlarged image of a typical cell structure represented in Figure 2. The topology of the cells is constructed in such a way that the cellular edges are bent, in the presence of an external load on the structure. Even when the cells are closed, bending deformations are predominantly observed, this is because the thin sides of the cells bend easily enough

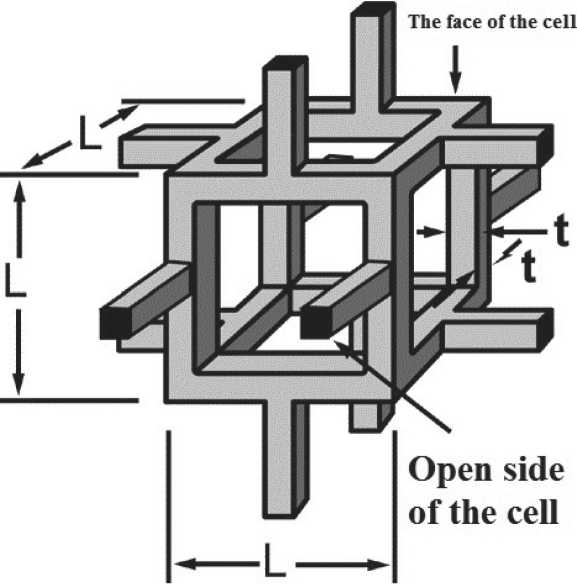
Fig. 8. Idealized cells in open-cell foam

To understand this, it is necessary to use Maxwell’s stability criterion, which is a simple but deeply fundamental rule [36]. As follows from the laws of mechanics, in order to determine the stability of a system of beams and a truss, they must be statically as well as kinematically definable at least in two dimensions, i.e. this means: to be rigid and not folding, being loaded.

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

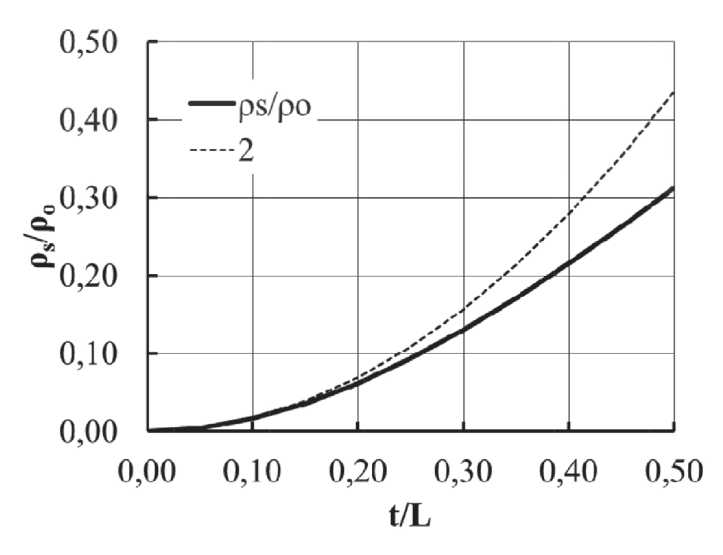
Fig. 9. Dependence of the relative density p o /ρ s on the ratio t / L and the magnitude of the quadratic term of Eq. (1) (curve 2)

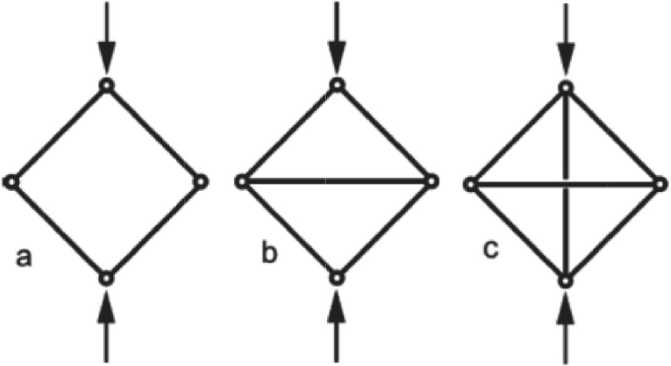
Fig. 10. a) Articulated frame, which folds under load, is a mechanism. If its connections are rigid, they are welded together, bends of the pillars (as in Fig. 11) occur – it becomes a flexural-dominant structure.

• b)    A rigid triangulated frame in the case of loading, since the transverse strut experiences stress – it is a stretched-dominant structure.

Thus, for a truss with nodal joins (i.e. which are hinged at their nodes) consisting of b columns and j nodes without friction, such as those shown in Fig. 10, is the expression:

M = b –2 j +3 = 0.

• c)    A frame with an additional restriction; if the horizontal band is shortened, then in the vertical there is a voltage, even if there are no external loads (gives the state of internal voltage)

  For the case of three dimensions, the equivalent equation is:

  M = b –3 j +6 = 0. (3)

  If M < 0, as shown in Fig. 10a, the frame is a mechanism that has one or more degrees of freedom in those directions that allow appropriate displacements, while it does not have stiffness or strength. If its nodes are locked (as we are considering lattice constructions), the frame bars bend when the structure is loaded, as shown in Fig. 11.

  If M = 0, as shown in Fig. 10b, the frame ceases to be a mechanism. If it is loaded, its elements experience tensile or compressive stresses (such a situation is observed even in the case of articulation), and it becomes a structure with a predominance of tensile stresses. Blocking junctions in this case changes little, because the lace structures are much more rigid when stretched than when bending. Here the basic principle operates: the structural efficiency of structures with a predominance of tensile stresses is high; in turn, for flexural-dominant structures it is low.

  To understand the mechanical behavior of such structures, an additional concept of the internal stress state introduced in Fig. 10c was introduced in [35]. This is a structure with M > 0. If the vertical pillar is shortened, it pulls the other pillars into a compression state, which is balanced by the tension that it creates.

  
  
  

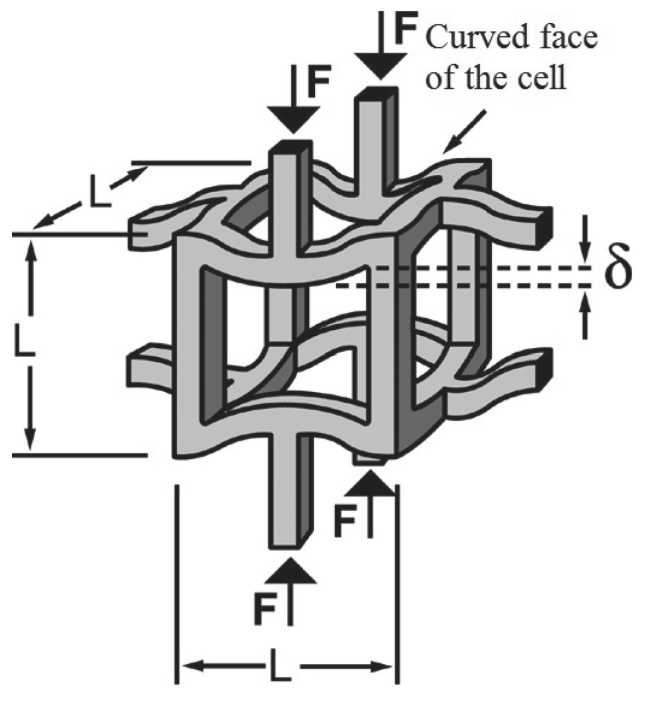
  Fig. 11. Schematic behavior of a loaded structure with low connectivity. There is a bending of the cell edge, thus providing a low modulus of elasticity. δ is the strain value

  
  

  INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

  

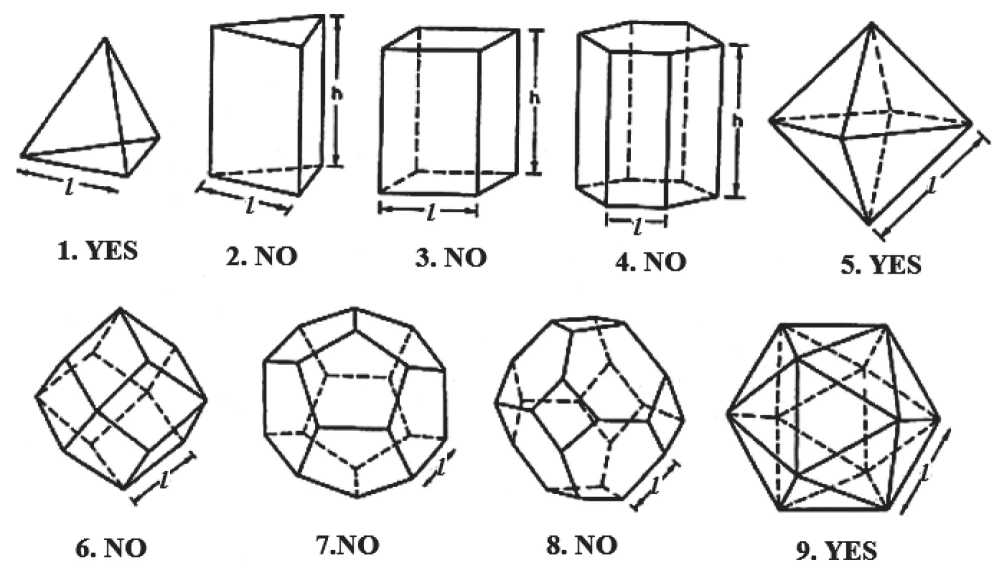
  Fig. 12. Polyhedral cells. Cells that, when filling a space, have M < 0 (2–4, 6–8), are structures with a predominance of bending stresses [35]

  
  

The racks in this structure are in a stressed state, even if there are no external loads on the entire structure. The criteria for equations (2) and (3) are necessary conditions for the rigidity of the construction, but are not generally enough conditions, since they do not consider the possibilities of states of internal stress and the state of the mechanism. A generalization of Maxwell’s rule in three dimensions is given in [37]:

M = b –3 j +6 = s – m , (4)

where s and m are the number of states of internal stresses and mechanisms, respectively. Each of them can be determined by finding the rank of the equilibrium matrix describing the frame in the complete structural analysis [38]. Simply – a rigid frame (for a lattice that is statically and cinematically determinable) has s = m = 0. The nature of Maxwell’s rule as a necessary but not enough condition is clear from an analysis of equation (4). Zero on the left side means only that the number of mechanisms and states of internal stress are equal, and not that each of them is zero.

The Maxwell criterion gives an idea of the design of lattice materials and shows why foams almost always produce materials with a predominance of bending stresses [39–41]. Examples of some idealized cell forms are shown in Fig. 12. Isolated cells that satisfy the Maxwell criterion and are rigid are labeled «YES», while «NO» means that the Maxwell condition is not satisfied, and that this cell is a mechanism. In this case, as a rule, it is assumed that a suitable model for the cell in the foam corresponds to approximately filling the volume of material with cells of a given spatial shape. Nevertheless, the structures obtained when filling the space with forms are indicated by the numerals 2, 3, 4, 6 and 8, are not rigid.

In addition, none of the cells represented in the form of polyhedra filling the space have M ≥ 0. Among the forms of cells filling the space, there are combinations for which M = 0; for example, tetrahedron and octahedron, which in combination with each other, during space filling, and allow to form a rigid base.

The Maxwell criterion provides an analytical approach to the design of lattices with the predominance of tensile forces in their structure.

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

ВВЕДЕНИЕ

Д анная статья является продолжением серии наших статей, посвященных получению пористых композиционных наноматериалов. В предыдущей работе [1] был проведен анализ основных типов пористых термостойких материалов. Проведено сравнение различных химических веществ, обладающих наибольшей термостабильностью и огнеупорностью, что позволило выбрать объекты, в наибольшей степени подходящие для создания соответствующих композиционных материалов. В работах [2, 3] проведен анализ структуры пор в твердых пористых твердых телах. В этой работе мы постарались осветить свойства основных пористых термостойких материалов, выпускаемых промышленно. Первый обзор, посвященный подлобным материалам, был выпущен уже давно и был посвящен только пористой конструкционной керамике [4]. В данной работе мы рассмотрели не только конструкционную керамику, но и функциональные пористые материалы.

Передовая пористая керамика широко используется для решения целого ряда экологических, биологических и технических проблем, стоящих перед современной промышленной технологией. Керамические материалы обладают многими преимуществами по сравнению с другими материалами, такими как полимеры или металлы. Они обладают такими уникальными свойствами как твердость, износостойкость, химическая инертность, стойкость к термическому удару и коррозии. Низкая плотность таких материалов является качеством, которое необходимо для многих практических применений.

К настоящему времени разработано множество различных типов пористых огнеупорных материалов. Выпускаемые промышленностью теплозащитные материалы [4, 6–8] классифицируются по объемной массе (кг/м3) на марки (15÷700). Коэффициент теплопроводности для высокоэффективных материалов находится в пределах 0,01÷0,15 Вт/м•К, для низкоэффективных до 0,25 Вт/м•К.

Большую группу среди них занимает пенообразные материалы, получаемые за счет введения в исходную шихту порообразователей [9–11] или выжигания одного из компонентов шихты [8, 12, 13]. Все эти материалы отличаются достаточно высокой плотностью от 0,5 до 1,5 г/см3 и соответственно низкой пористостью и высокой теплопроводностью. Известен широкий класс материалов, получаемый путем сжигания сферичных порошков огнеупорных оксидов, в котором пористость достигается путем регулирования характера контактов и плотностью упаковки частиц в материале. Однако таким образом получаются плотные композиции с удельным весом 1÷2 г/см3 [5]. При этом получение сферических по- рошков является сложной проблемой, требующей применения низкотемпературной плазмы.

Более высокими показателями, по сравнению с данными материалами, обладают материалы на основе различных неорганических микросфер и минеральных волокон. Для композиций на основе микросфер характерно наличие достаточно высокой прочности, до 100 МПа при плотности, равной 0,35–0,40 г/см3 [7, 14, 15]. Однако сложной является методика получения пустотелых микросфер, требующая использования процесса раздува расплава формируемого оксида в строго определенных гидродинамических параметрах.

Наиболее перспективными в плане получения являются волокнистые материалы, так как на их основе создаются высокопористые композиции. Известен способ изготовления огнеупорной теплоизоляции из волокон, которые обрабатывают водными растворами солей хрома Сr(ОН)SO4 и CrСl3 с использованием осадителей NaOH и КОН [16]. К недостаткам этого материала следует отнести наличие в его структуре ионов щелочных металлов, приводящих к значительному снижению термостойкости в результате образования легкоплавких эвтектик.

Например, на ряде огнеупорных производств в РФ выпускаются такие виды легковесных теплоизоляционных огнеупорных изделий, как ШЛ-1,3; ШЛ-1,0; ШЛ-0,4. Кроме этих изделий производится огнеупорный теплоизоляционный стекловолокнистый муллито-кремнеземистый материал марки МКРР-130 [17]. На основе его выпускаются муллито-кремнеземистые плиты на органическом связующем марки МКРП-340 и марки МКР1М-500 на глинистом связующем [17]. Но у этих материалов есть недостаток – наличие органического связующего приводит к значительному снижению их термостойкости и появлению большого объема продуктов разложения органического вещества при эксплуатации.

Наибольшие успехи в области получения легковесных огнеупорных материалов были достигнуты в США в результате разработки производства и летных испытаний системы теплозащиты многоразового воздушно-космического аппарата «Space shuttle». Фирмой Rockwell International были изготовлены плитки из керамического волокна двух типов LI-900 с плотностью 0,144 г/см3 [18]. Фирмой Lockheed для космических кораблей «Аполлон» был разработан теплозащитный материал LI-1500 с плотностью 0,24 г/см3. В дальнейшем, в результате исследований по улучшению характеристик материала LI-1500 основное внимание уделялось химическому составу волокна, что привело к созданию волокон диоксида кремния высокой степени чистоты и повышению термостойкости материала LI-1500. Благодаря новым волокнам и усовершенствованным методам обра-

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

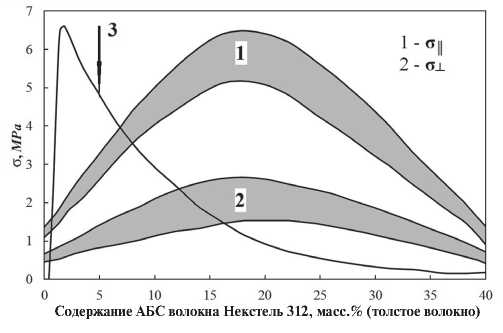
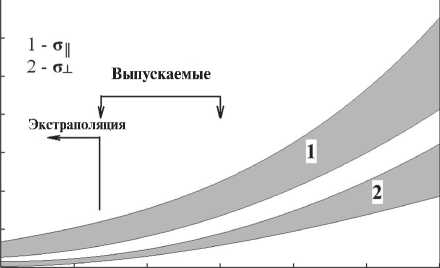
Рис. 1. Зависимость предела прочности на изгиб FRCI (ρ = 0,32 г/см³):

3 – содержание кристобалита (%)

50        100        150        200        250        300        350

ρ, кг/м³

Рис. 2. Зависимость предела прочности FRCI-20 на разрыв от плотности

ботки, изменившим их ориентацию, размещение связующего компонента в структуре композита, был создан новый теплозащитный материал LI-900.

На основе алюмоборсиликатного волокна Нек-стель 312 и микрокварца научно-исследовательским центром им. Эймса был разработан новый материал FRCI с целым рядом новых свойств [19].

1.    Физико-химические характеристики пористых огнеупорных материалов

Наиболее подробно физико-химические характеристики высокопористых огнеупорных материалов изучены для материала FRCI, разработанного фирмой «Lockheed» и лабораторией им. Эймса [19]. FRCI построен из двух типов волокон. Волокно первого типа – алюмоборсиликатное Некстель 312 фирмы «Manning» диаметром 11 мкм и длиной 0,31 см. Волокно второго типа – микрокварц фирмы «Johns Manville» диаметром 1÷3 мкм. Относительная прочность материала FRCI, характеризуемая пределом прочности при изгибе в направлениях параллельном или перпендикулярном ориентации волокон представлена на рис 9. Максимальная прочность достигается при 20% содержании алюмоборсиликатного волокна Некстель 312. На рис. 1 показана также устойчивость морфологии структуры полученного материала, характеризуемая содержанием кристобалита после выдержки при 1370оС в течение 4 часов.

На рис. 2 представлена зависимость предела прочности при растяжении от величины плотности для материала FRCI-20.

При плотности 0,19 г/см3 предел прочности при растяжении в направлении наибольшей прочности или ориентации волокон составляет 18,5÷17,6 кг/см2

и при растяжении в направлении наименьшей прочности или перпендикулярно ориентации волокон 5,0÷9,8 кг/см2 (см. рис. 3). Удлинение при разрушении составляет соответственно 0,38÷0,53% при растяжении параллельно ориентации волокон

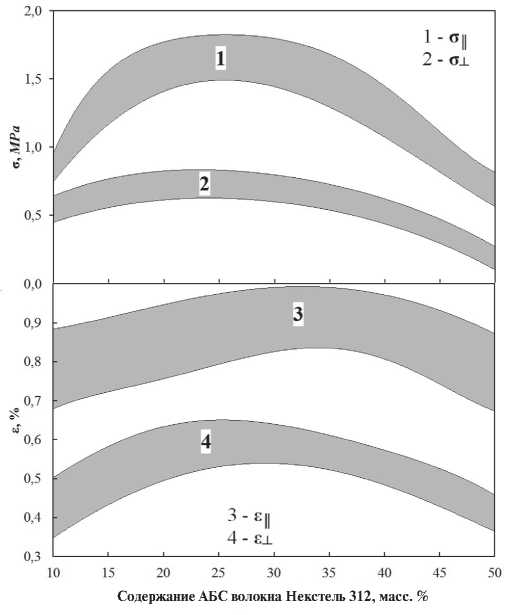
Рис. 3. Зависимость предела прочности и минимального относительного удлинения при растяжении (ρ = 0,19 г/см³)

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

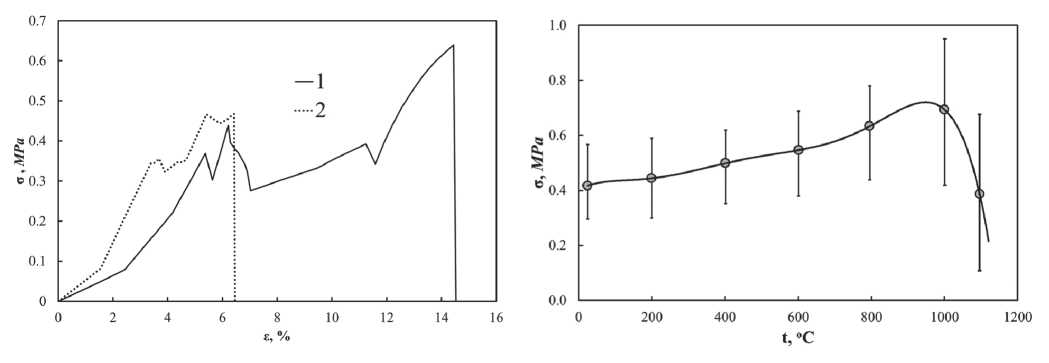
Рис. 5. Зависимость прочности на разрыв FRCI от температуры испытаний

Рис. 4. Диаграммы σ–ε при испытании материала на разрыв:

1 – температура испытаний 800оС;

2 – температура испытаний 1000оС и 0,7÷0,9% при растяжении перпендикулярно ориентации волокон (рис. 3) [18].

Материал FRCI-20 был исследован в Институте проблем прочности [20]. Были получены диаграммы зависимости напряжения от деформации, прочностные и упругие характеристики материала в широком температурном интервале от 20 до 1000оС при различных видах нагружения. На рис. 4 представлены примеры диаграмм нагружения.

Из этих примеров видно, что при нагружении образцов в большей или меньшей степени наблюдаются срывы нагрузок с дальнейшим ее возрастанием. Видимо, при испытании разрушение материала происходит не одновременно, а последовательно, путем разрыва отдельных связей между отдельными связями. То есть внешняя нагрузка, прикладываемая ко всему сечению образца, компенсируется сопротивлением не всего сечения одновременно, а отдельных связей, отдельных волокон, отдельным слоев материала. И так продолжается до тех пор, пока не разрушатся все волокна связи волоком в образце.

На рис. 5 приведена диаграмма зависимости прочности материала FRCI от температуры испытаний на разрыв [20]. Она показывает, что при повышении температуры испытаний наблюдается тенденция к росту прочности материала. С повышением температуры усиливается реакция сваривания волокон в местах их контакта, усиливается количество таких прочных связей. И, кроме этого, происходит самозалечивание дефектов самих волокон, что также увеличивает их прочностные свойства.

При испытании материала на сжатие диаграмма деформирования имела вид рис. 6. По виду диаграммы можно заключить, что под действием на- пряжений происходит перегрузка блока волокон, они разрушаются – на диаграмме происходит спад нагрузки. Затем нагрузка продолжает расти, и цикл повторяется до полного разрушения. Подбор теплозащитных материалов производится обычно по значениям их теплопроводности.

Изменяемая теплопроводность является функцией таких параметров, как температура, объемная масса, пористость, размер пор, радиационные свойства материала, состав твердой фазы, состав газовой фазы и т.д. Зависимость от объемной массы проходит, как известно, через минимум [21]. Относительная

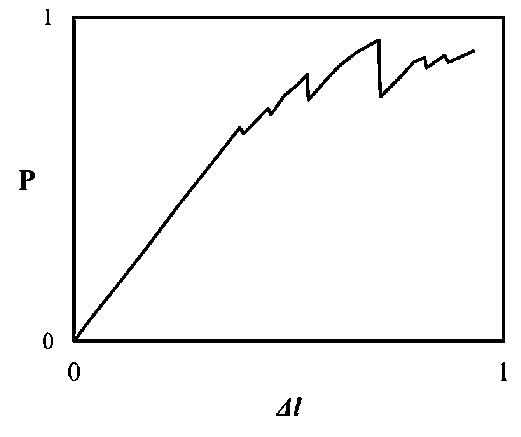
Рис. 6. Типичная диаграмма деформирования материала FRCI при сжатии

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

Таблица

Теплофизические характеристики теплозащитных материалов многократного применения типа FRCI [22]

Характеристики Теплозащитный материал на основе SiO2 на основе муллита Коэффициент теплового расширения, K–1 – теплозащитные плитки – защитные покрытия 0,5•10–6 0,7•10–6 5,0•10–6 5,0•10–6 Удельная массовая теплоемкость кал/г•град 0,24 0,25 Коэффициент полного отражения защитного покрытия 0,9 0.7÷0,85 Температурный предел, при котором достигается нулевая прочность, oC – теплозащитная плитка – защитное покрытие 1260 1100 1260 750÷1240 ее величина увеличивается с ростом температуры. Это справедливо для любых видов материалов как ячеистых, так и волокнистых.

Зависимость теплопроводности от величины и вида пор с уменьшением величины пор понижается, также изменяемая теплопроводность. На теплофизические свойства материалов оказывает влияние характер рассеивания и поглощения частицами, находящимися внутри структуры материала. Радиационные свойства материалов зависят от химического и минералогического состава, строения материала, от характера контакта частиц, их морфологии. Например, положительное влияние на снижение теплопроводности в системах SiO2–Al2O3 при повышенных температурах оказывает большое содержание SiO2. Теплофизические характеристики теплозащитных материалов многократного применения, разработанные в рамках программы «Space shuttle», представлены в табл. [7, 22].

При возрастании тепловых напряжений сохранность теплозащитного материала может быть обеспечена за счет соответствующего коэффициента теплового расширения. В этом плане материалы на основе муллитов могут подвергаться значительно более высоким нагрузкам, чем материалы на основе SiO2.

Наиболее критичным параметром теплозащитного материала является теплопроводность. Значение коэффициентов теплопроводности материалов теплозащиты FRCI находятся в пределах от 0,2 до 1,5 Вт/м•град. Причем с уменьшением диаметра волокна коэффициент теплопроводности снижается. Волокна меньшего диаметра способствуют образованию в материале существенно меньших пор, что приводит к уменьшению конвективного и лучистого теплообмена.

2.    Материалы с регулярной и квазирегулярной пористой структурой

К материалам с регулярной или квазирегуляр-ной поровой структурой относятся так называемые ячеистые, клеточные или «решеточные» материалы.

Примером таких материалов является пеноке-рамика – спеченный материал на минеральной основе с пеноячеистой структурой. Структура материала состоит из пузырьков воздуха (или другого газа), окруженных тонкими оболочками, образующими своеобразный каркас. Пенокерамика обычно получается на основе высокодисперсных минеральных порошков и жидких пен. Такие пены представляют собой коллоидные системы с жидкой поверхностью раздела, дисперсионной средой является жидкость, а дисперсной фазой – газ в виде пузырьков, отделенных друг от друга пленками жидкости.

Структура этих материалов представляет собой решетку из связной сети стоек. На языке строительной техники решеточная ферма или пространственная рама означает массив стоек, сочлененных и жестко связанных между собой, как правило, из одного из традиционных строительных материалов: дерева, стали или алюминия. Их назначение заключается в создании жесткой, прочной несущей конструкции, используя по возможности как можно меньше материала и обеспечивая при этом ее минимальный вес. Слово «решеточные» используется и в других контекстах: на языке кристаллографии, например, решетка – гипотетическая сетка связных линий с трехмерной трансляционной симметрией. Пересечения линий определяют атомные объекты в кристалле; элементарная ячей-

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ ка и элементы симметрии решетки характеризуют класс кристаллов.

Здесь мы имеем дело с решеточными, ячеистыми или клеточными материалами. Как инженерные фермы и рамы, они состоят из связанного массива распорок или пластин, и, как в кристаллической решетке, они характеризуются типичной ячейкой с определенными элементами симметрии; некоторые из которых, но не все, имеют трансляционную симметрию. Но решеточные материалы отличаются от инженерных решеток в одном важном отношении, а именно в масштабе. Элементарные ячейки решетчатых материалов измеряются в миллиметрах или микрометрах, и именно это позволяет им рассматриваться как в качестве структуры, так и в качестве материала. С одной стороны, они могут быть проанализированы с помощью классических методов механики так же, как анализируется любая пространственная рама. Но, с другой стороны, необходимо думать о решетке не только как о наборе связанных стоек, но и как о «материале» самом по себе, со своим набором конкретных свойств. Это позволяет непосредственно сравнивать его с такими же, но уже монолитными материалами.

Исторически сложилось так, что пены представляют собой определенное подмножество решеточно-структурированных материалов, и они были изучены задолго до этого, однако внимание было сосредоточено на решетках других типов. Ранние исследования предполагали, что свойства пены линейно зависят от относительной плотности p ⁄ρs (т.е. объемной доли твердого вещества, в материале), но для большинства пен это не так. Четкое понимание их механических свойств пен стало появляться после 1970 года, после появления работ [23, 24]. С тех пор было достигнуто достаточно полное понимание механических, тепловых и электрических свойств пен. Эти идеи были с успехом применены для керамической пены [25–34]. Последние достижения в этой области были отражены в обобщенной монографии [35].

Одним из ключевых фактов является то, что деформации в большинстве пен, будь то с открытыми или закрытыми порами, изгибно-доминирующие – термин, который объясняется более подробно ниже. Следствием этого является то, что их жесткость и прочность (при заданной относительной плотности) падает значительно ниже уровней, которые следовало бы ожидать для структур с преобладанием растягивающих напряжений, типичным представителем которых являются полностью триангулированные решетки. Чтобы дать представление о том, в чем разница, сравним решетки с низким уровнем связности, типичным примером которой являются пены, с относительной плотно-

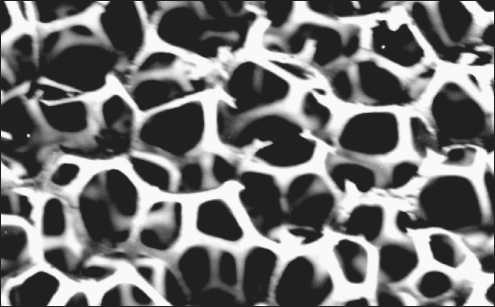
Рис. 7. Увеличенное изображение типичной клеточной структуры. Топология ячеек построена таким образом, что края ячеек изгибаются при наличии внешней нагрузки на конструкцию. Даже когда ячейки закрыты, преимущественно наблюдаются деформации изгиба, потому что тонкие стороны ячеек изгибаются достаточно легко стью 0,1 (это означает, что твердые стенки ячеек занимают 10% от объема). Такие структуры являются менее жесткими, чем структуры с преобладанием растягивающих напряжений, которыми являются триангулированные решетки, с той же относительной плотностью.

В этом разделе мы рассмотрим существенные черты обеих структур, как с преобладанием напряжений изгиба, так и напряжений растяжения, используя размерные методы, чтобы прийти к простым приближенным законам подобия для механических, тепловых и электрических свойств.

На рис. 7 представлено изображение керамической пены с открытыми порами. Оно представляет один из классов решеточно-структурированных материалов. Он состоит из стоек, соединенных в узлах. Для этого класса является характерной низкая связность узлов (среднее количество стоек, которые соединяются в одном узле). Топология ячеек построена так, что заставляет изгибаться клеточные края при наличии внешней нагрузки на структуру. Даже тогда, когда ячейки закрыты, преимущественно наблюдаются деформации изгиба, это связано с тем, что тонкие грани ячеек гнутся достаточно легко.

На рис. 8 представлена идеализация элементарной ячейки подобной структуры. Она состоит из твердых перемычек, окружающих пустое пространство, содержащее газ или жидкость.

Решеточно-структурированные материалы часто называются клеточными твердыми веществами. Они характеризуются относительной плотностью, которая (при t <<  L ) для структуры, показанной здесь, имеет вид:

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ po   7 /t\2   /t\3   /t\2

— = - -  — - oc - ps   4\LJ   \LJ    XL;

где P_o представляет собой плотность пены, ρ_s – плотность твердого вещества, из которого она сделана, L – размер ячейки и t – толщина краев ячейки. Роль кубического члена в выражении (1) становится существенно при t / L > 0,15. Да и сама эта модель имеет жесткие ограничения и несет физический смысл только в диапазоне t / L < 0,5. То есть, когда толщина перемычки меньше половины длины грани кубической части ячейки. Зависимость относительной плотности P_o/ρ_s от отношения t / L представлена на рис. 9. Для сравнения на этом рис. приведен график (кривая 2) квадратичного члена уравнения (1).

Материалы с решетчатой структурой, в которой имеется низкая связность стоек, как это изображено на рис. 7 и 8, имеют низкую жесткость, поскольку конфигурация краев их ячейки позволяет им изгибаться. Возможно наличие других конфигураций, в которых края ячейки выполнены таким образом, чтобы вместо изгиба в их структуре наблюдалось растяжение. Это предположение приводит к идее решетчатых конструкций, построенных из микроферм.

Чтобы понять это, необходимо использовать критерий устойчивости Максвелла, который представляет собой простое, но глубоко фундаментальное правило [36]. Как следует из законов механики, для определения устойчивости системы балок и фермы они должны быть как статически, так и кинемати-

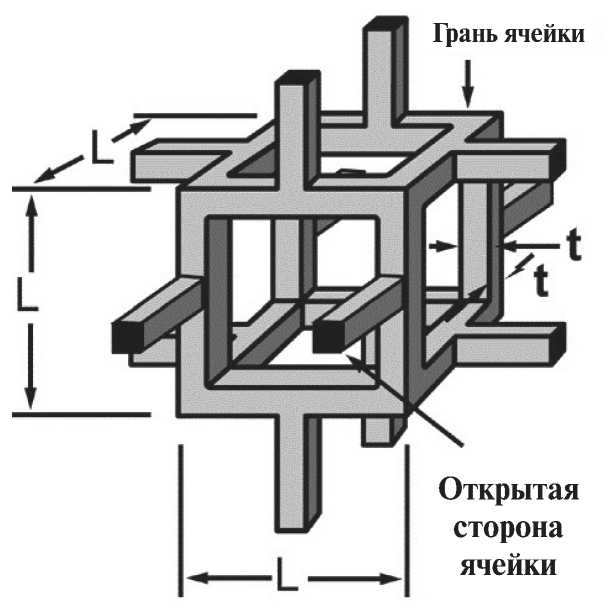
Рис. 8. Идеализированные ячейки в пене с открытыми порами

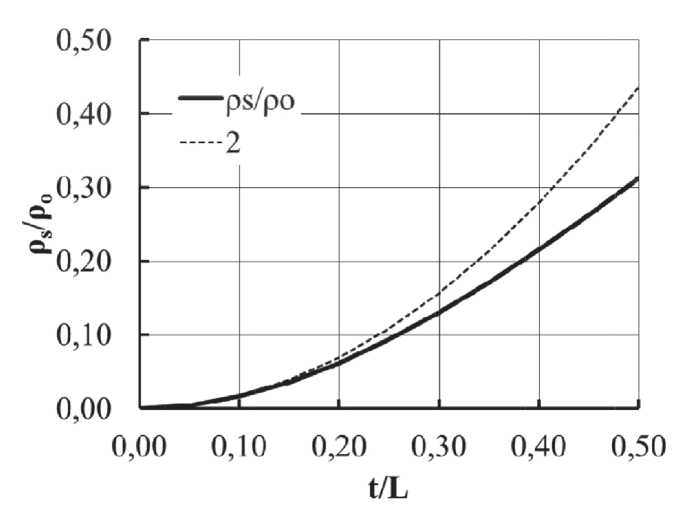
Рис. 9. Зависимость относительной плотности P o /ρ s от отношения t / L и величина квадратичного члена уравнения (1) (кривая 2)

чески определимыми хотя бы в двух измерениях, т.е. это означает быть жесткой и не складывающейся, будучи нагруженной. Таким условием, для фермы с узловыми соединениями (т.е. которые закреплены шарнирно в своих узлах), состоящей из b стоек и j узлов без трения, таких как те, что представлены на рис. 10, является выражение:

M = b –2 j +3 = 0. (2)

Для случая трех измерений эквивалентное уравнение представляет собой:

M = b –3 j +6 = 0. (3)

Если M < 0, как изображено на рис. 10а, рама представляет собой механизм, который имеет одну или несколько степеней свободы в тех направлениях, которые позволяют соответствующие смещения, при этом она не имеет жесткости или прочности. Если ее узлы заблокированы (поскольку мы рассматриваем решетчатые конструкции), прутья рамы изгибаются, когда структура загружается, как показано на рис. 11.

Если М = 0, как показано на рис. 10b, рамка перестает быть механизмом. Если он будет нагружен, его элементы испытывают напряжения, растяжения или сжатия (такая ситуация наблюдается даже в случае шарнирного сочленения), и она становится структурой с преобладанием растягивающих напряжений. Блокировка сочленений в данном случае мало что меняет, потому что ажурные структуры гораздо жестче при растяжении, чем при изгибе. Здесь действует основной принцип: структурная эффективность структур с преобладанием растягивающих напряже-

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

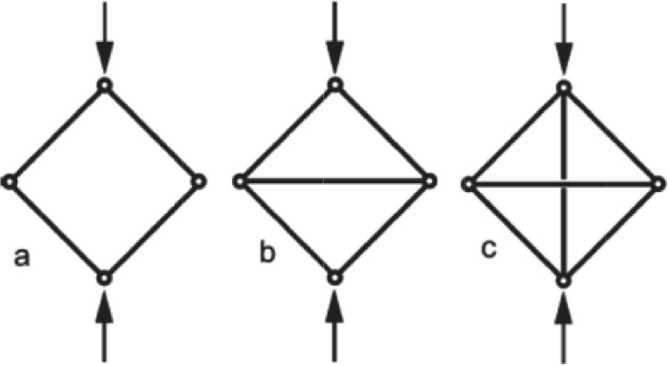
Рис. 10. Варианты ферм с узловыми соединениями, моделирующих строение ячеистых материалов: а) Шарнирно-сочлененная рамка, которая складывается при нагрузке, представляет собой механизм. Если его соединения жесткие, свариваются вместе, происходит изгиб стоек (как на рис. 11) – она становится изгибно-доминирующей структурой; b) Жесткая триангулированная рамка в случае нагружения, так как поперечная распорка испытывает напряжение, – это растяженно-доминирую-щая структура;

c) Рамка с дополнительным ограничением; если горизонтальная полоса укорачивается, то в вертикальной возникает напряжение, даже если отсутствуют какие-либо внешние нагрузки (дает состояние внутреннего напряжения)

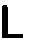
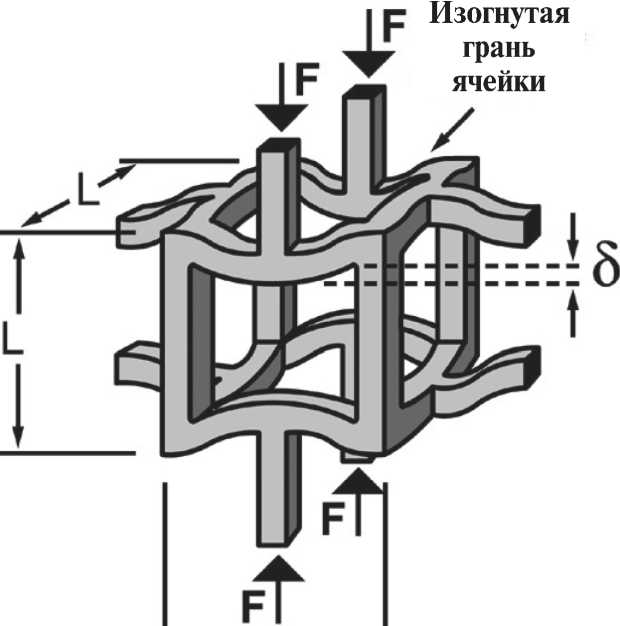
Рис. 11. Схематическое поведение нагруженной структуры с низкой связностью. Наблюдается изгиб края ячейки, обеспечивая, таким образом, низкий модуль упругости. δ – величина деформации ний высока; в свою очередь для изгибно-доминиру-ющих структур она является низкой.

Для понимания механического поведения подобных структур в работе [35] введена дополнительная концепция внутреннего напряженного состояния, представленная на рис. 10c. Это структура с М > 0. Если вертикальная стойка сокращается, она тянет другие стойки в состояние сжатия, которое уравновешивается натяжением, которое в ней возникает.

Стойки в этой структуре находятся в напряженном состоянии, даже если нет никаких внешних нагрузок на всю конструкцию. Критерии уравнений (2) и (3) являются необходимыми условиями для жесткости конструкции, но не являются в целом достаточными условиями, так как они не учитывают возможности состояний внутреннего напряжения и состояния механизма. Обобщение правило Максвелла в трех измерениях дается в работе [37]:

M = b –3 j +6 = s – m , (4)

где s и m – число состояний внутренних напряжений и механизмов, соответственно. Каждое из них может быть определено путем нахождения ранга равновесной матрицы, описывающей рамку в полном структурном анализе [37]. Просто жесткая рамка (для решетки, которая является статически и кинематически определимой) имеет s = m = 0. Характер правила Максвелла как необходимого, но недостаточного условия понятен из анализа уравнения (4). Нуль с левой стороны означает только то, что количество механизмов и состояний внутреннего напряжения равны, а не то, что каждый из них равен нулю.

Критерий Максвелла дает представление о дизайне решетчатых материалов и показывает, почему пены почти всегда дают материалы с преобладанием напряжений изгиба [39–41]. Примеры некоторых идеализированных форм ячейки показаны на рис. 12.

Изолированные клетки, которые удовлетворяют критерию Максвелла и являются жесткими, помечены «YES», в то время как «NO» означает, что условие Максвелл не выполняется и что данная ячейка является механизмом. При этом, как правило, предполагается, что подходящая модель для ячейки в пене соответствует приблизительному заполнению объема материала ячейками данной пространственной формы. Тем не менее, структуры, получаемые при заполнении пространства формами, обозначены цифрами 2, 3, 4, 6 и 8, не являются жесткими.

Кроме того, ни одна из представленных ячеек в форме многогранников, заполняющих пространство, не имеет М ≥ 0. Среди форм ячеек, заполняющих пространство, существуют такие комбинации, у которых М = 0; например, тетраэдр и октаэдр, кото-

INTERNATIONAL EXPERIENCE • МЕЖДУНАРОДНЫЙ ОПЫТ

Рис. 12. Полиэдрические ячейки. Ячейки, которые при заполнении пространства имеют М < 0 (2–4, 6–8), представляют собой структуры с преобладанием напряжений изгиба [35]

рые находятся в комбинации друг с другом во время заполнения пространства и позволяют сформировать жесткую основу.

Критерий Максвелла дает аналитический подход для проектирования решеток с преобладанием растягивающих усилий в их структуре и, соответственно, к получению более прочных и легких материалов. Продуктивность такого подхода полностью реализовалась при создании материалов с опаловой структурой, особенно для обратных опалов. В структуре этих материалов прекрасно реализуются структуры с критерием Максвелла М < 0.