Свойства структуры дисперсно-наполненных металлополимерных композитов

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2018PNRPU MECHANICS BULLETIN

Нефтепромысловое оборудование (НПО) эксплуатируется в тяжелых условиях, характеризующихся значительными динамическими нагрузками, интенсивностью абразивного изнашивания и коррозией материала в агрессивных средах эксплуатации. Указанные обстоятельства приводят к резкому падению ресурса НПО, увеличению числа ремонтных работ и простоев, увеличению межремонтного периода и, следовательно, повышению себестоимости добываемой продукции.

В настоящее время существует ряд технических, технологических и материаловедческих решений, позволяющих увеличить ресурс НПО, среди которых особое место занимают нанотехнологии и использование композитных материалов [1–4].

В последние несколько десятилетий получено достаточно много классов полимерных нанокомпозитов с различными механизмами упрочнения, которые объединяет реализация этих механизмов путем введения в полимерную матрицу высокодисперсных частиц нанометровых размеров. Одна из основных особенностей таких частиц – резкое увеличение площади контакта полимер–наполнитель по сравнению с обычно используемыми наполнителями микрометровых размеров, что обусловливает максимальный эффект упрочнения при малых содержаниях наполнителя.

Переход к наноразмерным наполнителям наряду с сокращением удельного расхода позволяет намного повысить эксплуатационные характеристики материала [5].

Сильный эффект упрочнения, реализуемый уже при малых содержаниях наноразмерных частиц наполнителя, указывает на существование сильных межфазных-межкомпонентных взаимодействий на границах раздела матрица–наполнитель. Определяющим фактором этих взаимодействий является фрактальная природа наночастиц. Полимеры имеют сложную многоуровневую структуру, включающую молекулярный, топологический и надмолекулярные уровни. Наличие разного рода параметров, характеризующих эти уровни, усложняет получение аналитических соотношений между ними. Использование фрактальных размерностей в качестве однородных параметров для характеристики структурных уровней полимеров позволяет легко и строго получить указанные соотношения [6, 7]. Фрактальность структуры полимеров обусловлена существованием в ней областей локального порядка, исследование которых дает возможность установить ряд количественных аналитических соотношений.

В данной статье объектом исследования выбран внутрипромысловый трубопровод. Обычно для защиты трубопровода применяются различные лакокрасочные материалы, которые на сегодняшний день не в состоянии полностью решить проблему. Кроме этого, были специально выбраны уплотнительные манжеты газо-компрессоров и кольца нефтепромысловых насосов.

В качестве композиционного материала для антикоррозийной защиты трубопроводов был принят композиционный материал с составом эпоксидной смолы (ЭД-20) с бутадиен-стирольным каучуком (БСК) и в качестве наполнителя – наномедь.

Для изготовления манжет и колец использовался нанокомпозиционный материал, полученный на основе фторопласта (матрица) и наполнителя-меди.

Металлополимерные композиты (МПК) относятся к числу перспективных, но малоизученных областей современного материаловедения. В основном их использование к настоящему времени ограничивалось электропроводящими композициями для нагревательных устройств.

Большие возможности для их дальнейшего развития лежат в области нанокомпозитов, так как при использовании однородных частиц полимеров и металла существенным образом изменяются почти все физические и химические свойства как исходных компонентов, так и в целом нанокомпозита. За счет увеличения межфазных взаимодействий открывается возможность воздействия на электрофизические, физико-механические и химические параметры получаемых материалов контролируемой молекулярной архитектурой [8, 9].

1. Специфические особенности структуры дисперсно-наполненных полимерных нанокомпозитов

Полимеры представляют собой длинные гибкие цепи макромолекул. Число N (степень полимеризации) может достигать значительно больших значений (для полистирола N ˃ 10⁵).

В разбавленном растворе неперекрывающихся клубков полимерных макромолекул в хорошем растворителе радиус инерции одного клубка R G зависит от степени полимеризации N по скейлинговому (самоподобному) закону [10]:

R G = const ∙ a ∙ N^ν ,                  (1)

где а – эффективная длина, приходящаяся на один мономер; ν близко к 3/5.

В простых полимерах невозможно реализовать высокопрочное состояние [11]. Но оно с успехом реализуется в полимерных композитах, наполненных дисперсными наноразмерными частицами. Наполнение твердыми нано-дисперсными частицами с «активной» поверхностью придает получаемым полимерным композитам ряд полезных

для эксплуатации свойств: повышает жесткость, снижает коэффициент теплового расширения, повышает сопротивляемость ползучести и вязкость разрушения, повышает диэлектрическую проницаемость и т.д [11, 12]. В дисперсно-наполненных полимерных композитах наноразмерные частицы наполнителя с учетом вышеуказанного скейлин-гового соотношения формируют линейные пространственные структуры («цепочки»). В то же время при наполнении полимерных композитов дисперсными микрораз-мерными частицами агрегаты последних образуют фрактальный каркас (аналог фрактальной решетки) [13].

Ключевым структурным аспектом для дисперсно-наполненных полимерных нанокомпозитов является агрегация частиц нанонаполнителя. Параметр агрегации к( r ) частиц нанонаполнителя ( r – радиус наночастиц) можно рассчитать в рамках дисперсной теории прочности определенным образом.

Согласно дисперсионной теории прочности, предел текучести на сдвиг любого нанокомпозита зависит от содержания наполнителя и определяется как [14]

Gнк⋅bB тнк ТМ + ’ V")

где τ ' – предел текучести на сдвиг полимерной матрицы; G – модуль сдвига нанокомпозита; b – модуль вектора Бюргерса; λ – расстояние между исходными частицами нанонаполнителя в нанокомпозите.

В случае агрегации исходных частиц нанонаполнителя уравнение (2) принимает вид [14]:

τ

нк

= τ'М +

G нк ⋅ b B k ( r ) Х ^,

где k ( r ) - параметр агрегации, который служит показателем среднего увеличения размера агрегатов частиц нанонаполнителя.

Уравнение (3) описывает влияние агрегации исходных частиц на предел текучести нанокомпозита. Этот эффект важен как с теоретической, так и с практической точки зрения в силу известной склонности наночастиц к агрегированию, выражаемой соотношением [15]

k ( r ) = 7,5·10^–3· S s , (4)

где S_s – удельная площадь поверхности нанонаполнителя, м²/г, которая определяется следующим образом [16]:

^ = ^, ρ н ⋅ D p

где D_p – диаметр частиц нанонаполнителя; ρ – плот-

ность нанонаполнителя, определяемая по формуле

W

Р н = ---,

ϕ _н

ϕ – объемная доля нанонаполнителя в нанокомпозите; н

W _н – массовое содержание нанонаполнителя.

Из уравнений (4) и (5) следует, что уменьшение размера частиц нанонаполнителя приводит к увеличению S s , что усиливает склонность исходных частиц нанонаполнителя к агрегации. В свою очередь, расстояние между частицами нанонаполнителя в условиях их агрегации можно рассчитать следующим образом [17]:

Подставляя в (5) d = 3 и для меди р _dens = 8930 кг/м³, а = 14 нм, получим

⁶ ' 1°^б

^ =       _f   к D k - d ---- м ^/г ,            ⁽¹³⁾

8930 I D P I D

( 28 J       p

Х =

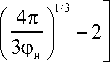
D ag

2  ,

где D_p - диаметр частиц наполнителя. Из (12) и (13) находим

где D - диаметр агрегата.

Число N частиц фрактального кластера радиусом R будет пропорционально величине R D ,

N ~ R D ,                    (8)

где D – размерность Хаусдорфа, которая была вычислена путем компьютерного моделирования Мекином [18] для трехмерного пространства, D = 2,495 ± 0,06.

Кроме этой модели, которая также широко используется при моделировании фрактальных кластеров, существует другая модель - ограниченная диффузией кластерная агрегация (DLCA), которая имеет также и другое название -«кластер-кластерная агрегация» (CCA) [19,20].

Для d = 3 в работе [20] получено D = 1,7. Однако когда в качестве наполнителя (как в нашем случае) используются частицы меди, полученные разбавлением порошка меди в электролитическом водном растворе ( copper deposited electrolytically from aqueous solution ), вышеприведенные значения фрактальной размерности D становятся неприемлемыми [21]. Плотность наполнителя р_н в случае агрегации вида «частица-кластер» записывается в виде

Р н = Р dens ( R / а ) D ^- d ,                      (9)

где р dens - плотность твердой меди; а - нижняя граница характерных размеров кластера. Для меди р dens = = 8930 кг/м³, а = 14 нм. Значения D в формулах (8) и (9) оцениваются экспериментально как [21]

D = 2,43 ± 0,03,                (10)

а для величины а установлено соотношение

1/ а и V - (0,23 V ),                (11)

где V - напряжение в электролите.

В работе [22] предложено рассматривать структуру дисперсно-наполненного полимерного композита как совокупность двух фракталов (мультифракталов) наполнителя с фрактальной размерностью D_k (в обозначениях работ [18, 21] D k = D ) и полимерной матрицы с фрактальной размерностью d f . Наряду с D k вводится в рассмотрение [17] фрактальная размерность агрегата частиц наполнителя d _н , определяемая соотношением

S_s = 410 R d ^{- d} ,                 (12)

где S_s - удельная площадь поверхности нанонаполнителя, рассчитываемая по формуле (5); R p - радиус частиц нанонаполнителя.

d n

410 1 D P I

I 2 )

б - 10^б

( D A D k d

8930I — P I ■ D„

I 28 J        ^p

Логарифмируя последнее равенство и разрешая относительно d _н, получим

d„ = d + — н lg

D P

б + lg[ ——

I 8930

—

- ( D k - d )( lg D p - lg28 ) lg-_P - lg410.

Остальные параметры, входящие в (3), определяются следующим образом. Общее соотношение между нормальным напряжением σ и напряжением сдвига τ имеет вид [23]

CT ^T= .

Напряжение т^ в (3) определяется согласно урав-

нению [14]

^т M =^т м ( 1 -ф н ^/3 ) ,

где тм - предел текучести при сдвиге матричного полимера; фн - объемное содержание нанонаполнителя, определяемое по формуле (6).

Модуль сдвига G _нк связан с модулем Юнга Е _нк простым соотношением [24]

G нк =    ' ,                      (17)

df где df - фрактальная размерность структуры нанокомпозита, определяемая по формуле df = (d-1)(1 + vнк),                (18)

где d - размерность евклидова пространства, в котором рассматривается фрактал нанокомпозита (в нашем случае d = 3); vнк - коэффициент Пуассона нанокомпозита, оцениваемый с помощью соотношения стнк 1 - 2 v т               нк

----=-----------.

Е_нк    б(1 + v _{H к})

нк             нк

Откуда находим

Е - б ст ^нк v = —нк----т— .

нк   бстнк + 2 Еж т        нк

Здесь а™ - предел текучести нанонаполнителя, определяемый по результатам механических испытаний, а Е_нк оценивается по формуле Коунто [25]:

Е нк = Е м ^1 —ф Н/2 )

EM

/ ф Н^/2 I E m + E н

( ,  (21)

где E m и E н - модули упругости полимерной матрицы и нанонаполнителя.

Величина модуля вектора Бюргерса Ь в для полимерных материалов определяется согласно уравнению

1/2

,      1 ( 60,5 | bR = — — в 101 C„ J

нм,

где C,  - характеристическое отношение, связанное

с размерностью d f уравнением

2d4

---------7Г +—.

d (d—1)( d — df)

Для теоретической оценки величины т_м в уравнении (16) необходим независимый метод определения параметра k ( r ) Х . Такой метод дает уравнение [25]

k ( r ) Х =

1/3

( 0,251 п D_;1 A  _₂

I W J

V        н       /

D p

.

В самом деле, подставляя (24) в (3), находим

т

М

т нк

^к ■ Ь в

( 0,251 п D P³ у³ _ 1 D p

V     W h    J       2

Соотношение (24) дает возможность найти реальный диаметр агрегатов частиц D ag . Действительно, из (4) с учетом (13) получим

7,5 ■ 6 40 3

k ( r ) = ---------- 8930 D

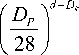
где D_p входит в знаменатель как безразмерная величина, равная числу нанометров в диаметре частиц наполнителя. Из (7) и (26) в условиях агрегации частиц наполнителя имеем

k ( r ) Х =

45 ■Ю³ ( D_p A d - D ^k

8930 D_p V 28 J

.

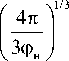
Приравнивая правые части уравнений (24) и (27), получим

45 ■Ю³ ( Dp A d - D ^k

8930 D_P V 28 J

4п Р

³ Ф н J

D ag

1/3

(0,251 пDP'3 A„

V    Wh    J

Разрешая последнее уравнение относительно D ag ,

находим

( 0,25 п D 1 ^/3

V    W h

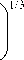
— 2

D P

1/3

45 ■Ю³ ( D P A d D ( 4 n A _₂

8930 D_p ( 28 ^J I 3 ф  I

P н

Формула (29) может использоваться для расчета реального диаметра агрегатов частиц наполнителя для рассматриваемого нами МПК при заданных значениях ф_н, W _н и D p в нм. В частности, при ф_н = 0,1157, W _н = 0,175, D k = 2,43 и D p = 60 нм, по формуле (29) получим D_ag = 213 нм.

Формула (29) применима и к другим МПК, если заменить в ней 8930 кг/м³ на плотность р dens металла наполнителя. Величина D _к при этом определяется экспериментальным путем с использованием формулы (9) с D = D _к и а = 14 нм [37] в случае агрегации вида «частица-кластер».

2. Дисперсно-наполненный композит как совокупность двух фракталов

В работах [22, 27] принята концепция структуры композита как совокупности двух фракталов - каркаса частиц наполнителя и самой полимерной матрицы. Их взаимодействие сводится в основном к «возмущению» структуры полимерной матрицы, которое производится каркасом частиц наполнителя. В физическом смысле понятие «возмущение» заключается в снижении степени ее локального порядка. Для аморфного состояния полимеров степень локального порядка структуры, определенная в рамках кластерной модели [27], осуществляет контроль важнейших свойств полимерной матрицы и, стало быть, всего композита в целом [32].

Учитывая важность фрактальной размерности поверхности наполнителя d н , рассмотрим влияющие на ее величину факторы. Как известно [22, 38], в дисперсно-наполненных композитах процесс агрегации исходных частиц наполнителя можно охарактеризовать двумя параметрами - фрактальной размерностью каркаса частиц наполнителя D _к, характеризующей их распределение по размерам, и параметром агрегации k(r), служащим показателем среднего увеличения размера агрегатов частиц наполнителя. Кроме того, показатель объемного содержания наполнителя ф _н также может служить одной из характеристик степени агрегации частиц наполнителя, поскольку процесс агрегации усиливается по мере роста ф _н [38].

На рис.1 приведена вычисленная по формуле (14) зависимость d _н от D p при фиксированном значении фрактальной размерности D_k = 2,43 и d = 3.

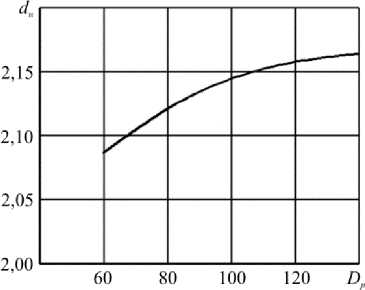
Рис. 1. Зависимость фрактальной размерности d _н поверхности агрегатов частиц наполнителя от диаметра частиц наполнителя D_p для рассматриваемого композита при фиксированном значении фрактальной размерности ( D _к = 2,43) каркаса частиц наполнителя

Fig. 1. Dependence of the fractal dimension d _н of the surface of the aggregates of the filler particles on the diameter of the filler particles D_p for the composite under consideration, for a fixed fractal dimension ( D _к = 2.43) of the carcass of the filler particles

поверхность с большей фрактальной размерностью вследствие ее большей шероховатости.

Зависимость d н от k ( r ) легко получается из формул

(12) и (4). Из (4) имеем

k ( r )10³

^s     7,5

Приравнивая правые части равенства (12) и (31), после логарифмирования получим

d _н

— d +

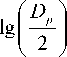
1g k ( r ) + 1g

7,5 ■ 410

На рис. 2 представлена вычисленная по формуле (32) зависимость d н от k ( r ) при фиксированных значениях D k = 2,43 и D p = 60 нм, при этом d н рассчитано по формуле (14), а k ( r ) по формуле (26).

Как видно из рис. 2, с ростом параметра агрегации k ( r ) увеличивается значение d н .

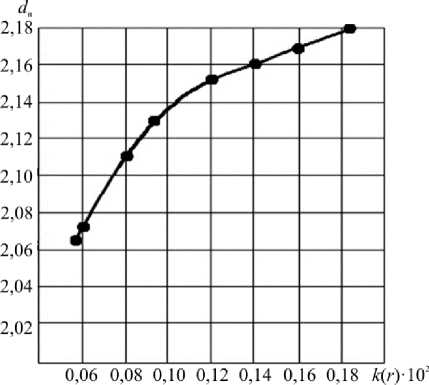
Рис. 2. Зависимость d _н от k ( r ) при фиксированных значениях фрактальной размерности d _н поверхности частиц наполнителя от параметра агрегации k ( r ) для рассматриваемого композита Fig. 2. Dependence of d _н on k ( r ) for fixed values of the fractal dimension d _н of the surface of the filler particles on the aggregation parameter k ( r ) for the composite under consideration

Из рис. 1 видно, что величина d н увеличивается с ростом диаметра наполнителя D p , что и следовало ожидать, поскольку при агрегации частиц большого диаметра их упаковка во фрактальный кластер образует