Свойства структуры и живые системы: сетевая модель экономики как механизм работы живого организма

Рассмотрение свойства структуры живых и неживых систем, двойственных сетей и экономики было начато в [20]. Живая система должна получать из окружающей среды больше энергии, чем затрачивает. Есть, конечно, свойства самоорганизации, приспособления к внешней среде, размножения, передачи качеств родителя потомкам. А также любопытство и резонанс, связанный с выбором партнеров, и многое другое. Но все это должен обеспечить внешний поток энергии, поступающий в живую систему, иначе она станет неживой.

Как с помощью неживой системы представить основное качество живой системы? Системы состоят из связанных в структуру элементов, в которых протекают процессы в виде потоков энергии. Виды энергии в этом мире известны, они одинаковы для всех систем. Особых видов живой энергии не обнаружено. Отличие живых и неживых систем может состоять в структуре связей элементов. Структура обладает такими свойствами, которыми не обладают процессы.

Разновидностью живой системы является экономика. Система производства продуктов должна получать от природы больше энергии, чем тратит, т.е. работает как живая система. Хозяйство доступнее для наблюдения, чем живой организм; это удобно для моделирования. Автор создал сетевую модель производства, которая представляет потоки продуктов комбинацией узловых и контурных токов с помощью двойственности открытых и замкнутых путей. Преобразования этих путей при изменении структуры связывает инвариант двойственности.

В физике это постоянство суммы рассеиваемых мощностей двух двойственных сетей при изменении их структуры (инвариант мощности, или закон сохранения потока энергии). В замкнутых путях и в разомкнутых путях сети потоки протекают независимо друг от друга. Можно использовать их взаимодействие для усиления потока в системе. Подобно тому, как живая система воздействует на внешнюю среду, увеличивая количество энергии в своем распоряжении.

Жизнь и внешний поток энергии

Естественные и искусственные неживые системы имеют коэффициент полезного действия (КПД) меньше единицы. Живые системы, хотя и подчиняются тем же физическим законам, но имеют видимый КПД больше единицы, поскольку получают из окружающей среды больше энергии, чем тратят. Хозяйство, как живая система также получает входной поток энергии, часть которого она преобразует в полезную работу (свободную энергию), а часть теряет.

П.Г. Кузнецов 8 января 1962 г. профессору МГУ Б.М. Левитану писал: «Интересным устройством (в термодинамическом смысле) является сам человек. В теле человека находится около 300 000 килокалорий. Каждые сутки человек расходует 3000 килокалорий. Если лишить его питания, то он сгорит за 90 суток. По этой причине человек должен работать. Однако из 3000 килокалорий в сутки в тепло и на обмен веществ человек расходует 2400. Примерно 600 килокалорий человек может превратить в физическую работу, после чего и эта энергия переходит к природе. Если на эти 600 килокалорий природа не отдаст человеку 3000 килокалорий, то такая работа нецелесообразна» [3, с. 448].

Таким образом, механизм работы живого организма состоит в том, что полезный поток энергии расходуется в двух направлениях – на поддержание работы организма (даже если он в покое), и на работу организма по добыче другого потока энергии, превосходящего затраты. В экономике эти направления выражаются как постоянные расходы (независимо от выполняемой работы) и переменные расходы (выполняемые для производства продукции и получения прибыли). Расходы целесообразны, если полученная энергия больше затрат.

Живые системы существуют за счет использования внешнего потока энергии. Основным источником энергии является солнечное излучение. Потоки энергии создаются как в неживой природе, так и в живой природе. Во времена охоты человек использовал энергию животных, 1 кв. км кормил одного человека. Во времена земледелия использовалась энергия, накопленная растениями в процессе фотосинтеза; 1 кв. км кормил 20 человек.

П.Г. Кузнецов писал об управлении внешним потоком энергии для усиления мощности: «Я хочу заметить, что принцип сохранения мощности, весьма отличается от других законов сохранения. Если мощность, как поток энергии – сохраняется, то его невозможно ни увеличить, ни уменьшить!!! Тем не менее, мы имеем многочисленные примеры, где имеет место усиление мощности» [2, с. 70].

У.Р. Эшби, один из пионеров кибернетики и сложных систем, рассматривал две стадии работы кочегара: «В первой стадии кочегар поднимает уголь в топку; в этой стадии энергия строго сохраняется. Попадание угля в топку представляет начало второй стадии, в которой энергия тоже сохраняется, по мере того как сжигание угля приводит к производству пара, и наконец, к вращению колес на заводе». Разделив процесс на две стадии, инженер может получить общее усиление мощности. (Схема усилителя умственных способностей // в сб.: Автоматы. – М.: ИЛ, 1956. – с. 281-305). Эти две стадии не противоречат законам сохранения, но описывают передачу энергии между элементами системы, т.е. структуру связей, благодаря которой возникает усиление мощности.

П.Г. Кузнецов развивает эту мысль: «… человек не может влиять на величину этого потока, т.к. изменение величины потока энергии – противоречит его сохранению. И тем не менее, … эффект усиления потока энергии все-таки имеет место… Если нельзя влиять на величину потока энергии, то можно влиять на его направление!!!

Типичным примером изменения направления потока энергии служит уже сельское хозяйство – изменения «направления» здесь означает переход в потенциальную энергию органических веществ.

Но мы не случайно ввели воздействие на поток энергии (или мощности) в форме изменения направления. Таков путь использования потока энергии ветра в изготовлении паруса, таков путь использования потока энергии в ветряной и водяной мельнице» [2, с. 71].

Таким образом, для работы живой системы необходим поток энергии, который протекает вне этой живой системы, а она изменяет его направление, используя для своей деятельности. Этот поток может быть создан неживой природой или другими живыми системами. Например, текущая вода, солнечное тепло – потоки энергии, созданные косной (по выражению Вернадского) материей. Дрова, полученные от деревьев, нефть и уголь, молоко и зерно, и т.д. – потоки энергии, созданные другими живыми системами. Таким образом, основой усиления мощности является изменение направления потока энергии, а это требует путей для протекания потока энергии, т.е. речь идет о структуре связей при взаимодействии живой и неживой систем.

Изменение направления, о котором говорит Кузнецов, выражается в том, что существует целый ряд циклов, которые возникают, меняются и исчезают по мере эволюции живого. Например, движение воды использовалось для перемещения по рекам и морям. Вызвано это природными циклами – испарение воды морей, перенос облаков к горам и выпадение осадков с последующим течением воды под действием силы тяжести вниз к морям. Затем падение воды с плотины использовалось для передачи вращения на станки завода. Другие свойства воды стали обеспечивать работу парового двигателя, где работает цикл нагрева и охлаждения и т.д.

Экономика и структура

Границы и структура, играют важную роль в экономике и политике. Изменение границ является целью политики, и как принято говорить ее продолжения другими средствами. В мире сетевых структур эти другие средства не всегда, и не только определяются боевыми действиями. Их часто заменяют информационные войны, информационно-финансовые войны в различных вариантах. Однако важнее то, что специализация и разделение труда, при выпуске сложной продукции увеличивает число связей между предприятиями и странами. Растут потоки продуктов, капиталов, людей, информации; создаются хозяйственные связи через границы между странами.

В живом организме потоки энергии и свойства структуры, которые обеспечивают усиление мощности, наблюдать и измерять достаточно сложно. Более наглядной и измеримой живой системой является экономика. Задача хозяйства состоит в получении из окружающего мира, от внешнего потока больше энергии, чем затрачивается. Тот факт, что основой потока является солнечная энергия, отмечал открыватель закона сохранения энергии Роберт Юлиус Майер. В 1845 году он писал в работе «Органическое движение в его связи с обменом вещества». «Поток солнечной энергии (силы) являющийся и на нашу Землю, есть та непрестанно заводящаяся пружина, которая поддерживает в состоянии движения механизм всех происходящих на Земле активностей». Кстати, его статья о законе сохранения энергии пролежала в столе редактора журнала 36 лет…

Вместе с тем только малая доля энергии Солнца поступает нашим живым системам. Из письма П.Г. Кузнецова академику АН СССР А.И. Опарину от 25 октября 1956 г. «Позавчера мною получено письмо, подписанное Вами. В нем сообщается, что только 10-13

части излучения Солнца приходится на биологические явления. Нет сомнения, что это очень небольшая часть солнечного излучения. Однако было время, когда и эта часть излучения рассеивалась в пространстве, а теперь обуславливает существование органической жизни на Земле». [3, с. 440]. Кузнецов подчеркивает, что эта часть исторически возрастает.

Экономическая система обеспечивает возрастание энергии, которая приходится на общество. Средний темп роста составляет около 4% в год. Эта величина связана с качеством преобразования потока солнечной энергии в процессе фотосинтеза. Через ресурсы этот поток путем технологических преобразований превращается в продукты, потребляемые людьми. Сумма технологий составляет сетевую структуру с механизмом усиления мощности.

Для моделирования механизма работы экономической системы необходимо применение математических методов оценки изменения процессов при изменении структуры. Сетевые модели позволяют осуществлять расчет изменения процессов производства, изменения хозяйственных связей, оценку результатов структурных реформ.

Описание экономической структуры содержится в модели затраты-выпуск, известной как задача межотраслевого баланса. Модель имеет простой математический вид, но в исходной постановке структура, сетевая модель, в явном виде не рассматривается. Модель затраты-выпуск описывает стационарное состояние экономики. При появлении новых отраслей, новых источников ресурсов, закрытии устаревших производств, необходимо рассматривать изменение структуры связей, используя сетевую модель.

В сетевой модели межотраслевого баланса [1, 4, 7] контурные токи могут дополнять узловые токи так, чтобы их сумма соответствовала потокам продуктов. Таким образом, свойства структуры позволяют представить потоки в живой системе комбинацией физических процессов.

Изменение структуры сетей

Сеть состоит из элементов: точек, ветвей, поверхностей, объемов. Рассмотрим сеть из ветвей. Ветвь, отрезок линии с двумя границами, (точками, или узлами). Ветвь имеет направление. Ветви могут иметь веса. Ветви могут соединяться границами. Схема соединения ветвей составляет структуру сети. Изменение структуры состоит в изменении границ между ветвями. Для соединения ветвей узлы границы сливают в один узел. Для разделения ветвей соединяющий их узел разделяют на два узла.

Ветвь считается неизменной и принимается за измерение. Вместе ветви составляют пространство сети. Координатами этого пространства являются пути. Каждая ветвь имеет свой путь, который проходит по ней от одной границы до другой. Если ветвь замкнутая, то путь замкнутый (контур). Если ветвь разомкнутая, то путь разомкнутый (открытый).

При соединении ветвей в связанную сеть пути могут проходить по многим ветвям. Путь имеет направление, состоит из ветвей, по которым он проходит, и выражается через эти ветви, с учетом их ориентации (плюс единица или минус единица). Путь, который проходит по ветвям, и возвращается в узел начала – это замкнутый путь; иначе – разомкнутый путь.

Путь можно выражать через другие пути, комбинируя составляющие их ветви. Набор линейно независимых путей составляет базис в пространстве сети. Базис контуров определяет подпространство замкнутых путей, а базис разомкнутых путей определяет подпространство разомкнутых путей. Эти подпространства независимы и дополняют друг друга до полного пространства сети.

При изменении структуры связанной сети если два узла соединяются, то возникает контур, исчезает разомкнутый путь. Если узел соединения разделяется на два узла, то исчезает контур, возникает разомкнутый путь. Соответственно меняются размерности их подпространств.

При изменении структуры базисные пути в новой сети можно выразить через базисные пути в старой сети. Обычно удобно рассматривать матрицу преобразования отдельных, свободных ветвей в связанную сеть, хотя это не обязательно. Коэффициенты в таком выражении образуют матрицу преобразования путей С . Это матрица преобразования структуры. Ее строки и столбцы имеют наглядный смысл:

• •    элементы строки показывают, какие ветви, с какой ориентацией, составляют путь;

• •    элементы столбцов показывают, в какие пути, с какой ориентацией входит данная ветвь, точнее, ее путь.

Матрица С состоит из двух подматриц, описывающих преобразование замкнутых путей ^mC и разомкнутых путей ^jC .

Соединения ветвей – это проекции тензора в разные системы координат структуры. Расчет разных структур с помощью одного решения как преобразование координат, единый метод расчетов различных структур, уменьшает объемы вычислений. На рисунке дан пример преобразования от свободных ветвей к связанным ветвям.

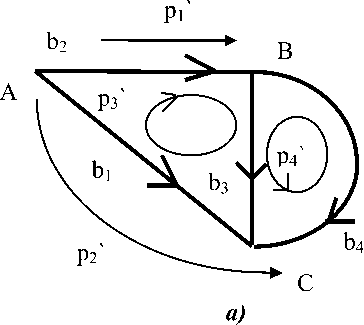
_b         b 2             b 3             ^b4

p 1             p 2             p 3              p 4

б)

Рис. 1. Базис замкнутых, m и разомкнутых, j путей в сети а – базисные пути в связанной сети; б – базисные пути в свободной сети

Коэффициенты базиса путей в связанной сети рп' через пути в свободных ветвях p_Q составляют матрицу преобразования путей: р_п = С рп :

\ а

Р \    Р1______ Р2 ______ рз ______р4

Р1  _________		1			j	j c
Р 2	1				j
Р з	–1	1	1		m	mc
Р 4			1	–1	m

Здесь j - разомкнутый путь, а m - замкнутый путь. В матрице строки показывают, какие ветви, с какой ориентацией, составляют данный путь. Элементы столбцов показывают, в какие пути, и с какой ориентацией входит данная ветвь.

Задача расчета цепи состоит в определении откликов в соединенных ветвях при заданных воздействиях в ветвях. Решение должно удовлетворять законам Кирхгофа о равенстве нулю суммы токов в каждом узле и суммы напряжений в каждом контуре. Токи и напряжения связаны законом Ома.

Матрица ^mC используется для расчета цепи с источниками напряжения. Это контурный метод расчета – воздействия внутри цепи, а базисом для откликов, токов в ветвях, являются контуры. Крон связывал независимые контурные токи в простейшей сети из отдельных ветвей, и контурные токи в соединенной сети; его матрица преобразования С транспонирована относительно матрицы преобразования путей.

Ортогональная (обратная и транспонированная) к С матрица, обозначается как А, и описывает преобразование взаимного базиса путей при изменении структуры. Каждый вектор взаимного базиса ортогонален всем векторам прямого базиса, в данном случае, базиса путей. Вектор взаимного базиса сети связывает две поверхности равного потенциала, определяя разность потенциалов, т.е. напряжение. Крон и рассматривал эту матрицу как преобразование напряжений. Таким образом, мы имеем дело с двумя сетями: 1-сетью ветвей, в которых протекают токи, и 2-сетью эквипотенциальных поверхностей, ортогональных 1-ветвям, которые определяют напряжения.

Матрица А также состоит из двух подматриц ^m А и ^jА . В электротехнике матрица ^jА используется для расчета цепи с источниками тока. Это узловой метод расчета – заданы внешние воздействия (ток входит в сеть через один узел, покидает ее через другой узел), а базисом для откликов, напряжений на ветвях, являются разомкнутые пути.

Двойственные сети и закон сохранения потока энергии

Асимметрия замкнутых и разомкнутых путей в сети разрешается существованием двойственной сети, в которой столько же ветвей, но каждому замкнутому пути соответствует разомкнутый путь, а разомкнутому пути – замкнутый путь. Размыканию контуров в данной сети соответствует замыкание разомкнутых путей в двойственной сети, и наоборот [23]. В одной сети возникает соединение, а в другой сети ему соответствует разъединение. Сеть существует как единое целое, состоящее из двух частей – данной сети и двойственной сети.

При соединении двух узлов в сети разделяется один узел на два узла в двойственной сети. В одной сети при этом возникает контур, исчезает разомкнутый путь, а в двойственной сети возникает разомкнутый путь, исчезает контур. Замкнутому пути в одной сети соответствует разомкнутый путь в двойственной сети, и наоборот. В двойственных сетях при изменении структуры постоянна сумма независимых замкнутых путей и разомкнутых путей, а, следовательно, суммарная размерность соответствующих подпространств путей.

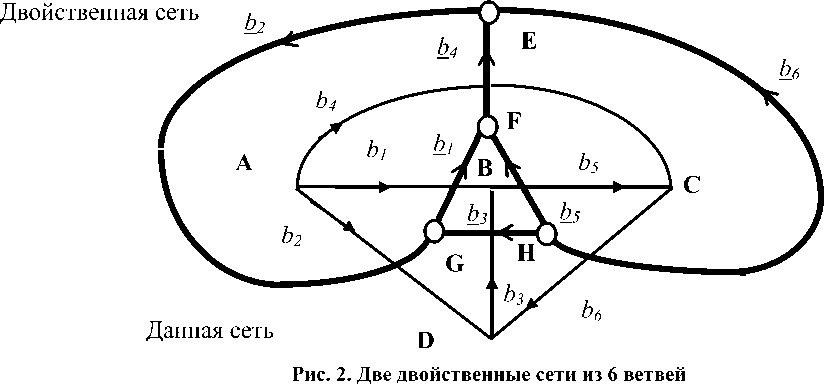
Структуру двойственной сети определяет матрица  C□' , которая является ортогональной к матрице преобразования путей исходной сети, CH'D = AD □ = (CH'D t) .

Каждая из этих сетей также состоит из двух частей: замкнутые пути и разомкнутые пути, заданные своими базисами. В каждой сети сумма базисов замкнутых и разомкнутых путей постоянна при любых соединениях, и равна числу ветвей. В двух двойственных сетях сумма замкнутых базисных путей и сумма разомкнутых базисных путей постоянна при любых соединениях, при любой структуре и равна числу ветвей. Таким образом, в каждой из сетей при изменении соединений количество замкнутых и разомкнутых путей меняется, а в сумме двух сетей остается постоянным.

При этом каждой 1-сети соответствует 2-сеть эквипотенциальных поверхностей, которые также образуют замкнутые и разомкнутые пути, определяющие напряжения.

Матрицы преобразования путей базиса p □ в базис p □ – матрицу C □ и матрицу обратного преобразования C □ , получим перемножением матриц преобразования от свободных путям к связанным путям, и обратно. Матрицы преобразования имеют нулевые блоки выражения разомкнутых путей через замкнутые пути (выделены жирными линиями):

3

ОС p 1 `

p 2 `

p 3 `

p 4 `

p 5 `

p 6 `

ОС

3 p 1 ``

p 2 ``

p 3 ``

p 4 ``

p 5 ``

p 6 ``

p 1 ``

1

–1

1

m

p 1 `

1

–1

m

p 2 ``

–1

1

m

p 2 `

1

m

p 3 ``

1

m

p 3 `

1

1

m

С [3 = p 4

–1

1

1

–1

1

j Ср J      а

А = p 4 `

1

–1

1

–1

j

p 5 ``

1

j

p 5 `

1

j

p 6 ``

1

–1

1

j

p 6 `

–1

1

1

j

m

m

m

j

j

j

m

m

m

j

j

j

Такой же нулевой блок есть и в матрицах преобразования от базисов свободных ветвей к базисам связанных ветвей, и наоборот. Это связано с тем, что разомкнутый путь нельзя выразить через замкнутые пути, которые определяют новое измерение.

Потоки в замкнутых и разомкнутых путях даже в одной и той же ветви протекают независимо друг от друга. Это важное структурное свойство может действовать как механизм усиления мощности. Открытые пути представляют базис для потоков от внешних воздействий, а замкнутые пути – базис для потоков от внутренних воздействий, что позволяет связать их структурно для усиления друг друга.

Самая простая сеть – это одна ветвь. Ветвь состоит двух частей: в одной части она разомкнута, и есть разомкнутый путь, а в другой части она же замкнута, и есть замкнутый путь. В каждой части ветви путь (разомкнутый или замкнутый) есть базис. Ему соответствует взаимный базис: две ортогональные поверхности, проходящие через границы всей ветви, или только части ветви, где расположен вес, сопротивление. В электротехнике поверхности равного потенциала задают напряжение, которое возникает на одном конце сопротивления, и плавно понижается до значения на другом конце. Происходит падение напряжения, которое действует на заряды свободных электронов в проводнике, что вызывает их движение от большего потенциала к меньшему потенциалу. Подобно тому, как вода течет с горы в долину. В электротехнике принято считать, что ток течет в обратную сторону, в сторону движения положительных зарядов, но это проблема электротехников.

Крон полагал, что строки и столбцы матрицы А не имеют такой наглядной интерпретации, как для матрицы С. Оказалось, что матрица А данной сети является матрицей С для двойственной сети, где ее строки и столбцы имеют аналогичный смысл, а подматрицы замкнутых и разомкнутых путей меняются местами. И наоборот, матрица С данной сети является матрицей А для двойственной сети.

Два подпространства замкнутых и разомкнутых пути двойственные, т.е. они дополняют друг друга до полного пространства сети. Они представляют единую сеть во всей совокупности ее замкнутой и открытой структуры, подобно известным с древности примерам двойственности.

Понятие двойственности связано с взаимным дополнением противоположностей. Идея двойственности в мифах древних народов дана как Геб и Нут у египтян, Ки и Ан у шумеров, Пракрити и Пуруша у индийцев, Инь и Ян у китайцев, Ометикутль и Омесигуатль у ацтеков, Ахриман и Ормюзд у персов – это названия богов или активных двойственных начал, взаимодействие которых приводит в движение мир. Стороны двойственности вступают в союз, где образуют целое, обладающее способностью к развитию. Так, Пракрити и Пуруша объединяются в Прадхане, Ян и Инь сливаются в Дао, Ахраман и Ормюзд соединяются в Митре, Ометеотль образует единое для Ометикутля и Омесигуатля. Об этом писали русский конструктор логических машин Александр Николаевич Щукарев в 1934 году [12] и В.В. Попков [8] в 2001 г.

Матрица решения контурной двойственной сети соответствует матрице решения заданной узловой сети. Аналогично, матрица решения двойственной узловой сети соответствует матрице решения заданной контурной сети, поскольку они подчиняются инварианту двойственности . Он состоит в постоянстве суммы метрических тензоров (матриц решения) двух двойственных сетей при изменении их структуры. В физике этому соответствует закон сохранения потока энергии. В данном случае это постоянство суммы рассеиваемых мощностей двух двойственных электрических цепей при изменении их структуры. Инвариант мощности Крона, как оказалось, состоит в том, что мощность меняется при изменении соединений в одной цепи, но постоянна сумма рассеиваемых мощностей в двух цепях с двойственной структурой при изменении их соединений.

Инвариант двойственности имеет структурное содержание и физическое содержание . Что из этого первично, а что вторично – подобно решению вопроса, следует ли из закона сохранения импульса однородность пространства, или наоборот. Принято связывать законы сохранения со свойствами симметрии физических систем. «…Симметрия понимается как инвариантность физических законов относительно преобразований входящих в них величин. Наличие симметрии приводит к тому, что для данной системы существует сохраняющаяся физическая величина. Если известны свойства симметрии системы, можно найти для неё законы сохранения, и наоборот.

Законы сохранения механических величин (энергии, импульса, момента) обладают всеобщностью. Их симметрии можно рассматривать как симметрии пространства-времени (мира), в котором движутся материальные тела. Так, сохранение энергии связано с однородностью времени, с инвариантностью физических законов относительно изменения начала отсчёта времени (сдвигов во времени). Сохранение импульса и момента количества движения связано соответственно с однородностью пространства и изотропностью пространства (инвариантность относительно вращений пространства)». [13].

Такую роль симметрии доказывает теорема Э. Нётер, которая утверждает, что каждой непрерывной симметрии физической системы соответствует закон сохранения:

• •    однородности времени соответствует закон сохранения энергии,

• •    однородности пространства соответствует закон сохранения импульса

• •    изотропии пространства соответствует закон сохранения момента импульса, и т.д.

Для структуры закон сохранения обеспечивает не симметрия, а двойственность , как дополнение двух противоположностей, которое соединяет их в общем понятии. Например, две сети с одинаковым набором ветвей, но с двойственной структурой их соединения. В двойственных сетях сумма рассеиваемых мощностей есть инвариант относительно соединения ветвей.

Математическое содержание инварианта двойственности следующее. Пусть в сети нет потоков энергии, воздействий, откликов, а веса (сопротивления) ветвей равны единицам. Есть только соединенные ветви, и пути в ветвях. Инвариант двойственности дают четыре соотношения для двух видов сетей и двух типов путей. Например, инвариант связывает матрицы преобразования замкнутых путей и разомкнутых путей в данной сети:

mCt (mC mC t)-1 mC + jAt (jA jA t)-1 jA = I где I – единичная матрица. Это структурное содержание инварианта, свойство собственно структуры сетей, которое не зависит от физических свойств ветвей, от потоков энергии.

Аналогично, инвариант двойственности связывает матрицы преобразования замкнутых путей и разомкнутых путей в двойственной сети:

^m C t (^m C ^m C t )^{-1 m} C + ^j A t (^j A ^j A t )^{-1 j} A = I

С пониманием того, что mC = jA, а mC = jA. Также инвариант двойственности выражается для совокупности замкнутых путей данной и двойственной сети mCt (mC mC t)-1 mC + mCt (mC mC t)-1 mC= I

И, наконец, для совокупности разомкнутых путей данной и двойственной сети jAt (jA jA t)-1 jA + jAt (jA jA t)-1 jA = I

Смысл инварианта состоит в том, что для базиса замкнутых путей сумма прямых метрических тензоров двух двойственных сетей равна метрическому тензору свободных контуров. Для базиса открытых путей сумма обратных метрических тензоров двойственных сетей равна метрическому тензору свободных разомкнутых ветвей.

Сначала было найдено физическое содержание инварианта двойственности [1, 4], т.е. постоянство рассеиваемой мощности в двух двойственных цепях при изменении структуры. Для электрических цепей было обнаружено, что сумма рассеиваемых мощностей двух двойственных цепей постоянна при изменении соединения их ветвей.

Данный закон, как отмечено выше, продолжает ряд других законов сохранения, т.е. физических законов, согласно которым некоторое свойство замкнутой системы остается неизменным при каких-либо изменениях в системе.

Закон сохранения потока энергии связан с двойственностью структуры пространства. Свойство замкнутости системы состоит в том, что при изменениях структуры сами ветви не меняются – их остается столько же и с теми же метрическими характеристиками (например, комплексными сопротивлениями, или проводимостями). Закон сохранения потока энергии указывает на возможность существования двойственного пространства.

Замыкание открытого пути дает новое измерение пространства

Рассмотрим подробнее отличие замкнутых и разомкнутых путей. Замкнутый путь можно выразить через слияние или разделение контуров, или через разомкнутые пути. Например, если концы-узлы двух разомкнутых ветвей соединить, то получится замкнутый путь. Т.е. можно выразить как через замкнутые, так и через разомкнутые пути.

Разомкнутый путь нельзя выразить через замкнутые пути – как ни соединяй контуры, а разрыва не получится. Можно сделать разрыв, но это уже особое действие. Такова асимметрия пространства. Математически это проявляется в том, что квадрант матрицы преобразования, соответствующий выражению открытых путей через замкнутые пути, состоит из нулей, что и показано выше на примере.

Причина в различии их геометрических размерностей. Открытые пути все принадлежат одномерному пространству; их можно расположить вдоль одномерной линии. Замкнутый путь охватывает часть двумерной поверхности. Не разрывая контур нельзя сделать замкнутый путь принадлежащим только линии. Так замкнутый путь вводит новое измерение пространства.

Двумерные сети, элементы которых суть куски поверхностей, обладают таким же свойством. Отрезок имеет два конца. У кольца нет начала и конца, но в нем «спрятан» один узел – «зародыш» места разрывания. Эти рассуждения подтверждаются математически. Так и поверхность – у нее есть границы в виде линий-отрезков. Принято рассматривать треугольники, квадраты, пятиугольники, чтобы придать наглядную форму одномерным границам. Считая путь в 2-сети как последовательность кусков поверхностей, связанных своими линиями-границами, получим, что для любой фигуры все такие пути открытые, разомкнутые. Замкнутый путь возникает тогда, когда фигура ограничивает замкнутое пространство, например, шар, или куб. Но это добавляет новое измерение, объем. Открытую поверхность нельзя выразить через набор шаров – нужно разрывание.

Подобные рассуждения справедливы и для большего числа измерений. Введение четырехмерного цикла – контура среди объемов – возможно только при охватывании четвертого измерения. И так далее. Так простые операции соединения и разъединения в структуре требуют появления (проявления) новых измерений в пространстве.

Двумерные существа, живущие на поверхности в мысленных опытах по теории относительности, могли бы через построение замкнутой поверхности узнать о существовании третьего измерения. Они должны начертить на поверхности четыре треугольника, соединить их стороны – и получить тетраэдр, т.е. трехмерный объем. Таким образом, проявится новое измерение пространства, в которое погружено их плоское пространство. Смогут ли они при этом осознать наличие объема, не «вылезая из поверхности», например, увидеть противоположную стенку – другой вопрос.

Сетевая модель межотраслевого баланса

Экономика как физическое явление возникает при разделении труда, специализации. Эквивалентный обмен создает носитель обмена, деньги. В экономике известна двойственность потоков продуктов и денежных средств.

Отрасли потребляют ресурсы и поставки, выпускают продукты, удовлетворяют спрос. Задан спрос y и мера потребления поставок для производства. Меру (метрику) взаимного потребления отраслями задает коэффициент прямых затрат (КПЗ) a . Это, например, количество угля для производства электроэнергии. Нужен расчет валового выпуска отраслей X , который обеспечивает спрос (план) y и поставки x .

^X =  x ар+ y .

Поставки продукта отрасли ОС для выпуска продукта отрасли р выражаются через КПЗ:

• ^x ар = a ар X3 .

Поток ресурсов rур задает коэффициент b _у^, – количество ресурса у для производства продукта отрасли :

• ^r ур = b ур X 3 . .

Решение дает обратная матрица Леонтьева, (I – A). Порядок матрицы для реальных задач составляет тысячи строк и столбцов, время расчета превышает сроки планирования.

Модель открытая – любую отрасль можно сделать ресурсом (и наоборот). Можно добавить или исключить отрасли; с изменением состава поставок и ресурсов – провести структурные преобразования. В сетевой модели токи представляют потоки продуктов, а напряжения – финансовые воздействия (потоки денежных средств).

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 12 № 3 (32), 2016, ст. 3

Промышленность

Торговля

Ток

«Вихри» магнитного потока

Добыча природных ресурсов

Банки

Население

Рис. 3. Аналогии сетевой модели электромагнитного поля Максвелла (слева) и сетевой модели товарно-денежного оборота в экономике (справа)

Сетевая модель позволяет представить процессы и структуру исследуемой предметной области. Контурные и узловые токи, которые в каждой ветви могут вызывать внешние и внутренние воздействия, позволяют использовать свойства структуры для моделирования системы с усилением мощности. Проблема создания сетевых моделей сложных систем состоит в поиске аналогий между величинами сети и предметной области, а также соответствия их структуры, которая представляет связи между элементами системы. Строгих методов создания сетевой модели нет, в каждом случае это, как писал Крон, скорее искусство, чем наука.

Токи в мертвой сети не могут напрямую представить потоки продуктов в живой экономике. В сетевой модели экономики для решения этого противоречия связаны ортогональные величины замкнутых и разомкнутых путей. Это обеспечивают источники в контурах. Их величина определяется поставками между отраслями. Потоки продуктов в экономике (живой системе) представляет комбинация двойственных контурных и узловых токов в неживой электрической цепи:

в отраслях:

p       p=p -1

vol jot - *ot                      3 ot . Bi/ \ 23i i /     pp ^_1 3

Xp-In+Linp-(a (%) y -y aayy +(^) y +-+(a#)  у , i=i в поставках между отраслями: 11=p        p=p-1

«0 та , у -a _v / x В x ^p  Im* imB       ⁽ a )3 ) y

1= 1           At⁼¹

ресурсов, потребляемых отраслями:

p                  p=P -1

rMrV^b, ( y “+ X( a .„)“ y⁸ ) p= 1                    g=0

Суммы двойственных контурных и узловых токов численно равны потокам продуктов в отраслях, поставках и ресурсах.

В процессе обмена потоки денег не текут навстречу потокам продуктов, по открытым путям, а проходят по замкнутым путям. Продукты перемещаются со склада на склад. денежные средства перемещаются с одних счетов на другие счета в банковской системе.

Продукты в сетевой модели возникают под действием внешнего спроса , представленного узловым током. Спрос на конечную продукцию определяет всю технологическую цепочку, которая эту продукцию производит. Узловые токи не дают точного представления потоков продуктов . Их дополняют двойственные контурные токи – внутренние источники .

Сетевая модель межотраслевого баланса [1, 4, 7] выражает потоки продуктов в отраслях, поставках и ресурсах как сумму контурных и узловых токов в эквивалентной электрической цепи. Цепь – неживая система, она только рассеивает поток энергии. Производство – живая система, она увеличивает поток энергии в виде продуктов жизнеобеспечения. Для представления живой системы моделью в виде неживой системы использованы свойства структуры. Узловые токи протекают в открытых путях, контурные токи протекают в замкнутых путях. Базисы этих путей образуют независимые подпространства в пространстве сети, что выражается в ортогональности их матриц преобразования.

Благодаря этому токи в контурах дополняют узловые токи в открытых путях так, чтобы их сумма соответствовала потокам продуктов. Таким образом, свойства структуры позволяют представить потоки в живой системе комбинацией физических процессов. При этом контурные и узловые токи протекают в одних и тех же ветвях, но вызваны разными источниками воздействия.

Контурные токи в сетевой модели выполняют две функции.

Во-первых, компенсируют узловые токи в поставках. Эти контурные токи в ветвях поставок равны узловым токам по величине, но противоположны по направлению. Тогда сумма токов в поставках равна нулю. Сумма токов в ветвях отраслей и ветвях ресурсов равна спросу. Здесь полные токи в сети соответствует выпуску потоков продуктов в натуральном хозяйстве, т.е. только конечного спроса без поставок между отраслями.

Во-вторых, далее источники напряжения изменяем так, что они создают рост контурных токов, которые соответствуют требованиям поставок, т.е. структурным связям отраслей. Эта часть контурной сети отображает взаимодействие субъектов в структуре хозяйственных связей при разделении труда и специализации.

Сумма спроса определяет совокупность средств жизнеобеспечения людей в настоящий момент (период времени). В отчетности этому соответствует потребление домашних хозяйств и расходы на государственное управление.

В сетевой модели экономики поток продукта представлен тремя видами узловых и контурных токов в одномерных каналах-ветвях. Каждому току соответствует свое напряжение – разность потенциалов на ортогональных поверхностях. Нулевой потенциал – «заземление» – соответствует природе, поставляющей энергетические, минеральные и другие ресурсы. Потенциал природы принимаем за ноль. Мы ничего не платим природе деньгами, и она у нас ничего за деньги не получает.

Потенциал каждого последующего узла представляет цену продукта на выходе данного производства, разность потенциалов соответствует добавленной стоимости. Аналогичная ситуация возникает при поставках продукции между отраслями технологической цепи.

Постоянные издержки и состояние покоя организма

Добыча ресурса добавляет энергии, создает прирост потенциала, что соответствует добавленной стоимости. Потенциал следующего узла есть полная цена продукта по затратам до этого участка.

Контурное напряжение добавляет цены и добавленной стоимости, как на поддержание стабильного состояния, так и на развитие продукта с добавленной стоимостью структуры, т.е. с развитием специализации.

Контурное напряжение также добавляет стоимости, связанные с транспортировкой, логистикой, составляющей сегодня до 90% времени производства сложного продукта.

Узловое напряжение и контурное, вместе с токами, приводящее производство к работе без структуры, без специализации – как бы натуральное хозяйство – можно рассматривать как состояние покоя организма, но в котором ему надо расходовать энергию.

Это аналог постоянных издержек в производстве. Обеспечение процесса жизни, потребление энергии, обмен с природой. Узловое, внешнее воздействие требует расхода энергии, а контурное напряжение добавляет к падению энергии в открытом контуре столько, чтобы вывести производство или организм в состояние гомеостаза. Поступление энергии равно расходу.

Контурные токи и напряжения, отражающие специализацию, дающие поставки – представляют развитие, рост производства сверх текущих потребностей. Как по росту потока продукции, так и по добавлению стоимости через постепенное повышение потенциала каждого следующего узла в технологической цепи.

В двойственной сети контурные и узловые токи представляют потоки денег, а напряжения – требования на производство продуктов. Здесь продукты порождают деньги, которые за них платят, а потребление создает заказ на новый выпуск продукта.

Живая система как замкнутая и открытая сеть

Структуру сетевой модели производственной системы можно представить как основу механизма работы живой системы. Взаимодействие открытых и замкнутых потоков можно рассматривать как систему усиления мощности. Это позволяет применять в сетевой модели экономической системы токи замкнутых и разомкнутых путей, которые дополняют друг друга для представления потоков продуктов.

Так может работать и живая биологическая система – за счет организации структуры связей элементов, в которых протекают потоки энергии известных видов.

Напряжение на ветвях сети соответствует побудительным импульсам в живой системе, которые дают сигнал на поддержание жизни. Узловые токи и напряжения моделируют воздействия внешней среды на организм, потребности расхода энергии на согревание, сигнальную систему и другие функции. Структурной средой этой внешней системы является базис открытых путей. Это характеризует организм как открытую систему.

Внутренняя система, работающая в контурах, отвечает за реакцию организма на внешние воздействия. Внутренние воздействия – импульсы дополняют внешние потоки до баланса обмена энергией с внешней средой.

При активном действии организма на внешнюю среду внутренние импульсы создают потоки, которые обеспечивают расход энергии больше потребностей равновесия – до уровня, когда ответный поток из внешней среды обеспечит рост потребления энергии также и для других организмов, необходимых для продолжения рода, развития жизни.

Исходным мотивом для экономической системы и живого организма является внешнее воздействие. Оно возникает как поток, который входит в систему, проходит по ней и выходит. В живой системе это поток энергии, нагревающий или охлаждающий систему – в зависимости от ее температуры. Или поток механической энергии, требующий движения организма и нужных реакций в опорно-двигательном аппарате. В экономической системе – поток спроса для обеспечения жизни людей и управления обществом, включая обеспечение безопасности.

Генерируют взаимодействие внешней и внутренней подсистем потоки сигналов. В экономике это план (спрос), в биологии – инстинкты. Аналог в сети – узловой ток, который входит в один узел сети и выходит из другого узла, образуя открытый, разомкнутый путь.

Напряжение на ветвях сети соответствует побудительным импульсам в живом организме, которые дают сигнал на поддержание жизни. Узловые токи и напряжения моделируют воздействие внешней среды на организм, потребности расхода энергии на согревание, сигнальную систему и другие функции. Структурной средой этой внешней системы является базис открытых путей. Это характеризует организм как открытую систему.

Внутренняя система, работающая в контурах, отвечает за реакцию организма на внешние воздействия. Внутренние воздействия – импульсы дополняют внешние потоки до баланса обмена энергией с внешней средой.

При активном действии организма на внешнюю среду внутренние импульсы создают потоки, которые обеспечивают расход энергии больше потребностей равновесия – до уровня, когда ответный поток из внешней среды обеспечит рост потребления энергии до обеспечения расхода других организмов, необходимых для продолжения рода, развития жизни.

Внешнее воздействие вызывает отклики в виде потоков в системе. Они возникают под действием разности потенциалов на узлах, которые являются откликом на внешние потоки. Внешние потоки подчиняются законам физики, согласно которым они не могут создать в сети больше энергии, чем принесли с собой. Внешние потоки дают сигнал внутренним воздействиям, а на них откликом является внутреннее движение в системе. В качестве реализации такого движения возникает, генерируется воздействие внутри системы. Это внутренние потоки, которые также подчиняются законам физики.

Внутреннее движение протекает в виде потоков в замкнутых путях, контурах. Эти потоки протекают только внутри системы и не имеют выхода в окружающую среду. Но при этом внутренние потоки и создают воздействие на внешний поток энергии, чтобы получить часть этого потока себе в количестве, превышающем воздействие в такой степени, чтобы эта деятельность была целесообразной.

Советская энциклопедия . 1969-1978 .