Свойства волны, преломленной под отрицательным углом

В настоящее время постулируется следующая система волн, возбуждаемых при падении плоской волны на границу раздела сред соответственно с J -^- и 52^2. [1]:

• 1)    падающая под углом φ плоская волна из первой среды;

• 2)    отраженная в первую среду;

• 3)    преломленная под углом Q волна во вторую среду.

Однако, если учесть, что волновое уравнение имеет решение в виде суперпозиции двух встречных волн в любой среде, то система собственных волн, возбуждаемых в граничащих средах, выглядит так, как схематично показано на рис. 1.

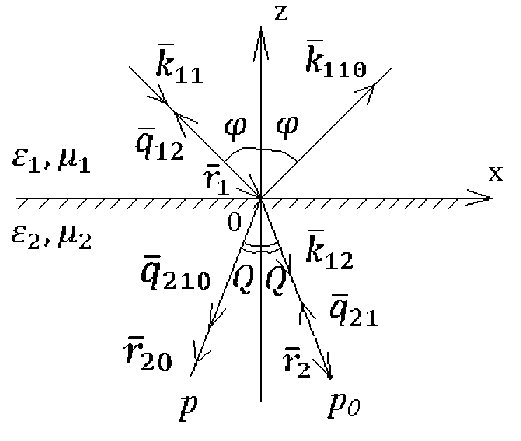
Рис. 1. Система собственных волн

Согласно данной системе, в результате падения плоской волны с волновым вектором    на гра ницу сред, возбуждаются волны:

отраженная в первую среду волна по направлению ;

преломленная во вторую среду с волновым вектором ;

обращенная волна во второй среде с волновым вектором ;

обращенная волна в первой среде с вектором ;

отраженная волна во вторую среду с вектором

.

Последняя волна и есть волна с отрицательным углом преломления Q, рис. 1.

В работе [2] наличие данной волны среди собственных волн связано не с отражением от границы обращенной волны, а со свойствами среды 2, имеющей как бы отрицательный коэффициент преломления. Такие среды в классе сплошных сред в настоящее время не найдены.

О существовании волн типа 0- p (рис. 1) отмечено в работах [3, 4, 5].

Если допустить, что причиной возбуждения волны 0-p (рис. 1) является указанный в данном сообщении физический механизм, связанный с отражением обращенной волны, то можно написать уравнение волны с отрицательным углом преломления:

E(p) = E^l + y.^jJ^OTe1®^»1®^

,

,        – коэффициенты отражения Френеля.

Из (1) следует, что в слабопоглощающих прозрачных средах волна 0-p сильно затухает из-за ма- лости коэффициентов отражения. В средах с заметной комплексной частью вектора волна также сильно затухает из-за поглощения во второй среде. Таким образом, экспериментальное наблюдение волны 0-p в большинстве сплошных сред затруднено. Она хорошо наблюдается в искусственных, вообще говоря, несплошных средах [6].