Symmetric Key Encryption using Iterated Fractal Functions

Published Online April 2017 in MECS DOI: 10.5815/ijcnis.2017.04.01

Now a day, a huge amount of data in terms of text, image, audio and video need to be transmitted over the unsecured network. The requirement of a secure communication system arises so that illegal acquisition, modification, alteration, copying and unauthorized accessing can be prevented and data must be transferred with original contents.

The art of converting a plain image into an unidentifiable stage known as cipher image is called cryptography [1]. Cryptography can be achieved with any of two methods: a traditional method, based on the application of number theory and algebra and another based on the application of the theory of dynamical system. In 1976, Diffie-Hellman established one of the earliest examples of public key exchange protocol in the field of cryptography [2]. The concept was to calculate shared key based on the prime numbers existed in available key size. After a long time, M. Alia et al. [3]

A detailed fractal geometry especially the speed of its generation is utilized in the encryption process. Before invention of public key algorithm with fractal, an author had reviewed various public key algorithms such as DES, RSA, ECDH etc and its applications like key exchange, data encryption and digital signature [5]. A fundamental explanation about the number theory particularly in the field of cryptography is discussed [6].

Fractals [7] are non-regular geometric shapes that have the same degree of non-regularity on all scales. A project was carried out in 2003 to encrypt a message with the help of random numbers and Mandelbrot set fractal. At that time fractal was not so much popular in a cryptography system. Author succeed to encrypt the data but unable to decode the same. A perfect decoder required a mapper so that no number came out twice [8]. In 2004, USA navy published the patent which highlights the importance of fractal as an encryption/decryption key in a cryptosystem [9]. A new approach to encryption using fractal geometry is discussed by the author in which a fractal is generated by using some initial parameters and then use it to encrypt a predetermined length of the message by using fractal orbits to corresponding alphabet mapping [10].

Besides using Mandelbrot set, many other fractal functions have been used to design a secure cryptosystem. In 2009, authors utilized the self-similarity property of IFS fractal and applied double enciphering and deciphering methods to obtain relatively efficient cryptosystem [11]. Later an improved RSA system is proposed by the authors again using the same IFS based fractal attractor [12]. A cryptosystem is designed to implement an asymmetric cryptographic approach to encrypting digital Images. The author utilized the complex mathematical structure and deterministic nature of fractal to propose a new public key cryptosystem based on IFS. It has been observed that the proposed system was more effective in terms of key space, key generation time and time required to encrypt/decrypt the data [13]. In [14], authors achieve a better PSNR test value while using hash algorithm MD5 and fractal function to design a cryptosystem. To prevent key exchange, the author proposed a model to generate a realtime encryption/decryption keys using quaternion Julia fractal image [15]. A complex structure and chaotic behaviour of fractal make it difficult to predict the key structure.

This paper proposes a cryptosystem in which shared key is generated using Mann iterated fractal function and Ishikawa iterated fractal function. Since fractal function works on the feedback system, the used one step and two steps iterated functions enhance the complexity of the key generation process. The proposed cryptosystem achieved a highly secure communication environment by creating a shared secret key between the both parties without exchanging them over the network. The paper also discusses the performance of the system in terms of key space, key sensitivity and time required to execute the process.

The Paper is organized as follows: Section II describes the related terminologies and related terms definition used in the method. A previous literature review is discussed in section III. Section IV discusses the proposed algorithm flow in detail. The simulation result and performance analysis are discussed in section V, which is followed by the conclusion of the study.

• II.    Preliminary Study

The symmetric key algorithm has a unique key used to encrypt as well as decrypt the data. In general, key needs to be transmitted through the communication network and hence negotiating the security of the cryptosystem. A possible way to protect the key hacking is by generating a secret key on the receiver side itself. The relationship between fractal functions i.e. Mandelbrot set and Julia set is utilized to generate the secret key on both sides which in turn secure the key to being hacked by the unauthorized entity.

• A. Fractal

Fractals are an infinitely complex pattern that is selfsimilar across different scale [16]. The Mandelbrot and Julia set are a kind of escape time fractal and constructed using same function i.e. z²+c . The only difference between two is that the Mandelbrot set is a set of points in complex c -plane starting at z= 0 whereas Julia set is an image for a fixed c value starting nonzero z [17] . A basic Mandelbrot set image and its corresponding various Julia sets are shown in the given figure:

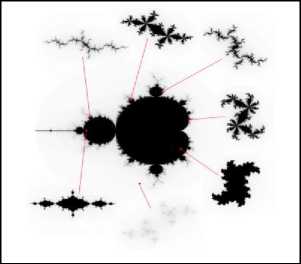
Fig.1. Mandelbrot Set and Its Corresponding Julia Set Images

Mann Iteration: Initially the iteration method is given by W.R. Mann[18]

zn+1 = 5*f(zn) + (1 -5)*zn .        (1)

where z is a complex number and 0 and s are convergent to a non-zero number.

Superior Mandelbrot Set: A Superior Mandelbrot set SM for a function of the form Q c (z) = zⁿ + c, n = 1, 2,..., is defined as the collection of c e C for which the superior orbit of the point 0 is bounded [19],

SM={ c e C : { Q^kk (0): k=0, 1,.....} is bounded in SO}.

Superior Julia Set: The set of complex points SK whose orbits are bounded under superior iteration of a function Q is called the filled superior Julia set. A superior Julia set SJ of Q is the boundary of the filled superior Julia set SK [20].

Ishikawa Iteration [21]: Let X be a subset of real or complex numbers and f:X→X for x₀ ε X , we have the sequences { x_n } and { y_n } in X in the following manner:

y_n = sfKx) + (1 - s)x_n        (2)

* n+ i = s „ f ⁽y „ ) + (1 - SnM        (3)

where 0 < s_n< 1, 0 < s „ < land s „ & s_n are both convergent to a non-zero number.

The sequences x_n and y_n constructed above is called Ishikawa sequences of iterations or Relative Superior sequences of iterates. We denote it by RSO (x₀, s _n, s„ , t) .

Relative Superior Mandelbrot Set: Relative Superior Mandelbrot set RSM for the function of the form Q c (z) = zⁿ + c , where n = 1, 2, 3, 4… is defined as the collection of c ε C for which the orbit of 0 is bounded [22] i.e.

RSM = { c e C : { Q k (0): k =0, 1, .....} is bounded in

RSO}.

Relative Superior Julia Set ： The set of points RSK whose orbits are bounded under relative superior iteration of the function Q(z) is called Relative Superior Julia sets. Relative Superior Julia set of Q is the boundary of Julia set RSK.

Authors in the paper [23] have been analyzed the rate of convergence of superior transcendental Mandelbrot function and concluded that the said fractal function converges very fast to its fixed point. Fractal images exhibit the randomness property, appropriate to design a secure and reliable cryptosystem. Fractal based cryptosystem is designed using a complex number rather than the prime numbers, thus the generation of a private key and a public key is carried out using complex number arithmetic. The chaotic nature of fractal leads to the sensitiveness of the key value towards initial value, makes it difficult to produce accurate key by an intruder. An Additional advantage of using fractal as a key is the key size which generally impacts on the number of guesses that an attacker would need to make in order to find the key e.g. brute force attack i.e. it determines the feasibility of a collision attack. All these sequences make fractal suitable to be used as encryption/decryption key.

• III.    Related Works

In previous traditional techniques, key size depends on the existed prime numbers in the given range. In the case of using the fractal key, the exchange key space depends on the size of the keys, which extend the key space, shrink the key size and make it more complex [24].

A paper described the detail analyses of 27 different encryption algorithms in terms of randomness, speed, entropy, a correlation coefficient between pixels, mean square error, key sensitivity and NIST statistical test. Authors covered image encryption algorithm based on a discrete chaotic map (Arnold’s cat map), a continuous chaotic system (Lorenz) and non-chaotic generators (fractal and chess based system) to explain different angels of effectiveness to secure the data transmission over the highly insecure network. Thus, the algorithm with permutation-substitution phases is more secure than permutation-only and substitution-only encryption algorithm. Later a comparative analysis has been carried out by the authors with 11 encryption algorithms with respect to the used PRNG (pseudo random number generator), algorithm outline, input data and a kind of analysis parameters [25].

A symmetric key stream cryptography algorithm is proposed by the authors in which cipher image incorporates both logistic chaotic map and Tent map. The main feature lies in the use of secret key derived from the biometric images. The encryption of an image is executed pixel by pixel and in an iterative manner. The cipher image relies on the secret key, previous pixel’s encryption information and used logistic chaotic map or Tent map. Authors also carried out the security and performance analysis of given algorithm using histogram analysis, adjacent pixel correlation analysis, Information entropy analysis and key sensitivity analysis [26].

The effectiveness of an image encryption algorithm can be analyzed in terms of parameters like histogram analysis, adjacent pixel correlation analysis, mean value analysis, key space analysis, encryption speed and the number of pixels change rate (NPCR) and unified average changing intensity (UACI) tests. In the given paper, authors conducted all the above-given tests to measure the security and performance issues of an image encryption algorithm using a key image which is a binary image of the same size as of original image [27].

Authors have applied wavelet transform, fractal based encryption key and substitution of pixels through chaos function to design a cryptosystem used in social networking [28]. The advantages of wavelet transform to reduce the image size, consequently minimized the calculation time of proposed method as well. The complexity of the system is enhanced by applying two levels of encryption using fractal and chaos function.

An important tool in image encryption is scrambling deals with change in position of the pixels and helps to minimize the correlation coefficient value. If correlation coefficient between an original image and the encrypted image is zero or near to zero, a hacker will be unable to guess the encryption method or key. The author uses Hilbert curve to scramble the pixel position and then encrypt the image using a secret key derived from the Julia set fractal. The outcome of algorithm analysis proved it highly secure algorithm against the given attacks [29].

The proposed cryptosystem used key based on a fractal image to encrypt the plain image in the paper. The main advantage to using fractal key is its small key storage requirement and robustness to the attack. In the proposed method, to calculate an encryption key, distance parameter δ must be chosen wisely so that algorithm could lead to a secure encrypted image. It must not be so close as well as not extremely large (such as the size of an image). The author also performed PSNR test in the interval ẟ ∈ {20, 120] to test the efficiency of the proposed cryptosystem and concluded that the improved result is possible for ẟ = 1023 [30]․

Mandelbrot set is one of the complex fractals with infinite boundaries. The author utilized the randomness of Mandelbrot set and generated the encryption key using Mandelbrot set and Hilbert curve transformation. A comparative analysis has also been taken with the algorithm given by Rozouvan V. [30]. The range of interval distance r in current experiment is [1, 65025], whereas in the paper [30], it was [0, 254]. PSNR value rapidly increases when r crossed its critical value. In the experiment implemented by Rozouvan, the critical value of r was 150, whereas, Yuan-Yuan Sun et al. achieved a remarkable improvement in the critical value of interval distance r i.e. 40,000 [31].

A novel Image encryption technique using single as well as multi-fractal images is proposed in the paper. The information about source image is hidden in the complex structure of used fractal. It has been noticed from the correlation result that to increase the pixel confusion, a non-linear multiplexing with one-bit delay is required. The result has been analyzed using several standard methods and concluded that the proposed method is secure and efficient [32].

A new approach to encryption using fractal geometry is discussed by the author in which a fractal is generated by using some initial parameters and then use it to encrypt a predetermined length of a message by using fractal orbits to corresponding alphabet mapping [10].

Authors utilized the randomness of fractal function and proposed a pseudo-random number generator using a fractal image. The author investigated three different scenarios i.e. delay block effect, non-linear network effect and delay with non-linear network effect using methods histogram analysis, pixel correlation analysis and NIST results. Later an image encryption process is executed using key sequence generated through the above given method which yielded a promising output [33].

A highly complex and secure algorithm is proposed by the authors which used DWT and multi-chaos for pixel encryption. The process starts with the execution of DWT on the source image and then recombine all matrices to obtain scrambled matrix. On the other side, a secret key is obtained by combining all three sub-chaotic matrices generated with the help of few initial parameters. Perform BitXOR operation and got an encrypted image. Statistical analysis showed an improved key space, high key sensitive and ability to resist attacks [34].

The author Himan Khanzadi et al. proposed an image encryption method based on the random bit sequence generator using chaotic logistic map and Tent map. The whole algorithm executed major five steps i.e. pixel permutation, pixel decomposition, bit map permutation, bit map substitution, and bit map composition. The source image pixels are permuted and substituted as per a random bit and random number matrix. The given method is evaluated using chi-square test with standard approaches [35].

The paper described a stream cipher encryption algorithm implemented on a compressed image. A fractal dictionary encoding method is used in the image compression to achieve good quality image reconstruction. This is followed by a data pre-processing step before performing actual encryption on the plain text. To introduce a perturbation in the stream cipher, diffusion is realized to a certain extent [36].

The authors derived an encryption key from the chaotic function such as logistic mapping and Hannon mapping. Encryption is achieved by applying fractal based encryption key to the source image [37].

The proposed algorithm is an improved idea of modulo based image encryption given by Rozouvan [30]. The author suggests an inclusion of chaotic map as additional step to achieve better security. Here Arnold cat map is used to perform pixels shuffling before pixel encryption to complicate the attack complexity [38].

Key exchange is a method used in a public key cryptographic system, in which sender and receiver exchanged secret key or few parameters over a public channel. In 2007, Alia and Samsudin proposed a key exchange protocol utilized the intrinsic relationship between Mandelbrot set and Julia set [3].

Authors utilized the same concept of key exchange between the sender and receiver and generated private key secretly. Following this process by creating cipher text at sender side using Juliafn with input parameters k and d . After receiving cipher text, the receiver also used the same Juliafn with input parameter n and e and decrypt the message to the original. A detailed comparative analysis is carried out by the authors to depict the importance of recent fractal based cryptosystem over traditional RSA based cryptosystem [4].

Generally, encryption algorithms can be classified into three categories, namely (i) symmetric cryptography (ii)

asymmetric cryptography (iii) hash function. A detailed comparative analysis has been done for the given four cryptographic algorithms; these are AES, DES, TripleDES and Blowfish. The behavioural study is carried out of all above mentioned algorithm when implementing in a single system with a maximum file size of 2547kb [39].

The author highlighted about the basic structure of Mandelbrot set and related Julia set in the paper. It also explores the implementation process of a fractal set and its optimization. The fractal function can be used in various applications such as graphics, medical imaging, cryptography, astronomy, telecommunication and much more. A brief example of fractal cryptography using key exchange protocol is given at the end [40].

An efficient encryption algorithm based on pixel shuffling is proposed by the author. The method works only on the displacement of RGB pixels, therefore, no change occurs in the size of an image during encryption/decryption phase [41].

A concept of the hybrid hyper chaotic sequence is generated using hyper chaotic system. The chaotic key generation in the proposed algorithm is done in two steps. An initial chaotic key stream is derived using the obtained hybrid hyper chaotic sequence which is gone through two rounds of diffusion operation on an initial key and plain image to become an encryption key stream. [42].

A paper explored and examined a wide range of efficient image encryption techniques. This whole paper is ordered in the premise of full image encryption and partial image encryption under spatial, domain and hybrid categories. According to the survey report, full image encryption methods are time consuming but comparatively provide secure state of an encoded system. Partial encryption is suggested for some constant application that adjusts security with procedure execution time [43].

• IV.    Proposed Algorithm

This section describes the proposed encryption system in detail with the help of a working example. As mentioned in the previous section, the given algorithm works for Mann iterated fractal function as well as for Ishikawa iterated fractal function.

• A.    Encryption and Decryption Process

The process starts with some initial values by which a public key is to be generated on both sides using iterated Mandelbrot function. Public keys can be seen and accessed by any unauthorized person so no security concern arises while transmitting the key. Both sides transmit their respective public key to the other side. In next step generate a shared private key using Iterated Julia function which required global parameters, private parameters and received public key on both sides. Common key on both sides leads no need to transmit the private key over the public channel. Encrypt the required data using the generated encryption (shared) key and transmit cipher text to the receiver.

At the receiver side, a receiver used its private (shared) key which is same as sender, to decrypt the cipher text and got the original text.

In the paper, I have applied two Iterated fractal functions i.e. superior fractal function (Mann Iterated) and relative superior fractal function (Ishikawa iterated). Accordingly, a superior fractal function generates the encryption key using two complex functions whereas relative superior fractal function uses three complex functions to generate a symmetric key.

• B.    Detailed Algorithm Process Flow

The key generation process starts with the assumption of few parameters such as c and s as global variables known publicly, n and e as private variables known to the sender and k and d as private variables known to the receiver only. A Mann iterated Mandelbrot function is used by the sender and receiver to generate their corresponding public key i.e. zne and zkd which will be transmitted to the other side. The used superior Mandelbrot set function “supMS” is:

Sender Side f (zn ) = zn * c * e; c, z, e C Z and z0 = c (4)

Receiver Side f (zn) = zn * c * d; c, z, d C Z and z0 = c    (5)

Common to both sides zn+1 = 5 * f(zn ) + (1 - 5)* zn where 0

Sender received public key zkd from the receiver and used it to generate its private key znekd using superior Julia function “supJS”. The generated private key is impossible to regenerate by the intruder, since the values n and e are unknown to the public. In the same way, receiver generated its private key zkdne with the help of variables k and d known to the receiver only and the public key i.e. zne of the sender. The used “supJS” function is:

Sender Side f ( zn) = zn * c * e; c, z, e C Z and z0 = zkd(7)

Receiver Side f (zn) = zn * c * d; c, z, d C Z and z0 = zne(8)

Common on both sides zn+1 = s* f (zn) + (1 -s)*zn , where 0

After generating shared keys, the sender uses its private key to encrypt the data and transmit it to the receiver. At the receiving end, the receiver has its own private key which is same as the sender’s private key to decrypt the received data.

In the above given approach, a fractal based encryption key is generated using one step feedback process i.e. Mann iterated fractal function. In the next, a shared key is generated using two step feedback process i.e. Ishikawa iterated fractal function which is more complex process than the previous one, hence more secure and invulnerable by the hacker.

The used relative superior Mandelbrot function Rel_supMS function:

Sender Side f (zn ) = zn * c * e; c, z, e C Z and z0 = c (10)

Receiver Side f (zn) = zn * c * d; c, z, d C Z and z0 = c (11)

Common to both sides

У п = S i * f⁽Z n ) + ⁽1 - sj * z n         (12)

z n+i = S*f⁽y n ⁾ + (1-S⁾*z n         (13)

where 0< s <1 and 0< s₁ <1

The algorithm works in the same way as before except one addition iteration function. Both parties would be able to generate their public key using the above Rel_supMS function. In subsequent steps, to generate private keys, relative superior Julia function i.e. Rel_supJS will be used. The function is:

Sender Side f (zn ) = zn * c * e; c, z, e C Z and z0 = zkd (14)

Receiver Side f (zn) = zn * c * d; c, z, d C Z and z0 = zne (15)

Common to both sides

У п = S i * /(Z n ) + ⁽1 - S i ) * z n         (16)

z n+ i = S */⁽У п ⁾ + ⁽1 -s) *z n        (17)

where 0

The remaining process to get decrypted text transmitted from sender side in cipher form is same as previous one. The connection between Mandelbrot set and Julia set makes it possible to produce the shared key which does not need to be transmitted over the network, hence inaccessible to the illegal users.

Sender Side

Receiver Side

Input parameters c,s (global) and n,e (private)

• •    Apply supMS fractal function

• •    Generate Public key (zne)

  Input parameters c,s (global) and k,d (private)

  
  

  • •    Apply supMS fractal function

  • •    Generate Public key (zkd)

  
  

Fig.2. Process to Create Sender’s And Receiver’s Public Key

After completing the above process, both parties exchanged their corresponding public key and further generate a common shared key (private key) at their own site.

Sender Side:

Receiver's public key (zkd) and sender's input parameters

• 1.    Apply supJS to generate private key (znekd)

• 2.    Encrypt given text using znekd and transmit it to receiver

Receiver Side:

Sender's public key (zne) and receiver's input parameters

• 1.    Apply supJS to generate private key (zkdne)

• 2.    Decrypt received cipher text using zkdne

  
  
  

Fig.3. Encryption and Decryption Process

• V. Simulation Result and Performance Analysis

This section provides a working example and a detailed performance analysis in terms of key space, key sensitivity and execution time of various phases of the proposed algorithm. The method used an iterated fractal function which works on complex numbers. In the given example, the impact of iterated fractal function will be ignored if the value of s is assumed to be 1.

• A.    A Simple Example

  The working example of both described methods is depicted in the given table. Here we used c = 0.325 + 1.5125i and s= 0.6 as global values used by both parties i.e. sender as well as receiver. Whereas n= 4 and e= 0.015923-0.03179523i are private values of sender and k =3 and d= -0.05124761 + 0.12937622i are private values of receiver kept secretly on respective sites.

The process starts with the calculation of corresponding public keys zne and zkd using supMS by the sender as well the receiver and exchanging it over the network.

After receiving a public key, sender calculated its shared key znekd using supJS function with its parameter values and receiver’s public key. Similarly, receiver calculated its shared key zkdne using the same function with its parameter values and sender’s public key as an input parameter.

To encrypt the required text, sender used its private key znekd and transmit it to the receiver.

At the receiver end, the original text is recovered by decrypting the cipher text using receiver’s private (decryption) key which is same as an encryption key.

The same algorithm is applied to achieve a more secure and complex cryptosystem by using Rel_supMS function and Rel_supJS function to generate a public key and a private (shared) key respectively for both communicating sites. The results are obtained by implementing the proposed algorithm on Matlab R2016b and given in the tables below.

Table 1. Example of Cryptography Algorithm using Mann Iterated Fractal Function

S.No	Description	Sender	Receiver
1.	Initial Values	c=    0.325    + 1.5125i,    s=0.6, e=0.015923-0.03179523i, n=4	c= 0.325 + 1.5125i, s=0.6, d=-0.05124761 + 0.12937622i, k=3
2.	Calculation of public key using supMS function	0.0072687838200 128062515     + 0.0534070804687 6657438i	0.013623278151994 241209         + 0.028539520494632 282292i
3.	Calculation of shared   key using  supJS function (128bit)	0.0003973801569 314…+ 0.0010276603998 63009…i	0.000397380156931 4…+ 0.001027660399863 009…i
4.	Output	Encrypted   Text: sample-“collection     of special characters…”	Original        text: sample- hi,this is an encryption algorithm…

Table 2. Example of Cryptography Algorithm using Ishikawa Iterated Fractal Function

S.No .	Description	Sender	Receiver
1.	Initial Values	c= 0.325 + 1.5125i, s=0.6, e=0.015923-0.03179523i, n=4, s1=	c= 0.325 + 1.5125i, s=0.6, d=-0.05124761 + 0.12937622i, k=3
2.	Calculation of public key using Rel_supMS function	0.007615794477461 3855132 + 0.048888281039250 120115i	0.0160878757964 03804623      + 0.0475428125672 6007264i
3.	Calculation of shared key using Rel_supJS function (128bit)	0.000426887227059 23169…+ 0.001547439851460 837…i	0.0004268872270 5923169… + 0.0015474398514 60837…i
4.	Output	Encrypted    Text: sample-“collection of            special characters…”	Original text: sample- hi,this is an encryption algorithm…

• B.    Key Space

  Key space refers to the total possible combinations of a given key. To secure the data from brute force attack, key space must be large enough. In the proposed algorithm, a 128 bits’ key is generated using Matlab’s variable precision arithmetic to encrypt the given data, so the possible number of keys will be 2¹²⁸. This much of key combinations are not practically possible to decode, hence provides a reliable cryptosystem in terms of key space.

• C.    Key Sensitivity Analysis

  The fractal structure exhibits chaotic behaviour which indicates a drastic change in output in case of a minor change in input. This property is also known as the butterfly effect. In the given method, a 128 bits’ key is used to encrypt/decrypt the given text. Suppose in long format, the key value is 0.000426887227059 + 0.001547439851461i; To test the sensitivity of the key make a slight change in the value of key i.e. 0.000426887227069 + 0.001547439851460i and you will get a different decrypted text instead of expected original text from the method. It depicts that a tiny change in the key value will produce a great difference in the output, so it concludes that the key is highly sensitive.

• D.    Time Analysis

  The running time of an algorithm is an important concern in performance measurement. A public key generation, private key generation and encryption/decryption process time are measured for the proposed algorithm in case of a 64bit key as well as for 128bit key encrypting/decrypting a text file. The time analysis is carried out on Intel® Atom™ x7-z8700 CPU @1.60GHz with 4 GB RAM. The result is shown in table 3:

Table 3. Execution Time of Various Processes

Process	Bit Size	Mann Iterated Fractal Function (seconds)	Ishikawa Iterated Fractal Function (seconds)
Public Key Generation (Sender)	64 Bit	0.105	0.140
Private          Key Generation (Sender)		0.111	0.148
Encryption		0.404	0.413
Public Key Generation (Receiver)		0.076	0.103
Private          Key Generation (Receiver)		0.083	0.109
Decryption		0.087	0.092
Public Key Generation (Sender)	128 Bit	0.105	0.140
Private          Key Generation (Sender)		0.115	0.154
Encryption		0.405	0.407
Public Key Generation (Receiver)		0.076	0.103
Private          Key Generation (Receiver)		0.080	0.105
Decryption		0.087	0.089

• VI. Conclusion

In this paper, an encryption algorithm based on Mann iterated and Ishikawa iterated fractal function is proposed. This approach provides a much complex process for generating the encryption key using iterated Mandelbrot and Julia set. The fact is that the key generation required few isolated parameters kept secretly to the site itself leads to a secure cryptosystem. The chaotic nature of the fractal function and a large size encryption key makes its invulnerable to brute force attack commonly known decoding threat. The performance analysis shows that moreover both methods executed at the same time so better use more complex key generation method i.e. relative superior fractal sets. The given algorithm has high sensitivity to initial parameters, in that case, a small variation in parameter value will change its decrypted message completely. As a resultant, the proposed provides a secure and reliable cryptosystem to meet today’s challenging application requirements.