Сжатие света в двухатомной модели Джейнса-Каммингса с невырожденными двухфотонными переходами

Одним из наиболее перспективных направлений в современной квантовой оптике является исследование сжатых состояний электромагнитного поля. Явление сжатия света изучено в настоящее время как теоретически, так и экспериментально в огромном количестве работ (см. ссылки в обзорах и монографиях [1],[2]). Такие состояния привлекают особое внимание не только потому, что они позволяют глубже понять природу электромагнитного поля, но и благодаря их широким возможным применениям для высокоточных оптических измерений, оптической связи, квантовых вычислений и др. [2]. Экспериментально сжатие света было впервые реализовано в 1985 году в нелинейном процессе четырехволнового смешения света в оптическом резонаторе [3]. Позднее для генерации сжатых состояний электромагнитного поля использовались различные нелинейные оптические процессы. В настоящее время выполнено более 40 различных экспериментов по наблюдению сжатых состояний света в различных нелинейных оптических средах, в том числе для пучков атомов в резонаторах [1]. Для атомов в резонаторах эксперименты по генерации сжатого света в настоящее время выполнены только для случая высоких плотностей атомов. При наличии точного резонанса моды резонаторного поля с атомным переходом такая система атомов представляет собой сильно нелинейную среду, в которой возможна генерация сжатого света, регистрируемого экспериментально. Имеются две группы экспериментов по наблюдению сжатых состояний света для пучков атомов в резонаторе. В эксперименте Орозко с соавторами [4] использовались плотные пучки атомов Na, а в эксперименте X. Бэчера с соавторами [5] использовались атомные пучки Ba, создающие оптически тонкие слои атомов в резонаторе. В обоих экспериментах не удалось добиться заметного практически значимого подавления шума (уменьшение уровня шума для резонаторного поля составило примерно 20 %). При этом авторам не удалось проинтерпретировать результаты экспериментов в рамках обычной полуклассической модели нелинейной среды, основанной на уравнениях Максвелла-Блоха [6]. Таким образом, для адекватного описания особенностей атом-полевого взаимодействия в реализованных экс- периментах необходим полный анализ квантовой динамики атомной и полевой подсистем. Хорошо известно, что простейшей нетривиальной моделью, позволяющей описать квантовые эффекты излучения атома в резонаторе, является модель Джейнса-Каммингса, описывающая двухуровневый атом, взаимодействующий с выделенной модой квантованного электромагнитного поля в идеальном резонаторе. В рамках этой модели и ее простейших обобщений, учитывающих наличие дополнительного третьего атомного уровня, многофотонных переходов, многомодовости квантового электромагнитного поля и второго двух- или трехуровневого атома, как оказалось, могут быть описаны практически все основные квантовые эффекты, возникающие при взаимодействии излучения с веществом, в том числе и сжатие света [7]. В настоящее время интерес к таким моделям перестал быть чисто теоретическим, поскольку реализация одноатомного однофотонного и двухфотонного мазера и микролазера [8],[9] предоставила возможность непосредственного исследования таких систем и экспериментальной проверки основных положений квантовой электродинамики. Модель Джейнса-Каммингса с диссипацией была реализована также на ионах в магнитных ловушках, квантовых точках и в сверхпроводящих системах [2]. Для единичных ионов в магнитных ловушках Пауля наблюдалась генерация колебательных сжатых состояний ионов [10].

Возможность сжатия света в модели Джейнса-Каммингса и ее простейших обобщениях анализировалась многими авторами, начиная с работы П. Мейстре и М. Зубайри [11]. Многочисленные ссылки на последующие работы можно найти в обзоре [12] и монографии [1]. Для описания результатов экспериментов по генерации сжатого света пучками атомов в резонаторах [4],[5] естественно рассмотреть многоатомную модель Джейнса-Каммингса. При этом точные решения для временного поведения наблюдаемого поля могут быть получены только в простейшем случае двухатомных систем. Сжатие света в простейшей системе двух двухуровневых атомов с различными типами переходов в идеальном резонаторе в случае вакуумного, коге- рентного и теплового состояний резонаторного поля было рассмотрено в работах [13]-[16]. При этом для случая, когда в атомах разрешены однофотонные переходы, максимальная степень сжатия для двухатомной модели составляет около 20 %, что находится в согласии с экспериментальными результатами. В настоящее время особое внимание в квантовой оптике и квантовой информатике уделяется многофотонным процессам ввиду высокой степени корреляции испускаемых атомами фотонов [17]. Представляет большой интерес исследовать особенности сжатия света в двухатомной модели Джейнса-Каммингса с невырожденными двухфотонными переходами, так как наличие сильной корреляции между фотонами должно приводить к усилению степени сжатия резонаторного поля. Сжатие света в многофотонной двухатомной модели рассматривалось ранее в [13], [14]. Однако авторы ограничились рассмотрением случая вакуумного или слабого когерентного начального состояния поля (среднее начальное число фотонов в моде n << 1), в то время как в указанных выше экспериментах выполнялось противоположное условие n >> 1.

В настоящей работе нами детально исследованы особенности сжатия света в вырожденной двухфотонной двухатомной модели Джейнса-Каммингса для различных начальных интенсивностей резонаторного поля и различных начальных состояний атомной подсистемы. Заметим, что аналогичное исследование для невырожденной двухфотонной модели проведено нами в работе [18].

Рассмотрим систему двух двухуровневых атомов с частотой атомного перехода ® ₀, взаимодействующих с модой квантового когерентного электромагнитного поля частоты ® посредством двухфотонных невырожденных переходов. Предположим также наличие в системе двухфотонного резонанса ® ₀ = 2 ® . Тогда гамильтониан изучаемой системы в приближении вращающейся волны можно записать в виде

H = h ® a ⁺ a + ^ й ® ₀ R j + ^ й g ( R*а ² + R - a ^{+ 2}), (1) j = 1 j = 1

где а ⁺ ( а ) - оператор рождения (уничтожения) фотона резонаторной моды, R j - оператор полуразности населенностей в j -ом двухуровневом атоме, R + ( R - ) - повышающий (понижающий) оператор в j -ом двухуровневом атоме и д - константа атом-фотонного взаимодействия. Обозначим через | +) и | -) возбужденное и основное состояния одиночного атома, а через | n ) фоковское состояние моды резонаторного поля. Тогда двухатомная волновая функция есть | v 1 , v ₂ ) = | v 1 ) | v ₂ ) , где v = +, -.

Пусть атомы приготовлены в начальный момент в произвольной чистой суперпозиции базисных векторов

I ^ ⁽⁰⁾) = ^а\ ⁺ , +) ⁺ Р\ ⁺ , ^-) ⁺ У I ^- , ⁺ ) ^{+ 8} | ^- , ^-) , где а , в , у , 8 - произвольные комплексные числа, удовлетворяющие условию нормировки, а резонаторное поле в когерентном состоянии га

I и) = £ F n | n ) . n = 0

— n / 2

Здесь F_n = exp ( - n / 2) nt=e ^Ф , где n - среднее V n !

число фотонов в моде, а ф - фаза когерентного состояния.

Точное решение временного уравнения Шредингера для модели с гамильтонианом (1) и при выбранных начальных условиях имеет вид

| Т( t )) = £ ( A_n ( t )| + , +) ” + B n ( t )| + , - | n + 2) + n

+Cn I-,+ I” + 2 + Dn I-, — |n + 4),

где

A n ⁽ t ) = 2 ® ^{; (} P ” ⁺ q n ^{COs[2 Q} n t ^{]) а} F n ^-

-      sin[2 Q ” t ]( в + у ) F ” + 2 - p^ sin² [ Q „ t ] 8 F ” + 4 ,

2Q n                    Q ”

B n ( t ) = -      sin[2 Q ” t ] a F ” + (cos²[ Q „ t ] 0 -

^{2 Q} n

- sin²[ Q ” t ] y ) F ” + 2 - 2 Q- sin[2 Q „ t ] 8 F ” + 4 ,

C n =- -pp - sin[2 Q ” t ] a F ” + (cos²[ Q „ t ] y- ^{2 Q} n

- sin²[ Q ” t ] P ) F ” + 2 - 2 Q- sin[2 Q ” t ] 8 F ” + 4 ,

D n

p„q„ sin2[Q”t]     _

Q²     “ F ”

^Q n

^{iP n}      ” t ^] CM C n + 2 +

^{2 Q} n

( q ” + p ” cos[2 Q ”t ])

2Q ² n

8 F n + 4 ,

где

qn = V(n +1)(n + 2), Pn = 4(” + 3)(” + 4), и Qn = V (p” + q”)/ 2 - частоты Раби.

Для того чтобы исследовать возможность сжатия моды поля введем стандартным образом медленно-меняющиеся квадратурные компоненты для моды резонаторного поля

X 1 = ( 1/2 ) ( ae ^гт * + a ⁺ e ^-гт * ) ,

X ₂ = ( 1/2 i ) ( ae ^гт * - a ⁺ e ^-гт * ) .

Поскольку квадратурные компоненты удовлетворяю коммутационному соотношению [ X ₁ , X ₂ ] = г / 2 , соотношение неопределенностей для них принимает вид

(AX,)2(AX2)2 > 1/16, где (AXi )2 = 2 (i = 1,2) - дисперсии квадратурных компонент. Как известно, сжатое состояние минимизирует соотношение неопределенностей для квадратурных компонент. При этом для одной из компонент (сжатой) выполняется соотношение (AXi )2 < 1/4 (i = 1,2). Для анализа численных расчетов удобно ввести так называемые параметры сжатия следующим образом

( A X ,)²) - 1 / 4            2

S, =---- i ---------= 4 (A X ) - 1 ( i = 1 , 2) .

1 / 4

Условие S i <  0 для какой-либо из квадратурных компонент будет означать наличие в ней уменьшения флуктуаций поля ниже квантового предела. Значению S i = - 1 . соответствует полное отсутствие квантовых флуктуаций в соответствующей квадратурной компоненте. Часто в качестве критерия сжатия используют также величину | S i | Х 100 %. Тогда 100% сжатию соответствует нулевая неопределенность одной из компонент. В терминах операторов рождения и уничтожения фотонов параметры сжатия можно представить в виде

S 1 = 2 < a ⁺ a ) + 2 Re <  a ² e ^{2 1Ю} t ) - 4( Re <  ae ^1Ю t »² , (3)

S ₂ = 2 < a ⁺ a ) - 2 Re <  a ² e ^{2 1Ю} t ) - 4(Im < ae ^1Ю t »². (4)

Используя явное выражение для волновой функции (2) нетрудно вычислить явные временные зависимости параметров сжатия, определяемые формулами (3) и (4). Указанные соотношения не приведены из-за их слишком громоздкого вида. Результаты численного моделирования временной зависимости параметров сжатия для различных значений параметров модели приведены на рис. 1-3.

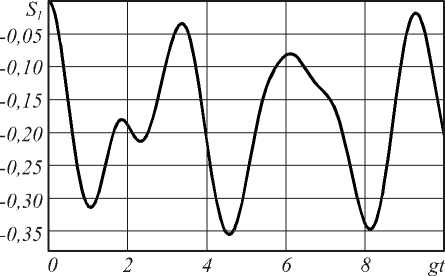
Рис. 1. Длинновременное поведение параметра сжатия S₁ для модели с n = 0,2 . Атомы в начальный момент времени находятся в состоянии | - , -) .

На рис. 1 показано длинновременное поведение параметра сжатия в первой квадратурной компоненте для малых значений начальной интенсивности резонаторного поля и атомов, приготовленных в начальный момент времени в основном состоянии | - , -) .

Из рисунка видно, что для малых начальных интенсивностей поля параметр сжатия S 1 принимает для любых моментов времени отрицательное значение, это говорит о стационарном характере сжатия в первой квадратурной компоненте. Естественно, что при этом в любой момент времени S 2 > 0 , т.е. во второй квадратурной компоненте сжатие отсутствует при любых начальных интенсивностях резонаторного поля. Такое поведение модели заметно отличается от поведения двухатомной однофотонной модели, для которой при выбранных начальных интенсивностях поля параметры сжатия S 1 и S 2 осциллируют во времени, принимая как положительные, так и отрицательные значения.

При этом максимальная степень сжатия составляет около 20%. При увеличении начальной интенсивности поля число пиков для параметра сжатия S 1 в области отрицательных значений сжатие уменьшается (при условии n >  1,5 остается всего один пик в отрицательной области). При этом максимальная степень сжатия в первой квадратурной компоненте в области первого пика достигает 60% в случае n = 1,5 (см. рис.2).

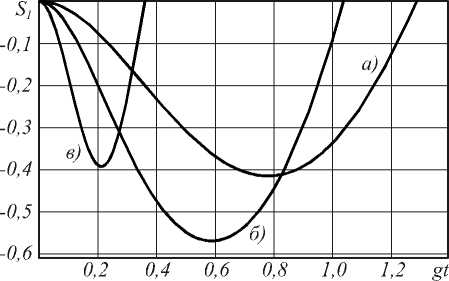
Рис. 2. Коротковременное поведение параметра сжатия S 1 для модели с: a) n = 0,5 б) n = 1,5 в) n = 5 . Атомы в начальный момент времени находятся в состоянии

I - , -> .

Таким образом, максимальная степень сжатия в двухфотонной модели почти в три раза превосходит соответствующую величину для однофотонной модели, исследованной в [14-17]. На рис. 3 показано коротковременное поведение параметра сжатия S 1 в случае возбужденного начального состояния атомов. Максимальная степень сжатия в первой квадратурной компоненте составляет около 40% и достигается для среднего числа фотонов n = 15 . При этом сжатие в первой квадратурной компоненте возникает с запаздыванием во времени. Интересно отметить, что в случае однофотонных переходов сжатие в первой квадратурной компоненте возникает только в случае, когда атомы первоначально приготовлены в основном состоянии [14,15]. Для двухфотонного случая, как показывает численное моделирование, сжатие возможно при любом начальном состоянии атомов.

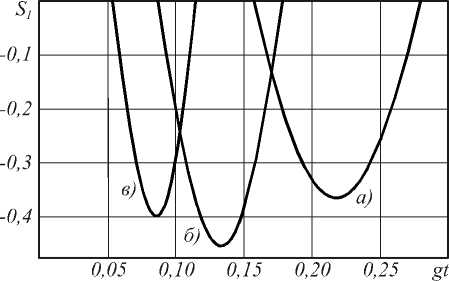
Рис. 3. Коротковременное поведение параметра сжатия S i для модели с: a) n = 8 б) n = 15 в) n = 25 . Атомы в начальный момент времени находятся в основном состоянии I ⁺ , +)

Таким образом, в настоящей работе мы детально исследовали особенности сжатия света в системе двух атомов с вырожденными двухфотонными переходами, взаимодействующих с модой когерентного поля в резонаторе без потерь. При этом было показано, что такая нелинейная среда является значительно более выгодной для генерации сжатого света в сравнении с системой атомов, в которой разрешены однофотонные переходы. Поэтому представляло бы интерес проведение эксперимента по наблюдению сжатого света для систем атомов в резонаторе с использованием двухфотонных переходов.