Сжато-изогнутые стержни, жестко закрепленные в основании, предварительно напряженные комбинированным способом

Постановка задачи

Предварительное напряжение сжато-изогнутых стержней комбинированным способом заключается в равномерной вытяжке тонкой стенки двутавра с последующим присоединением к ней поясных листов по схеме (рис. 1). Согласно этой методике моменты усилий предварительного напряжения M0 будут создавать в стержнях колонн прогибы, ориентированные различным образом относительно оси стержня и, следовательно, предварительные нормальные напряжения, вектор которых направлен сторону, противоположную вектору соответствующих напряжений от внешней нагрузки.

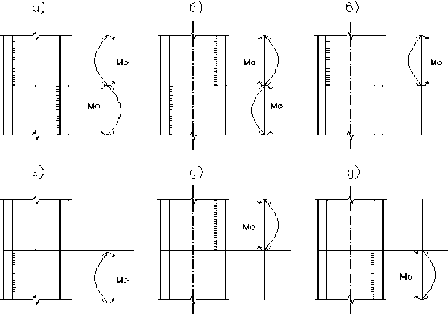
Рис.1. Возможные варианты предварительного напряжения стержней

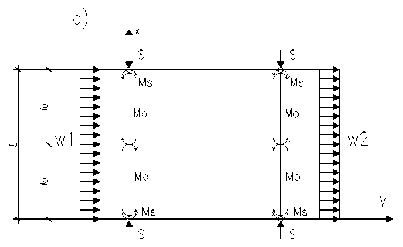
Рис.2. Схема нагружения рамы на основе предварительно напряженных стержней

Колонны на основе стержней предварительно напряженных комбинированным способом в рамах зданий промышленного или административного назначения могут находиться под воздействием различных нагрузок.

Возможный вариант нагружения однопролетной рамы представлен на рисунке 2.

Напряженно-деформированное состояние внецентреннонагруженных предварительно напряженных стержней

В основу исследования положен принцип независимости действия сил. На основании этого принципа сложное нагружение искривленной предварительно напряженной колонны рассмотрим как сумму нагружений прямолинейного стержня, нагруженного внешними сжимающим усилием S и моментом M_s , действующими на стержень одновременно (рис. 3б); прямолинейного стержня, нагруженного ветровой нагрузкой w₁ и сжимающим усилием S (рис.3д); прямолинейного стержня, находящегося под воздействием опорных моментов M_op и M_op1 , возникающих в нижнем жестком узле от моментов M_S и M _w , действующих одновременно с усилием S (рис. 3г, е).

Как указано выше, усилия предварительного напряжения искривляют ось стержня по синусоидальной кривой таким образом, что в средине его наблюдается перегиб оси стержня. Это дает нам право предполагать, что в месте перегиба поворот сечения отсутствует, и, следовательно, здесь имеет место его условно жесткое закрепление.

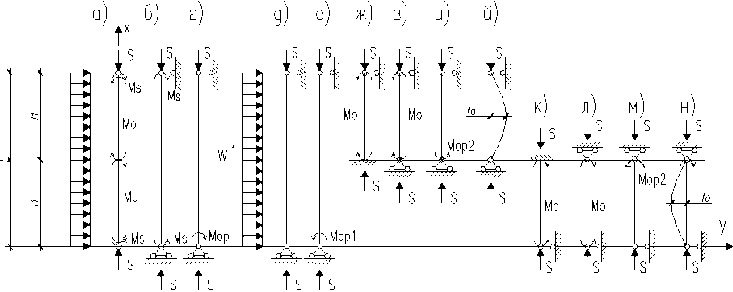
Рис.3. Расчетная схема предварительно напряженной колонны

Исходя из этого предположения расчленим стержень на два условно отправочных элемента, каждый из которых нагрузим моментом усилий предварительного напряжения по схеме (рис. 3ж, к). При этом будем считать, что отправочные элементы в условно жестких узлах будут нагружены опорными моментами Mop1 (рис. 3и, м); кроме этого, в каждом отправочном элементе, находящемся под воздействием сжимающего усилия S и момента усилий предварительного напряжения Mо, будет появляться дополнительный момент внешних нагрузок Mf = Sf0 (f о — выгиб отпра- вочного элемента от момента M0) (рис. 3й, н).

Прогиб стержня с предварительным напряжением в верхней зоне стержня будет иметь вид:

Z y = ^{( — y}S + y op ) + ⁽ y w ^— y opl ) + ⁽ y mo ^— y op 2 + y f )                     ⁽¹⁾

Прогиб стержня, у которого предварительное напряжение осуществляется в нижней зоне:

Z y = ^(-y S + y op ) + ⁽ y w ^- y opl ) ^{- (} y mo ^- y op 2 + y f ),                   (2)

где ys =

—

M s [Sin px + sin p ( L

—

x )

—

x

—

L

—

x

S

sin pL

L

L

];

M

y op =

op [Sin p ( L — x ) L — x

—

S

sin pL

L

];

w cos p ( L 12 — x )

—

У w Sp ² cos pL 12

1] — w ( xL — x ²)};

y op 1 =

y mo

M op 1 _rsin p ( L — x )   L — x

---ё ^[----^:---- т---т —^];

S sin pL L

M_o sin px 1 + sin p ( l — x 1 ) l l — x 1

--------[-----

S

— -- —

sin pl

^x 1

l

■ ];

y op 2

M op 2

S

[

sin p ( l — x i ) l — x i ----------- — ----

sin pl

l

];

S y f = о   f o

Scr sin nx 1

p = д/SI EI x = 2u IL; x — текущая ордината прямолинейного стержня; xi — текущая ордината отправочного элемента, отсчитываемая от середины стержня до узлов закрепления его в основании и верхней шаровой опоре.

Особо обратим внимание на то, что для удобства решения задачи о напряженно-деформированном состоянии предварительно напряженного стержня (рис.За) выражение прогибов разделено на три блока; первый и второй — прогибы, характеризующие деформированное состояние прямого стержня, нагруженного по схеме рисунка Зб-е; третий - прогибы верхнего отправочного элемента, нагруженного по схеме рисунка Зж-й или прогибы нижнего отправочного элемента, нагруженного по схеме рисунка Зк-н.

На первом этапе исследования напряженно-деформированного состояния стержня, предварительно напряженного комбинированным способом, изучим состояние, когда он нагружен только внешними нагрузками, т.е. моментом Mg и равномерно распределенной нагрузкой W1, ими- тирующей ветровое воздействие.

Поворот поперечного сечения прямолинейного стержня, находящегося под воздействием внешних нагрузок по схеме (рис. Зб-д), имеет вид:

dy =   M_s cos px — cos p ( L — x )    M op _pcos p ( L — x )    1

dx     S p       sin pL            S   p sin pL     pL

₊ { w [1 _— ^{(sin ( L 12 — x} ) ]} Sp cos pL 12

^M op 1     _rsrn( L — x )    1

-— p [ —-------

S        sin pL pL

(З)

Поскольку в жестом узле сопряжения стержня с фундаментом поворот поперечного сечения отсутствует, то, приравняв нулю зависимость (3), найдем аналитическое выражение опорных мо ментов M op, M op1.:

^M op = ^M op

»      (1 — cos 2 u )      _

— M op 1 = M s --------1-----1--M sin 2 u (--- tg 2 u 2 u)

2     ( u - tgu )

. ---------------. -------------------------------------------------------------

2         1         1

u (—---^L)

tg 2 u 2 u

= A_o M_s - A 01 M

где A _o , A _o1 — коэффициенты при моментах M s , M w .

В том случае, когда параметр u ^ 0, что означает практическое отсутствие сжимающей нагрузки S = 4u 2EI x IL2,   Mop = 1,5 • Ms - M w.

Значения коэффициентов A _o , A ₀₁ , зависящие от параметра u, представлены в таблицах 1, 2.

Коэффициент A _o

Таблица 1

u	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,9
A o	-1,5	-1,5	-1,5	-1,51	-1,52	-1,54	-1,55	-1,59

Продолжение таблицы 1

u	1,0	1,1	1,2	1,3	1,4	1,5
A o	-1,63	-1,66	-1,7	-1,76	-1,83	-20,

Таблица 2

Коэффициент A ₀₁

u	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
A 01	1,004	0,994	1,013	1,022	0,947	1,05	1,072	1,096

Продолжение таблицы 2

u	0,9	1,0	1,1	1,2	1,3	1,4	1,5
A 01	1,128	1,164	1,22	1,264	1,328	1,394	1,527

Знаки перед коэффициентами A_o , A ₀₁ следует рассматривать как показатель того, что опорные моменты направлены в сторону, противоположную моментам, вызвавших их.

Момент внешних нагрузок в прямолинейном стержне характеризуется второй производной от выражения прогибов y _S , y_op , y_w , y_{op 1} :

d² У 1 = Ms , dx ² EI x

Mw

⁺ ст—{A 01 ^[

EI x

{[ sin px + sin p ( L sin pL

—

sin p ⁽ L ^— x ) ] + 2 [1

sin pL u ²

] — A o [ ^{sin p ( L — x} ) _]} + sin pL

—

cos p ( L 12 — x ),, ]} .

cos pL / 2

Следующим этапом исследования является изучение влияния предварительного напряжения на параметры несущей способности стержня.

Схема воздействия момента усилий предварительного напряжения M₀ и сжимающего усилия S на верхний отправочный элемент стержня представлена на рисунке 3ж-к. Согласно указанным схемам предварительное напряжение будет создавать в стержне напряжения, противоположные соответствующим напряжениям, вызванным внешними нагрузками.

Расчетная схема верхнего элемента представляет собой стержень, условно жестко закрепленный в месте перегиба оси колонны и шарнирным закреплением в верхнем и нижнем узлах.

Уравнении прогиба y_mo , y_{op 2}, y f соответствующего участка представлено в выражении (2).

При решении задачи об опорном моменте M op 2 в условно жестком узле (x i = 0) следует учесть, что выгиб предварительно напряженного верхнего участка стержня f₀ не оказывает влияния на формирование опорного момента, и следовательно, указанный момент должен быть определен на основании выражения прогибов участка стержня по зависимости

У 3 = ^(-У op2 + y f ) =

—

^M op 2 _[ sin p ( l

S sin pl

—

x 1 ) 1 — x 1 --- — ----

l

^] + S "7

S cr     1

sin nx i / 1

—

4 u ²

I n ^2.

Поскольку сжимающее усилие S = 4u ² EI x I 1 2,  а Эйлерова

критическая сила

Sr= = n2EIY 112, то SISr == 4u2/n2. Примем во внимание cr          x                 cr fo = M 012 /4 EIx .

С учетом изложенного поворот сечений стержня

и то,

что выгиб стержня

dy 3 = dx 1

M op 2 l

2 u • EI x

[ cos p ( 1 — x 1 ) sin pl

X] + M^L pl EI x

•

u ²

П

•

cos n x 1 1 1

1 — 4 u ² I n ² .

На основании последней зависимости опорный момент

2 u ³

^M op 2 = ^M 0-- П

•

(-^ — Г*¹

tg 2 u 2 u

—

----------= M 0 A 02 .

4 и ² / п ² )

Здесь Mо — момент усилий предварительного напряжения hK

Mо - Nоy3 - AwRy "2• к + 2 , где No — растягивающее усилие стенки двутавра; Ry

— расчетное сопротивление материала стен-

ки; h — высота двутавра; K — коэффициент асимметрии двутавра (К=1,0).

Значения коэффициента A₀₂ приведены в таблице 3.

d² y 3 dx ₁ ²

EI x

sin px 1 ⁺ sin p ⁽ l ^— x 1 )            sin p ⁽ l ^— x 1 )

- M 0 {-[-----------—,-----------J + Ao2--:----;---- sinpl                            sin pl

— M 0 • u ²

sin nx 1 / l

1 — 4 и ² / n ²

Таблица 3

Коэффициент A ₀₂

u	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
A 02	-0,0095	-0,004	-0,087	-0,154	-0,248	-0,362	-0,500	-0,673

u	0,9	1,0	1,1	1,2	1,3	1,4	1,5
A 02	-0,878	-1,120	-1,400	-1,750	-2,168	-2,755	-3.370

Приступая к формированию выражения момента в верхнем участке стержня, заметим, что момент усилий предварительного напряжения теперь должен быть учтен:

Для нижнего отправочного элемента предварительно напряженного стержня зависимости (7) и (9) также справедливы, но с обратным знаком.

Окончательные выражения моментов получим алгебраическим сложением выражения (5), характеризующего момент внешних нагрузок прямолинейного стержня с выражениями (9) – моментом усилий предварительного напряжения.

С целью наглядного представления о влиянии предварительного напряжения на распределении моментов по длине стержня рассмотрим стальной симметричный двутавр площадью сечения A - 147,6 см², площадью стенки A w - h w t w - 50 • 0,5 - 25,0 см², момент инерции которого i x - 78709 см⁴ , Усилие, растягивающее стенку на стадии предварительного напряжения стержня, N 0 - A w • R y - 25 • 23 - 575 кН. Момент усилий предварительного напряжения

M0 - N0уз - 4792кН • см (Уз - 8,33 см - расстояние от центра тяжести стенки до центра тяжести тавра, образованного из стенки и анкерного поясного листа, служащего «верхним» поясом двутавра). Сжимающее усилие принимаем равным S - 300kH. Коэффициент и - pl/2 -1 /2 • ^S/EIx , соответствующий принятому сжимающему усилию S , находится из зависимости S - 4и2EIx /12,u - 0,16615. Момент внешних нагрузок Ms - Se - 300• 25 - 7500кН • см (е - эксцентриситет сжимающего усилия, принят равным половине высоты сечения стенки двутавра, e - 25,0 см); опорные моменты - Mop - Ao • Ms - —1,5 • 7500 - —11250kH • см;

M_op 1 - M w • A o 1 - 5324 • 1,0 - 5324kH • см; M_{o p2} - M ₀ • A_{o 2} - 4792 • 0,002 - 9,584kH • см.

Коэффициенты A_o , A_{o 1} , A_{o 2} следует принимать по таблицам 1–3.

Момент ветровой нагрузки M w - wL ² /8 - 5324 кН • см .

Суммарные моменты в характерных сечениях стержня показаны на рисунке 4.

Анализ графиков рисунка 4 позволяет сделать выводы:

• 1.    Предварительные напряжения снижают максимальный момент внешних нагрузок на 15,5 %.

  

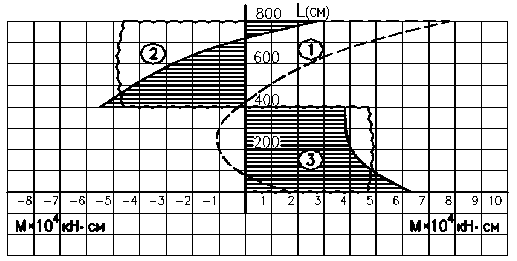
  Рис.4. Распределение моментов внешних нагрузок и усилий предварительного напряжения в двутавровом стальном стержне длиной 7800 мм: 1 - область моментов внешних нагрузок; 2 - область моментов усилий предварительного напряжения стержня; 3 - суммарная эпюра моментов

  
  

• 2.    Предварительное напряжение практически кардинально меняет вектор моментов; моменты распределяются по высоте стержня таким образом, что верхняя часть находится преимущественно под воздействием сжимающих, а нижняя - растягивающих напряжений.

• 3.    Предварительное напряжение приводит к уравновешиванию моментов, что позволяет практически полностью использовать прочностные характеристики материала стержня. Судя по эпюре моментов в нижней области, прочностные характеристики материала стержня будут использоваться на 72,0 %, в верхней области - на 39,0 %, или в среднем по всему стержню - на 55 %. В аналогичном стержне, но без усилий предварительного напряжения прочность стали будет использована всего на 25,3 % (см. область 1, рис.4).

График прогибов стального стержня, предварительно напряженного комбинированным способом с геометрическими параметрами и размерами, принятыми выше, приведен на рисунке 5. Поскольку вектор графика прогибов, вызванных усилиями только внешней нагрузки (кривая 1) направлен в сторону, противоположную соответствующему вектору прогибов от усилий предварительного напряжения (кривая 2), то график суммарного прогиба (кривая 3) свидетельствует о том, что результирующие прогибы предварительно напряженного стержня будут меньше прогибов обычного стержня, с равными геометрическими параметрами и размерами. Последний вывод может быть основанием для утверждения о том, что изгибная жесткость предварительно напряженного стержня выше соответствующей жесткости обычного стержня.

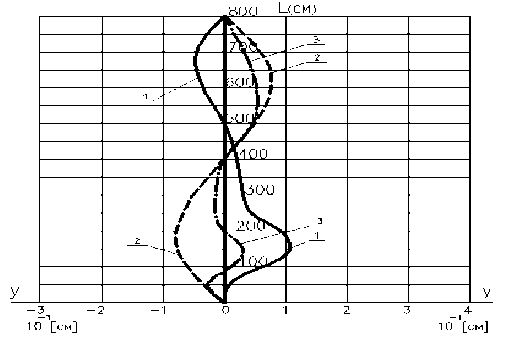
Рис.5. Прогибы предварительно напряженного стержня. 1 - прогиб, вызванный внешней нагрузкой;

2 - то же, от усилий предварительного напряжения; 3 - суммарный прогиб стержня

Следует обратить внимание на то, что численные значения прогибов получены для частного случая. Увеличение внешних нагрузок при детерминированном значении усилий предварительного напряжения будет снижать эффект влияния предварительного напряжения на деформированное состояния стержней, но неизменным останется факт снижения результирующих прогибов исследуемых стержней.

Поперечные усилия Q x , возникающие в стержне от воздействия внешних нагрузок и уси- лий предварительного напряжения в верхней части стержня, определяются дифференцированием трижды уравнения прогибов стержня:

d y EI = Q = M ⋅ xx s dx

2 u _[ cos px - cos p ( L - x )

L         sin pL

] -

+ M

wL 1 sin p ( L / 2 - x )          2 u cos p ( L -

-      ⋅ ⋅                      - M _op ⋅ ⋅

2 u cos pL / 2               L sin pL

2 u cos p ( L - x )           2 u cos p ( l - x ₁ )

^op1 ⋅ L ⋅ sin pL + M ^{op 2} l ⋅ sin pl -

x )

M 2 o u π

l

cos π x ₁ / l

1 - 4 u ² / π ²

Та же самая поперечная сила Q _x в нижней части стержня будет определена при условии, что перед последними тремя членами уравнения (10) знаки будут заменены на противоположные.

Заметим, что формула (10) при отсутствии сжимающего усилия S , что характеризуется стремлением параметра u к нулю, полностью соответствует значениям, известным из курса «Сопротивление материалов». В том случае, когда u ≠ 0 , поперечная нагрузка Qx меняет свои значе- ния.

Влияние предварительного напряжения на величину поперечной нагрузки следует оценивать по двум последним членам выражения (10). В численном выражении это влиян ие зависит от величины сжимающего усилия S = 4 u ² EI_x / l . Чем больше параметр _u = ^{l S} , тем больше 2 EI _x

S и тем существенней исследуемое влияние. При часто встречающихся в процессе эксплуатации однопролетных бескрановых зданий рамного типа нагрузках S = (300 - 400) kH , параметр u ≈ 0,13...0,14 . Сумма двух последних членов зависимости (10)

M o A

2 u

02 l ⋅

sin 2 u

M

+ ⁰ u ² π l

1 - 4 u ²/ π ²

О 27 = 9584 ⋅ 0,0087 ⋅ ^0,27 590

0,26673

+ ⁹⁵⁸⁴ ⋅ 0,018225 ⋅ 3,14 ⋅ 1,007455 = 0,143 + 0,93 = 1,0726 kH .

Внешняя нагрузка – момент Ms = 7500kH ⋅ см и ветровое воздействие

w = 0,07 kH / см при тех же значениях параметра u создают поперечную нагрузку

Q _x = 34,0 kH . В верхнем шарнирном узле предварительное напряжение снижает нагрузку Q _x примерно на 3 %, а в нижнем, жестком, узле – на 5,3 %.

Заключение

Предварительные напряжения стальных стержней комбинированным способом позволяют снизить уровень моментов внешних нагрузок на 15 %, сгладить пиковые значения моментов, снизить нормальные напряжения и более рационально использовать прочностные характеристики материала стержней.

Результирующие прогибы предварительно напряженных стержней снижаются более чем на 40 %, что ведет к повышению изгибной жесткости исследуемых конструкций.

Снижение нормальных напряжений неизбежно сопровождается снижением массы конструкций и повышением их экономических показателей.

Повышение изгибной жесткости предварительно напряженных стержней позволяет рекомендовать их для колонн, находящихся преимущественно под воздействием изгибных напряжений, т.е. в колоннах каркасов зданий промышленного назначения, жестко закрепленных в фундаменте.